Scheitelpunktform
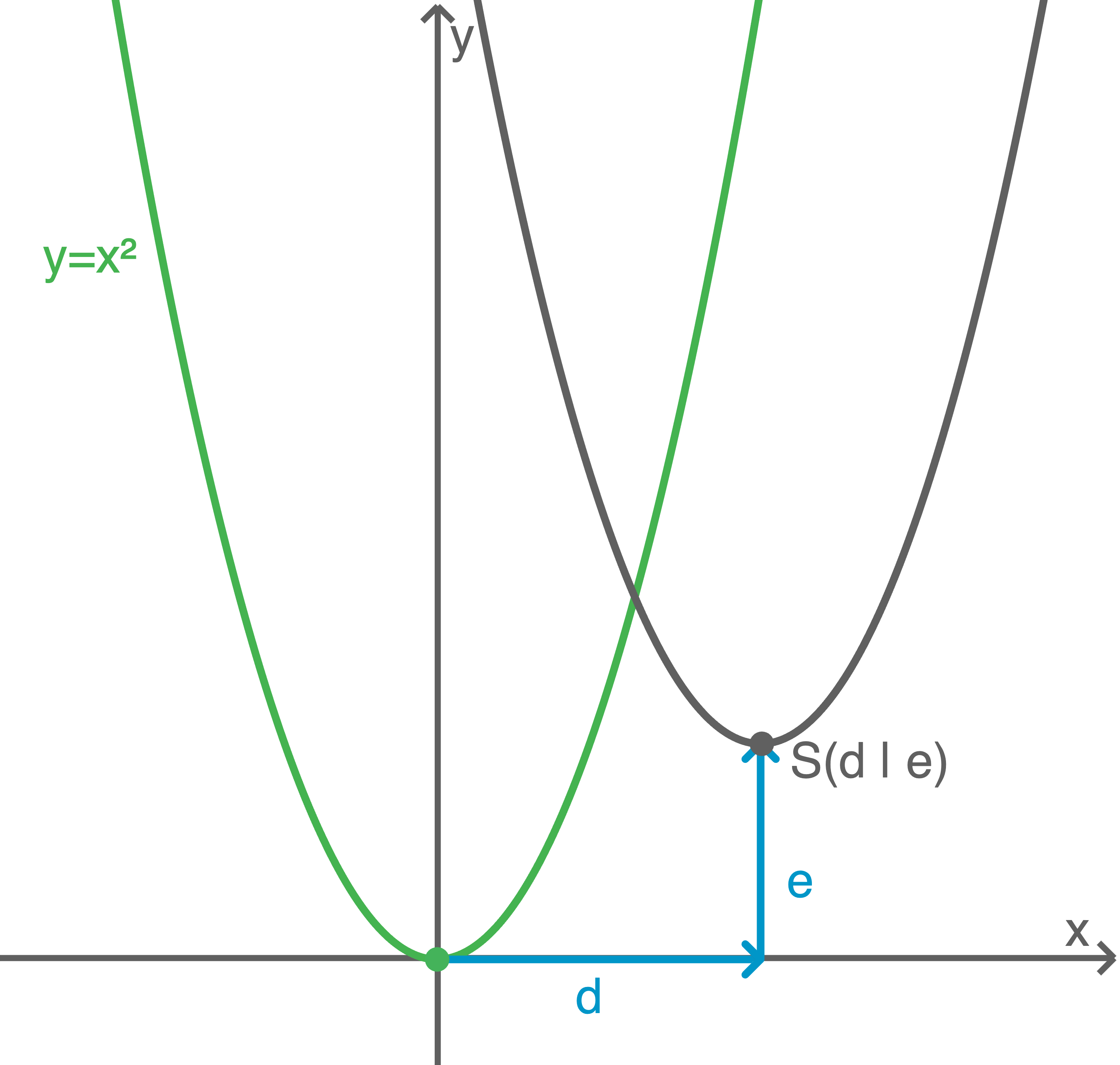
Funktionsgleichungen von verschobenen Parabeln der Form 
werden als Scheitelpunktform bezeichnet. Der Scheitelpunkt 
kann aus dieser direkt abgelesen werden.
Eine Streckung/ Stauchung durch den Faktor 
hat keinen Einfluss auf den Scheitelpunkt.
Die Graphen verschobener Parabeln können keinen, einen oder zwei Nullstellen haben.
werden als Scheitelpunktform bezeichnet. Der Scheitelpunkt kann aus dieser direkt abgelesen werden.
Eine Streckung/ Stauchung durch den Faktor hat keinen Einfluss auf den Scheitelpunkt.
Die Graphen verschobener Parabeln können keinen, einen oder zwei Nullstellen haben.
- Besitzt der Graph zwei Nullstellen, so ist der Mittelwert dieser der
-Wert des Scheitelpunkts. - Besitzt die Parabel eine Nullstelle, so entspricht diese dem -Wert des Scheitelpunkts.
1
Gib den Scheitelpunkt der Funktion an und überprüfe mit dem CAS.
a)
b)
c)
d)
2
Bestimme den Scheitelpunkt und die Funktionsgleichung der verschobenen Normalparabel.
a)
Die Normalparabel wurde um 2 LE nach links verschoben.
b)
Die Normalparabel wurde um 1 LE nach rechts verschoben.
c)
Die Normalparabel wurde um 3 LE nach rechts und um 1 LE nach oben verschoben.
d)
Die Normalparabel wurde um 2,5 LE nach links und um 3,5 LE nach unten verschoben.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
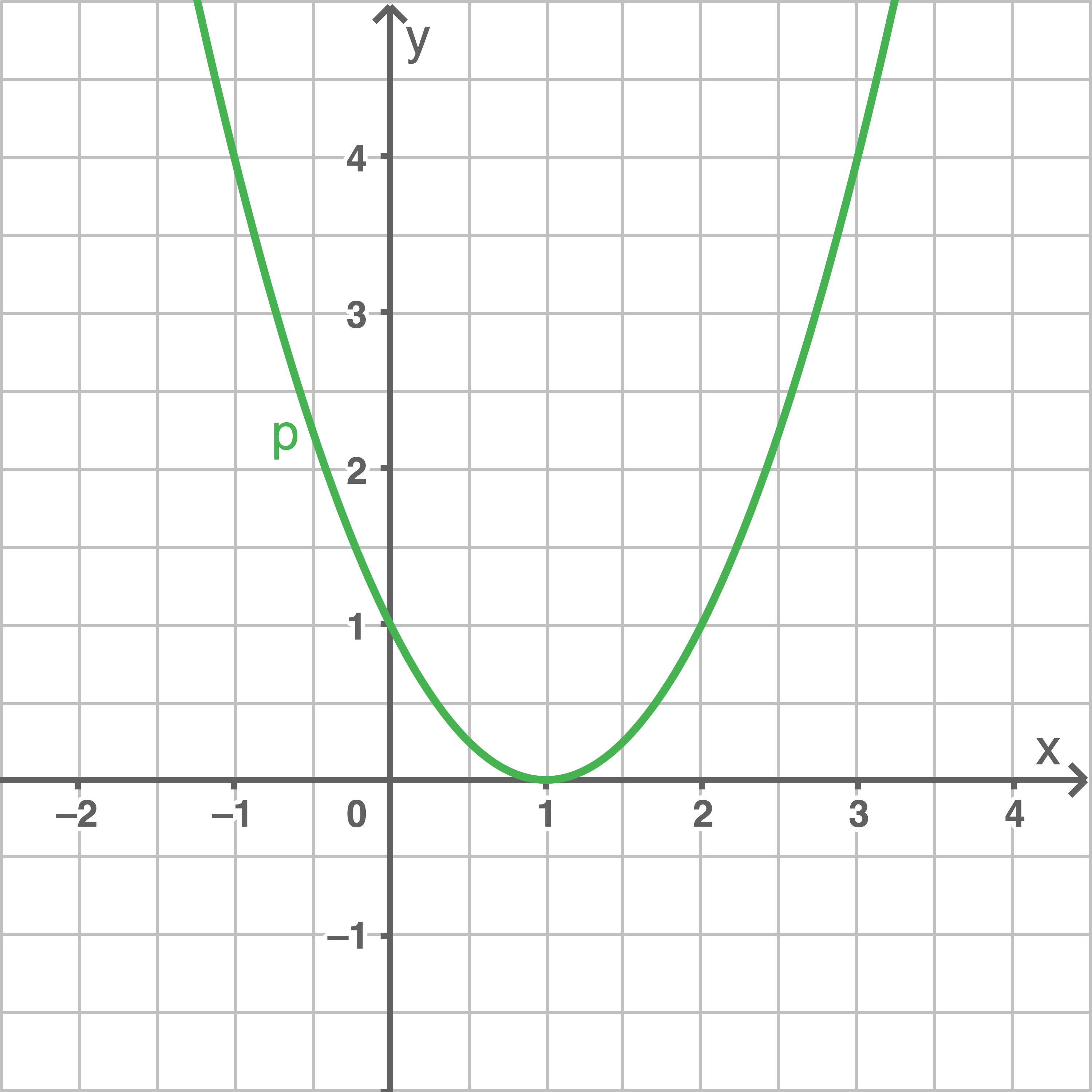
Mit 
und 
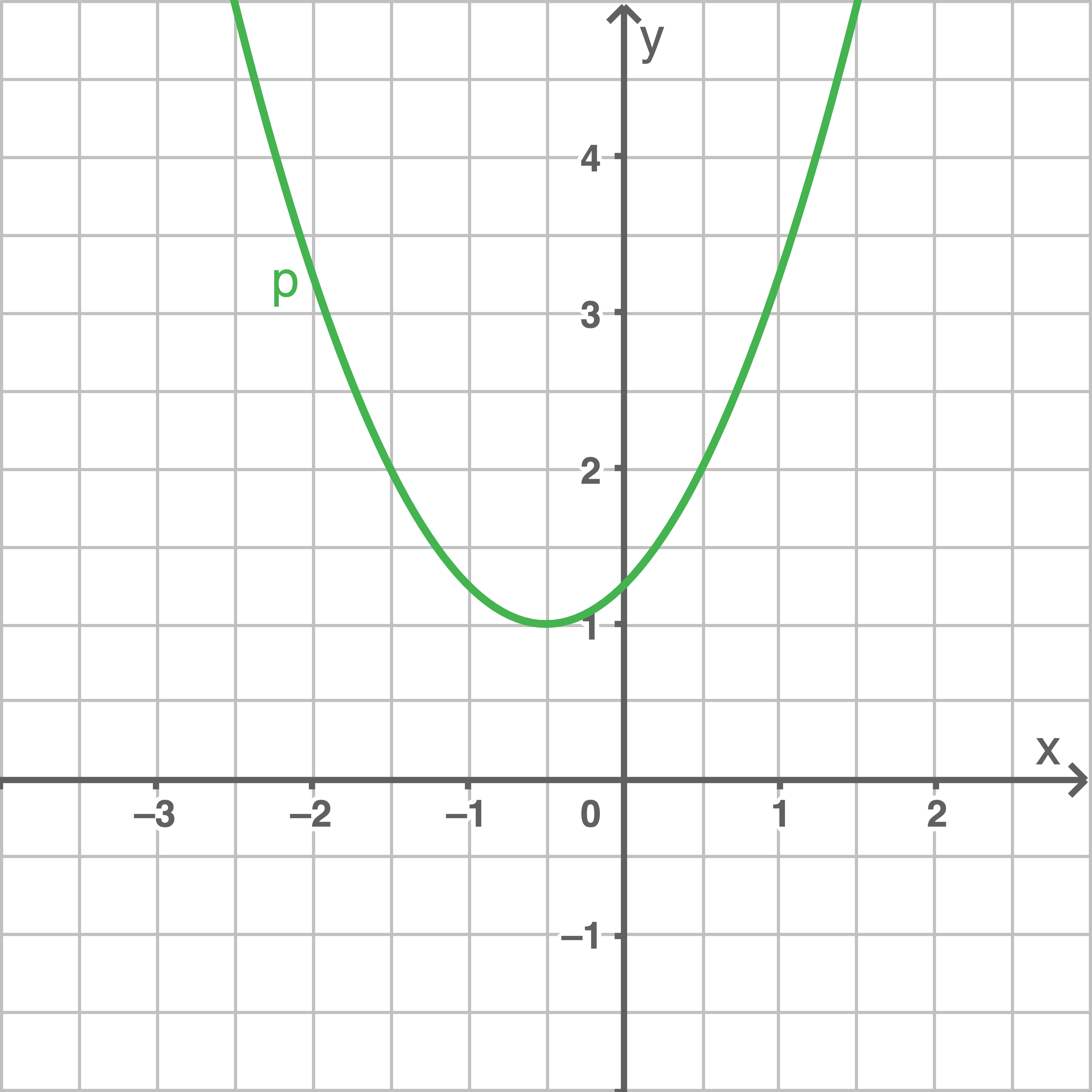
ergibt sich 
Der CAS liefert folgenden Graphen:
und ergibt sich
Der CAS liefert folgenden Graphen:
b)
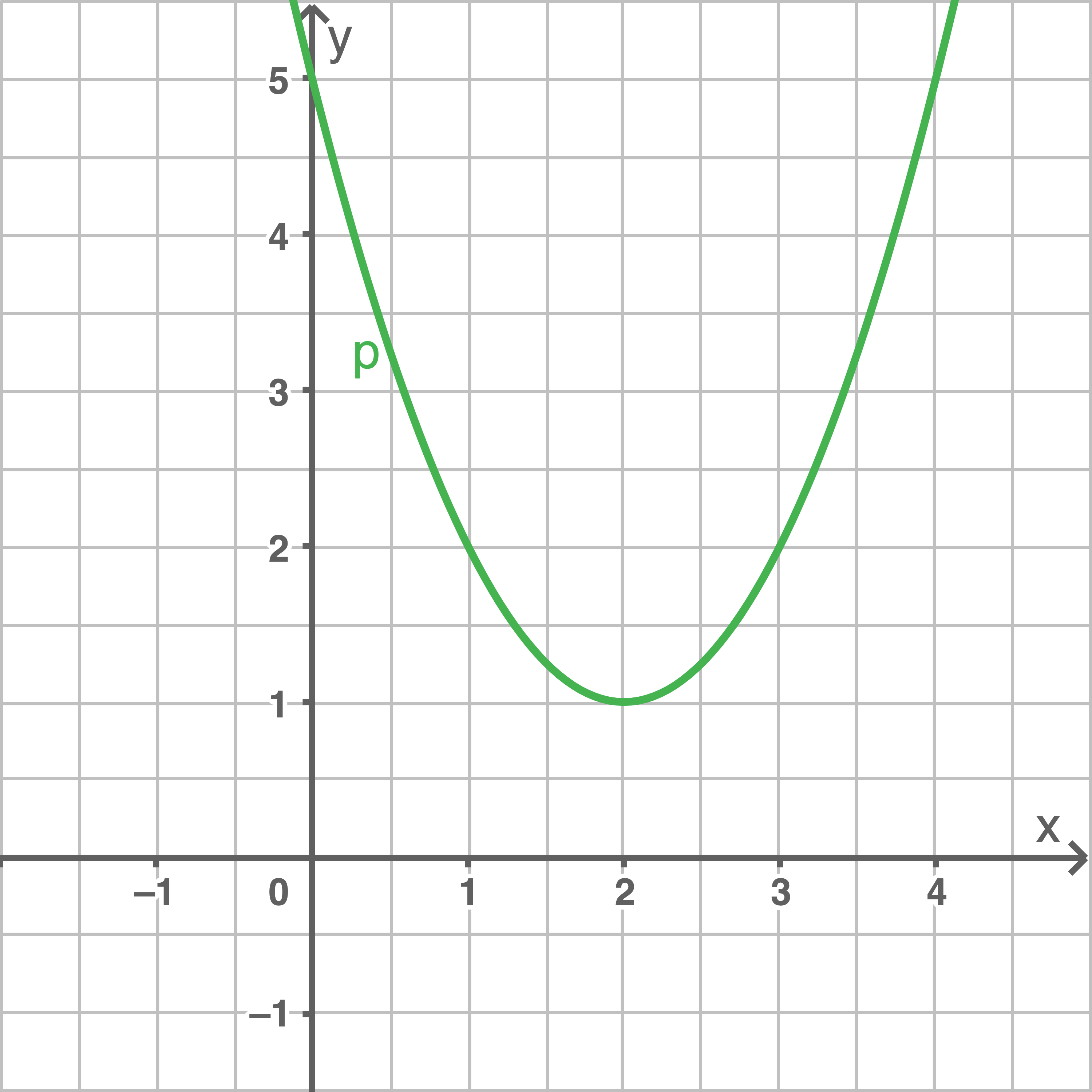
Mit 
und 
ergibt sich 
Der CAS liefert folgenden Graphen:
und ergibt sich
Der CAS liefert folgenden Graphen:
c)
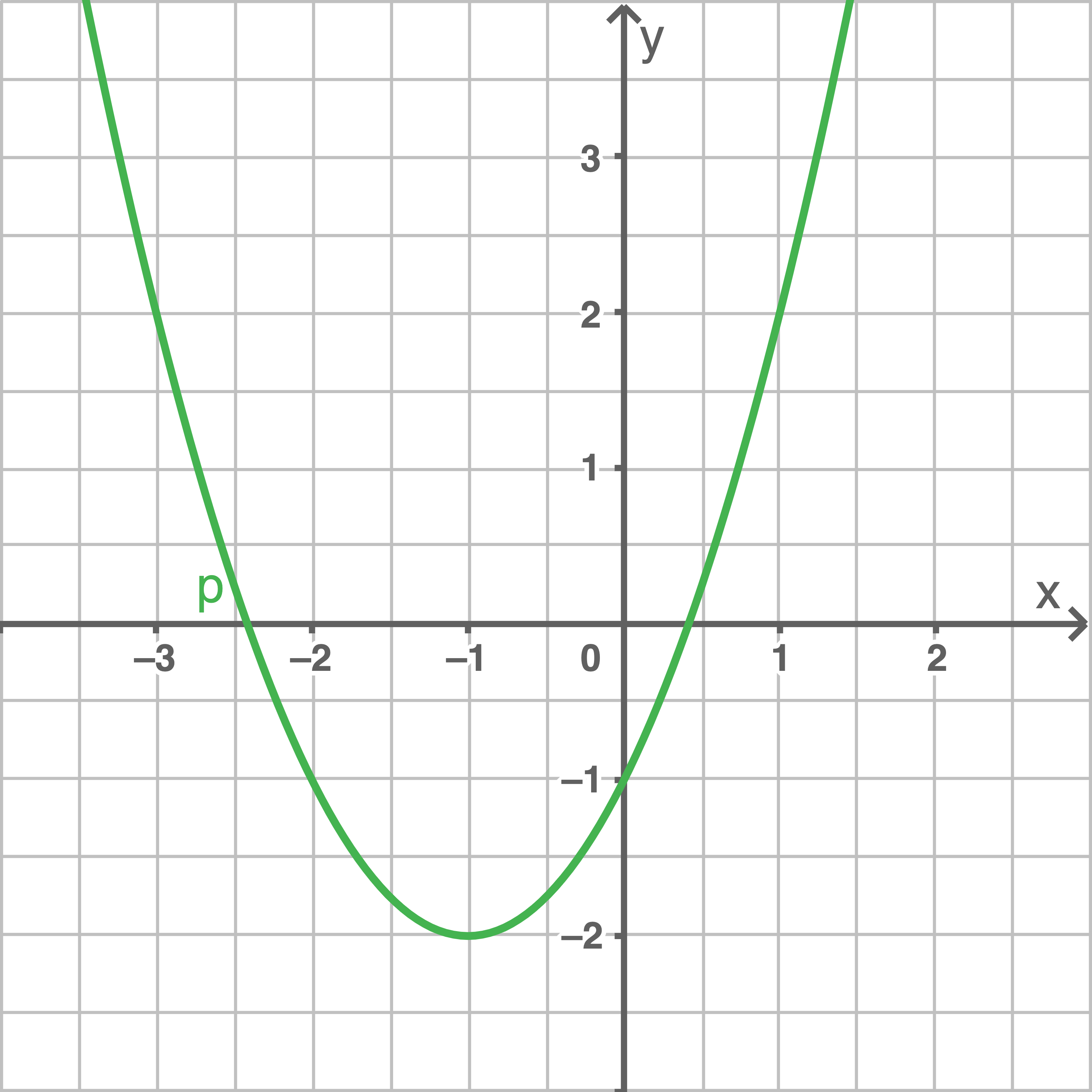
Mit 
und 
ergibt sich 
Der CAS liefert folgenden Graphen:
und ergibt sich
Der CAS liefert folgenden Graphen:
d)
Mit 
und ergibt sich 
Der CAS liefert folgenden Graphen:
und ergibt sich
Der CAS liefert folgenden Graphen:
2
a)
b)
c)
d)
