Streckung von Flächen
Definition
Wird ein Vieleck mit dem FlächeninhaltHerleitung
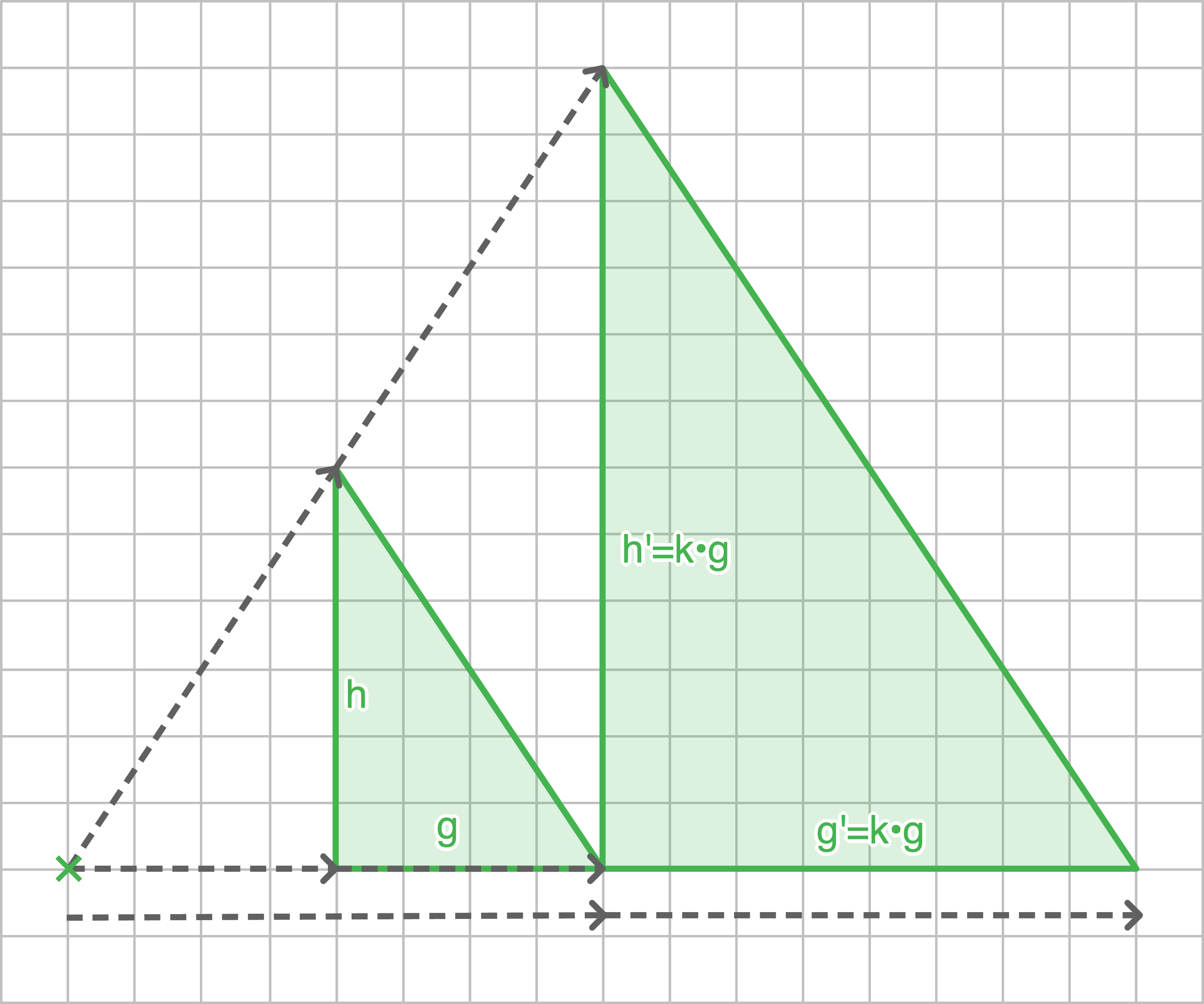
Herleitung durch Dreiecke
Wird ein Ausgangsdreieck mit der Grundseite 
der Höhe 
und folglich mit dem Flächeninhalt 
mit dem Faktor 
gestreckt, so gilt für das neue Dreieck nach der zentrischen Streckung:
des gestreckten Dreiecks folgt also:
![\(\begin{array}[t]{rlll}
A](https://mathjax.schullv.de/811aedaf6c8cfd228efd4cb0b3156ec01c67c8cc37d8d9a0b3da00b35e610827?color=5a5a5a)
- Grundseite:
- Höhe:
Übertragung auf Vielecke
Da sich jedes beliebige Vieleck in Dreiecke zerlegen lässt, deren Flächeninhalte sich jeweils um den Faktor 
verändern, gilt diese Regel auch für die Summe der Dreiecksflächen und somit für das gesamte Vieleck.
Beispiel
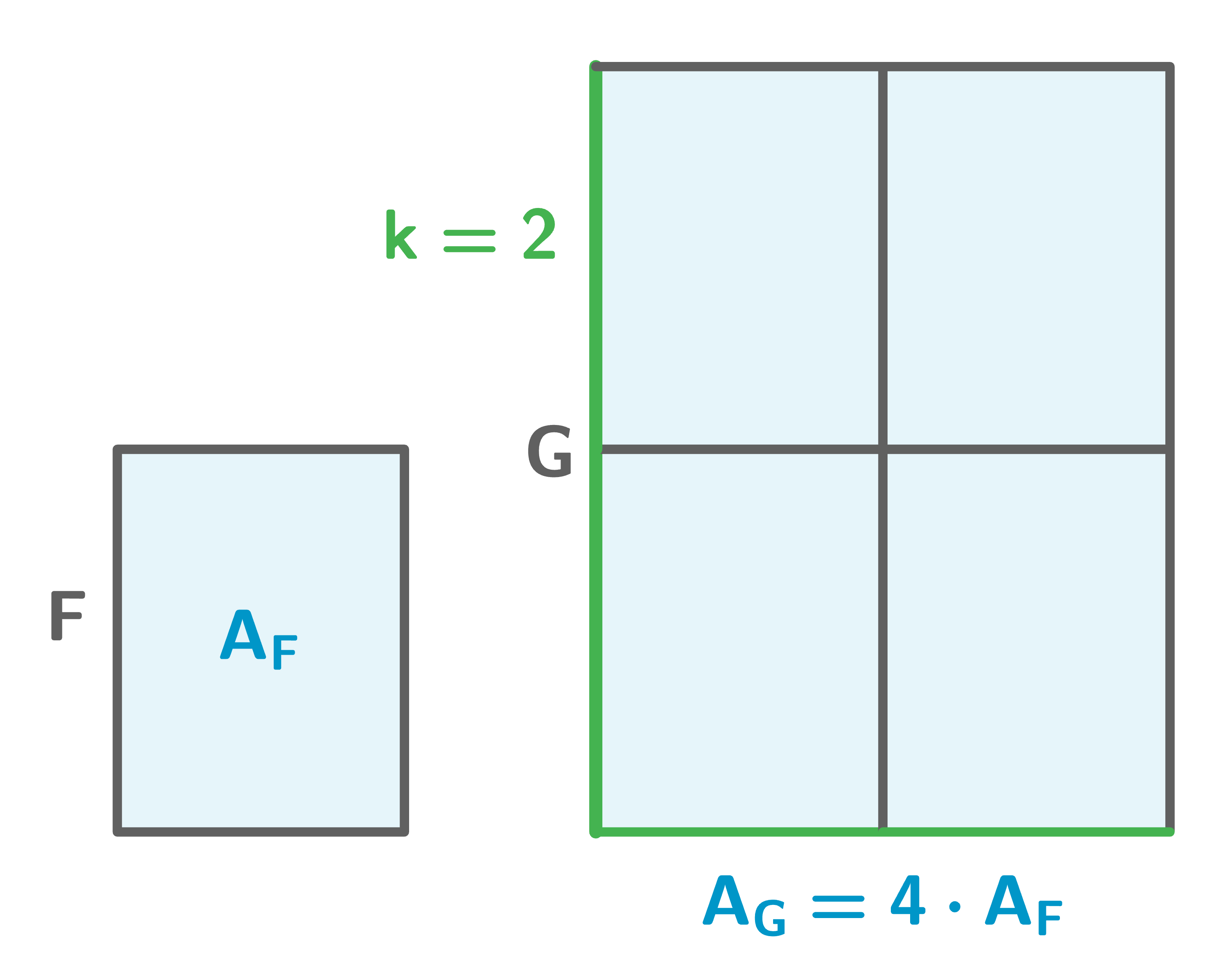
Die Vielecke 
und 
sind ähnlich zueinander.
ist aus durch Vergrößerung mit dem Längenverhältnis 
entstanden. Für den Flächeninhalt gilt dann:
![\(\begin{array}[t]{rlll}
A_G&=& k^2\cdot A_F & \\[5pt]
&=& 2^2\cdot A_F & \\[5pt]
&=& 4 \cdot A_F
\end{array}\)](https://mathjax.schullv.de/8055fa960fe0ea6f0a80030044de25894f4ee69694d05ddd0ad4d9cc79bdc99b?color=5a5a5a)
1
Das Rechteck 
hat den Flächeninhalt 
Ein dazu ähnliches Rechteck 
entsteht durch Streckung des Rechtecks mit dem Streckungsfaktor 
Berechne den Flächeninhalt des Rechtecks 
a)
c)
b)
d)
2
Aus dem Rechteck mit den Seitenlängen 
und 
entsteht das Rechteck mit dem jeweiligen Streckungsfaktor
Berechne jeweils den Umfang und den Flächeninhalt des Rechtecks
Berechne jeweils den Umfang und den Flächeninhalt des Rechtecks
a)
c)
b)
d)
3
Das Quadrat hat den Flächeninhalt 
Ein dazu ähnliches Quadrat hat den angegebenen Flächeninhalt.
Berechne den Streckungsfaktor
a)
c)
b)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
c)
b)
d)
2
a)
c)
b)
d)
3
a)
Es gilt:
![\(\begin{array}[t]{rlll}
A_{A](https://mathjax.schullv.de/5f0fe2f31cfab9b127a33eac33ac16013ddf49e527593842679e99c771f46394?color=5a5a5a)
Für 
folgt also:
b)
Für 
gilt:
c)
Für 
gilt:
d)
Für 
gilt:
