Quadratische Gleichungen anwenden
Vorgehen
Modellieren von Problemen mit quadratischen Gleichungen
- Sachverhalt vereinfacht darstellen, z.B. mithilfe einer Skizze
- Variablen für gesuchte Größe einführen
- Quadratische Gleichung aufstellen
- Geeignete Lösungsmethode anwenden
- Lösungen im Sachzusammenhang prüfen
- Ergebnis angeben
Beispiel
Ein rechteckiges Grundstück ist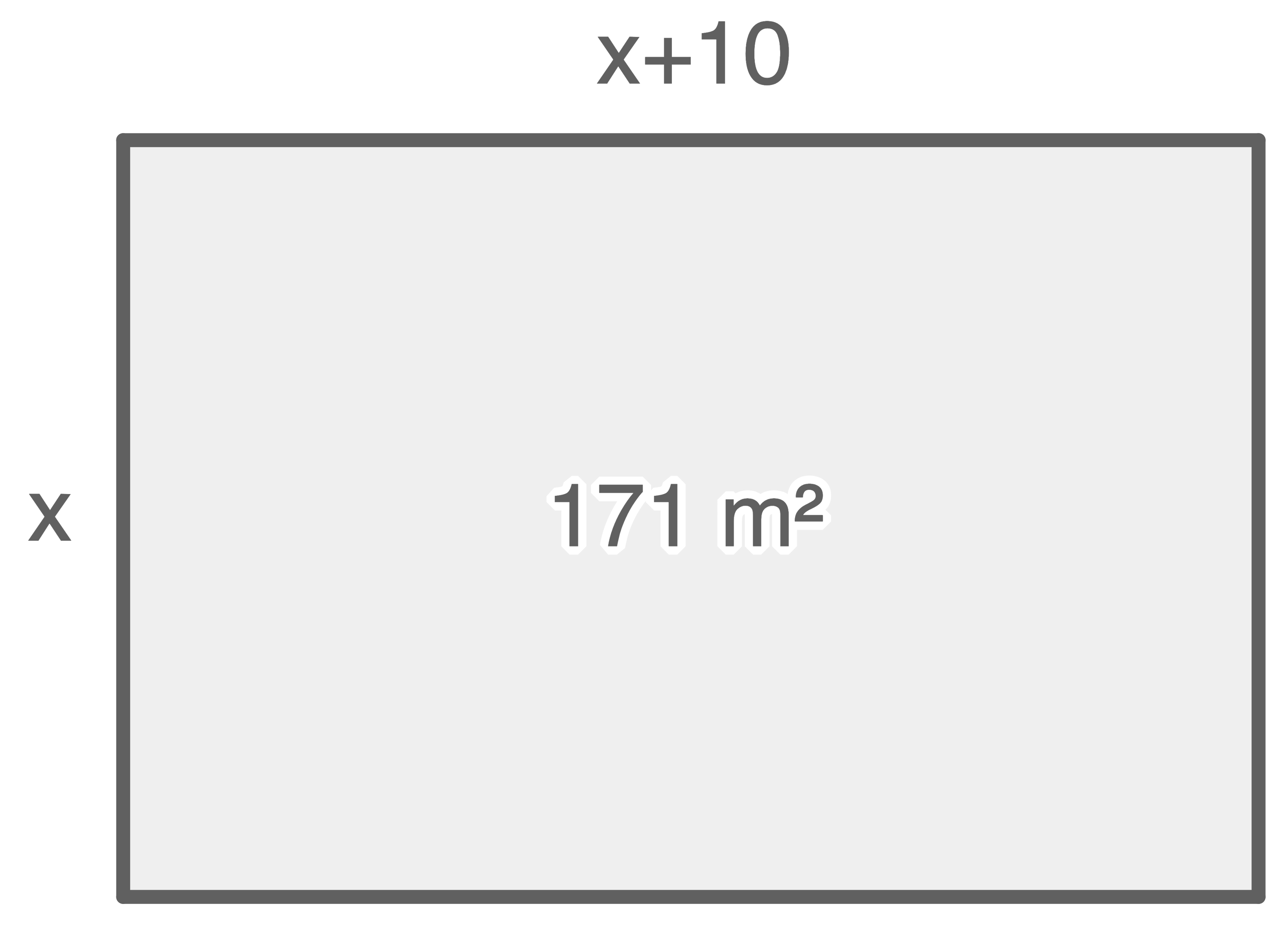
Breite:
1
Verlängert man alle Seitenlängen eines Würfels um 
so nimmt sein Volumen um 
zu.
Wie lang ist die ursprüngliche Seitenlänge des Würfels?
2
Ein Bild der Größe 
soll in einen Holzrahmen eingerahmt werden, der überall die gleiche Breite hat. Die Fläche des Rahmens soll halb so groß sein wie die Fläche des Bildes.
Welche Breite hat der Rahmen?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1. Schritt: Sachverhalt darstellen
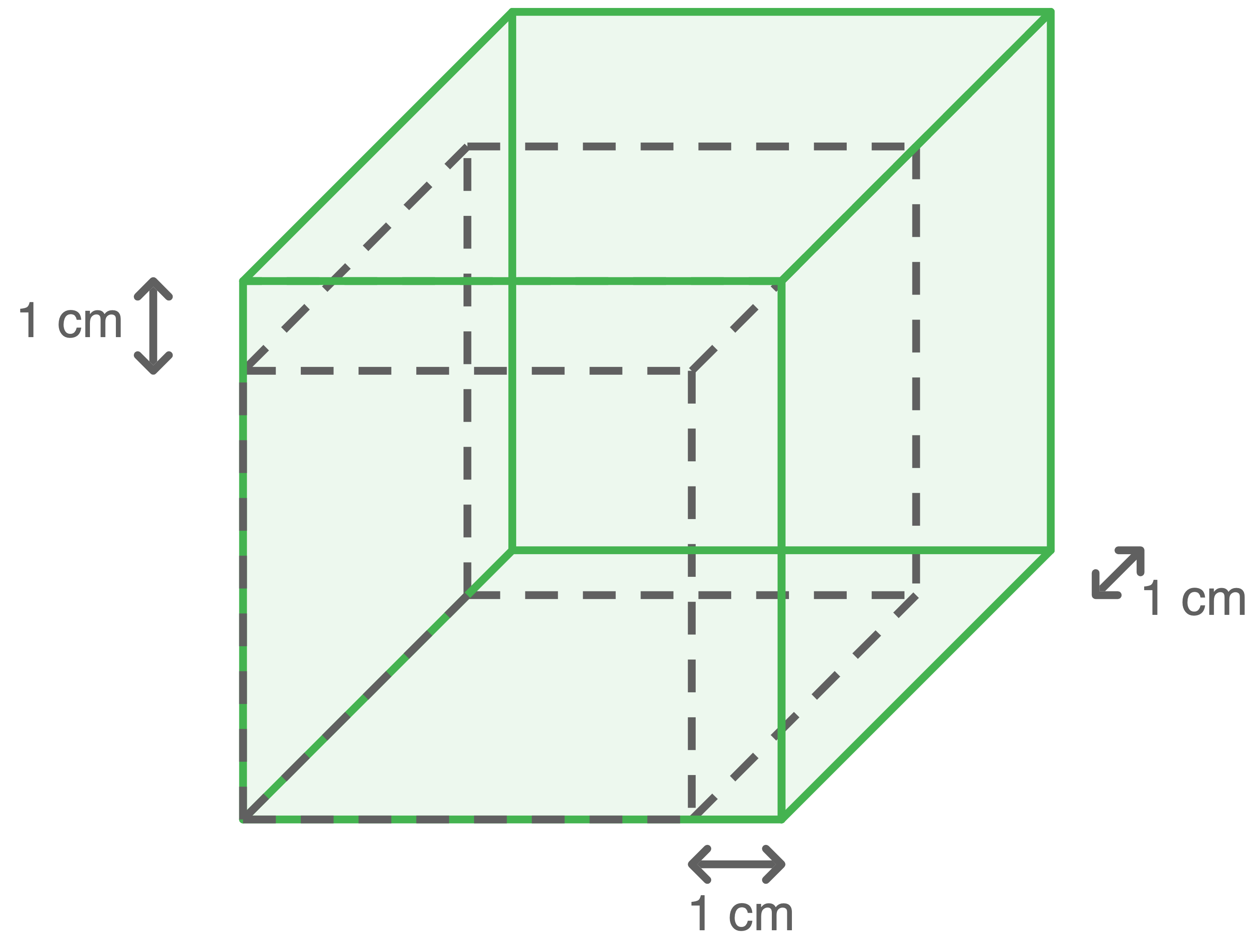2. Schritt: Variablen einführen
Ursprüngliche Seitenlänge
3. Schritt: Quadratische Gleichung aufstellen
![\(\begin{array}[t]{rll}
(x+1)^3-x^3&=& 127 \\[5pt]
x^3+3x^2+3x+1-x^3&=& 127 \\[5pt]
3x^2+3x+1&=& 127 \quad \scriptsize \mid\; -127 \\[5pt]
3x^2+3x-126&=& 0 \quad \scriptsize \mid\; :3 \\[5pt]
x^2+x-42&=& 0
\end{array}\)](https://mathjax.schullv.de/c417835f6ff105655edbbe8dbfb0712e10b92e437c100f39b433bf9cdd339b73?color=5a5a5a)
4. Schritt: Lösungsmethode wählen
Mit der 
-Formel ergibt sich:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{1}{2}\pm \sqrt{\left(\dfrac{1}{2}\right)^2-(-42)} \\[5pt]
&=& -\dfrac{1}{2}\pm 6,5 \\[5pt]
x_1&=& 6 \\[5pt]
x_2&=& -7
\end{array}\)](https://mathjax.schullv.de/af0fdbbeeb9b1e9d1c2f085a9cf5e6d21575a53ca6e8ead1b4b17b750483a011?color=5a5a5a)
5. Schritt: Ergebnis im Sachzusammenhang prüfen
Die Lösung 
entfällt im Sachzusammenhang, da die Kantenlänge des Würfels nicht negativ sein kann.
6. Schritt: Ergebnis angeben
Die ursprüngliche Kantenlänge des Würfels beträgt 
2
1. Schritt: Sachverhalt darstellen
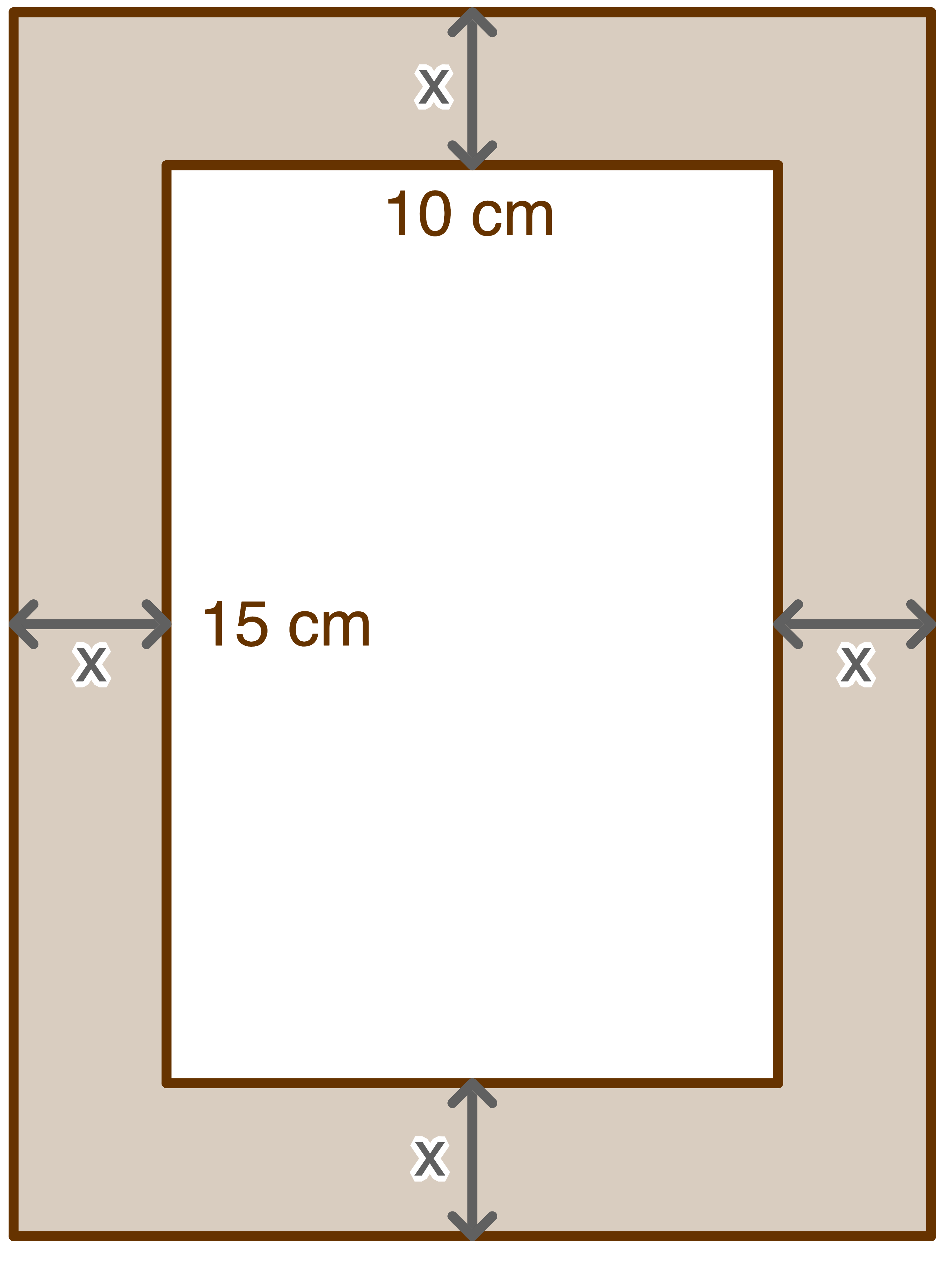2. Schritt: Variablen einführen
Breite des Rahmens
3. Schritt: Quadratische Gleichung aufstellen
Flächeninhalt des Bildes:
Somit muss gelten:
![\(\begin{array}[t]{rll}
(2x+10)\cdot (2x+15)-150&=& \dfrac{1}{2}\cdot 150 \\[5pt]
4x^2+30x+20x+150-150&=& 75 \\[5pt]
4x^2+50x&=& 75 \quad \scriptsize \mid\; -75 \\[5pt]
4x^2+50x-75&=& 0 \quad \scriptsize \mid\; :4 \\[5pt]
x^2+12,5x-18,75&=& 0
\end{array}\)](https://mathjax.schullv.de/3b8e655dac1a4920a5b376d0e9daa589319dea5a20a98882dc452727578d83cf?color=5a5a5a)
4. Schritt: Lösungsmethode wählen
Mit der -Formel ergibt sich:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{12,5}{2}\pm \sqrt{\left(\dfrac{12,5}{2}\right)^2-(-18,5)} \\[5pt]
&\approx& -6,25\pm 7,6 \\[5pt]
x_1&\approx& 1,35 \\[5pt]
x_2&\approx& -13,85
\end{array}\)](https://mathjax.schullv.de/90ca4bf0c675790158c6a74c1dd67cf9efaa533f00692b6c17b47d0034051766?color=5a5a5a)
5. Schritt: Ergebnis im Sachzusammenhang prüfen
Die Lösung 
entfällt im Sachzusammenhang, da die Breite des Rahmens nicht negativ sein kann.
6. Schritt: Ergebnis angeben
Der Rahmen ist ungefähr 
breit.