Strahlensätze
Definition
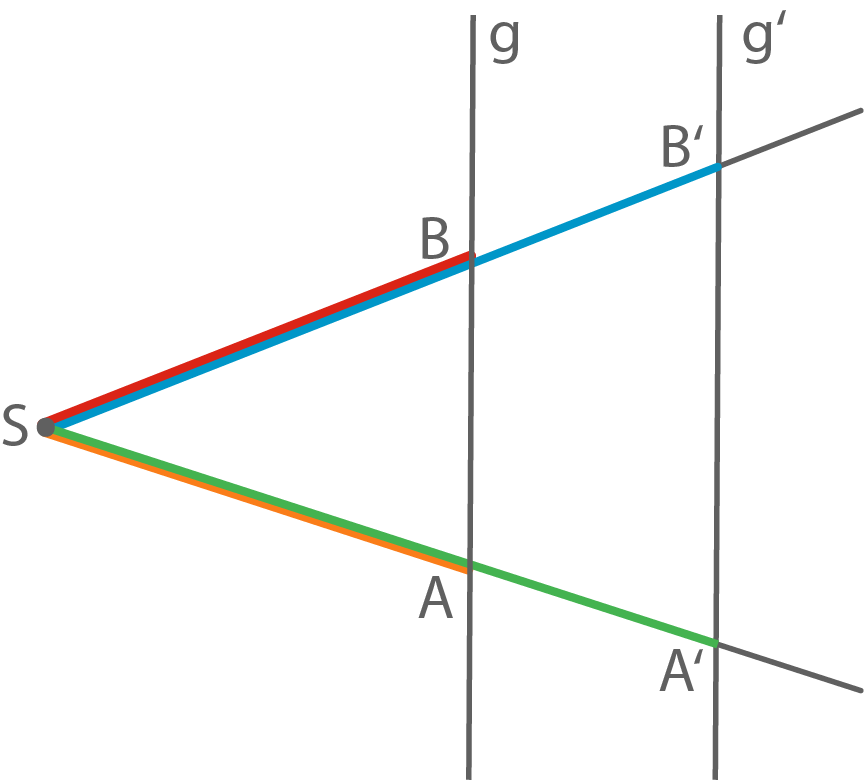
Für eine Figur gelten die Strahlensätze, wenn zwei Strahlen – gerade Linien, die auf einer Seite begrenzt sind, sich aber auf der anderen Seite ins Unendliche erstrecken – mit gemeinsamem AnfangspunktErster Strahlensatz
Bei einer Strahlensatzfigur gilt: Die Längenverhältnisse der Abschnitte sind auf den beiden Strahlen gleich.
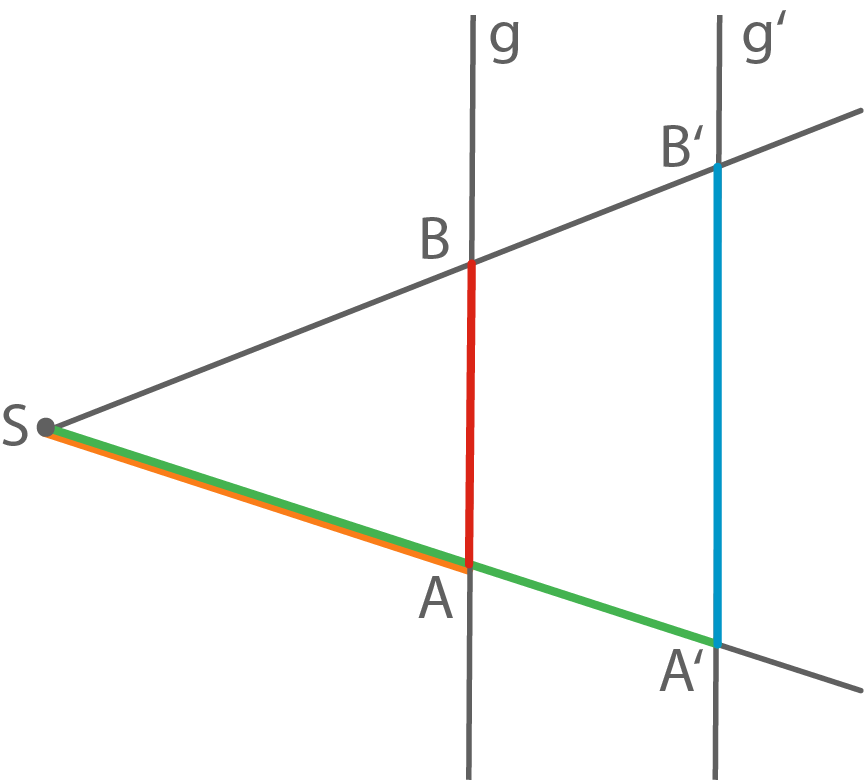
Zweiter Strahlensatz
Bei einer Strahlensatzfigur gilt außerdem: Das Längenverhältnis der parallelen Strecken ist gleich dem Längenverhältnis der Abschnitte auf den Strahlen.
und 
Umkehrbarkeit
Ein mathematischer Satz ist umkehrbar, wenn nicht nur aus seinen Voraussetzungen auf das Ergebnis, sondern auch aus dem Ergebnis wieder auf die Voraussetzungen geschlossen werden kann. Der erste Strahlensatz ist umkehrbar: Werden zwei Strahlen mit gemeinsamem Anfangspunkt von zwei Geraden geschnitten und ist das Längenverhältnis der Abschnitte auf den beiden Strahlen gleich, so sind die beiden Geraden parallel. Der zweite Strahlensatz ist nicht umkehrbar: Aus den entsprechenden Längenverhältnissen folgt nicht direkt, dass die beiden Geraden parallel sind.Erweiterung der Strahlensätze
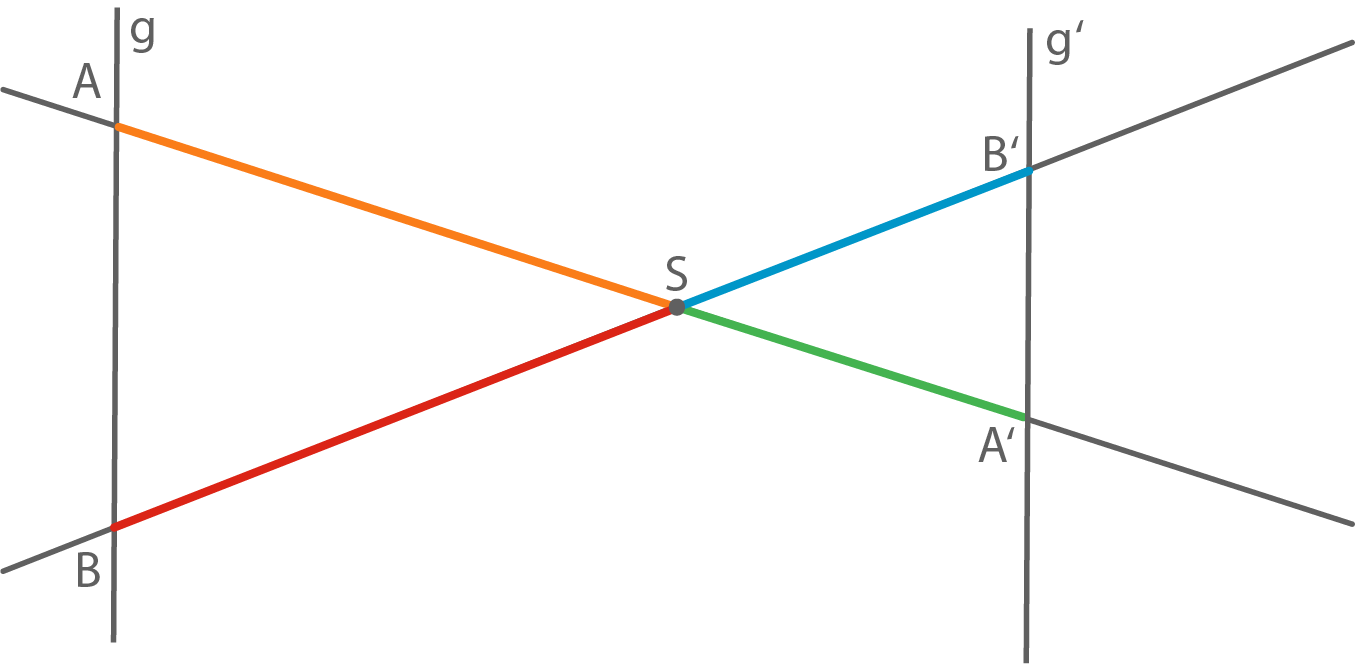
Die Strahlensätze gelten auch, wenn
1. Strahlensatz:
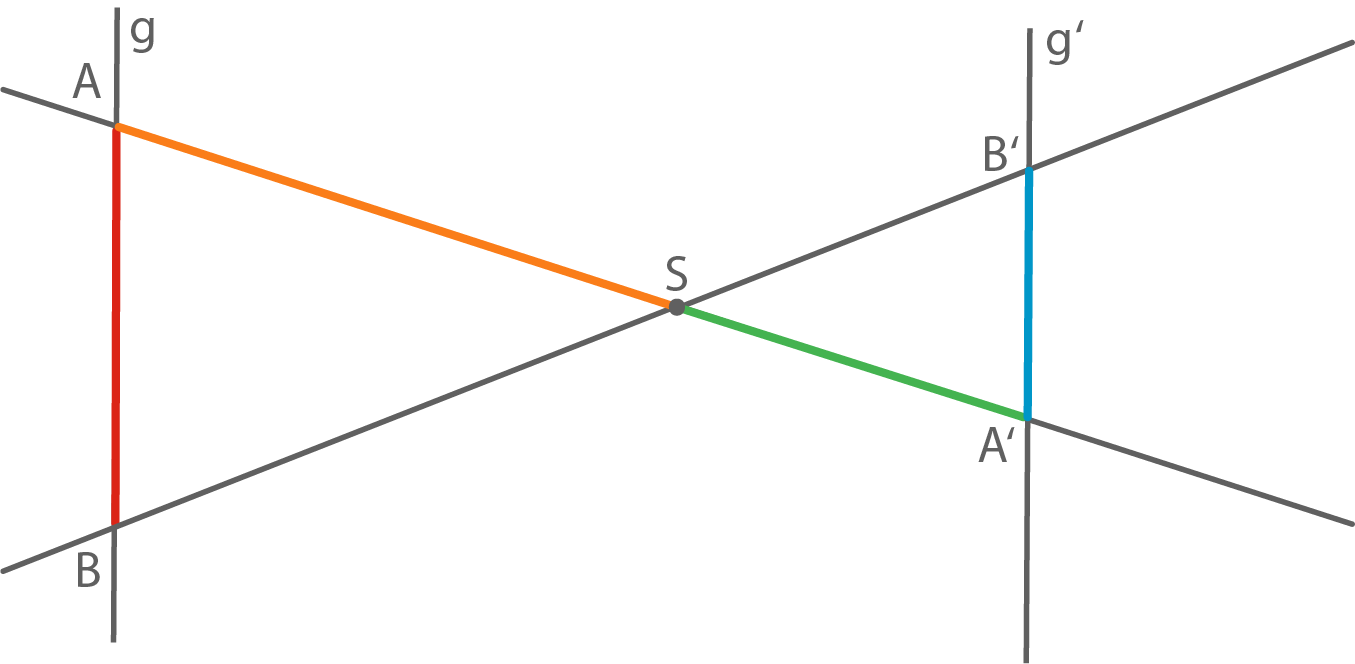
2. Strahlensatz:
und
1.
Die Geraden ist 
und 
sind parallel zueinander.
Berechne die fehlenden Längen.
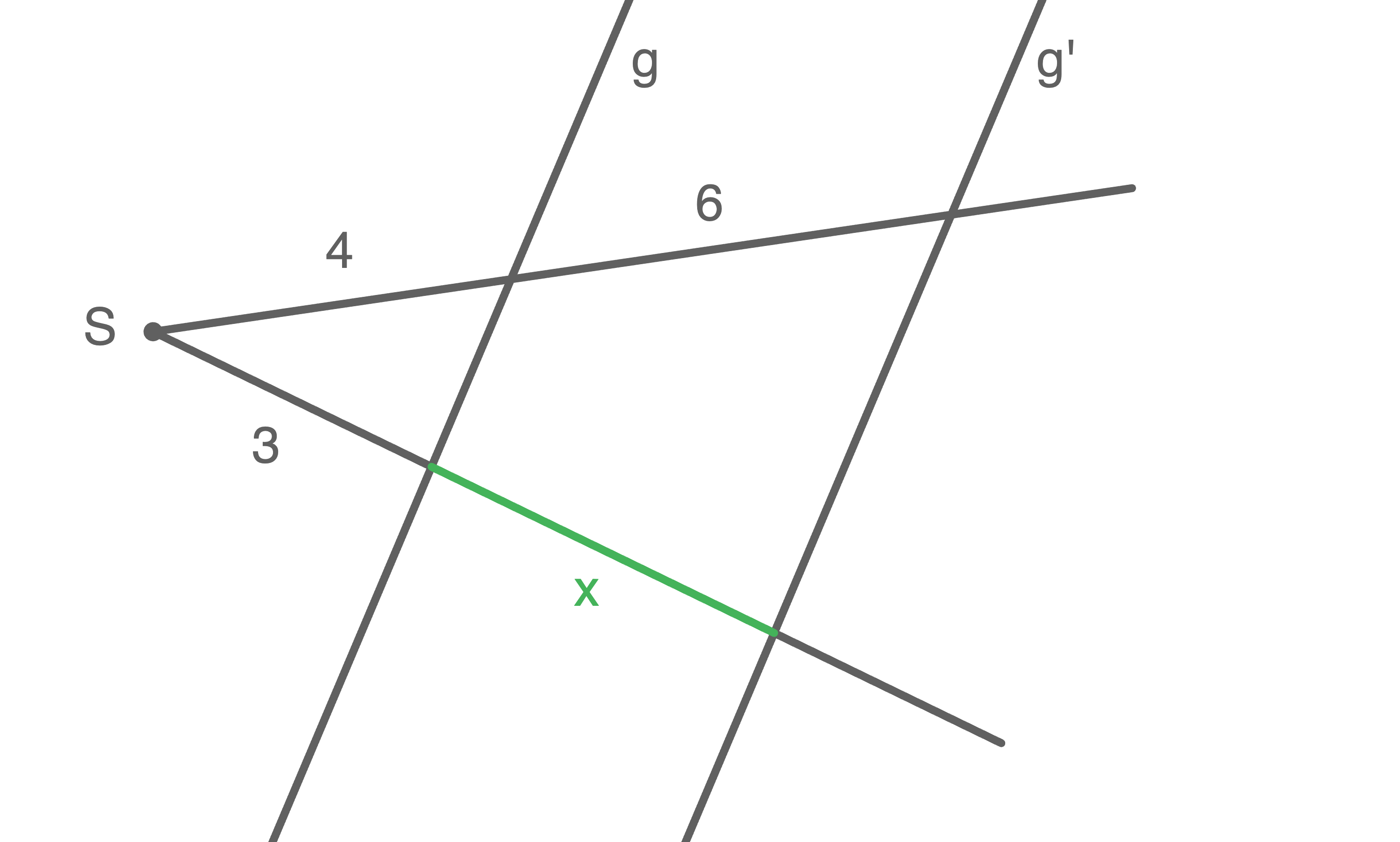
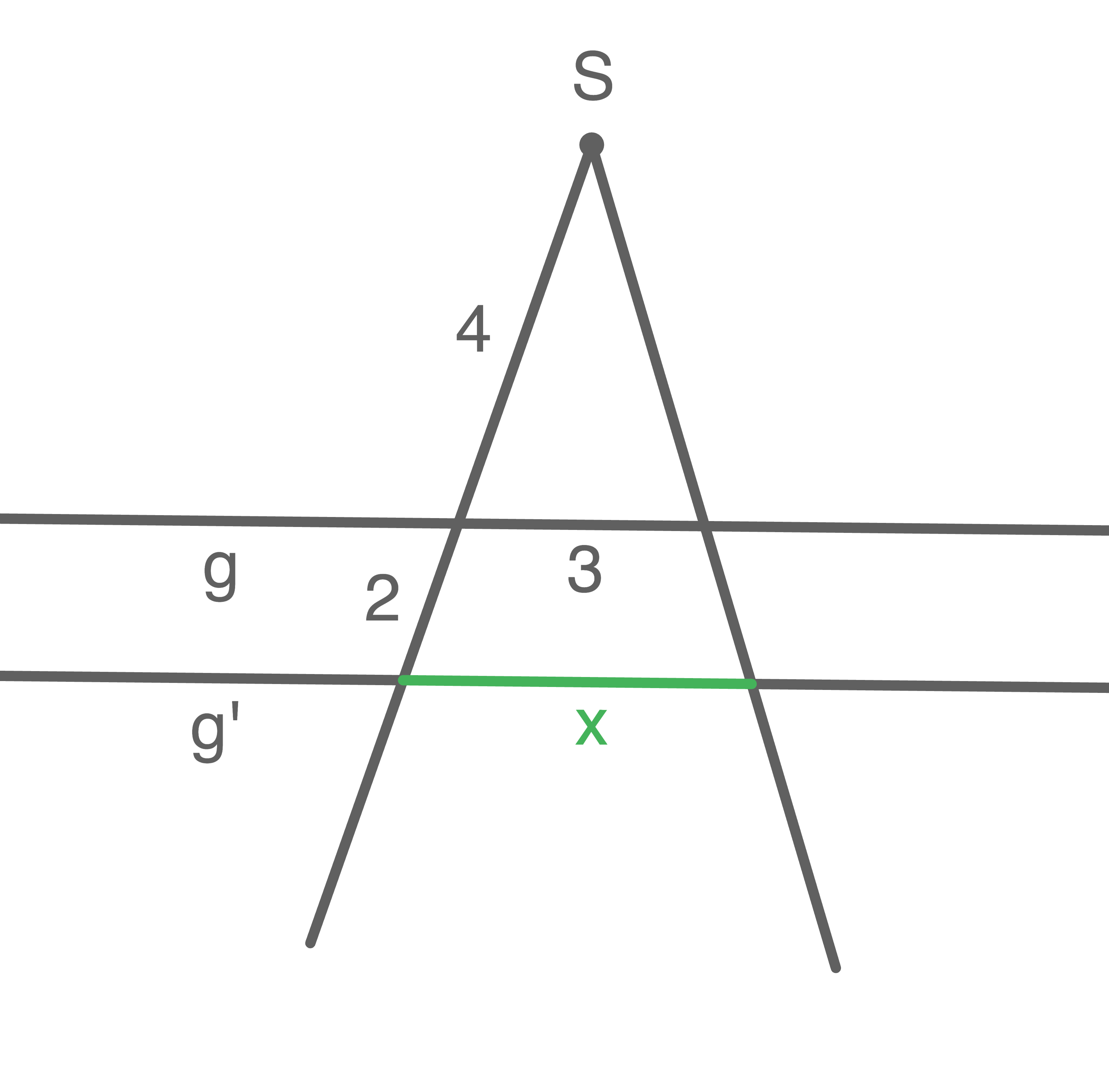
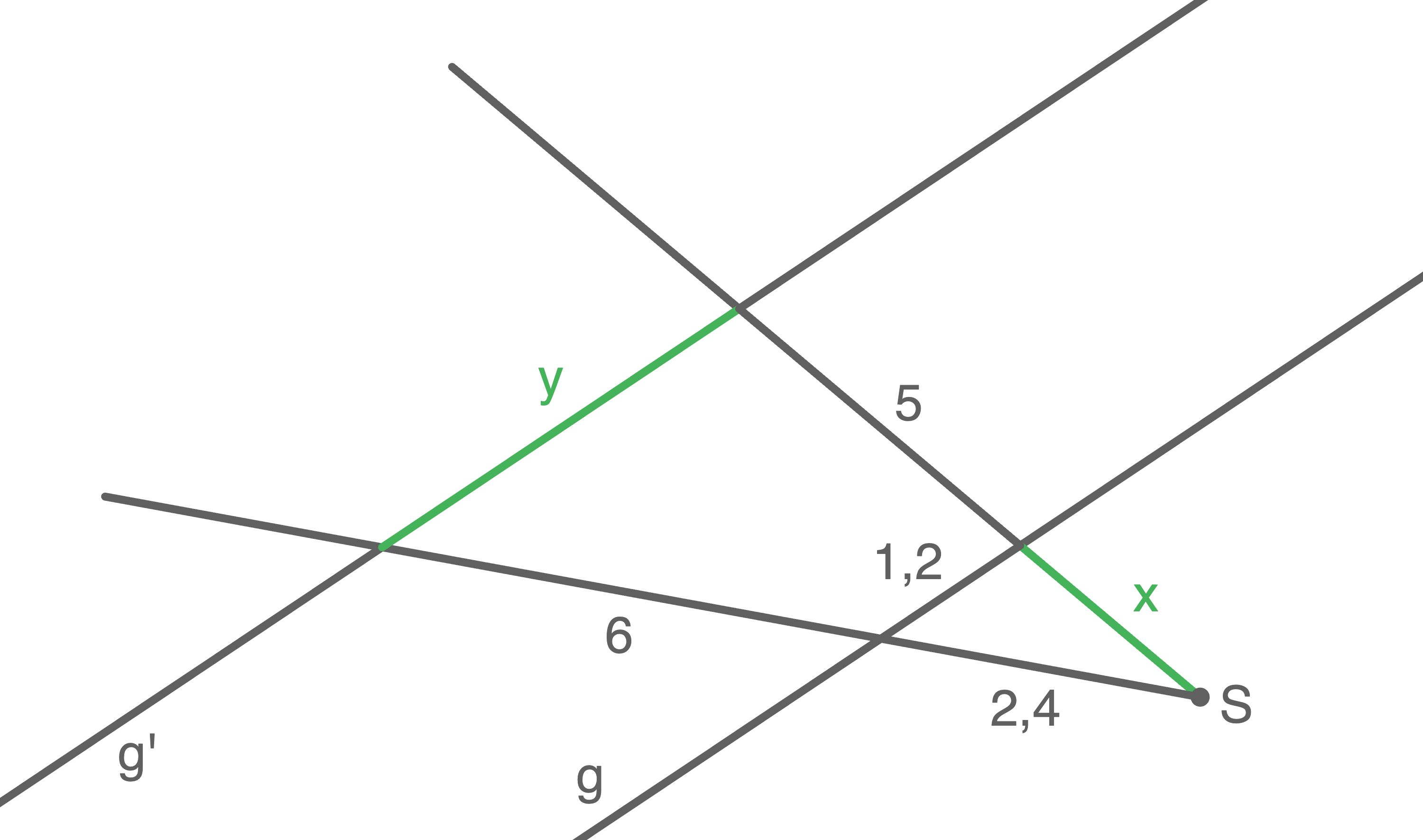
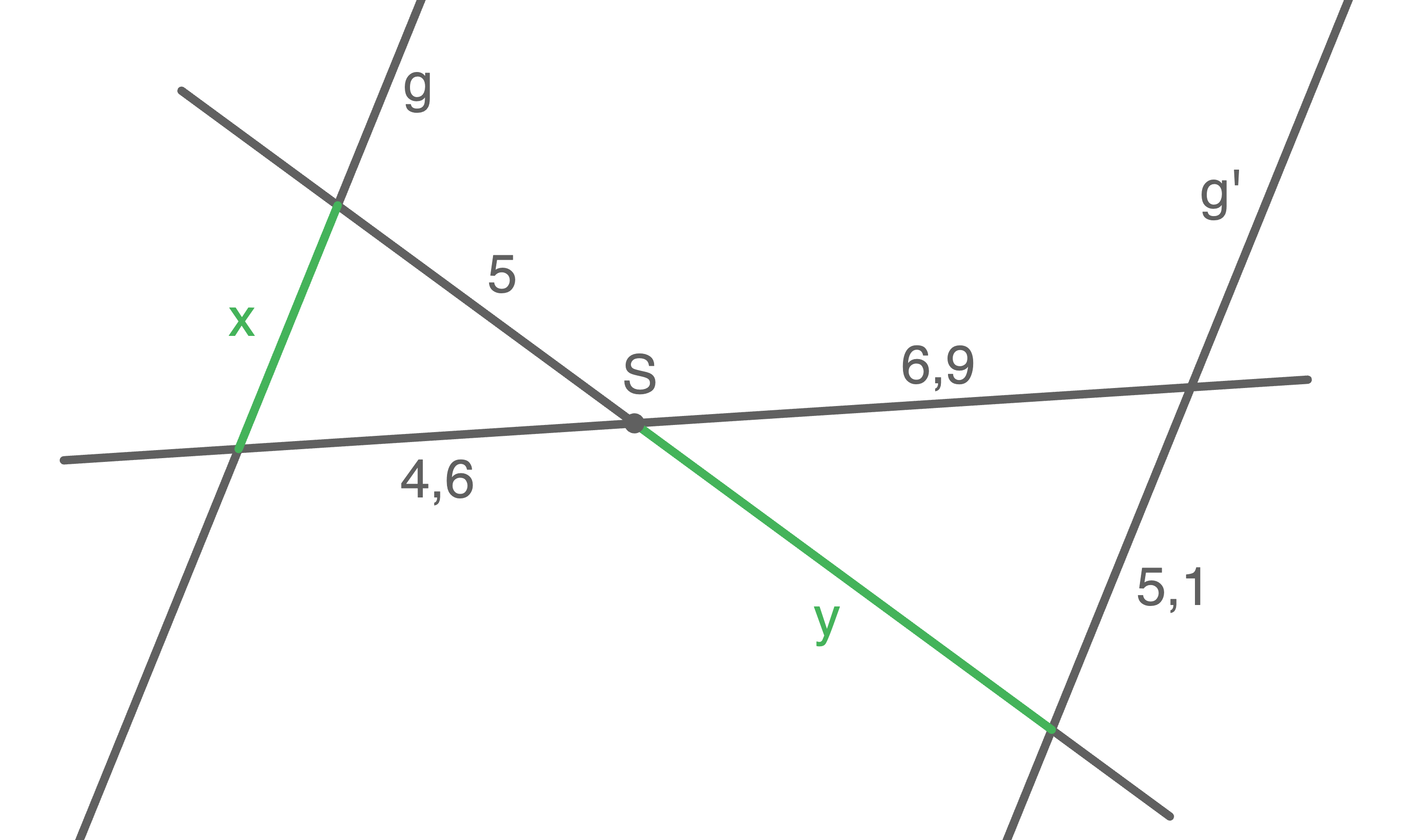
a)
b)
c)
d)
2
Mira will die Höhe des Eiffelturms bestimmen. Dazu misst sie den Schatten des Eiffelturms, welcher 
beträgt. Sie selbst ist 
groß und stellt sich so hin, dass ihr Schatten genau mit dem Schattenende des Eiffelturms zusammenfällt. Mira selbst steht so nun 
vom Eiffelturm entfernt.
Wie hoch ist der Eiffelturm?
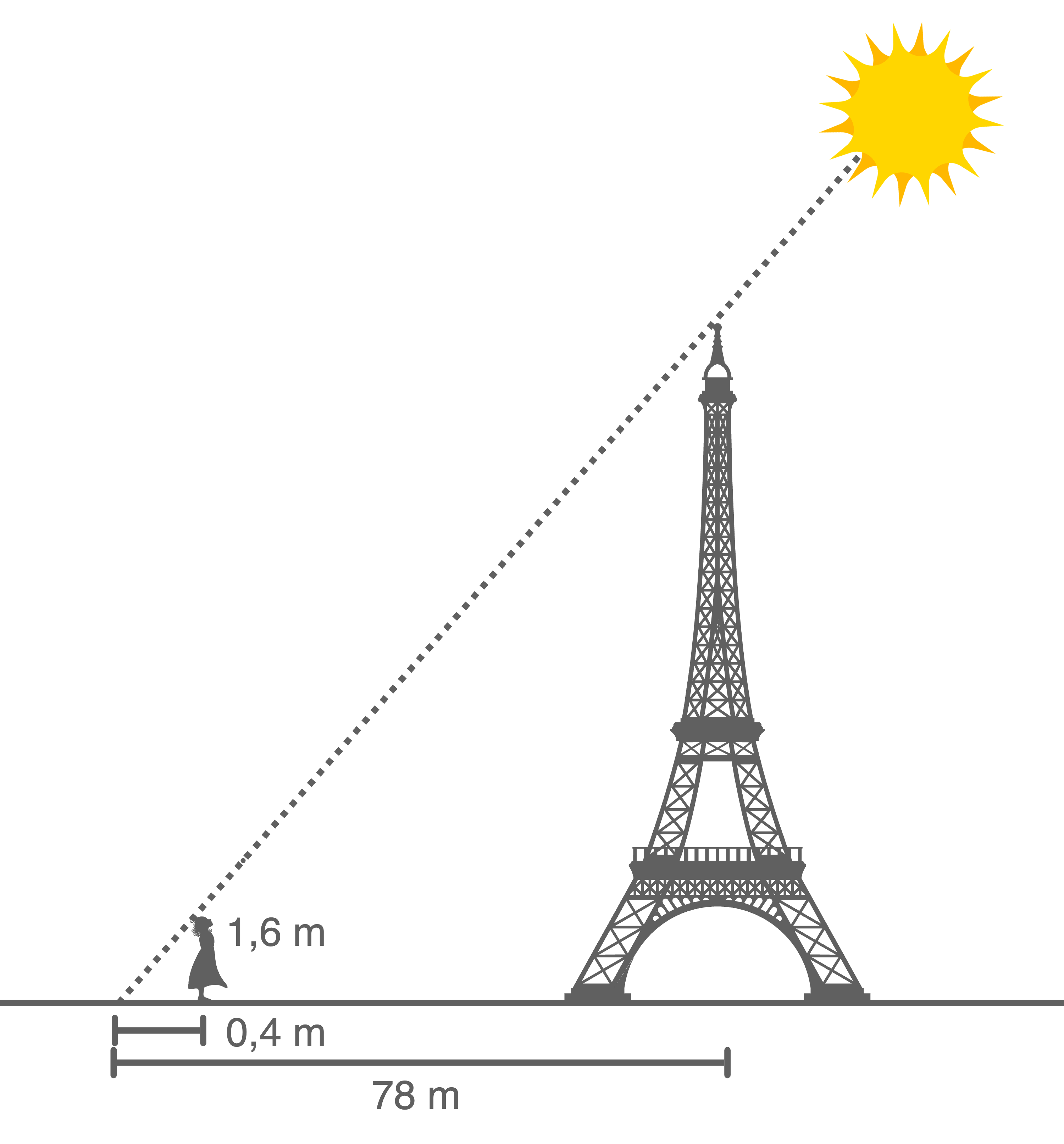
(nicht maßstäblich)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Mit dem ersten Strahlensatz gilt:
![\(\begin{array}[t]{rlll}
\dfrac{10}{4}&=& \dfrac{3+x}{3} &\mid\; \cdot 3 \\[5pt]
2,5\cdot 3&=& 3+x &\mid\; \cdot (-3) \\[5pt]
4,5 &=& x
\end{array}\)](https://mathjax.schullv.de/2da2c1a7bfb0885ae68ba2841e2847fe21038e6e00a0334b30a926e6e5bce0f1?color=5a5a5a)
b)
Mit dem zweiten Strahlensatz gilt:
![\(\begin{array}[t]{rlll}
\dfrac{x}{3}&=& \dfrac{6}{4} &\mid\;\cdot 3 \\[5pt]
x&=& 1,5\cdot 3x & \\[5pt]
x&=& 4,5
\end{array}\)](https://mathjax.schullv.de/0af2a0262a7ed0cb4d3cbc1918da15562c614fa479b308fe240b95fbb090a972?color=5a5a5a)
c)
Mit dem ersten Strahlensatz gilt:
![\(\begin{array}[t]{rlll}
\dfrac{8,4}{2,4}&=& \dfrac{5+x}{x}&\mid\; \cdot x \\[5pt]
3,5\cdot x&=& 5+x &\mid\; -x\\[5pt]
2,5\cdot x&=& 5 &\mid\; :2,5 \\[5pt]
x&=& 2
\end{array}\)](https://mathjax.schullv.de/144a1ba8cf542223c5d7ee2135dce9f6123d636a89e0d02e0ce892078ea97fc1?color=5a5a5a)
Mit dem zweiten Strahlensatz folgt außerdem:
![\(\begin{array}[t]{rlll}
\dfrac{y}{1,2}&=&\dfrac{8,4}{2,4} &\mid\;\cdot 1,2 \\[5pt]
y&=&2,5\cdot 1,2 & \\[5pt]
y&=& 3
\end{array}\)](https://mathjax.schullv.de/69b42befbfdeeaee683f5dd7d6f10e855b98fac3bf4e29ad3f1e0e6be0bb408c?color=5a5a5a)
d)
Mit der Erweiterun des 1. Strahlensatz gilt:
![\(\begin{array}[t]{rlll}
\dfrac{6,9}{4,6}&=& \dfrac{y}{5} &\mid\; \cdot 5 \\[5pt]
1,5 \cdot 5 &=& y & \\[5pt]
7,5&=& y
\end{array}\)](https://mathjax.schullv.de/53153765ad13c22a66d555280693fb6a6a8d9620ded58c2623c517297f38e4c1?color=5a5a5a)
Mit der Erweiterung des 2. Strahlensatz folgt außerdem:
![\(\begin{array}[t]{rlll}
\dfrac{5,1}{x}&=& \dfrac{6,9}{4,6} &\mid\; \cdot x \\[5pt]
5,1&=& 1,5\cdot x &\mid\; :1,5 \\[5pt]
3,4&=& x
\end{array}\)](https://mathjax.schullv.de/45645fd2d0ae85bfece4de367f4712a6e0628f80e32c231c70de97d7b7df4291?color=5a5a5a)
2
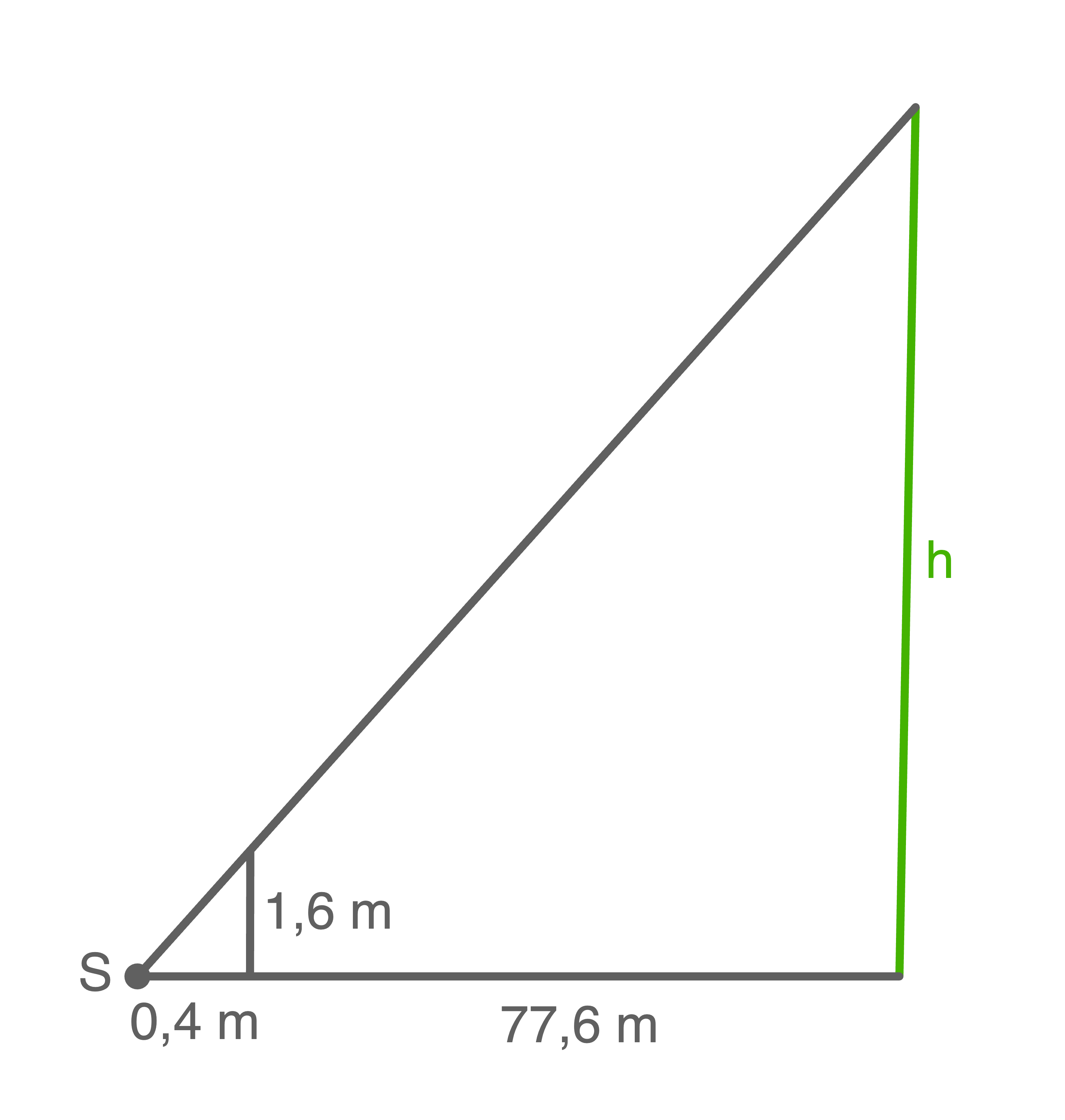
Hilfsskizze