Lineare Gleichungen mit zwei Variablen
Definition
Eine lineare Gleichung mit zwei Variablen ist eine Gleichung der Form- Jede Lösung ist durch ein Zahlenpaar
gegeben
- Jede Gleichung hat unendlich viele verschiedene Lösungen
Grafische Darstellung
Jede Gleichung der Form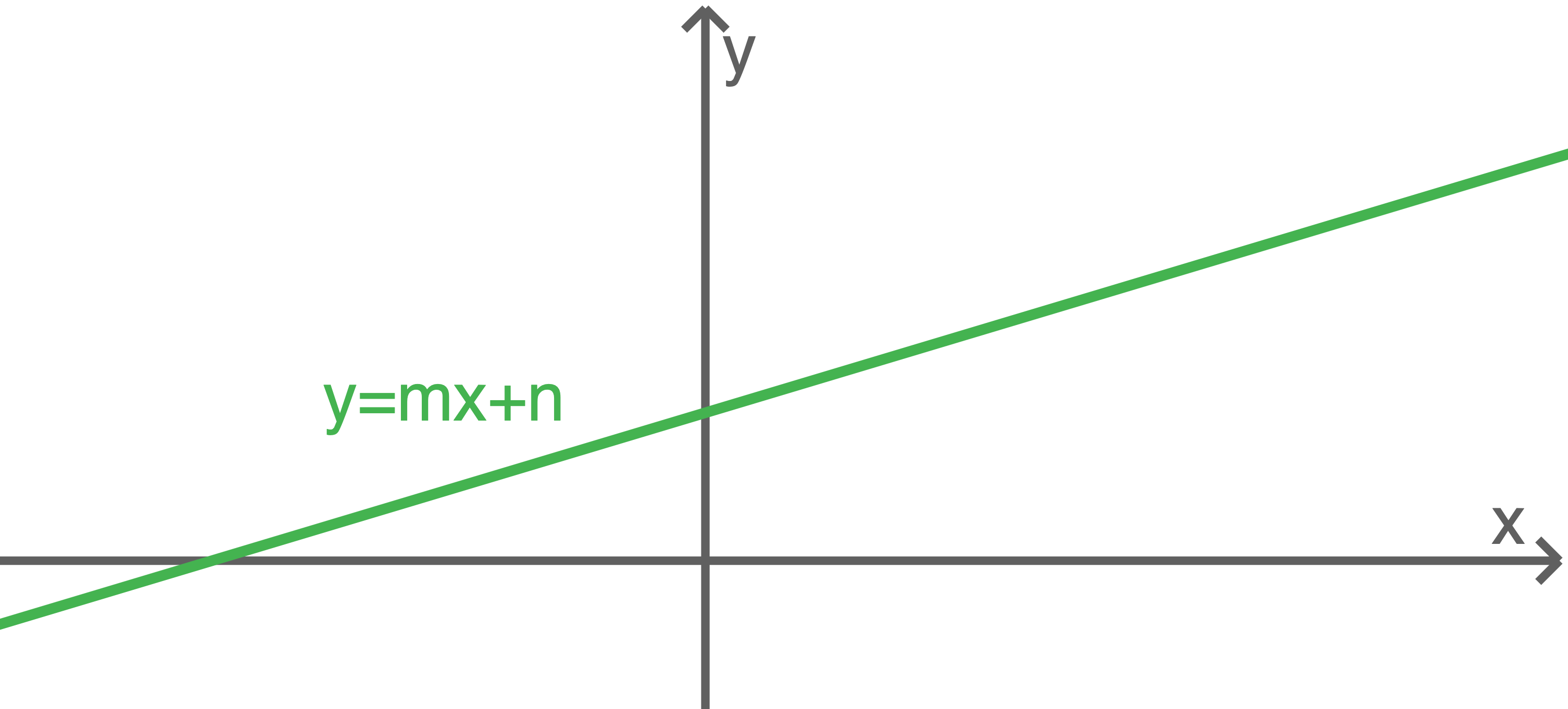
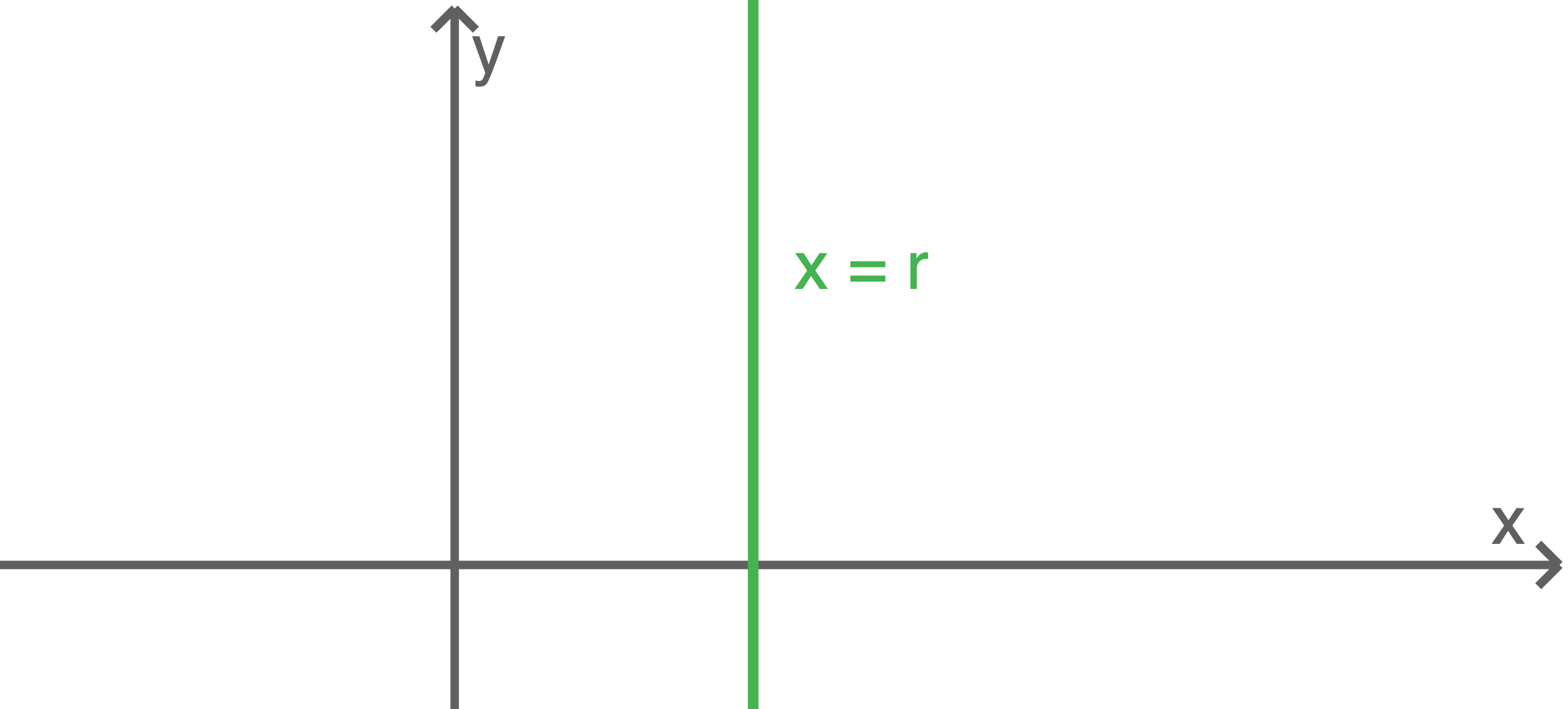
Beispiel:  Es gilt:
Es gilt:
![\(\begin{array}[t]{rlll}
4x+2y&=& 8&\quad \mid\;-4x \\[5pt]
2y&=& 8-4x&\quad \mid\;:2 \\[5pt]
y&=&-2x+4
\end{array}\)](https://www.schullv.de/resources/formulas/1a95be783c000c9003e0996bcb6f85ffbe918756b4f3082f5f76270bca046c4d_light.svg)
Beispiel:  Es gilt:
Es gilt:
![\(\begin{array}[t]{rlll}
2x+0y&=& 6& \\[5pt]
2x&=& 6&\quad \mid\;:2 \\[5pt]
x&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/126c33fea8f49f7b4e66cb7fbea9b3f89c0a0394395925bf911d03a2edb8f7bd_light.svg)
1
Ermittle jeweils zwei Lösungen der linearen Gleichung durch Einsetzen verschiedener  -Werte und zeichne die entsprechende Gerade, welche die lineare Gleichung löst, in ein geeignetes Koordinatensystem ein.
-Werte und zeichne die entsprechende Gerade, welche die lineare Gleichung löst, in ein geeignetes Koordinatensystem ein.




a)
b)
c)
d)
2
Frau Huber ist Sportlehrerin und wird damit beauftragt, neue Fuß- und Basketbälle für die Ausrüstung der Sporthalle zu kaufen. Dafür bekommt sie von der Schule ein Budget von  gestellt.
gestellt.
a)
Stelle eine lineare Gleichung auf, die den Sachzusammenhang beschreibt, wenn ein Fußball jeweils  und ein Basketball jeweils
und ein Basketball jeweils  kostet.
kostet.
b)
Gib drei Lösungen der linearen Gleichung an, die im Sachzusammenhang Sinn ergeben.
c)
Frau Huber handelt mit dem Verkäufer ein Angebot aus, sodass sie für  20 Fußbälle und 10 Basketbälle bekommt.
Welchen Preis kann der Verkäufer für einen Fuß- bzw. Basketball verlangt haben? Gib zwei Möglichkeiten an.
20 Fußbälle und 10 Basketbälle bekommt.
Welchen Preis kann der Verkäufer für einen Fuß- bzw. Basketball verlangt haben? Gib zwei Möglichkeiten an.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Auflösen der Gleichung nach  ergibt:
ergibt:
![\(\begin{array}[t]{rlll}
x-3y&=&9 &\mid\;-x \\[5pt]
-3y&=&9-x &\mid\;:(-3) \\[5pt]
y&=&\dfrac{1}{3}x-3
\end{array}\)](https://www.schullv.de/resources/formulas/4576f3028b44301c794fb93d9f96682750c9600f583a99e7f95a7954543a1ebf_light.svg) Einsetzen von verschiedenen
Einsetzen von verschiedenen  -Werten liefert beispielsweise:
Für
-Werten liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=&\dfrac{1}{3}\cdot0-3 \\[5pt]
&=&-3
\end{array}\)](https://www.schullv.de/resources/formulas/ca86137d2ff5f9d10b02196c27636b2796397ca5a8086f69c7d65cb36dc2f863_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=&\dfrac{1}{3}\cdot3-3 \\[5pt]
&=&-2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ddb226a44f4e7e0a0d3fc459f8bb1f15e6064c13ad5a167f05e445cdaeb09713_light.svg) Durch Einzeichnen und Verbinden der berechneten Punkte
Durch Einzeichnen und Verbinden der berechneten Punkte  und
und  folgt die eindeutig festgelegte Gerade:
folgt die eindeutig festgelegte Gerade:
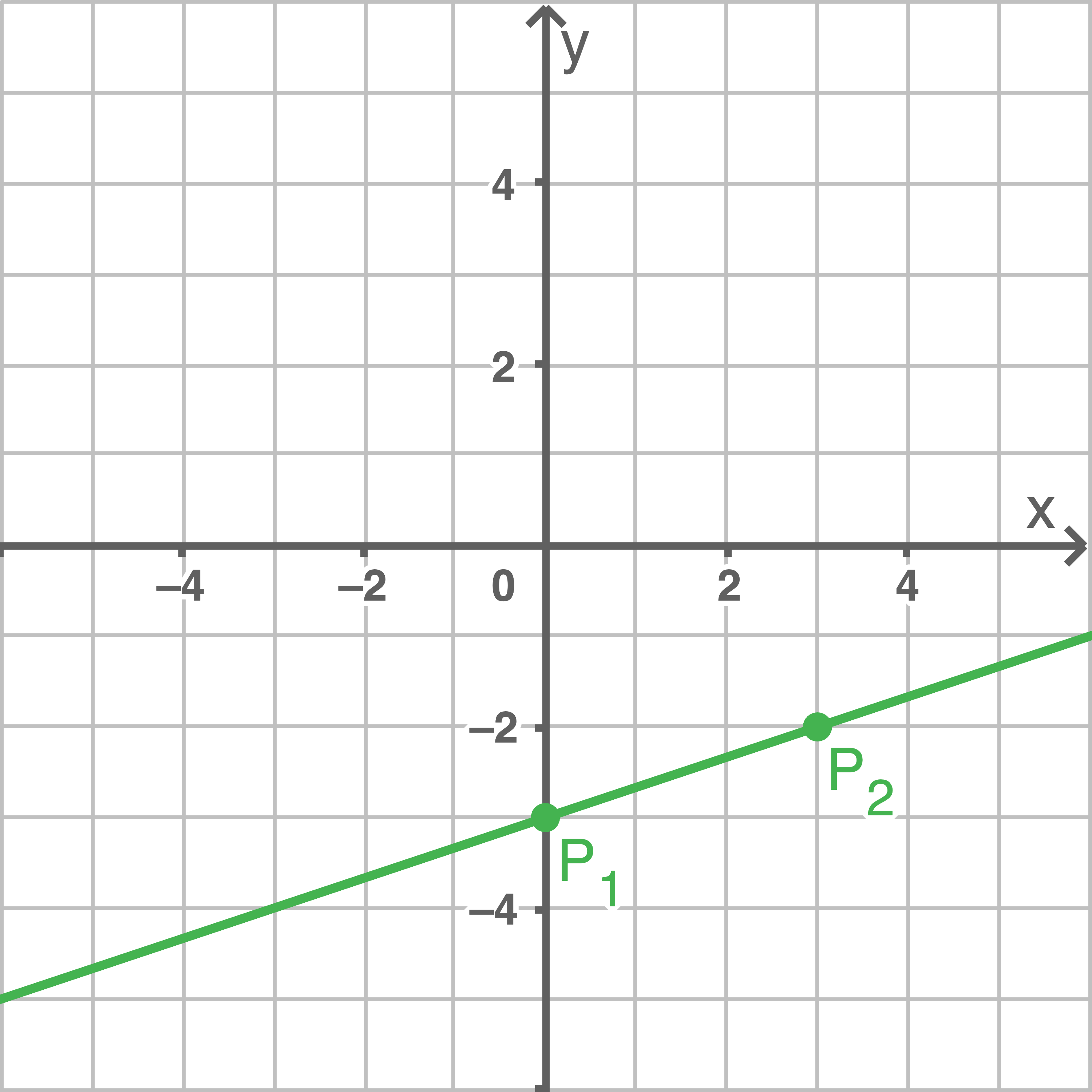

b)
Auflösen der Gleichung nach  ergibt:
ergibt:
![\(\begin{array}[t]{rlll}
5x+2y&=&4 &\mid\;-5x \\[5pt]
2y&=&4-5x &\mid\;:2 \\[5pt]
y&=&-\dfrac{5}{2}x+2
\end{array}\)](https://www.schullv.de/resources/formulas/4c1bbbad623c45fec937bc126db227bbc80ed504abf9515c18dce0de5f28c873_light.svg) Einsetzen von verschiedenen
Einsetzen von verschiedenen  -Werten liefert beispielsweise:
Für
-Werten liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=&-\dfrac{5}{2}\cdot0+2 \\[5pt]
&=&2
\end{array}\)](https://www.schullv.de/resources/formulas/8502900b411af877746fe854ba6ae61cf68e020f6b7dd8a8bc338dc2abc0acbf_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=&-\dfrac{5}{2}\cdot2+2 \\[5pt]
&=&-3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/30e602c6cd21c0e845503ca4d245e015a342c5933035c5a36a7c8aa134c17d8c_light.svg) Durch Einzeichnen und Verbinden der berechneten Punkte
Durch Einzeichnen und Verbinden der berechneten Punkte  und
und  folgt die eindeutig festgelegte Gerade:
folgt die eindeutig festgelegte Gerade:
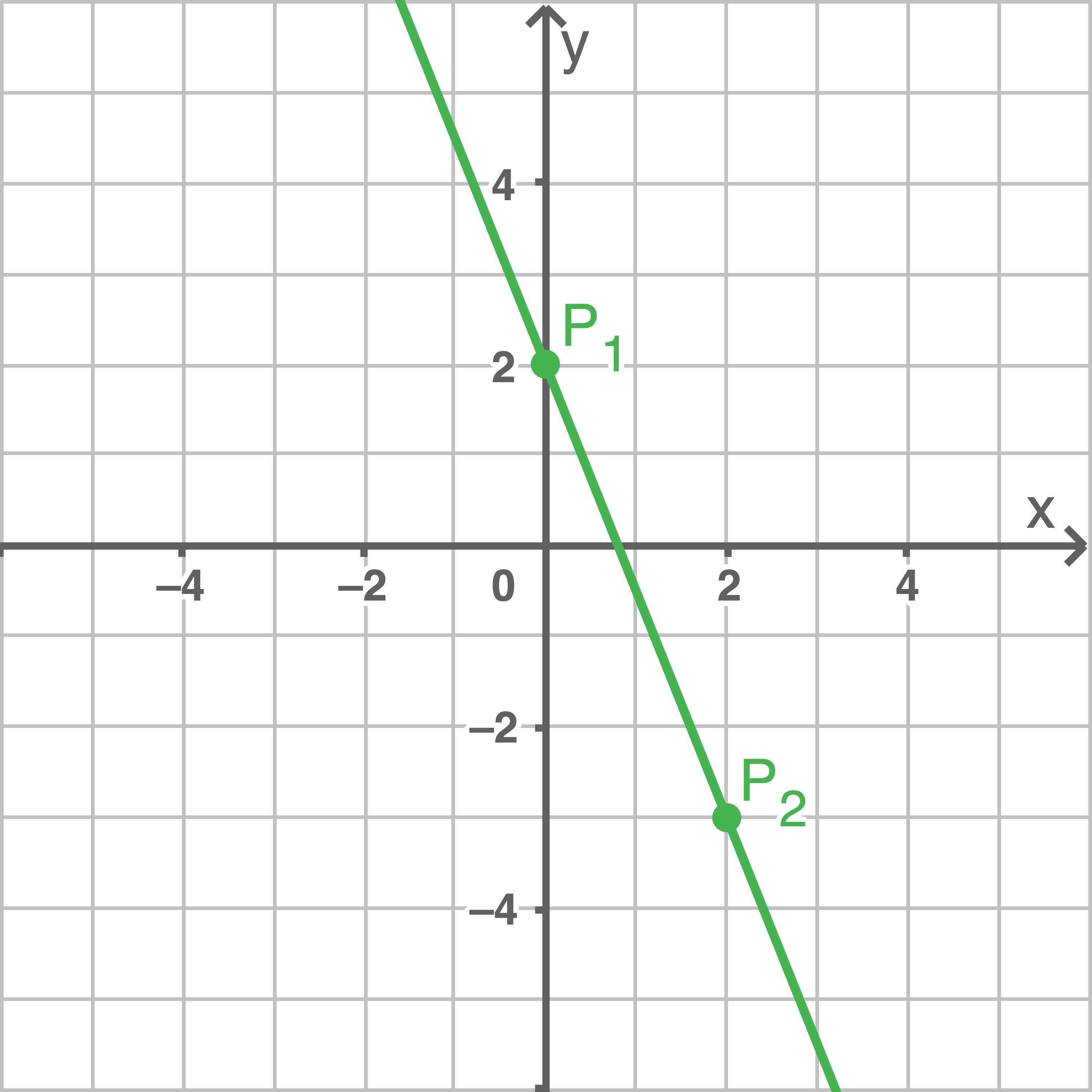

c)
Auflösen der Gleichung nach  ergibt:
ergibt:
![\(\begin{array}[t]{rlll}
-4x-5y&=&0 &\mid\;+4x \\[5pt]
-5y&=&4x &\mid\;:(-5) \\[5pt]
y&=&-\dfrac{4}{5}x
\end{array}\)](https://www.schullv.de/resources/formulas/a9ae6528889d8c9bacfac3851179b496ba7707fb28125b50177f21bb0cc199f5_light.svg) Einsetzen von verschiedenen
Einsetzen von verschiedenen  -Werten liefert beispielsweise:
Für
-Werten liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=&-\dfrac{4}{5}\cdot0 \\[5pt]
&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/23751c7cdd84444f34e52adac3f64e0bbb850fdd66003a99c3b80d9b00e4d9d4_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=&-\dfrac{4}{5}\cdot5 \\[5pt]
&=&-4 \\[5pt]
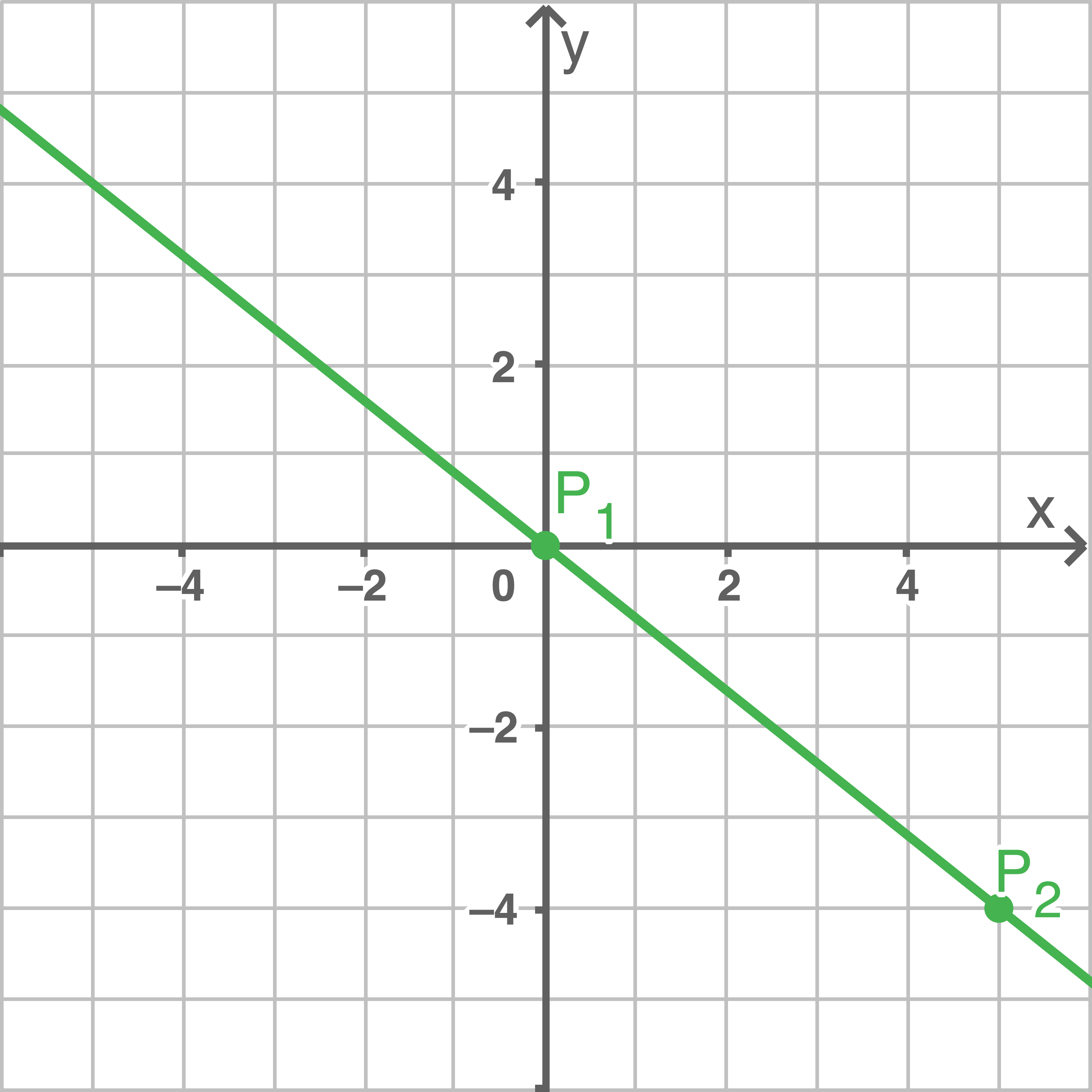
\end{array}\)](https://www.schullv.de/resources/formulas/b11905e44d4bc4daa7fd1844b9e5f86a516d2653d83a32ce108bfc004a65daaa_light.svg) Durch Einzeichnen und Verbinden der berechneten Punkte
Durch Einzeichnen und Verbinden der berechneten Punkte  und
und  folgt die eindeutig festgelegte Gerade:
folgt die eindeutig festgelegte Gerade:

d)
Auflösen der Gleichung nach  ergibt:
ergibt:
![\(\begin{array}[t]{rlll}
2x-6y&=&3 &\mid\;-2x \\[5pt]
-6y&=&3-2x &\mid\;:(-6) \\[5pt]
y&=&\dfrac{1}{3}x-\dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/333bd6e87d5ad01f51f992022d22681c8e3410e27f331d93b9e508906d704860_light.svg) Einsetzen von verschiedenen
Einsetzen von verschiedenen  -Werten liefert beispielsweise:
Für
-Werten liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=&\dfrac{1}{3}\cdot0-\dfrac{1}{2} \\[5pt]
&=&-0,5
\end{array}\)](https://www.schullv.de/resources/formulas/bf1d1f302e00866ef3620779648abe2c16846aae8c37683bd500241da32b971d_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=&\dfrac{1}{3}\cdot3-\dfrac{1}{2} \\[5pt]
&=&0,5 \\[5pt]
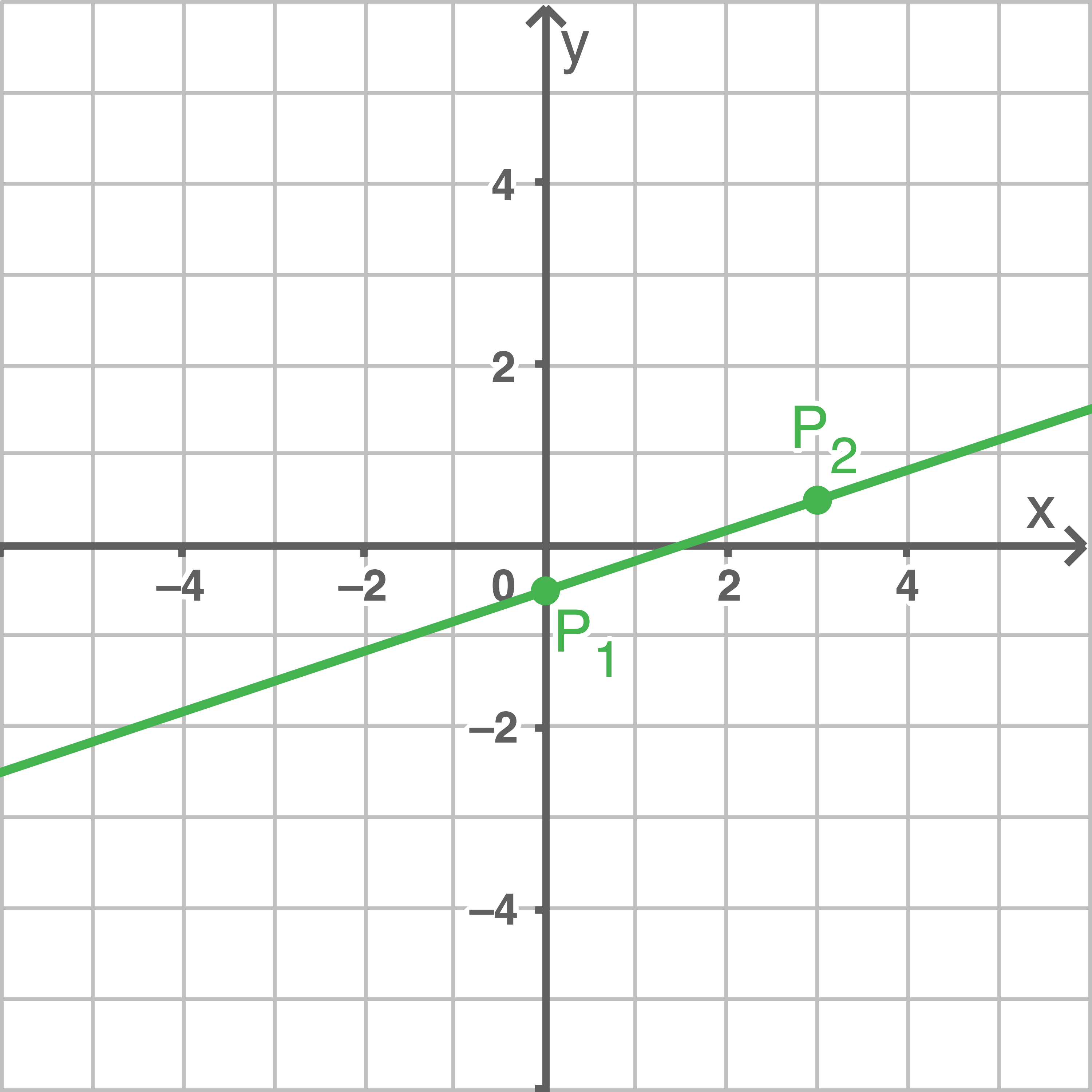
\end{array}\)](https://www.schullv.de/resources/formulas/6715db76b0d0a6f152bf3a94d435713cfff8eee375289bd528c76860425b779e_light.svg) Durch Einzeichnen und Verbinden der berechneten Punkte
Durch Einzeichnen und Verbinden der berechneten Punkte  und
und  folgt die eindeutig festgelegte Gerade:
folgt die eindeutig festgelegte Gerade:

2
a)
Die Variable  beschreibt die Anzahl der gekauften Fußbälle und die Variable
beschreibt die Anzahl der gekauften Fußbälle und die Variable  die Anzahl der gekauften Basketbälle.
Mit den gegebenen Informationen ergibt sich folgende lineare Gleichung:
die Anzahl der gekauften Basketbälle.
Mit den gegebenen Informationen ergibt sich folgende lineare Gleichung:
![\(\begin{array}[t]{rlll}
x\cdot 15+y\cdot 20&=& 350 & \quad \mid\; :5\\[5pt]
3x+4y&=& 70
\end{array}\)](https://www.schullv.de/resources/formulas/470cdeaf1c0cbbaa549e8bdd1193ca393847d1ba006ce7b9139cdef24df350ed_light.svg)
b)
Auflösen der Gleichung nach  ergibt:
ergibt:
![\(\begin{array}[t]{rlll}
3x+4y&=& 70& \quad \mid\; -3x\\[5pt]
4y&=& 70-3x& \quad \mid\; :4\\[5pt]
y&=& 17,5-0,75x
\end{array}\)](https://www.schullv.de/resources/formulas/643a30c34136a23d28038d37dd6b3ed65a6b9cac0141df581b819a2ca3616807_light.svg) Einsetzen von verschiedenen
Einsetzen von verschiedenen  -Werten liefert beispielsweise:
Für
-Werten liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=& 17,5-0,75\cdot 6 \\[5pt]
&=& 13
\end{array}\)](https://www.schullv.de/resources/formulas/dad250dc50613feef0eb15ea80010e8214db1ec28974f8e8c978ecfaab36885f_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=& 17,5-0,75\cdot 10 \\[5pt]
&=& 10
\end{array}\)](https://www.schullv.de/resources/formulas/87cf5a7d6571499ea4136184324a6685a8c1b9fc49c92f8061c5d67992730d4e_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=& 17,5-0,75\cdot 14 \\[5pt]
&=& 7
\end{array}\)](https://www.schullv.de/resources/formulas/1b896ded5d06288bac27b51c81be068aa836bd97d10abcc350e436ff2dfd1892_light.svg) Mögliche Lösungen sind somit
Mögliche Lösungen sind somit 
 und
und 
c)
Durch das Angebot wird die Anzahl der Bälle eindeutig festgelegt, während die neuen Sonderpreise unbekannt sind. Definiere also:
 Sonderpreis für einen Fußball in
Sonderpreis für einen Fußball in 
 Sonderpreis für einen Basketball in
Sonderpreis für einen Basketball in  Es ergibt sich folgende lineare Gleichung:
Es ergibt sich folgende lineare Gleichung:
![\(\begin{array}[t]{rlll}
20\cdot x+ 10\cdot y&=& 350 &\quad \mid\; :10\\[5pt]
2x+ y&=& 35 &\quad \mid\; -2x\\[5pt]
y&=& 35-2x
\end{array}\)](https://www.schullv.de/resources/formulas/1e6bcab24e430ae0f52703defe3437a56d9d1d179525ab47369b5353ea48fd30_light.svg) Einsetzen verschiedener
Einsetzen verschiedener  -Werte liefert beispielsweise:
Für
-Werte liefert beispielsweise:
Für 
![\(\begin{array}[t]{rlll}
y&=& 35-2\cdot 10 \\[5pt]
&=& 15
\end{array}\)](https://www.schullv.de/resources/formulas/ec63b5fb02c3a5c53ad67a6497f8ea58affbec7d6d415123e5999d0aad3ed3da_light.svg) Für
Für 
![\(\begin{array}[t]{rlll}
y&=& 35-2\cdot 11 \\[5pt]
&=& 13
\end{array}\)](https://www.schullv.de/resources/formulas/b23ac23c21e82194a1242ad83716655bede10c08b721498e19129dd158785287_light.svg) Der Händler kann bei dem Angebot beispielsweise
Der Händler kann bei dem Angebot beispielsweise  für einen Fußball und
für einen Fußball und  für einen Basketball oder
für einen Basketball oder  für einen Fußball und
für einen Fußball und  für einen Basketball verlangt haben.
für einen Basketball verlangt haben.