Quadratische Funktionen anwenden
Im Alltag ist es oft wichtig zu wissen, wann eine Größe, wie beispielsweise der Gewinn, die Höhe eines Flugs oder ein Flächeninhalt, ihren größten oder kleinsten Wert erreicht. Solche Fragestellungen lassen sich häufig mit quadratischen Funktionen beschreiben und werden als Optimierungsprobleme bezeichnet.
Der Scheitelpunkt der zugehörigen Parabel liefert dabei den maximalen oder minimalen Wert der Funktion.
 und
und  zu wählen, damit der Inhalt des Rechtecks maximal wird?
1. Schritt: Variable einführen
zu wählen, damit der Inhalt des Rechtecks maximal wird?
1. Schritt: Variable einführen
 Länge der Querseiten
Länge der Querseiten  und
und  in Metern
2. Schritt: Quadratische Gleichung aufstellen
Da die Gesamtlänge des Seils
in Metern
2. Schritt: Quadratische Gleichung aufstellen
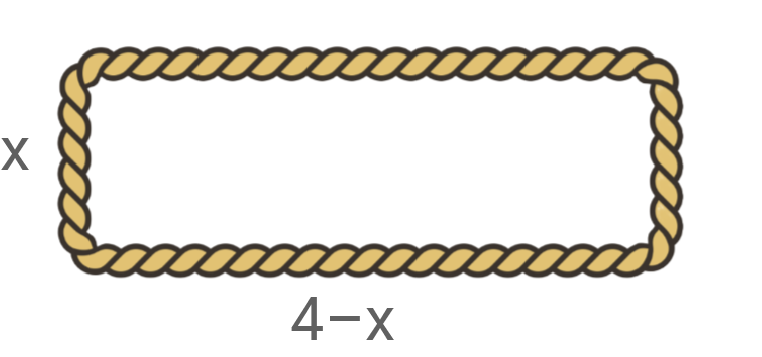
Da die Gesamtlänge des Seils  Meter beträgt und die beiden Querseiten jeweils eine Länge von
Meter beträgt und die beiden Querseiten jeweils eine Länge von  Metern haben, bleiben für die beiden Längsseiten
Metern haben, bleiben für die beiden Längsseiten  Meter übrig.
Meter übrig.
 3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
![\(\begin{array}[t]{rlll}
A&=& x\cdot (4-x) & \\[5pt]
&=& -x^2+4x
\end{array}\)](https://www.schullv.de/resources/formulas/28b7f2441a6b247f582ed276c0d23890429195d12bd24f18d3dfd125f7f449a3_light.svg) Mit quadratischer Ergänzung ergibt sich:
Mit quadratischer Ergänzung ergibt sich:
![\(\begin{array}[t]{rlll}
A&=& -(x^2-4x) & \\[5pt]
&=& -\left(x^2-4x+\left(\dfrac{4}{2}\right)^2 -\left(\dfrac{4}{2}\right)^2\right) & \\[5pt]
&=& -\left(\left(x-2\right)^2-4\right) & \\[5pt]
&=&-\left(x-2\right)^2+4
\end{array}\)](https://www.schullv.de/resources/formulas/858028d728643745a3afb3cd1d47a6a4c77afc5af36428b9b9535d158aa7aba7_light.svg) Aus der Scheitelform kann der Scheitelpunkt
Aus der Scheitelform kann der Scheitelpunkt  direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die
direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die  -Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle
-Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle  um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt.
Für die Längseite des Rechtecks gilt für
um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt.
Für die Längseite des Rechtecks gilt für 
 5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Querseite von
5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Querseite von  und einer Länge der Längsseite von
und einer Länge der Längsseite von  ist der Flächeninhalt des Rechtecks somit maximal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
ist der Flächeninhalt des Rechtecks somit maximal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
Vorgehen
- Variable einführen
- Quadratische Gleichung aufstellen
- Scheitelpunkt bestimmen
- Ergebnis angeben
- Lösung im Sachzusammenhang prüfen
Beispiel
Ein Seil mit acht Metern Länge soll zu einem Rechteck gelegt werden. Wie sind
Die Länge einer Längsseite ergibt sich also zu:
![\(\dfrac{8-2x}{2}= 4-x \; [\text{m}]\)](https://www.schullv.de/resources/formulas/9ad07178c22fe0c7db42d564a245ea5e2fa7a1c3efb9648cecbfd5fea953f890_light.svg) Für den Flächeninhalt des Rechtecks gilt also:
Für den Flächeninhalt des Rechtecks gilt also:


1
Lena hat sich einen 12 Meter langen Maschendraht gekauft, um einen rechteckigen Platz im Garten für ihre Kaninchen einzuzäunen. Sie benutzt dafür die Wände von ihrem Haus und der Garage.
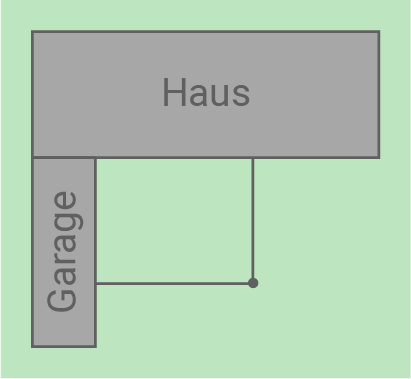
a)
Gib fünf mögliche Zahlenpaare für die Seitenlängen  und
und  des Rechtecks an sowie den jeweils zugehörigen Flächeninhalt
des Rechtecks an sowie den jeweils zugehörigen Flächeninhalt 
b)
Für welche Maße wird der Platz am größten?
c)
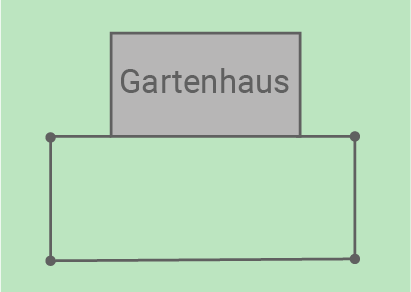
Wie müsste Lena die Maße wählen, wenn sie nur die 4 Meter lange Wand des Gartenhauses zur Abgrenzung verwenden dürfte?
2
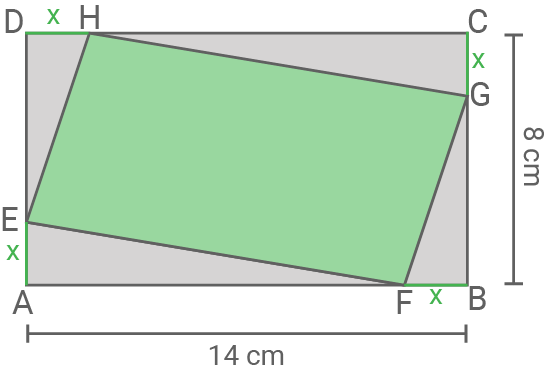
Auf den Seiten des Rechtecks  wird wie in der nebenstehenden Abbildung auf jeder Seite die Länge
wird wie in der nebenstehenden Abbildung auf jeder Seite die Länge  abgetragen, sodass ein Viereck
abgetragen, sodass ein Viereck  entsteht.
entsteht.
a)
Welche besondere Form hat das Viereck 
b)
Für welche Länge  ist der Flächeninhalt des Vierecks am kleinsten?
Hinweis: Welche Flächen müssen von der Fläche des Rechtecks abgezogen werden, sodass man das Viereck
ist der Flächeninhalt des Vierecks am kleinsten?
Hinweis: Welche Flächen müssen von der Fläche des Rechtecks abgezogen werden, sodass man das Viereck  erhält?
erhält?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Mögliche Zahlenpaare sind:
b)
1. Schritt: Variable einführen
 Länge der der Seite
Länge der der Seite  in Metern
2. Schritt: Quadratische Gleichung aufstellen
Da die Gesamtlänge des Zauns
in Metern
2. Schritt: Quadratische Gleichung aufstellen
Da die Gesamtlänge des Zauns  Meter beträgt und die Seite
Meter beträgt und die Seite  eine Länge von
eine Länge von  Metern hat, bleiben für die Sseite
Metern hat, bleiben für die Sseite  noch
noch  Meter übrig.
Für den Flächeninhalt des Rechtecks gilt also:
Meter übrig.
Für den Flächeninhalt des Rechtecks gilt also:
 3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
![\(\begin{array}[t]{rlll}
A&=& x\cdot (12-x) & \\[5pt]
&=& -x^2+12x
\end{array}\)](https://www.schullv.de/resources/formulas/799671119aab3257cb9b4e107c02a8028e904672a08f666e8b3d8999b3149608_light.svg) Mit quadratischer Ergänzung ergibt sich:
Mit quadratischer Ergänzung ergibt sich:
![\(\begin{array}[t]{rlll}
A&=& -(x^2+12x) & \\[5pt]
&=& -\left(x^2+12x+\left(\dfrac{12}{2}\right)^2 -\left(\dfrac{12}{2}\right)^2\right) & \\[5pt]
&=& -\left(\left(x-6\right)^2-36\right) & \\[5pt]
&=&-\left(x-6\right)^2+36
\end{array}\)](https://www.schullv.de/resources/formulas/5506c9b5b0067faab49f938a4baf47f2f6916dfa1fbdc2c33313419db84bc71f_light.svg) Aus der Scheitelform kann der Scheitelpunkt
Aus der Scheitelform kann der Scheitelpunkt  direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die
direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die  -Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle
-Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle  um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt
um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt  Für die Seite
Für die Seite  des Rechtecks gilt für
des Rechtecks gilt für 
![\(12-6=6 \, [\text{m}]\)](https://www.schullv.de/resources/formulas/f4f7becce1aceb19cc133cc165db6ec57dfe2d96eb6ada8352cc960c1e0197c7_light.svg) 5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Seite
5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Seite  von
von  und einer Länge der Seite
und einer Länge der Seite  von
von  ist der Flächeninhalt des Rechtecks somit maximal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
ist der Flächeninhalt des Rechtecks somit maximal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
c)
1. Schritt: Variable einführen
 Länge der Seiten
Länge der Seiten  welche nicht an der Mauer liegen, in Metern
2. Schritt: Quadratische Gleichung aufstellen
Da die Gesamtlänge des Zauns
welche nicht an der Mauer liegen, in Metern
2. Schritt: Quadratische Gleichung aufstellen
Da die Gesamtlänge des Zauns  Meter beträgt und die beiden Seiten
Meter beträgt und die beiden Seiten  jeweils eine Länge von
jeweils eine Länge von  Metern haben,bleiben für die beiden Längsseiten
Metern haben,bleiben für die beiden Längsseiten  Meter übrig. Da das Gartenhaus zusätzlich eine Länge von
Meter übrig. Da das Gartenhaus zusätzlich eine Länge von  Metern zur Abrenzung bietet, ergibt sich die Länge einer Längsseite also zu:
Metern zur Abrenzung bietet, ergibt sich die Länge einer Längsseite also zu:
![\(\dfrac{12-2x+4}{2}= 8-x \; [\text{m}]\)](https://www.schullv.de/resources/formulas/1336ab8fa2dd85eae113fb132f7cf46d4730893385cd5e26534e7a96e262ed60_light.svg) Für den Flächeninhalt des Rechtecks gilt also:
Für den Flächeninhalt des Rechtecks gilt also:
 3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
3. Schritt: Scheitelpunkt bestimmen
Ausmultiplizieren der Funktion für den Flächeninhalt liefert die folgende allgemeine quadratische Funktion:
![\(\begin{array}[t]{rlll}
A&=& x\cdot (8-x) & \\[5pt]
&=& -x^2+8x
\end{array}\)](https://www.schullv.de/resources/formulas/0e6a6de0f5518bc28828cb9213c8f3902aeb88bde9ec9ee6c4c18ed8372aeec6_light.svg) Mit quadratischer Ergänzung ergibt sich:
Mit quadratischer Ergänzung ergibt sich:
![\(\begin{array}[t]{rlll}
A&=& -(x^2-8x) & \\[5pt]
&=& -\left(x^2-8x+\left(\dfrac{8}{2}\right)^2 -\left(\dfrac{8}{2}\right)^2\right) & \\[5pt]
&=& -\left(\left(x-4\right)^2-16\right) & \\[5pt]
&=&-\left(x-4\right)^2+16
\end{array}\)](https://www.schullv.de/resources/formulas/3f7bc33bdca97f4193fb4ce588ed42c4930499779b953195d9a66d48558e2044_light.svg) Aus der Scheitelform kann der Scheitelpunkt
Aus der Scheitelform kann der Scheitelpunkt  direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die
direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die  -Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle
-Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle  um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt.
Für die Längseiten
um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt.
Für die Längseiten  des Rechtecks gilt für
des Rechtecks gilt für 
 5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Seiten
5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Seiten  von jeweils
von jeweils  und einer Länge der Seiten
und einer Länge der Seiten  von
von  ist der Flächeninhalt des Rechtecks somit maximal.
Eine Seite
ist der Flächeninhalt des Rechtecks somit maximal.
Eine Seite  entspricht somit genau der Wand des Gartenhauses.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
entspricht somit genau der Wand des Gartenhauses.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
2
a)
Bei dem inneren Viereck handelt es sich um ein Parallelogramm.
b)
1. Schritt: Variable einführen
 abgetragene Strecke an den Seiten des Rechtecks
abgetragene Strecke an den Seiten des Rechtecks  2. Schritt: Quadratische Gleichung aufstellen
Der Flächeninhalt des Vierecks
2. Schritt: Quadratische Gleichung aufstellen
Der Flächeninhalt des Vierecks  ist genau dann am kleinsten, wenn die gesamte Fläche der Dreiecke, die zwischen
ist genau dann am kleinsten, wenn die gesamte Fläche der Dreiecke, die zwischen  und
und  liegen, maximal ist.
Für den Flächeninhalt der abgetragenen Dreiecke mit der Grundseite von
liegen, maximal ist.
Für den Flächeninhalt der abgetragenen Dreiecke mit der Grundseite von  bzw
bzw  gilt:
gilt:
![\(\begin{array}[t]{rlll}
A_{\text {Dreiecke }}&=& 2 \cdot \left(\frac{1}{2} \cdot x \cdot (8-x)\right)+2 \cdot \left(\frac{1}{2} \cdot x \cdot (14-x)\right)& \\[5pt]
&=& x \cdot (8-x)+ x \cdot (14-x)& \\[5pt]
&=& 8 x-x^2+14 x -x^2& \\[5pt]
&=& -2x^2 +22x & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bb102d41c36593f9883e29c0bc96adc2710121546a1fa3314a1563a2497ba053_light.svg) 3. Schritt: Scheitelpunkt bestimmen
Mit quadratischer Ergänzung ergibt sich:
3. Schritt: Scheitelpunkt bestimmen
Mit quadratischer Ergänzung ergibt sich:
![\(\begin{array}[t]{rlll}
A(x) &=& -2\cdot (x^2 - 11x) & \\[5pt]
&=& -2\cdot \left(x^2-11x+\left(\dfrac{11}{2}\right)^2 -\left(\dfrac{11}{2}\right)^2\right) & \\[5pt]
&=& -2\cdot \left((x - 5,5)^2 - 30,25\right) & \\[5pt]
&=& -2\cdot (x - 5,5)^2 + 60,5 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5670e44e4bef404a316903b3d1ef73e5e5c474078a2957dbe3b26e4062ddd7f7_light.svg) Aus der Scheitelform kann der Scheitelpunkt
Aus der Scheitelform kann der Scheitelpunkt  direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die
direkt abgelesen werden.
Alternativ kann der Scheitelpunkt auch mit dem CAS bestimmt werden.
4. Schritt: Ergebnis angeben
Die  -Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle
-Koordinate des Scheitelpunkts ist der kleinste bzw. größte Funktionswert des Rechtecks. Da die Parabel nach unten geöffnet ist, handelt es sich an der Stelle  um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt der Dreiecke.
5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Strecke
um den Hochpunkt der Parabel und somit um den maximalen Flächeninhalt der Dreiecke.
5. Schritt: Lösung im Sachzusammenhang prüfen
Für eine Länge der Strecke  von
von  ist der Flächeninhalt des Vierecks
ist der Flächeninhalt des Vierecks  somit minimal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.
somit minimal.
Da dies positive, realistische Längen sind, ist die Lösung sinnvoll.