Grafisches Lösungsverfahren

Für alle quadratischen Gleichungen, die in der Normalform $x^2+p x+q=0$ gegeben sind oder in diese umgeschrieben werden können, gibt es zwei annähernde, grafische Lösungsverfahren.

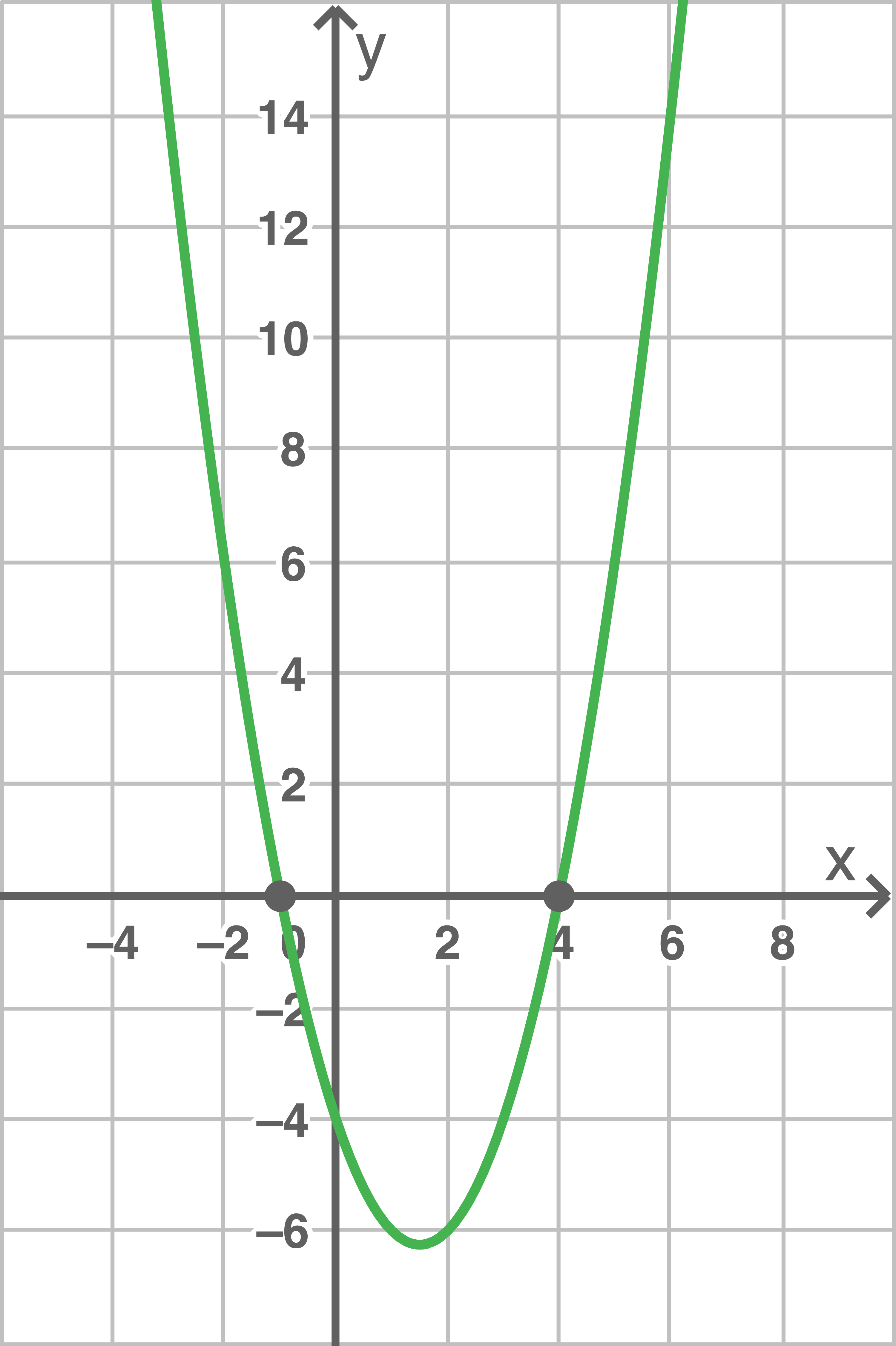
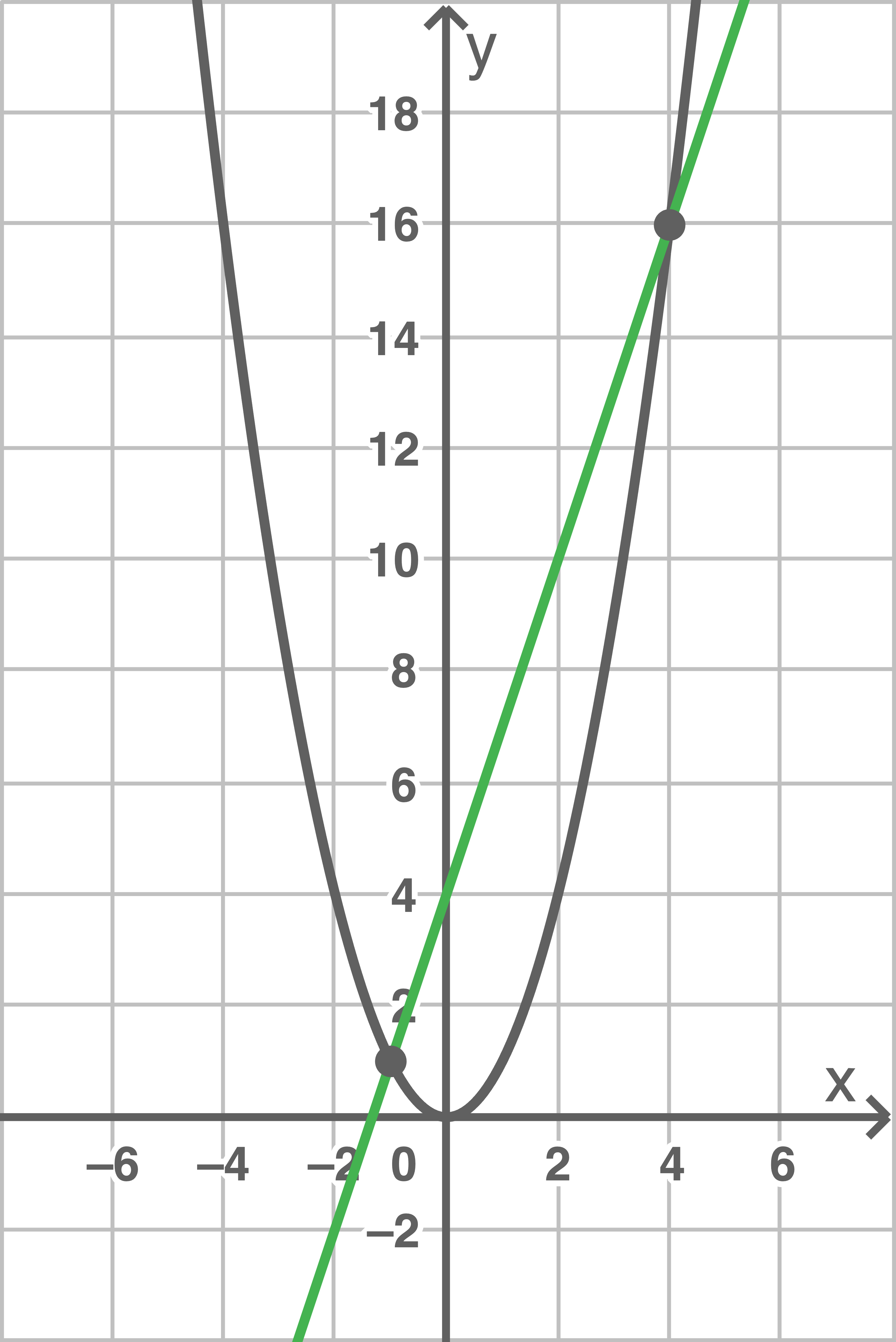
Näherungsverfahren mit CAS

Die Lösungen der Gleichung $x^2+p x+q=0$ entsprechen den Nullstellen der quadratischen Funktion $y=x^2+p x+q.$

Mit dem CAS kann der Graph der Funktion dargestellt und die Nullstellen abgelesen werden.

Beispiel:

$\begin{array}[t]{rlll} x^2-3x-4 &=& 0 &\mid\; CAS \\[5pt] x_1 &=& -1 & \\[5pt] x_2 &=& 4 \end{array}$

Graf einer Parabel mit Koordinatensystem, zeigt positive und negative y-Werte.

Zeichnerisches Näherungsverfahren ohne CAS

Umformen der quadratischen Gleichung liefert folgende Form:

$\begin{array}[t]{rlll} x^2+p x+q &=& 0 &\mid\; -px \mid\; -q \\[5pt] x^2&=& -px-q \end{array}$

Die linke Seite der Gleichung entspricht einer Geraden mit der Steigung $-p$ und dem $y$ -Achsenabschnitt $-q.$ Die rechte Seite der Gleichung beschreibt eine Normalparabel.

Durch das Einzeichnen der Gerade und der Normalparabel in ein gemeinsames Koordinatensystem können die Schnittpunkte näherungsweise abgelesen werden. Die $x$ -Koordinaten der Schnittpunkte entsprechen den Lösungen der quadratischen Gleichung.

Beispiel:

$\begin{array}[t]{rlll} x^2-3x-4 &=& 0 &\mid\; +3x \mid\; +4 \\[5pt] x^2 &=& 3x+4 & \\[5pt] x_1 &=& -1 & \\[5pt] x_2 &=& 4 \end{array}$

Graph einer Parabel mit einer grünen Geraden, die die Parabel schneidet. Achsen sind beschriftet.

Löse die quadratische Gleichung grafisch mit dem CAS.

Für die Funktion $y=x^2-7 x+12$ liefert der CAS folgende grafische Darstellung:

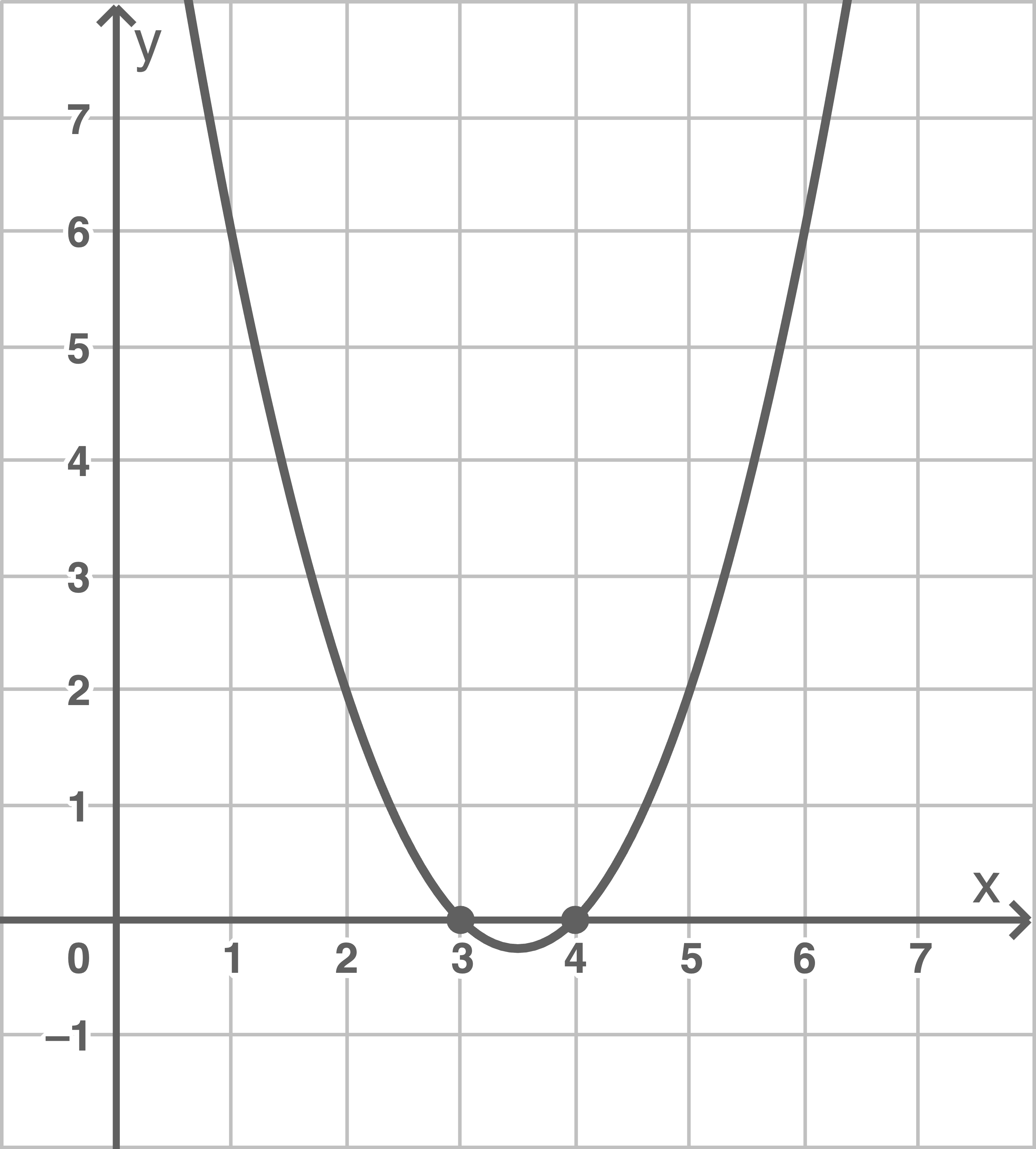Graf einer Parabel im Koordinatensystem mit Achsenbeschriftung.

Die Nullstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=3$ und $x_2=4.$

Für die Funktion $y=x^2+5 x+6$ liefert der CAS folgende grafische Darstellung:

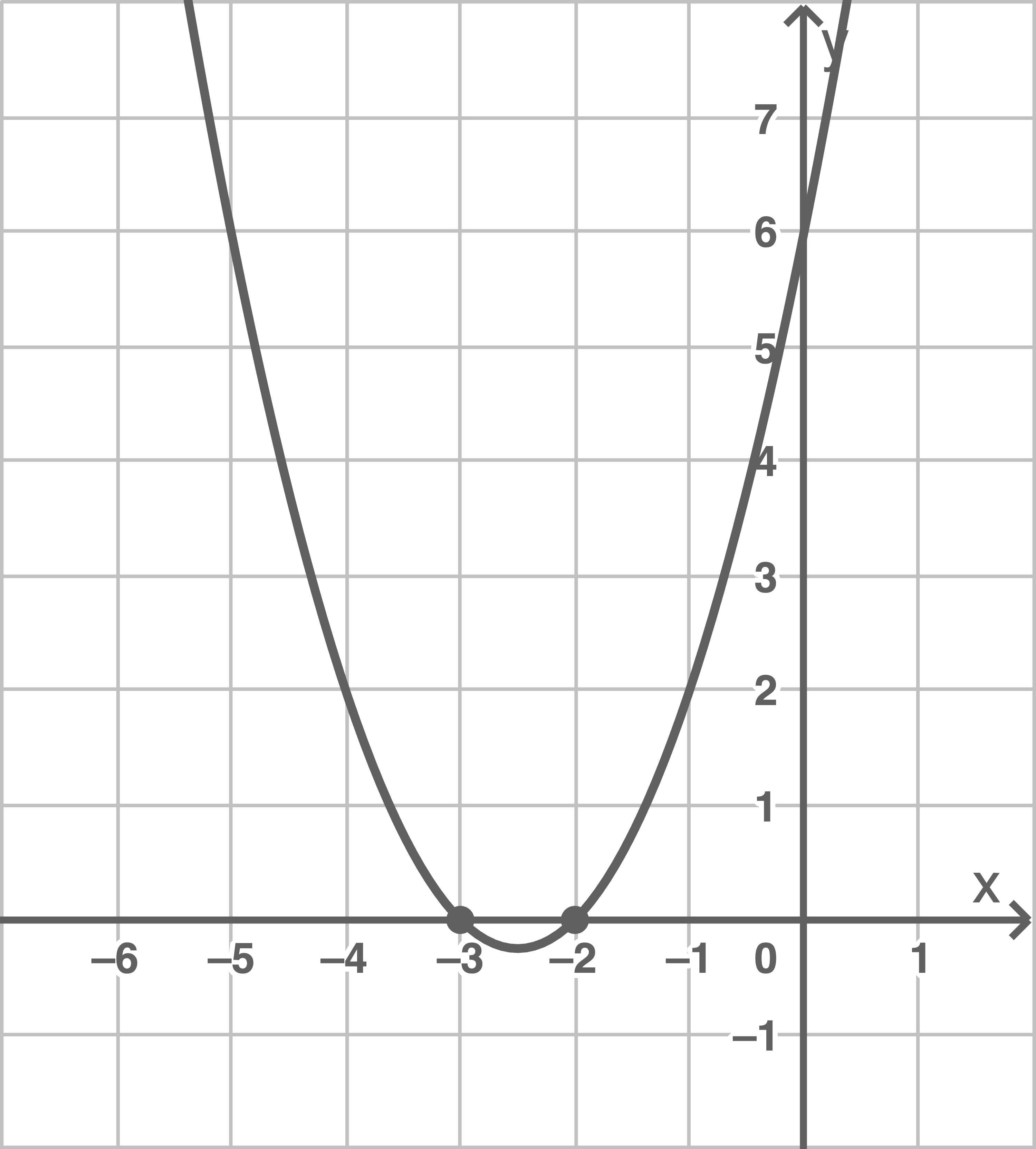Graph einer Parabel im Koordinatensystem mit Achsen und Gitterlinien.

Die Nullstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=-2$ und $x_2=-3.$

Es gilt:

$\begin{array}[t]{rlll} -x^2+6 x&=& 8 &\mid\; -8 \\[5pt] -x^2+6x-8&=& 0 \end{array}$

Für die Funktion $y=-x^2+6x-8$ liefert der CAS folgende grafische Darstellung:

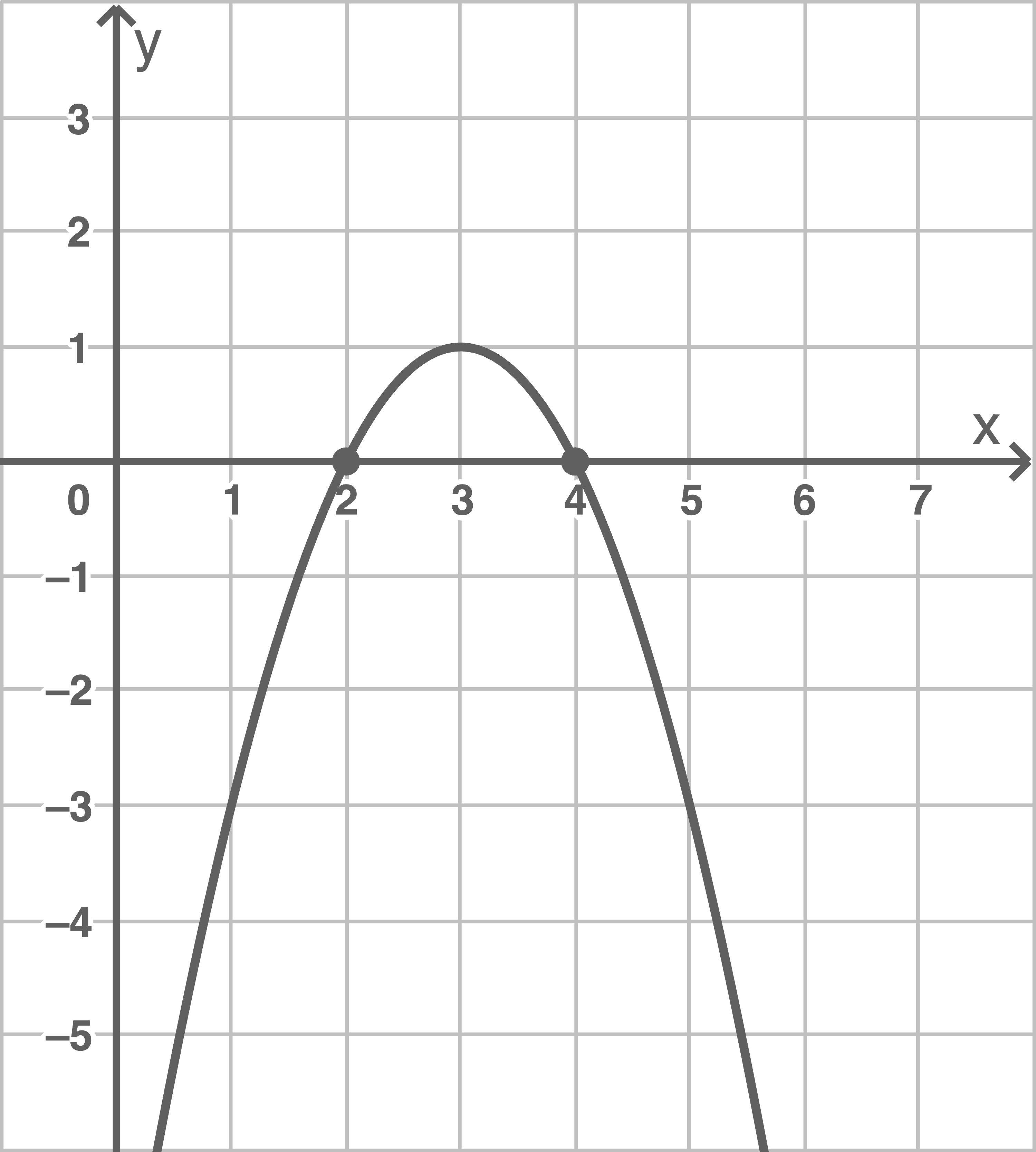Graph einer Parabel im Koordinatensystem mit x- und y-Achse.

Die Nullstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=2$ und $x_2=4.$

Es gilt:

$\begin{array}[t]{rlll} 2 x^2-4 x+4&=& 4x-2 &\mid\; -4x\mid\; +2 \\[5pt] 2x^2-8x+2 &=& 0 \end{array}$

Für die Funktion $y=2x^2-8x+2$ liefert der CAS folgende grafische Darstellung:

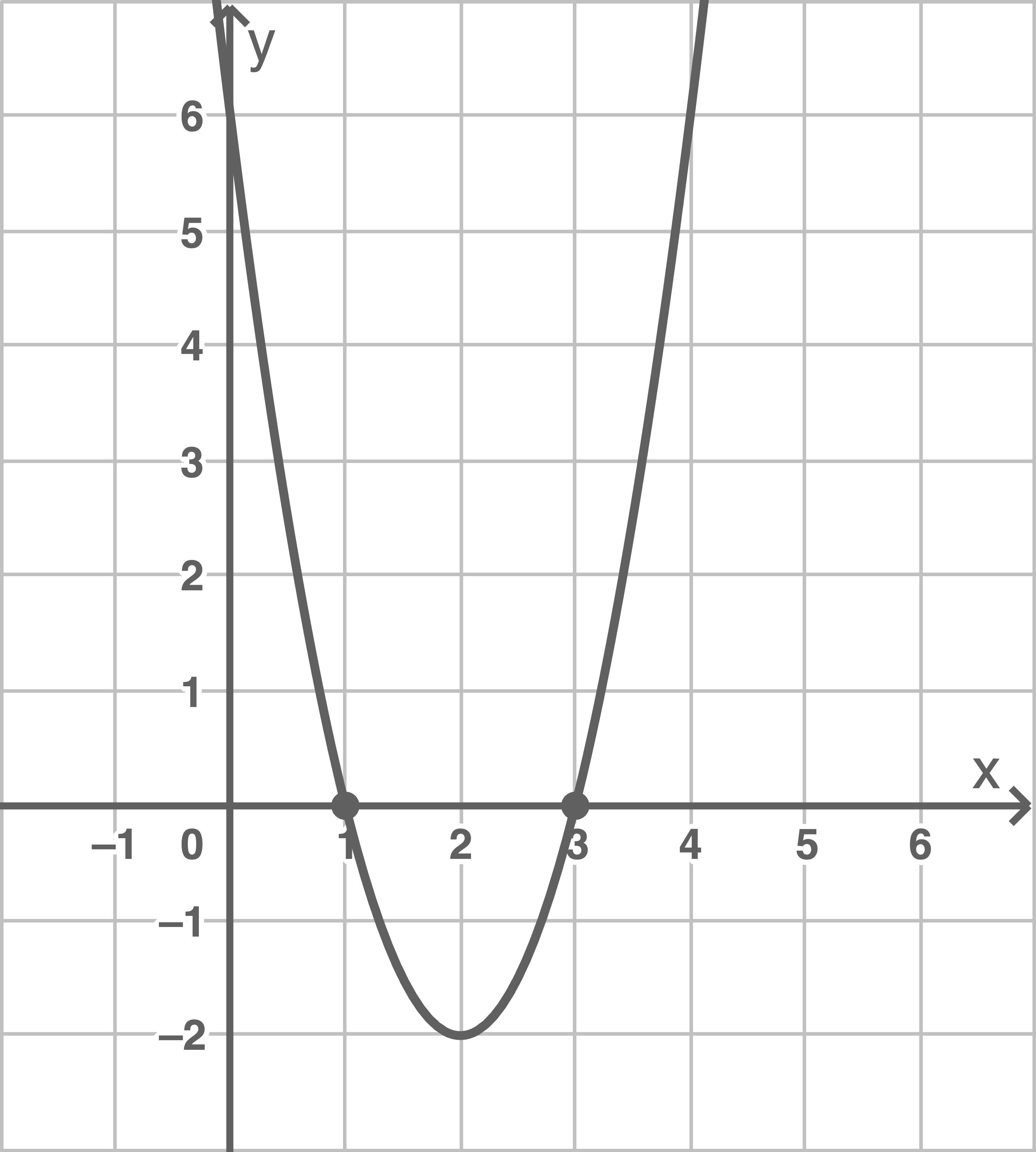Parabelgraf auf einem Koordinatensystem mit Achsenbeschriftungen.

Die Nullstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=1$ und $x_2=3.$

Umformen der Gleichung ergibt:

$\begin{array}[t]{rlll} x^2-x-6&=& 0 &\mid\; +x \mid\; +6\\[5pt] x^2 &=& x+6 \end{array}$

Einzeichnen der Normalparabel $x^2$ und der Geraden mit der Gleichung $y=x+6$ in ein gemeinsames Koordinatensystem liefert:

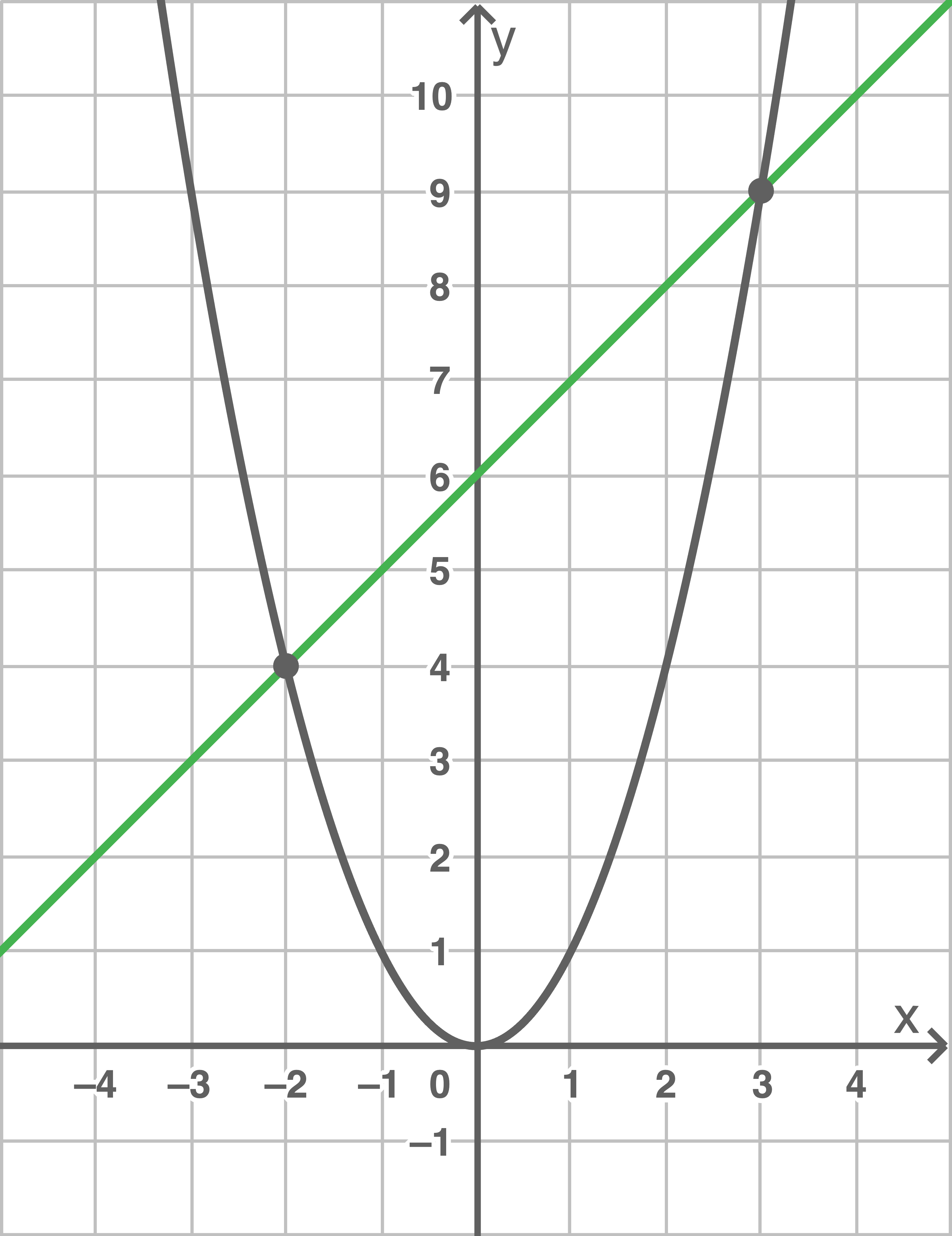Grafische Darstellung einer Parabel und einer Geraden im Koordinatensystem.

Die Schnittstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=-2$ und $x_2=3.$

Umformen der Gleichung ergibt:

$\begin{array}[t]{rlll} 3x^2-12x+9&=& 0 &\mid\; +12x \mid\; -9\\[5pt] 3x^2&=& 12x-9 &\mid\; :3 \\[5pt] x^2&=& 4x-3 \end{array}$

Einzeichnen der Normalparabel $x^2$ und der Geraden mit der Gleichung $y=4x-3$ in ein gemeinsames Koordinatensystem liefert:

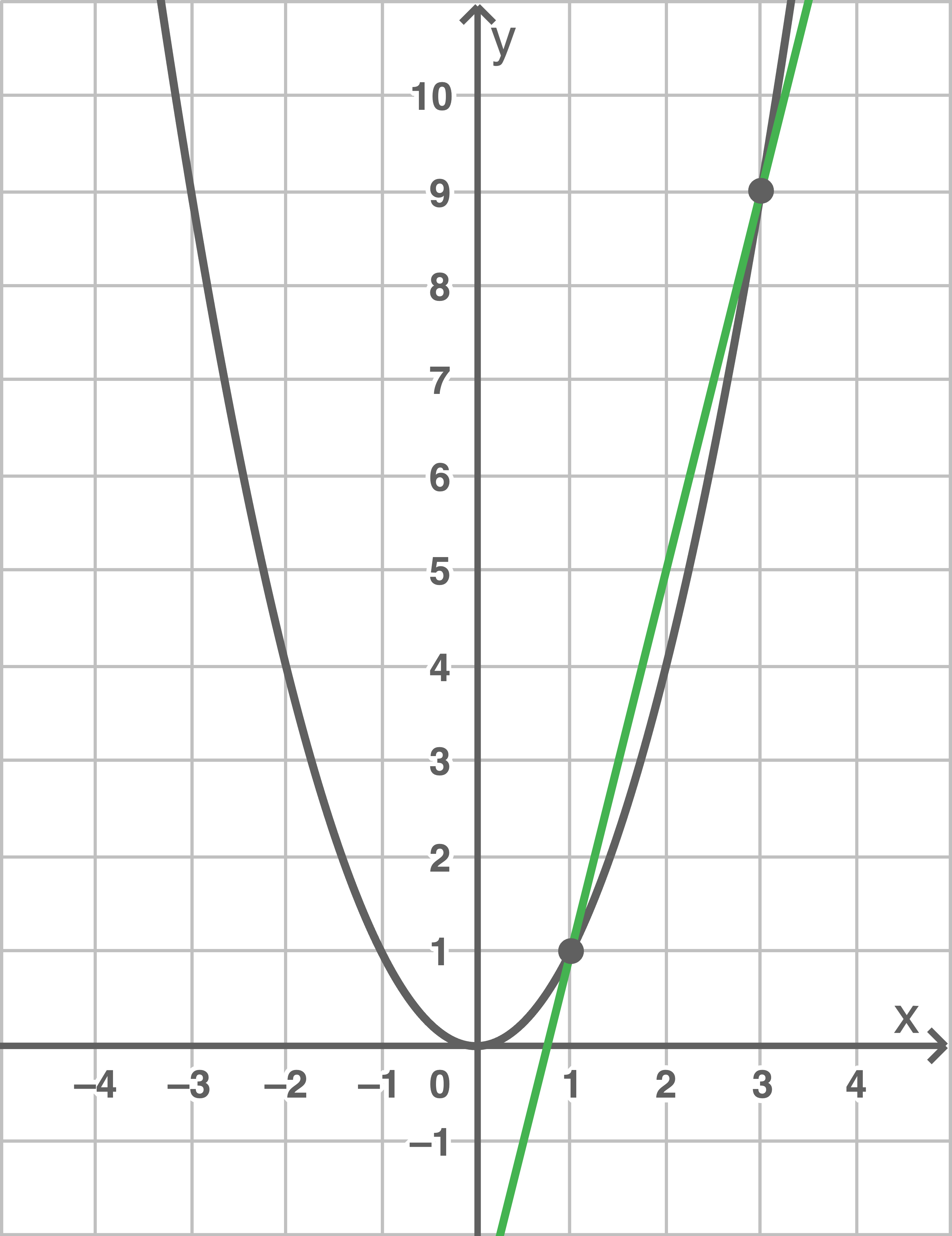Graph einer Parabel und einer Geraden im Koordinatensystem.

Die Schnittstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=1$ und $x_2=3.$

Umformen der Gleichung ergibt:

$\begin{array}[t]{rlll} - x^2+8x+4 &=& 6x +x^2 &\mid\; +x^2 \mid\; -6x \\[5pt] 2x+4 &=& 2x^2 &\mid\; :2 \\[5pt] x+2 &=& x^2 \end{array}$

Einzeichnen der Normalparabel $x^2$ und der Geraden mit der Gleichung $y=x+2$ in ein gemeinsames Koordinatensystem liefert:

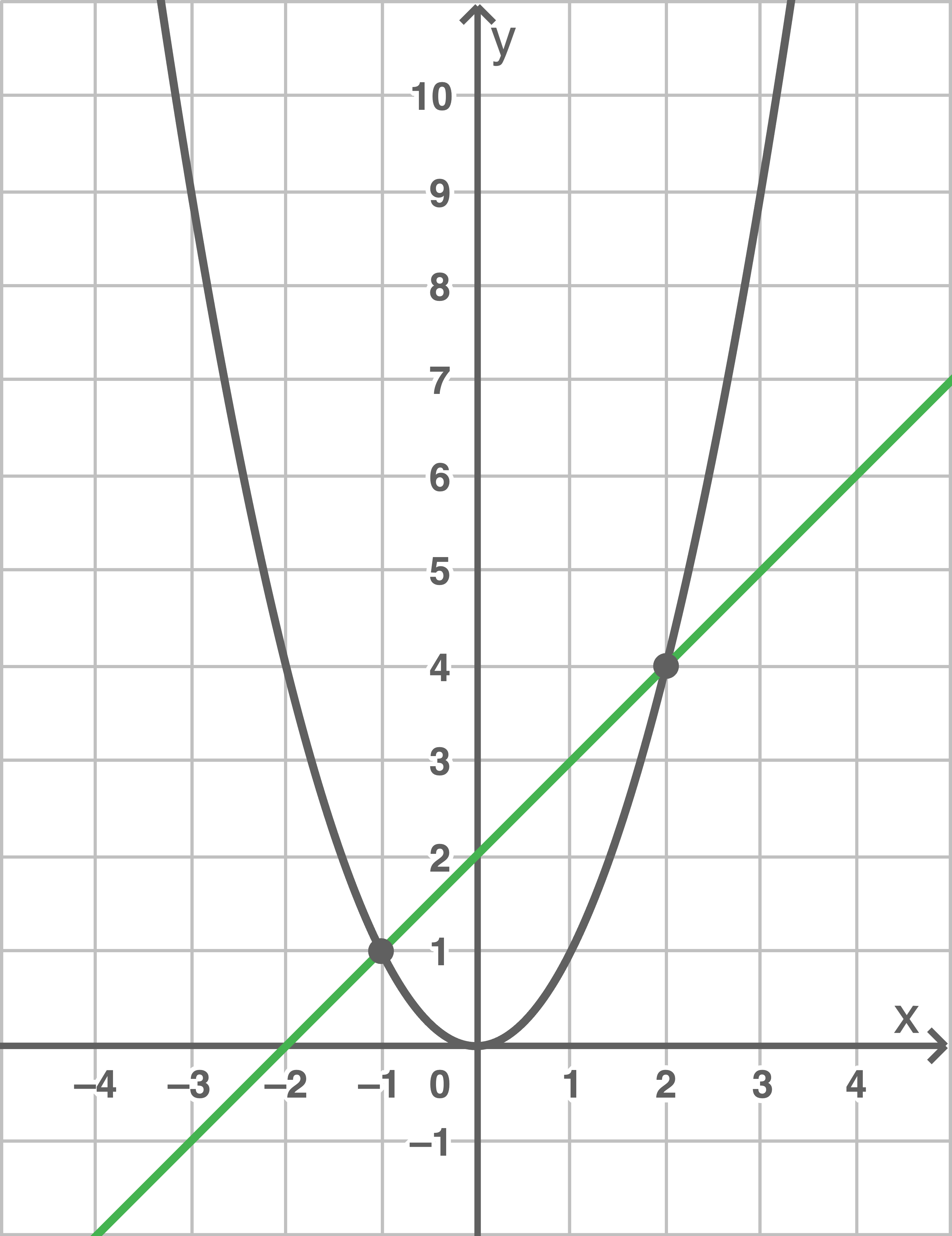Diagramm einer Parabel mit einer Schnittlinie. Koordinatensystem mit Achsen und Gitterlinien.

Die Schnittstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=-1$ und $x_2=2.$

Umformen der Gleichung ergibt:

$\begin{array}[t]{rlll} \dfrac{1}{4} x^2+\dfrac{1}{2} x &=& \dfrac{3}{4} & \; \bigg \vert\, \; -\dfrac{1}{2} x \\[5pt] \dfrac{1}{4} x^2 &=& -\dfrac{1}{2} x+ \dfrac{3}{4} &\; \bigg \vert\, \; \cdot 4 \\[5pt] x^2 &=& -2x+3 \end{array}$

Einzeichnen der Normalparabel $x^2$ und der Geraden mit der Gleichung $y=-2x+3$ in ein gemeinsames Koordinatensystem liefert:

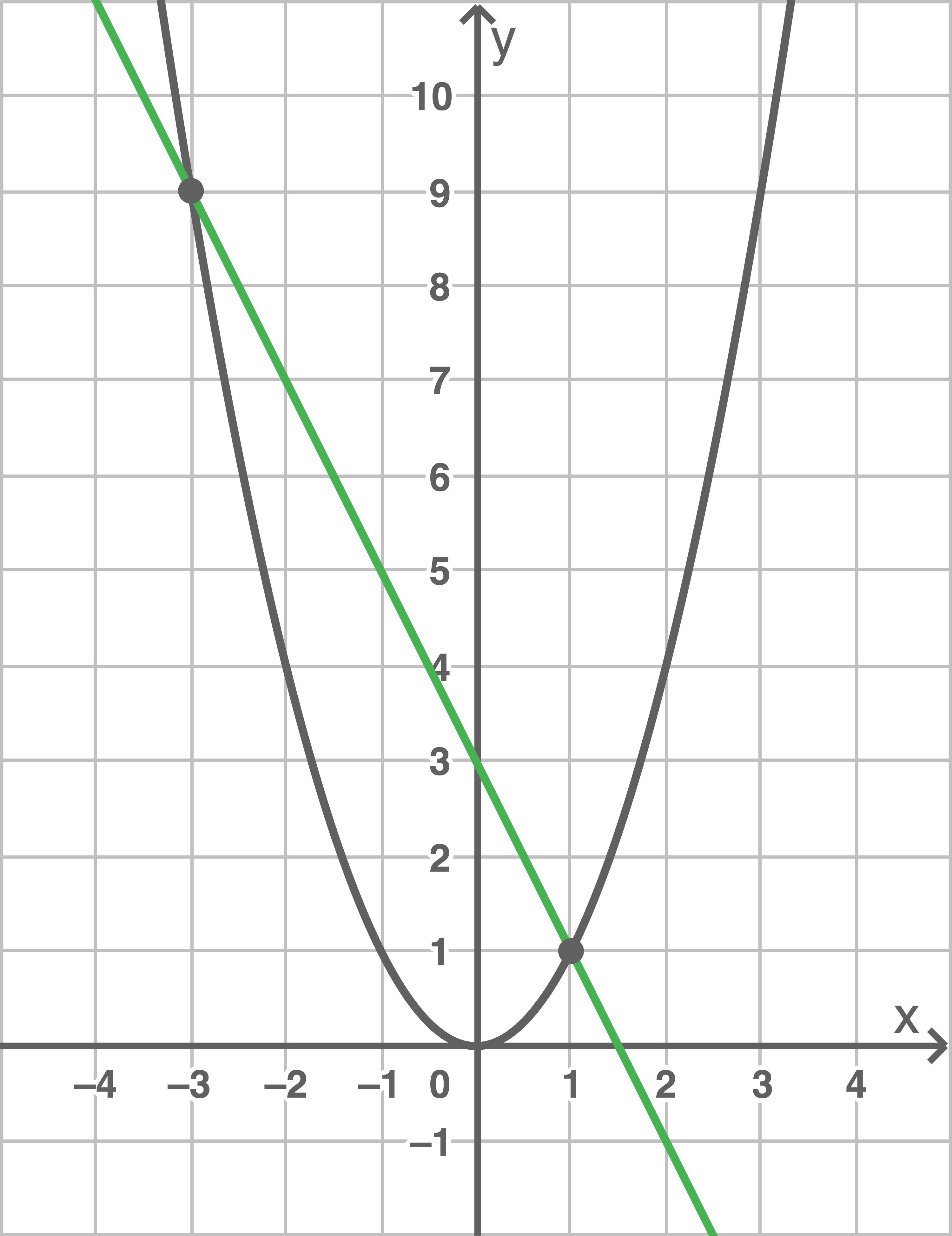Grafik eines Koordinatensystems mit einer Parabel und einer geraden Linie.

Die Schnittstellen entsprechen den Lösungen der Gleichung. Diese sind also gegeben durch $x_1=-3$ und $x_2=1.$

Da $x=5$ eine Lösung der Gleichung ist, muss gelten:

$\begin{array}[t]{rlll} 5^2-6\cdot 5+a&=& 0 & \\[5pt] -5+a&=& 0 &\mid\; +5 \\[5pt] a&=& 5 \end{array}$

Für den Wert $a=5$ hat die Gleichung somit die Lösung $x=5.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?