Aufgabe 1 – Schwingungen
1.
Mit dem Beschleunigungssensor eines Smartphones wird ein  -
- -Diagramm der Bewegung einer Schaukel aufgenommen (siehe Abb. 1).
-Diagramm der Bewegung einer Schaukel aufgenommen (siehe Abb. 1).
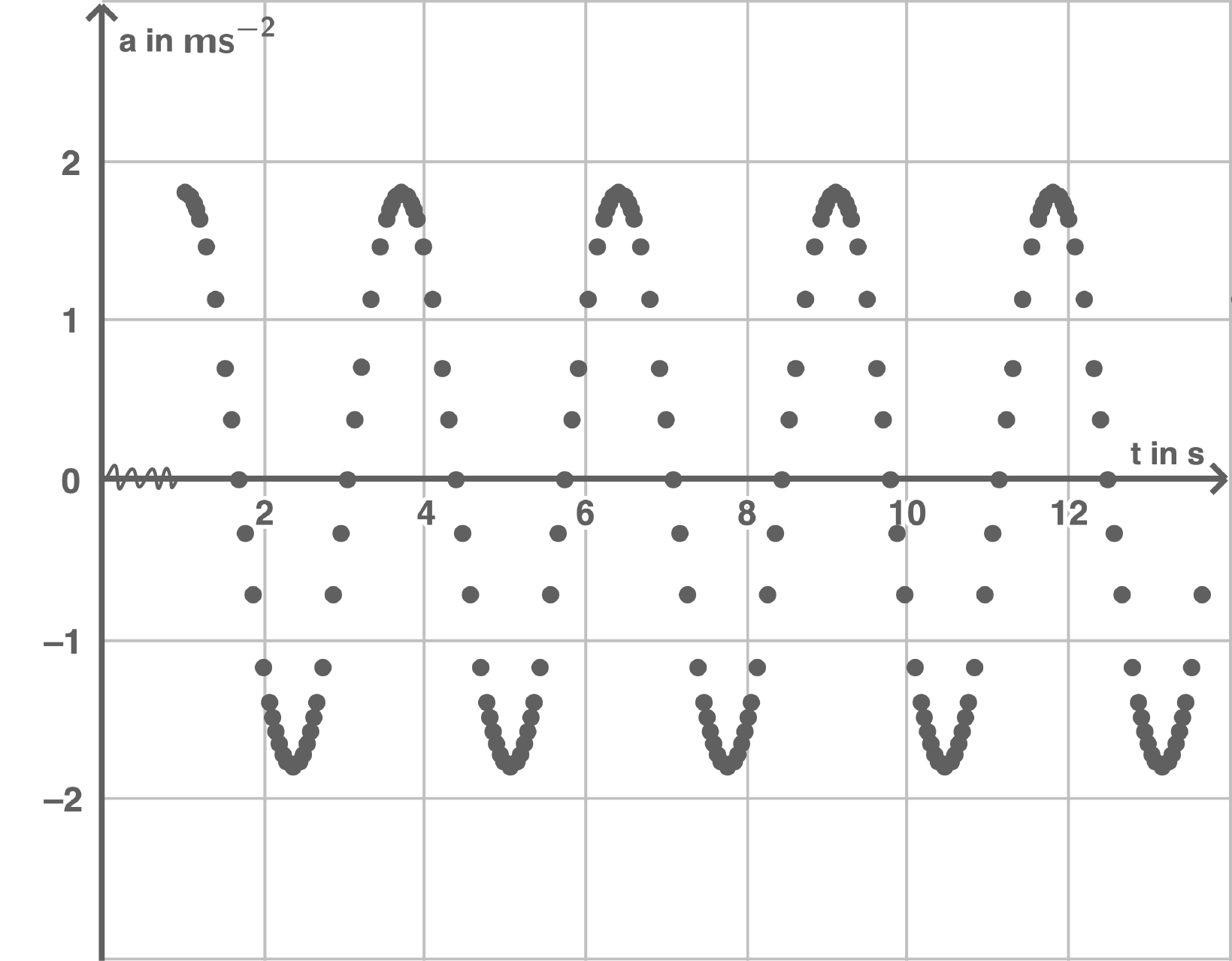 Zur Auswertung werden die aufgenommenen Messwerte durch eine harmonische Schwingung modelliert.
Zur Auswertung werden die aufgenommenen Messwerte durch eine harmonische Schwingung modelliert.
 aus der Ruhelage der Schaukel wird nun verdoppelt und die obige Messung wiederholt. Die Schaukel schwingt nach wie vor harmonisch.
aus der Ruhelage der Schaukel wird nun verdoppelt und die obige Messung wiederholt. Die Schaukel schwingt nach wie vor harmonisch.

Abbildung 1
a)
Bestimme die Periodendauer dieser Schwingung möglichst genau.
(4 BE)
b)
Gib den Zeitpunkt an, zu dem sich die Schaukel zum ersten Mal in der Gleichgewichtslage befindet.
(2 BE)
c)
Zeichne das  -
- -Diagramm für den Zeitraum
-Diagramm für den Zeitraum 
(8 BE)
Die anfängliche Auslenkung
d)
Vergleiche das sich nun ergebende  -
- -Diagramm mit dem Diagramm aus Abbildung 1.
-Diagramm mit dem Diagramm aus Abbildung 1.
(4 BE)
2.
Ein geeignetes Modell für die Schaukel aus Aufgabe 1 ist ein Fadenpendel (siehe Abb. 2). Darunter versteht man einen als punktförmig angenommenen Körper, der an einem Faden der festen Länge  hängt. Die Masse des Fadens und Reibungseffekte werden vernachlässigt.
In Tabelle 1 sind die Beträge des maximalen Auslenkwinkels
hängt. Die Masse des Fadens und Reibungseffekte werden vernachlässigt.
In Tabelle 1 sind die Beträge des maximalen Auslenkwinkels  der zugehörigen Auslenkung
der zugehörigen Auslenkung  und der Rückstellkraft
und der Rückstellkraft  angegeben.
angegeben.
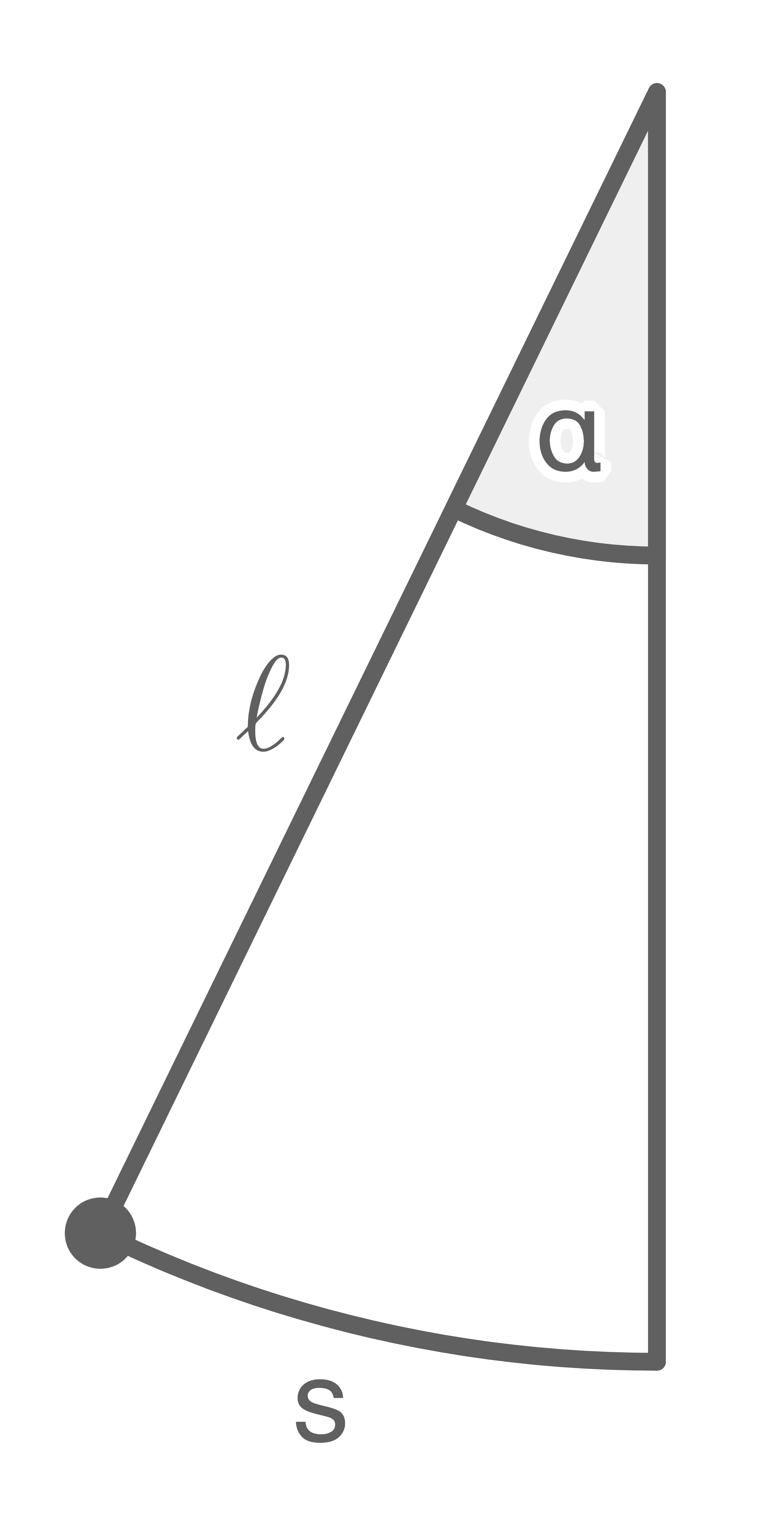
Abbildung 2
| 0 | 0 | 0 |
| 2 | 0,07 | 0,50 |
| 5 | 0,18 | 1,28 |
| 10 | 0,35 | 2,60 |
| 20 | 0,70 | 5,00 |
| 30 | 1,10 | 7,40 |
| 40 | 1,40 | 9,50 |
| 50 | 1,75 | 11,26 |
| 70 | 2,44 | 13,80 |
a)
Bestimme mithilfe eines  -
- -Diagramms den Winkelbereich, in dem näherungsweise eine harmonische Schwingung vorliegt, und bestimme für diesen Bereich einen funktionalen Zusammenhang zwischen
-Diagramms den Winkelbereich, in dem näherungsweise eine harmonische Schwingung vorliegt, und bestimme für diesen Bereich einen funktionalen Zusammenhang zwischen  und
und 
(9 BE)
Im Folgenden wird nur der Bereich betrachtet, in dem das Fadenpendel näherungsweise harmonisch schwingt.
b)
Gib allgemein die Schwingungs-Differentialgleichung eines Fadenpendels für diesen Bereich an und zeige damit, dass  gilt.
gilt.
(6 BE)
c)
Bestimme mithilfe eines geeigneten Messwertepaares die Periodendauer dieses Pendels für die von dir gewählte Auslenkung.
(5 BE)
3.
Während der Untersuchung der Schaukel aus Aufgabe 1 saßen nacheinander mehrere Jugendliche auf der Schaukel und es wurden Messdaten aufgenommen. Hierzu wurde bei gleicher Amplitude der Schaukel jeweils die Zeitspanne  für 10 Perioden gemessen (siehe Tab. 2).
für 10 Perioden gemessen (siehe Tab. 2).
Während der anschließenden Auswertung dieser Daten diskutieren Sandra und Alex. Sandra sagt: „Die Periodendauer verhält sich umgekehrt proportional zur Körpermasse.“
Alex entgegnet: "Es kann keinen Zusammenhang zwischen Körpermasse und Periodendauer geben, da die Masse nicht in der Formel enthalten ist. Die Tendenz in den Messdaten müssen Messfehler sein."
Beurteile die Aussagen von Sandra und Alex.
enthalten ist. Die Tendenz in den Messdaten müssen Messfehler sein."
Beurteile die Aussagen von Sandra und Alex.
| Messung | Körpermasse in kg | |
|---|---|---|
| Hannah | 51 | 28,3 |
| Sandra | 56 | 28,1 |
| Alex | 60 | 28,0 |
| Leon | 65 | 27,6 |
| Max | 70 | 27,4 |
| Marius | 74 | 27,3 |
Alex entgegnet: "Es kann keinen Zusammenhang zwischen Körpermasse und Periodendauer geben, da die Masse nicht in der Formel
(8 BE)
4.
Bei einem Pendel wie in Aufgabe 2 beträgt die Länge  Bei
Bei  unter dem Aufhängepunkt wird ein Stift angebracht. Er hemmt im Punkt
unter dem Aufhängepunkt wird ein Stift angebracht. Er hemmt im Punkt  das Pendel beim Schwingen (siehe Abbildung 3).
Das Pendel wird nun nach rechts um einen Winkel unter
das Pendel beim Schwingen (siehe Abbildung 3).
Das Pendel wird nun nach rechts um einen Winkel unter  aus der Ruhelage ausgelenkt und dann losgelassen.
aus der Ruhelage ausgelenkt und dann losgelassen.
a)
Berechne die Periodendauer dieses sogenannten Hemmungspendels.
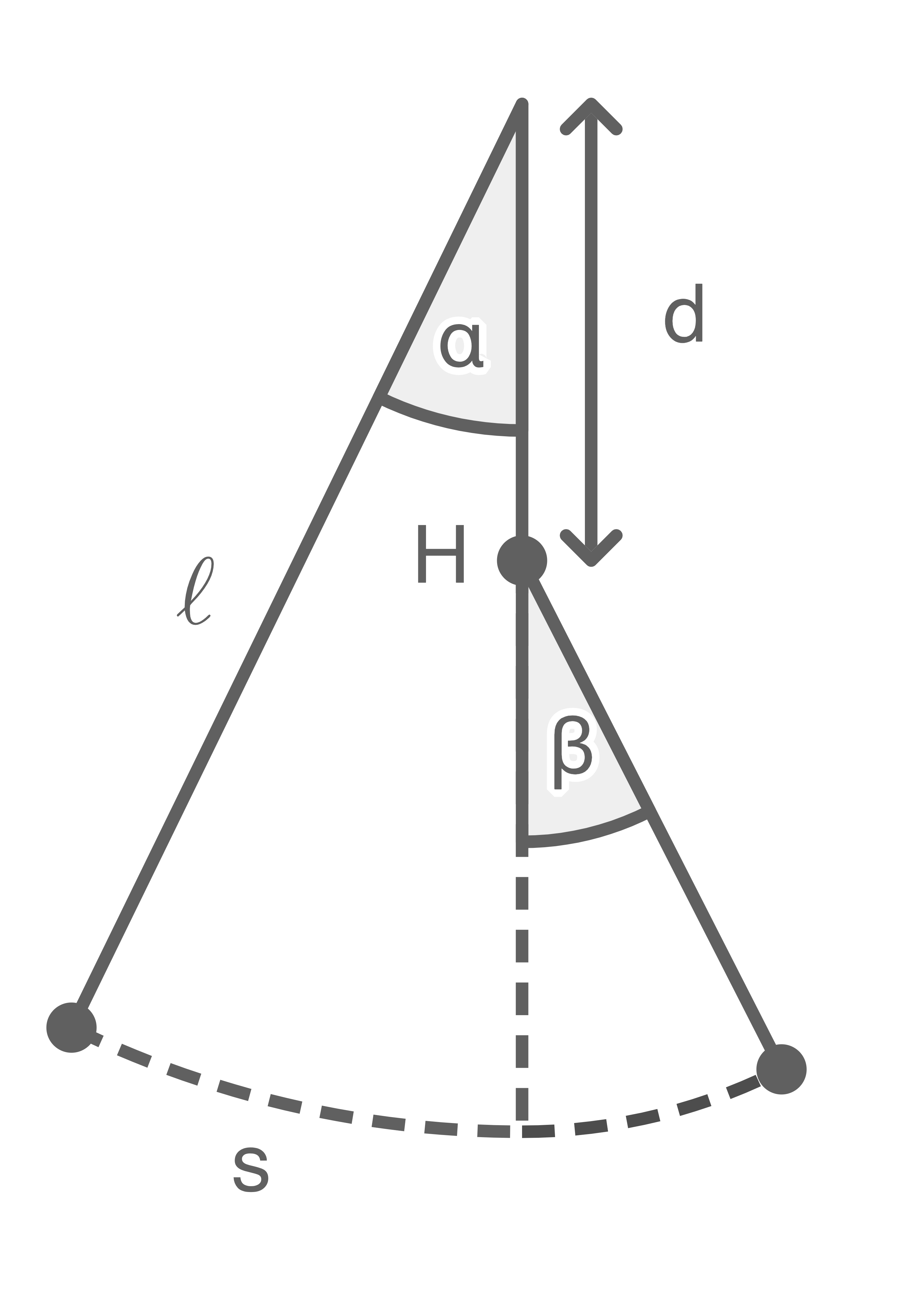
Abbildung 3
(6 BE)
In einem neuen Versuch hat der Pendelkörper eine maximale Geschwindigkeit von
b)
Berechne den maximalen Winkel  den das Pendel im rechten Umkehrpunkt erreicht.
den das Pendel im rechten Umkehrpunkt erreicht.
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Die Periodendauer wird aus Abbildung 1 abgelesen. 4 Perioden haben eine Dauer von  Also ist
Also ist 
b)
Der Zeitpunkt, zu dem sich die Schaukel zum ersten Mal in der Gleichgewichtslage befindet, kann aus der Abbildung 1 abgelesen werden. Der Zeitpunkt entspricht der ersten Schnittstelle mit der  -Achse und ist somit
-Achse und ist somit 
c)
Vorüberlegungen:
Die maximale Beschleunigung kann aus Abbildung 1 abgelesen werden zu  Die Winkelgeschwindigkeit ergibt sich aus:
Die Winkelgeschwindigkeit ergibt sich aus:


 Die Amplitude der Schwingung ergibt sich aus dem Beschleunigung-Zeit-Gesetz zu:
Die Amplitude der Schwingung ergibt sich aus dem Beschleunigung-Zeit-Gesetz zu:
![\(\begin{array}[t]{rll}
\hat{a}&=&\hat{s}\cdot \omega^2 \\[5pt]
\hat{s}&=& \dfrac{\hat{a}}{\omega ^2} \\[5pt]
&=& \dfrac{1,8 \;\frac{\text{m}}{\text{s}^2} }{(2,3\;\frac{1}{\text{s}}) ^2} \\[5pt]
&=& 0,3 \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/0908af270b6a1ba98b6860640ea8848b299e4857f6890b07f5ebb7d64e3b14db_light.svg) Dies entspricht der
Dies entspricht der  -Koordinate des Hochpunktes.
Die Schaukel wird nach
-Koordinate des Hochpunktes.
Die Schaukel wird nach  ausgelenkt.
ausgelenkt.
 -
- -Diagramm
-Diagramm
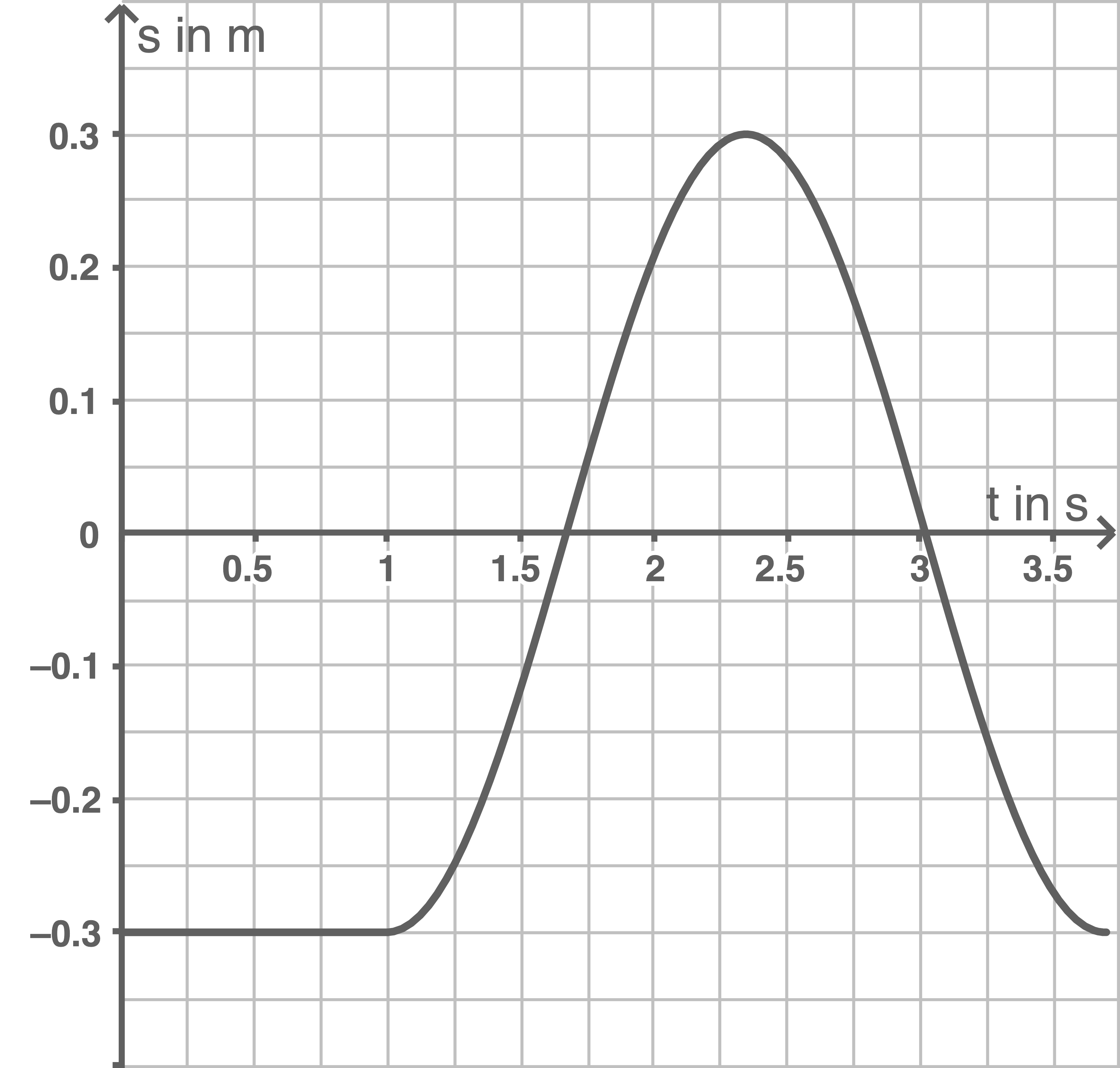

d)
Es ist  Die Auslenkung bei einer harmonischen Schwingung hat keinen Einfluss auf die Periodendauer. Somit wird sie sich nicht verändern. Folglich bleibt auch die Winkelgeschwindigkeit konstant.
Beschleunigung-Zeit-Gesetz:
Die Auslenkung bei einer harmonischen Schwingung hat keinen Einfluss auf die Periodendauer. Somit wird sie sich nicht verändern. Folglich bleibt auch die Winkelgeschwindigkeit konstant.
Beschleunigung-Zeit-Gesetz:  Da auch die Winkelgeschwindigkeit konstant bleibt, ist die maximale Auslenkung proportional zur maximalen Beschleunigung.
Da auch die Winkelgeschwindigkeit konstant bleibt, ist die maximale Auslenkung proportional zur maximalen Beschleunigung.

![\(\begin{array}[t]{rll}
a_{\text{neu}}&=& s_{\text{neu}}\cdot \omega^2 \\[5pt]
a_{\text{neu}}&=& 2\cdot \hat{s}\cdot \omega^2 \\[5pt]
&=&2\cdot \hat{a}
\end{array}\)](https://www.schullv.de/resources/formulas/fd4a36ed971177fec61646686a6784eea8359809c34f644bbb6845c2abae29d8_light.svg) Also wird sich im Diagramm die maximale Beschleunigung verdoppeln.
Also wird sich im Diagramm die maximale Beschleunigung verdoppeln.
2.
a)
1. Schritt:  -
- -Diagramm zeichnen
-Diagramm zeichnen
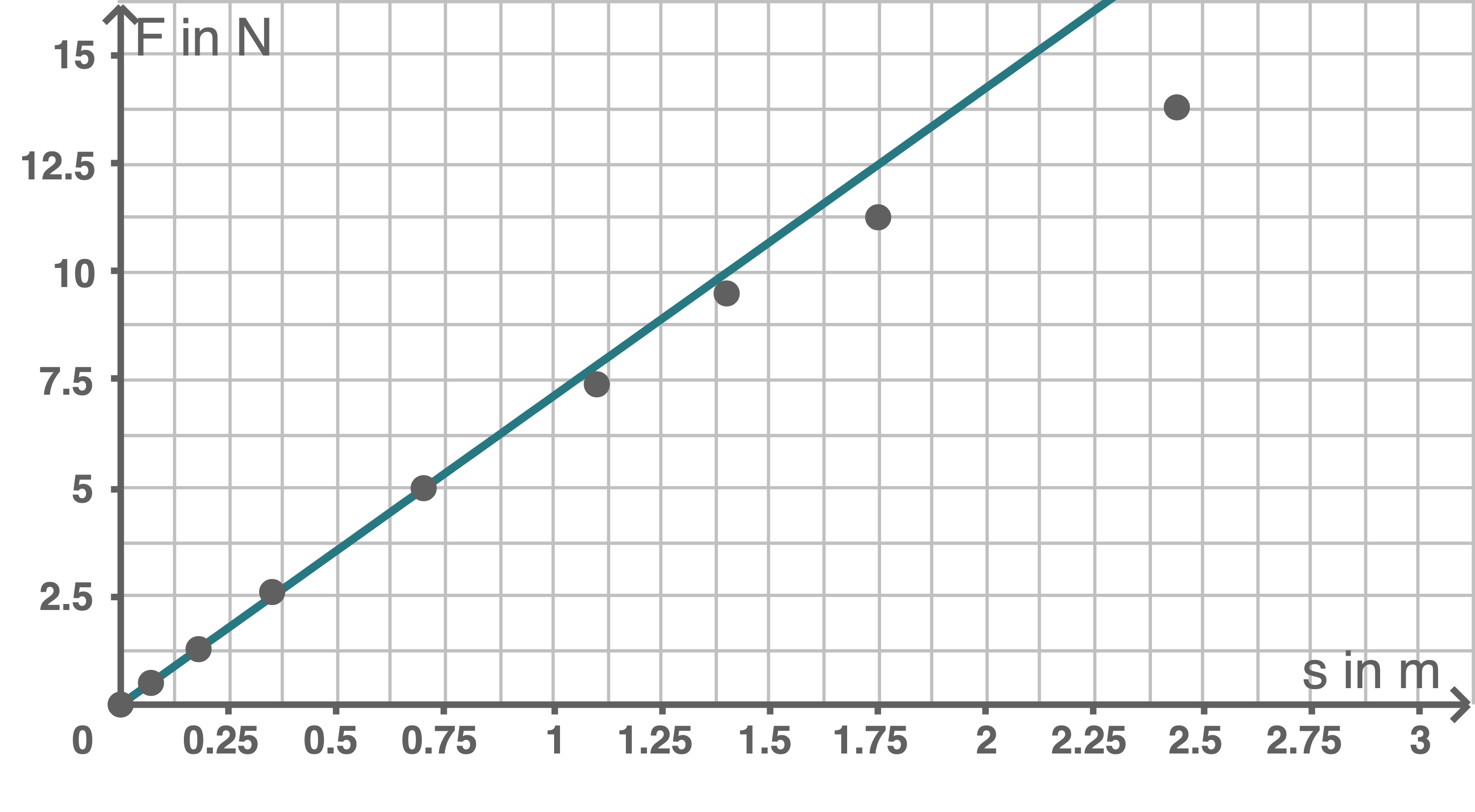 2. Schritt: Winkelbereich in dem harmonischen Schwingung vorliegt
Für kleinere Auslenkungen (bis etwa
2. Schritt: Winkelbereich in dem harmonischen Schwingung vorliegt
Für kleinere Auslenkungen (bis etwa  , was
, was  bis
bis  entspricht) ist der Zusammenhang zwischen
entspricht) ist der Zusammenhang zwischen  und
und  nahezu linear, weswegen hier eine harmonische Schwingung vorliegt.
Bei größeren Auslenkungen (über
nahezu linear, weswegen hier eine harmonische Schwingung vorliegt.
Bei größeren Auslenkungen (über  ) weicht die Rückstellkraft zunehmend von einer linearen Beziehung ab.
3. Schritt: Funktionalen Zusammenhang bestimmen
Es gilt:
) weicht die Rückstellkraft zunehmend von einer linearen Beziehung ab.
3. Schritt: Funktionalen Zusammenhang bestimmen
Es gilt:  Hierbei ist
Hierbei ist  die Proportionalitätskonstante, oft auch Federkonstante genannt.
Um
die Proportionalitätskonstante, oft auch Federkonstante genannt.
Um  zu bestimmen, wird die Steigung der Ausgleichsgeraden bestimmt.
zu bestimmen, wird die Steigung der Ausgleichsgeraden bestimmt.
 Bei
Bei  ist
ist  und die Ausgleichsgerade verläuft durch den Ursprung. Daraus folgt:
und die Ausgleichsgerade verläuft durch den Ursprung. Daraus folgt:

 Der funktionale Zusammenhang lautet folglich:
Der funktionale Zusammenhang lautet folglich: 

b)
Herleitung der Differentialgleichung
2. Newtonsche Axiom:
![\(\begin{array}[t]{rll}
F&=&m\cdot a \\[5pt]
&=& m \cdot \ddot{s}
\end{array}\)](https://www.schullv.de/resources/formulas/f5134aae0668703731b563230b79a8425464d3c6865043ed89ebafd71ba68350_light.svg) Da die Bewegung reibungsfrei verlaufen soll, wirken die Gewichtskraft und die Rückstellkraft. Für die Rückstellkraft gilt:
Da die Bewegung reibungsfrei verlaufen soll, wirken die Gewichtskraft und die Rückstellkraft. Für die Rückstellkraft gilt:
![\(\begin{array}[t]{rll}
F&=& -F_{ G } \cdot \sin (\alpha) \\[5pt]
&=& -F_{ G } \cdot \dfrac{s}{ \ell} \\[5pt]
&=& -m\cdot g \cdot \dfrac{s}{ \ell}
\end{array}\)](https://www.schullv.de/resources/formulas/847a12ffd099acc5e997242def0491bb46d733ecbd6f850c77d7100336de1f6a_light.svg) Die Schwingungs-Differentialgleichung ergibt sich durch Gleichsetzen und Umstellen:
Die Schwingungs-Differentialgleichung ergibt sich durch Gleichsetzen und Umstellen:
![\(\begin{array}[t]{rll}
m\cdot a&=& -m\cdot g \cdot \dfrac{s}{ \ell}&\quad \scriptsize \mid\;:m \\[5pt]
a&=& -g \cdot \dfrac{s}{ \ell} \\[5pt]
a&=& - \dfrac{g}{ \ell} \cdot s \\[5pt]
\ddot{s}(t)&=& - \dfrac{g}{ \ell} \cdot s(t)
\end{array}\)](https://www.schullv.de/resources/formulas/488b88da7ad9a83bb47e7fb8fabd08e99ac6bfe50660ab6c0fe6c58c98f0612a_light.svg) Laut Aufgabenstellung ist nur nach der Angabe der Schwingungs-Differentialgleichung gefragt, somit muss diese nicht zwingend hergeleitet werden.
Mögliche Lösung
Ansatz:
Laut Aufgabenstellung ist nur nach der Angabe der Schwingungs-Differentialgleichung gefragt, somit muss diese nicht zwingend hergeleitet werden.
Mögliche Lösung
Ansatz:  Ableitungen bilden:
Ableitungen bilden:

 Einsetzen des Ansatzes und dessen zweiter Ableitung in die Schwingungs-Differentialgleichung
Die Periodendauer ist damit
Einsetzen des Ansatzes und dessen zweiter Ableitung in die Schwingungs-Differentialgleichung
Die Periodendauer ist damit 
c)
Wenn das Pendel harmonisch schwingt, gilt  Mit dem zweiten Messwertpaar aus Tabelle 1 ergibt sich die Länge des Pendels zu:
Mit dem zweiten Messwertpaar aus Tabelle 1 ergibt sich die Länge des Pendels zu:
 Die Periodendauer ist folglich
Die Periodendauer ist folglich
 .
.
3.
Antiproportionalität prüfen
Die Werte sind nicht konstant, somit ist Sandras Aussage falsch.
Alex Aussage:
Diese Formel für die Periodendauer ist in dieser Situation nicht anwendbar, da sie auf dem Modell des Fadenpendels bei kleinen Auslenkungen beruht. Damit ist die erste Aussage zur Massenabhängigkeit der Periodendauer nicht richtig. Es kann nicht zwingend gefolgert werden, dass in diesem Experiment kein Zusammenhang zwischen der Masse und der Periodendauer besteht. Die Tendenz in den Messdaten muss sich also nicht durch Messfehler ergeben.
| Messung | |
|---|---|
| Hannah | 144 |
| Sandra | 157 |
| Alex | 168 |
| Leon | 179 |
| Max | 192 |
| Marius | 202 |
4.
a)
Gegeben: 

 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
T_{\text {links }}&=& 2 \cdot \pi \cdot \sqrt{\dfrac{\ell}{g}} \\[5pt]
&=& 2 \cdot \pi \cdot \sqrt{\dfrac{2,0 \;\text{m} }{9,81 \frac{\text{m}}{\text{s}^2}}} \\[5pt]
&=&2,8\;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/0bf35d2e0adf9fcf669edf5faa62141fbda063d8d44c9a95d96198434fc46042_light.svg)
![\(\begin{array}[t]{rll}
T_{\text {rechts }}&=& 2 \cdot \pi \cdot \sqrt{\dfrac{\ell-d}{g}} \\[5pt]
&=& 2 \cdot \pi \cdot \sqrt{\dfrac{1,6 \;\text{m} }{9,81 \frac{\text{m}}{\text{s}^2}}} \\[5pt]
&=& 2,5 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/c2f57c63679a8cd621af86cdef66099d68a4abb855b8a3568d3f9bb8aeb2702b_light.svg) Damit ist:
Damit ist:

b)
Gegeben:  Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
E_{\text{kin}}&=& E_{\text{pot}} \\[5pt]
\dfrac{1}{2} \cdot m \cdot v^2 &=& m \cdot g \cdot h &\quad \scriptsize \mid\;\cdot \dfrac{1}{m \cdot g} \\[5pt]
\dfrac{m\cdot v^2}{2 \cdot m\cdot g}&=& h \\[5pt]
h &=& \dfrac{m\cdot v^2}{2 \cdot m\cdot g} \\[5pt]
h &=& \dfrac{v^2}{2 \cdot g} \\[5pt]
&=& \dfrac{1\;\frac{\text{m}}{\text{s}}}{2 \cdot 9,81 \;\frac{\text{m}}{\text{s}^2}} \\[5pt]
&=& 5,1 \;\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/0aeba7cdf9367e5eb80d2019b130b3988883585f9d131321e91ec80490afa7bb_light.svg) Mit
Mit  ergibt sich
ergibt sich 