Aufgabe 3 – Elektromagnetismus
1.
Die kreisförmigen Platten eines luftgefüllten Kondensators haben einen Durchmesser von  und einen Abstand von
und einen Abstand von  Der Kondensator ist mit einem Netzgerät verbunden, das eine Gleichspannung von
Der Kondensator ist mit einem Netzgerät verbunden, das eine Gleichspannung von  erzeugt.
erzeugt.
 des Kondensators in Abhängigkeit vom Plattenabstand
des Kondensators in Abhängigkeit vom Plattenabstand  untersucht. Vor jeder Ladungsmessung wird ein Plattenabstand
untersucht. Vor jeder Ladungsmessung wird ein Plattenabstand  eingestellt und der Raum zwischen den Platten vollständig mit dem gleichen dielektrischen Material ausgefüllt. Danach wird an den Kondensator eine Spannung von
eingestellt und der Raum zwischen den Platten vollständig mit dem gleichen dielektrischen Material ausgefüllt. Danach wird an den Kondensator eine Spannung von  angelegt. Nach dem Aufladevorgang wird der Kondensator von der Spannungsquelle getrennt und die Ladung
angelegt. Nach dem Aufladevorgang wird der Kondensator von der Spannungsquelle getrennt und die Ladung  gemessen. Die Tabelle zeigt die Ergebnisse dieser Versuchsreihe.
gemessen. Die Tabelle zeigt die Ergebnisse dieser Versuchsreihe.
a)
Berechne die elektrische Feldstärke im Kondensator.
b)
Berechne die Kapazität des Kondensators.
Nun wird der geladene Kondensator vom Netzgerät getrennt und anschließend der Plattenabstand vergrößert.
c)
Erkläre, wie sich dies auf die Kapazität und die elektrische Feldstärke auswirkt.
In einer Versuchsreihe wird die Ladung | 4,0 | 4,4 |
| 3,0 | 5,7 |
| 2,0 | 8,7 |
| 1,0 | 17,4 |
d)
Ermittle anhand der Messwerte einen Zusammenhang zwischen den Größen  und
und 
e)
Bestimme unter Berücksichtigung aller Messwerte die relative Permittivität  des dielektrischen Materials.
des dielektrischen Materials.
(8 VP)
2.
Eine langgestreckte Spule mit Eisenkern hat 1200 Windungen, eine Länge von  und eine Querschnittsfläche von
und eine Querschnittsfläche von  Die Spule hat eine Induktivität von
Die Spule hat eine Induktivität von  und einen ohmschen Widerstand von
und einen ohmschen Widerstand von 
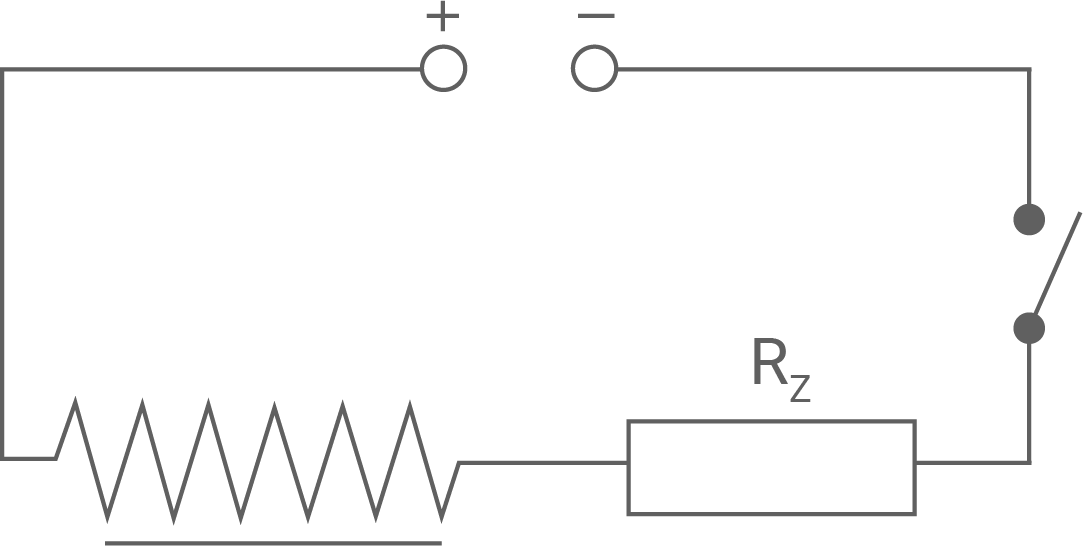
 mit einem Netzgerät verbunden (siehe Abbildung 1). Zum Zeitpunkt
mit einem Netzgerät verbunden (siehe Abbildung 1). Zum Zeitpunkt  wird der Stromkreis durch einen Schalter geschlossen.
wird der Stromkreis durch einen Schalter geschlossen.
 Bei der verwendeten Spule beträgt die maximal zulässige Stromstärke
Bei der verwendeten Spule beträgt die maximal zulässige Stromstärke 
 nun einen Wert von
nun einen Wert von  weiterhin beträgt
weiterhin beträgt  Für den zeitlichen Verlauf der Stromstärke beim Einschaltvorgang einer Spule gilt:
Für den zeitlichen Verlauf der Stromstärke beim Einschaltvorgang einer Spule gilt:
 ,
wobei
,
wobei  der ohmsche Gesamtwiderstand der Schaltung ist.
der ohmsche Gesamtwiderstand der Schaltung ist.
a)
Berechne die Permeabilitätszahl  des Eisenkerns.
des Eisenkerns.
Die Spule wird über einen zusätzlichen ohmschen Widerstand 
Abbildung 1
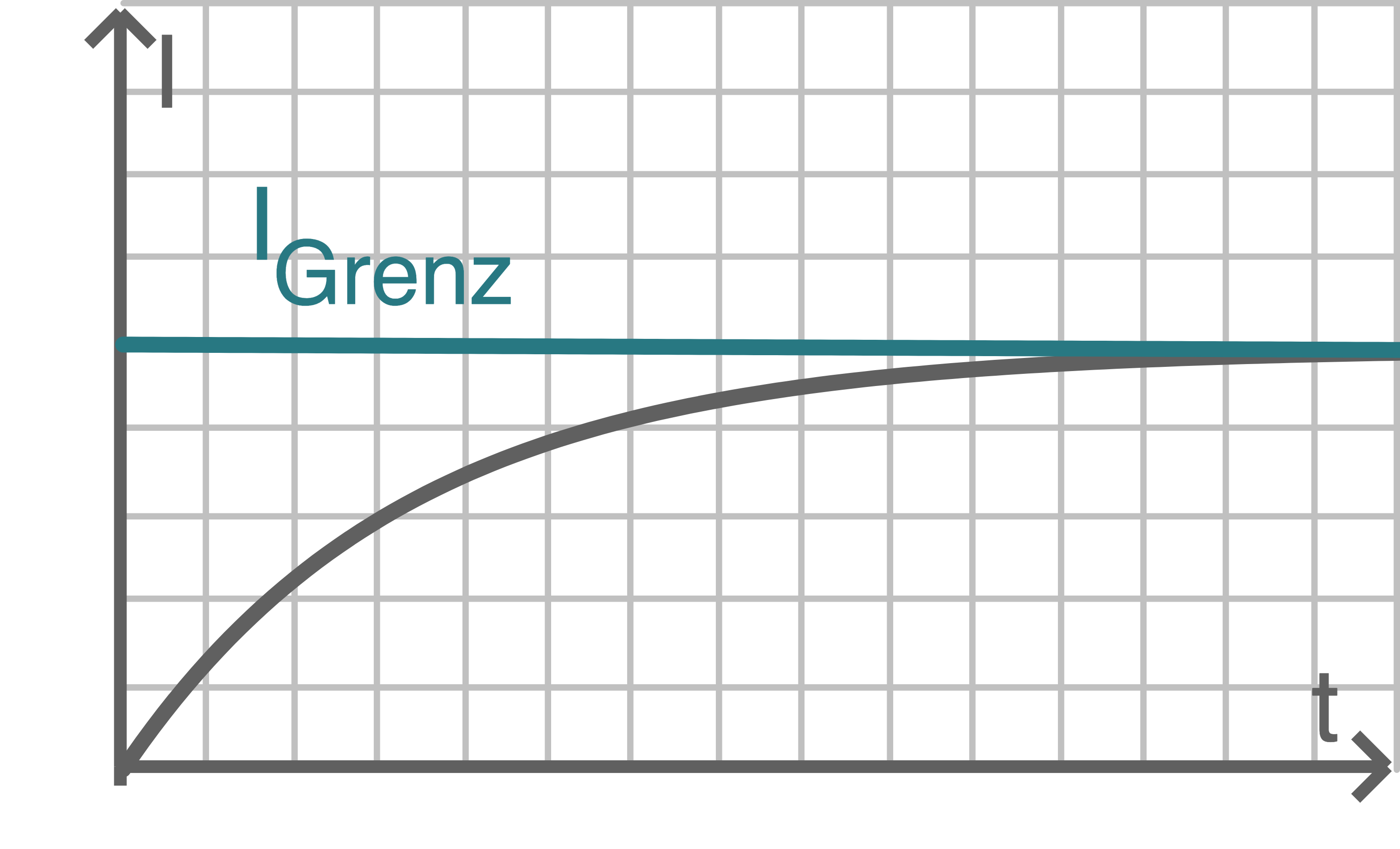
b)
Skizziere den zeitlichen Verlauf der Stromstärke nach dem Schließen des Schalters und erläutere den Kurvenverlauf.
Die Spannung am Netzgerät beträgt
c)
Zeige, dass dazu der Widerstand  mindestens einen Wert von
mindestens einen Wert von  haben muss.
haben muss.
In der Schaltung von Abbildung 1 hat
d)
Berechne die Stromstärke in der Spule zum Zeitpunkt  nach dem Einschalten.
nach dem Einschalten.
e)
Erläutere, wie sich die in Aufgabenteil d) berechnete Stromstärke zum Zeitpunkt  ändert, wenn man
ändert, wenn man
(i)
einen Eisenkern mit einer kleineren Permeabilitätszahl verwendet.
(ii)
nur  vergrößert.
vergrößert.
(10 VP)
3.
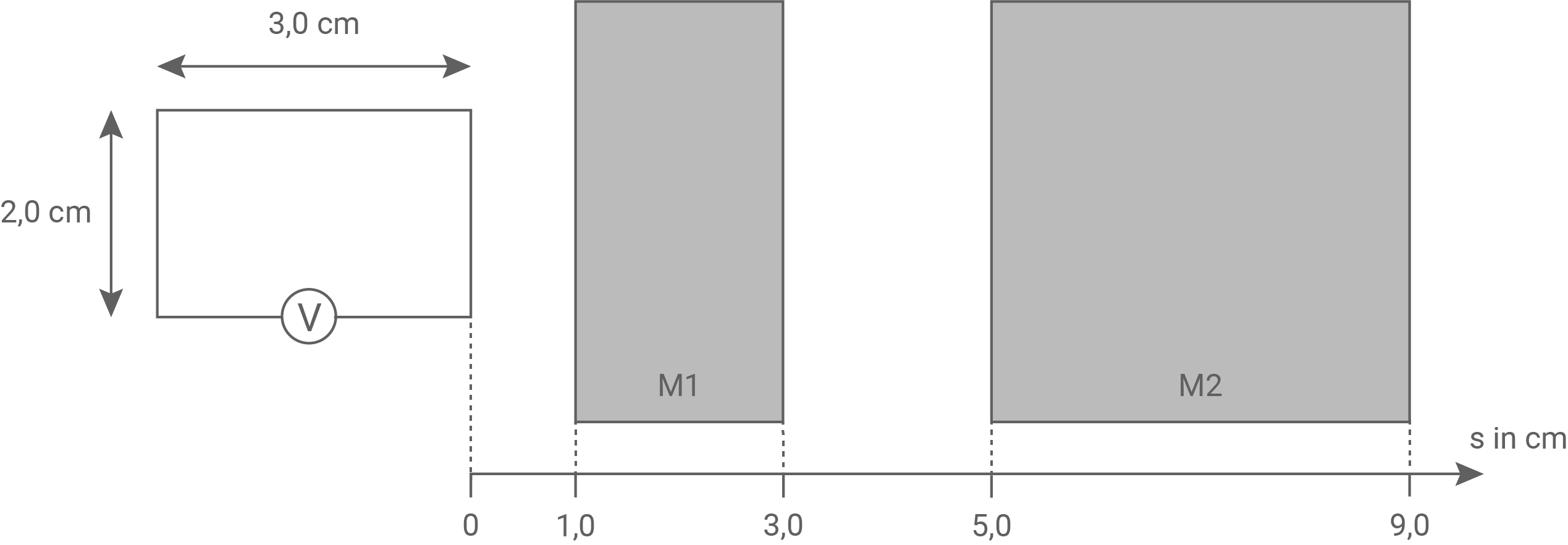
In der Versuchsanordnung nach Abbildung 2 befindet sich auf der linken Seite ein rechteckiger Leiterrahmen, dessen Anschlüsse mit einem hochohmigen Voltmeter verbunden sind. Rechts daneben befinden sich zwei räumlich begrenzte homogene Magnetfelder M1 und M2.
 In einem ersten Versuch ist die magnetische Flussdichte in beiden Magnetfeldern aus der Zeichenebene senkrecht heraus gerichtet und hat einen Betrag von
In einem ersten Versuch ist die magnetische Flussdichte in beiden Magnetfeldern aus der Zeichenebene senkrecht heraus gerichtet und hat einen Betrag von  Der Leiterrahmen wird mit der konstanten Geschwindigkeit
Der Leiterrahmen wird mit der konstanten Geschwindigkeit  senkrecht zu den Feldlinien nach rechts bewegt. Er befindet sich zum Zeitpunkt
senkrecht zu den Feldlinien nach rechts bewegt. Er befindet sich zum Zeitpunkt  an der abgebildeten Position (siehe Abbildung 2).
an der abgebildeten Position (siehe Abbildung 2).


Abbildung 2
a)
Erkläre, warum während des Eintauchens des Leiterrahmens in das Magnetfeld M1 eine Spannung angezeigt wird und berechne deren Wert.
b)
Zeichne das Zeit-Spannungs-Diagramm für die Bewegung des Leiterrahmens von  bis zu dem Zeitpunkt, an dem dieser vollständig in das rechte Magnetfeld M2 eingetaucht ist.
bis zu dem Zeitpunkt, an dem dieser vollständig in das rechte Magnetfeld M2 eingetaucht ist.
In einem neuen Versuch befindet sich der Leiterrahmen vollständig im Bereich des Feldes M2 und ruht. Das senkrecht zur Zeichenebene gerichtete Magnetfeld M2 besitzt nun eine zeitlich veränderliche Flussdichte
c)
Ermittle den Wert für  bei dem die induzierte Spannung den Maximalwert
bei dem die induzierte Spannung den Maximalwert  hat.
hat.
(8 VP)
4.
Ein Stabmagnet ist an einer Spiralfeder aufgehängt und kann in vertikaler Richtung reibungsfrei schwingen. Unterhalb des Magneten befindet sich ein fest angebrachter Aluminiumring (siehe Abbildung 3). Bei Annäherung des Stabmagneten an den Ring wird im Ring ein elektrischer Strom induziert, wobei sich die Elektronen in der in Abbildung 3 eingezeichneten Richtung bewegen.
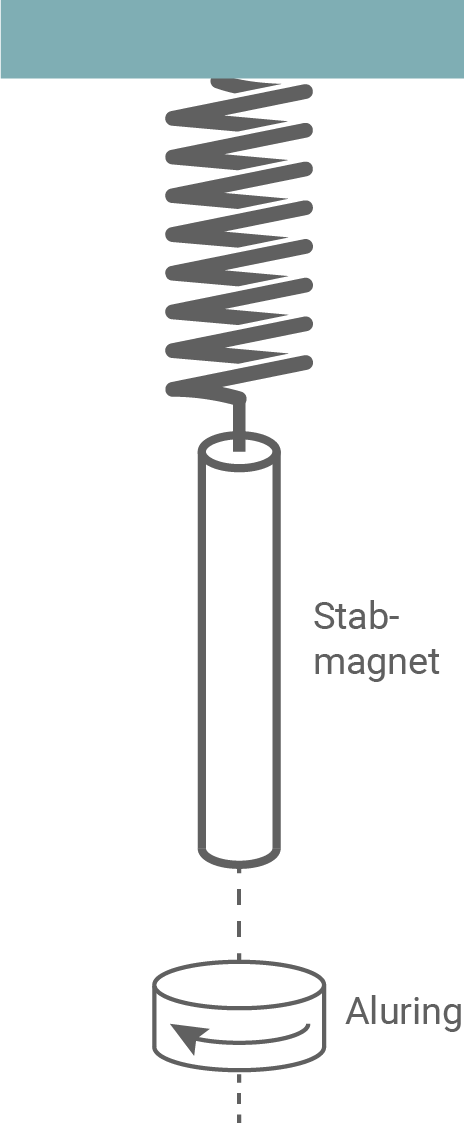

Abbildung 3
a)
Ermittle die hierzu nötige Polung des Stabmagneten.
In einem weiteren Versuch wird über mehrere Periodendauern die Schwingung des Stabmagneten mit und ohne Aluminiumring beobachtet.
b)
Erläutere, worin sich die beiden Schwingungen unterscheiden.
(4 VP)
1
a)
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
E&=&\dfrac{U}{d} \\[5pt]
&=&\dfrac{3000 \mathrm{~V}}{4,0 \cdot 10^{-3} \mathrm{~m}} \\[5pt]
&=& 7,5 \cdot 10^{5} ~\frac{\text{V}}{\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/c53ef77f77618fd162ded7badfc874a84a0749b93520f10f0200d29fbc077690_light.svg)
b)
c)
Es ist 
 somit verkleinert sich die Kapazität des Kondensators, wenn sich der Plattenabstand vergrößert.
Es gilt
somit verkleinert sich die Kapazität des Kondensators, wenn sich der Plattenabstand vergrößert.
Es gilt  und daraus folgt:
und daraus folgt:
![\(\begin{array}[t]{rll}
E&=& \dfrac{U}{d}&\quad \scriptsize \mid\;d=\varepsilon_{0} \cdot \varepsilon_{\mathrm{r}} \cdot \dfrac{A}{C} \\[5pt]
&=&\dfrac{Q}{C}\cdot \dfrac{1}{\varepsilon_{0} \cdot \varepsilon_{\mathrm{r}}} \cdot \dfrac{C}{A} \\[5pt]
&=& \dfrac{1}{\varepsilon_{0} \cdot \varepsilon_{\mathrm{r}}} \cdot \dfrac{Q}{A}
\end{array}\)](https://www.schullv.de/resources/formulas/a1344666f3b146fa44e8a2d96b789d3607d16bf29501242c80a4c0a9aabd70ed_light.svg) Die Feldstärke des Kondensators bleibt gleich. Wenn die Spannungsquelle abgetrennt ist, bleibt die Ladungsmenge auf der Platte beim Auseinanderziehen konstant und die Elektrische Feldstärke
Die Feldstärke des Kondensators bleibt gleich. Wenn die Spannungsquelle abgetrennt ist, bleibt die Ladungsmenge auf der Platte beim Auseinanderziehen konstant und die Elektrische Feldstärke  verändert sich nach der Formel nur, wenn
verändert sich nach der Formel nur, wenn  oder
oder  sich verändern.
sich verändern.
d)
In der Tabelle kann ablesen werden, dass die aufgenommene Ladung  bei kleiner werdendem Abstand
bei kleiner werdendem Abstand  zunimmt. Naheliegend ist die Vermutung, dass
zunimmt. Naheliegend ist die Vermutung, dass  und
und  umgekehrt proportionale Größen sein könnten. In diesem Fall muss das Produkt
umgekehrt proportionale Größen sein könnten. In diesem Fall muss das Produkt  konstant sein.
konstant sein.
Das Produkt ist annähernd konstant und deshalb gilt:  Es gilt:
Es gilt:  .
.
| 4,0 | 4,4 | 17,6 |
| 3,0 | 5,7 | 17,1 |
| 2,0 | 8,7 | 17,4 |
| 1,0 | 17,4 | 17,4 |
e)
Die Formel für die Kapazität eines Kondensators lautet:  Somit ergibt sich:
Somit ergibt sich:

2
a)
b)
c)
Für die zulässige Stromstärke ( ) in der Spule gilt:
) in der Spule gilt:
![\(\begin{array}[t]{rll}
I_{\text{max}} & \geq & \dfrac{U}{R_\text{ges}} &\quad \scriptsize \mid\; \cdot \dfrac{R_\text{ges}}{I_{\text{max}}} \\[5pt]
R_\text{ges} & \geq & \dfrac{U}{I_{\text{max}}} \\[5pt]
R_\text{ges} & \geq & \dfrac{12 \mathrm{~V}}{0,8 \mathrm{~A}} \\[5pt]
R_\text{ges} & \geq & 15 ~\Omega
\end{array}\)](https://www.schullv.de/resources/formulas/90ca205f510464f81b595f21138bc5bcada705b945b24fe21f33b866e8791e00_light.svg) Der Widerstand der Spule
Der Widerstand der Spule  beträgt nach Aufgabenstellung
beträgt nach Aufgabenstellung  Da es sich um eine Reihenschaltung handelt gilt für die Widerstände:
Da es sich um eine Reihenschaltung handelt gilt für die Widerstände:
![\(\begin{array}[t]{rll}
R_\text{ges} &=& R_\text{sp} + R_\text{z} &\quad \scriptsize \mid\; - R_\text{Sp} \\[5pt]
R_\text{ges} - R_\text{sp} &=& R_\text{z} \\[5pt]
15 ~\Omega - 5 ~\Omega &=& R_\text{z}
\\[5pt]
10 ~\Omega &=& R_\text{z}
\end{array}\)](https://www.schullv.de/resources/formulas/8504f846eb6d838e70959ae65f06b16b342d5ee3090ecec568efdc67cf5b79c3_light.svg) Der erforderliche Zusatzwiderstand
Der erforderliche Zusatzwiderstand  muss mindestens
muss mindestens  betragen.
betragen.
d)
Mit der angegebenen Gleichung für die Stromstärke in der Spule ergibt sich durch Einsetzen:



e)
(i)
Durch die Verkleinerung der Permeabilität verringert sich die Induktivität der Spule, da  Der ohmische Widerstand wird durch die Veränderung der Permeabilität nicht beeinflusst.
Wird nun die Gleichung der Stromstärke
Der ohmische Widerstand wird durch die Veränderung der Permeabilität nicht beeinflusst.
Wird nun die Gleichung der Stromstärke 
 betrachtet ist erkennbar, dass
betrachtet ist erkennbar, dass  für eine geringere Induktivität größer wird. Durch die Verringerung von
für eine geringere Induktivität größer wird. Durch die Verringerung von  wird der Faktor
wird der Faktor  kleiner und somit steigt die Stromstärke an.
kleiner und somit steigt die Stromstärke an.
(ii)
Da  gilt, nimmt bei einer Erhöhung von
gilt, nimmt bei einer Erhöhung von  auch
auch  zu und somit nimmt die maximale Stromstärke ab, da
zu und somit nimmt die maximale Stromstärke ab, da  Außerdem ist der Anstieg der Stromstärke geringer, da
Außerdem ist der Anstieg der Stromstärke geringer, da 
 geringer wird, wenn sich
geringer wird, wenn sich  erhöht.
Somit verringert sich
erhöht.
Somit verringert sich  bei einer Erhöhung des Widerstands
bei einer Erhöhung des Widerstands 
3
a)
Während des Eintauchens nimmt der magnetische Fluss durch die Fläche des Leiterrahmens zu, da der vom Magnetfeld durchsetzte Flächenanteil beim Eintauchen größer wird. Aufgrund der Änderung des magnetischen Flusses wird eine Spannung im Leiter induziert.
Induktionsspannung beim Feldeintritt mit der allgemeinen Formel und den gegebenen Werten:
![\(\begin{array}[t]{rll}
U_{\text {ind }} &=& B \cdot d \cdot v \\[5pt]
U_{\text {ind }} &=& 0,35 \mathrm{~T} \cdot 0,02 \mathrm{~m} \cdot 0,01 \mathrm{~ms}^{-1} \\[5pt]
U_{\text {ind }} &=& 70 ~ \mathrm{\mu V}
\end{array}\)](https://www.schullv.de/resources/formulas/fa0bd3950dd5af1e1ba6805c575eeebca5a643f4eb9c1de6092e55eaf6abbdd8_light.svg)
b)
Mit  dauert es eine Sekunde, bis der Leiterrahmen den Feldbereich M1 erreicht. In den Intervallen [3s, 4s] und [5s, 6s] wird insgesamt keine Spannung induziert, da keine Flussänderung durch die Leiterschleife vorliegt. Nach 8s ist der Rahmen erstmals vollständig in den Feldbereich M2 eingetaucht. Es ergibt sich das folgende Schaubild:
dauert es eine Sekunde, bis der Leiterrahmen den Feldbereich M1 erreicht. In den Intervallen [3s, 4s] und [5s, 6s] wird insgesamt keine Spannung induziert, da keine Flussänderung durch die Leiterschleife vorliegt. Nach 8s ist der Rahmen erstmals vollständig in den Feldbereich M2 eingetaucht. Es ergibt sich das folgende Schaubild:
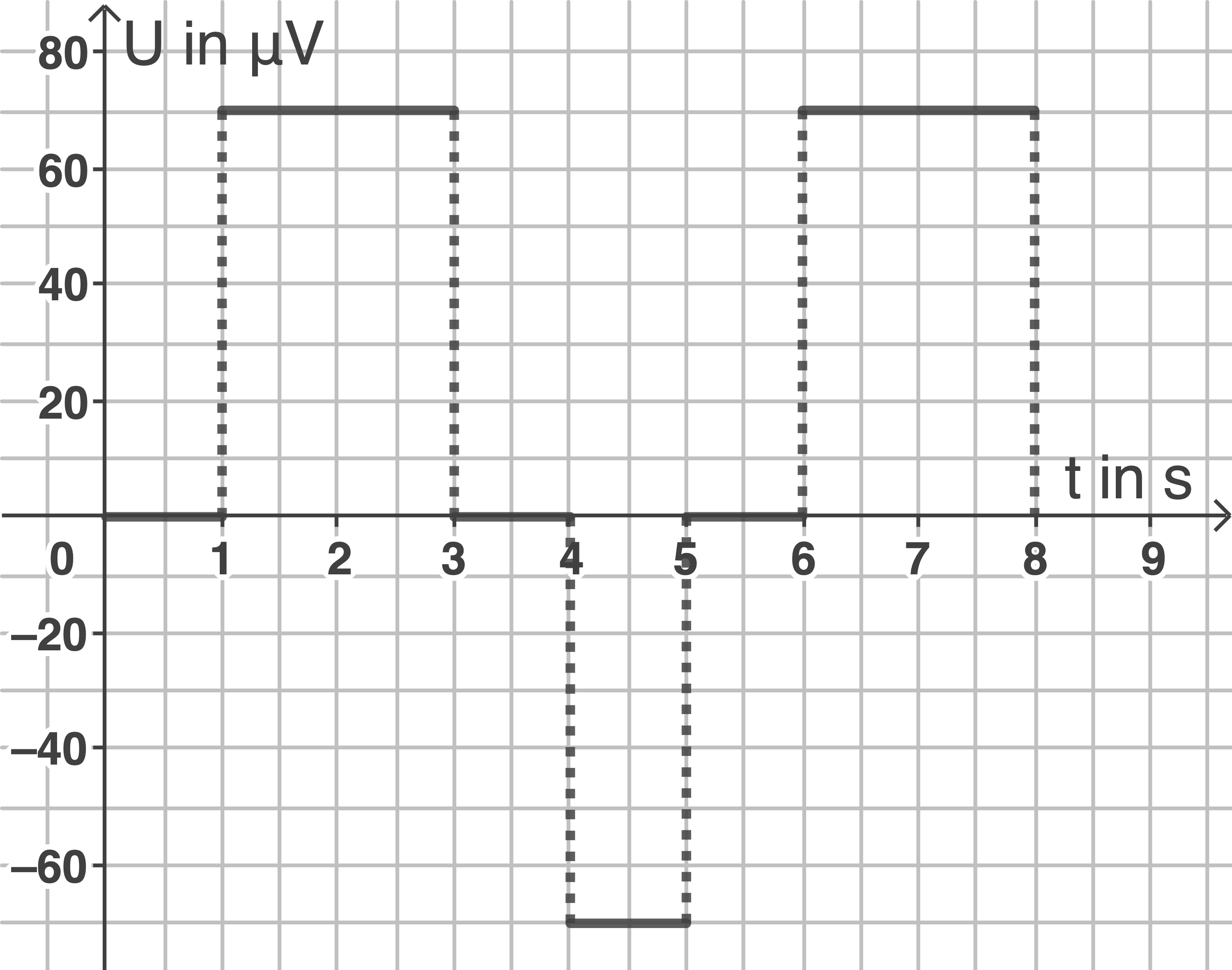

c)
Für die Induktionsspannung gilt hier: 
 .
Aus der Aufgabenstellung ergibt sich die Formel
.
Aus der Aufgabenstellung ergibt sich die Formel  mit
mit  . Wird
. Wird  abgeleitet, ergibt sich:
abgeleitet, ergibt sich: 
 Einsetzen ergibt:
Einsetzen ergibt: 
 Die Spannung wird maximal für
Die Spannung wird maximal für  Somit ergibt sich folgende Gleichung:
Somit ergibt sich folgende Gleichung:

4
a)
Wenn die Elektronen sich wie im Bild eingezeichnet bewegen, erzeugt der im Ring induzierte Strom ein Magnetfeld, das im Inneren des Aluminiumrings nach oben gerichtet ist (Linke-Faust-Regel). Nach dem Induktionsgesetz ist das magnetische Feld des Rings dem Feld des sich annähernden Stabmagneten entgegengerichtet. Am unteren Ende des Stabmagneten befindet sich somit sein Nordpol.
b)
Ohne Aluminiumring führt der reibungsfrei schwingende Stabmagnet eine ungedämpfte Schwingung aus. Die Schwingung bei Anwesenheit des Metallrings erfolgt gedämpft: Die Energie des schwingenden Systems aus Feder und Stabmagnet geht nach und nach in das elektromagnetische Feld des Metallrings über.