Aufgabe 1 – Mechanische Schwingungen
1.
Abbildung 1 a zeigt die Schaukelbewegung eines Kindes. Diese wurde gefilmt und mit einem Videoanalyseprogramm wurde ein Zeit-Auslenkung-Diagramm erstellt (siehe Abbildung 1 b). Dieses zeigt, dass die Bewegung näherungsweise als harmonische Schwingung betrachtet werden kann.

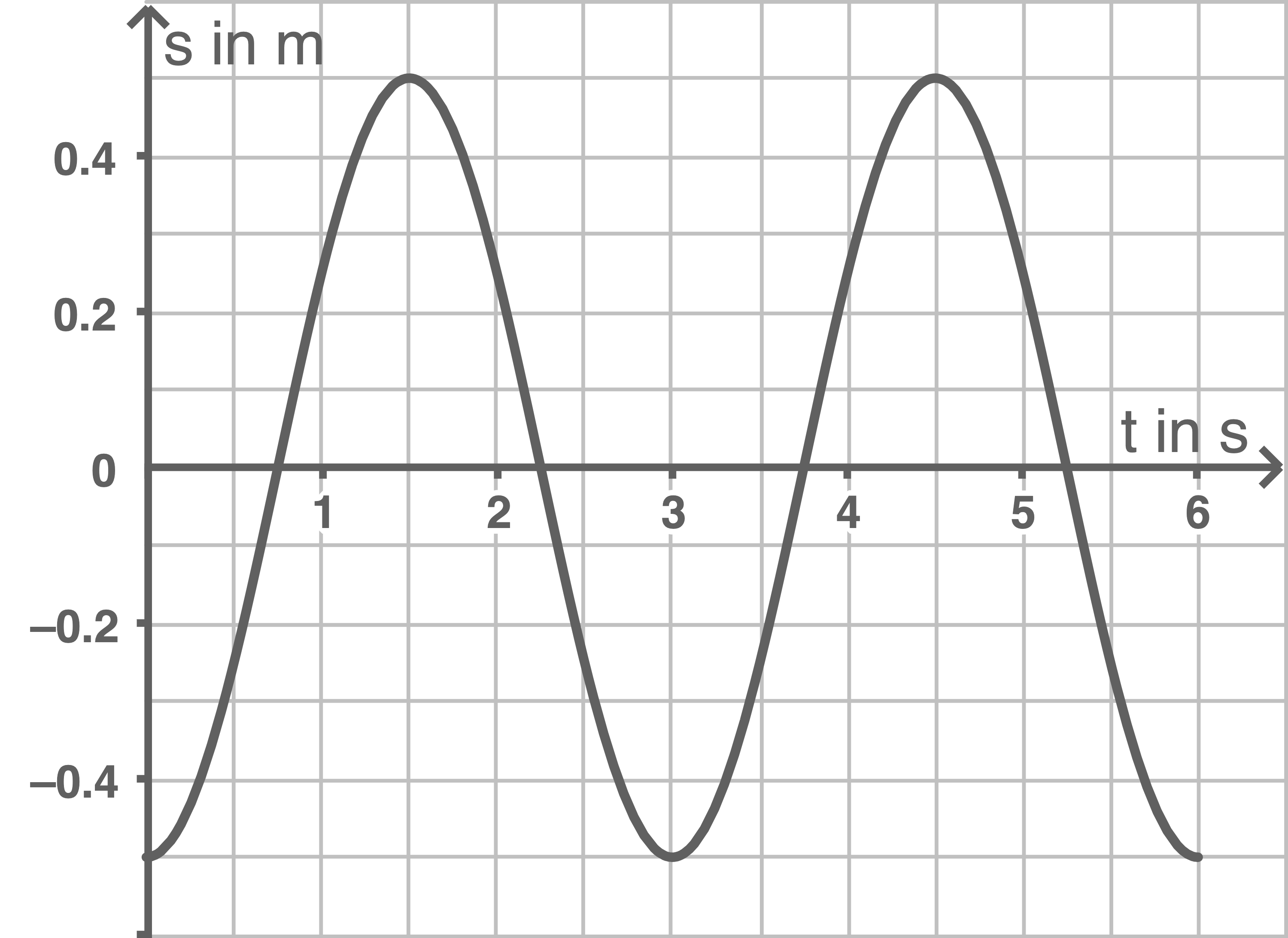

Abbildung 1 a

Abbildung 1 b
a)
Gib die Periodendauer an.
b)
Bestimme den Betrag der maximalen Geschwindigkeit.
c)
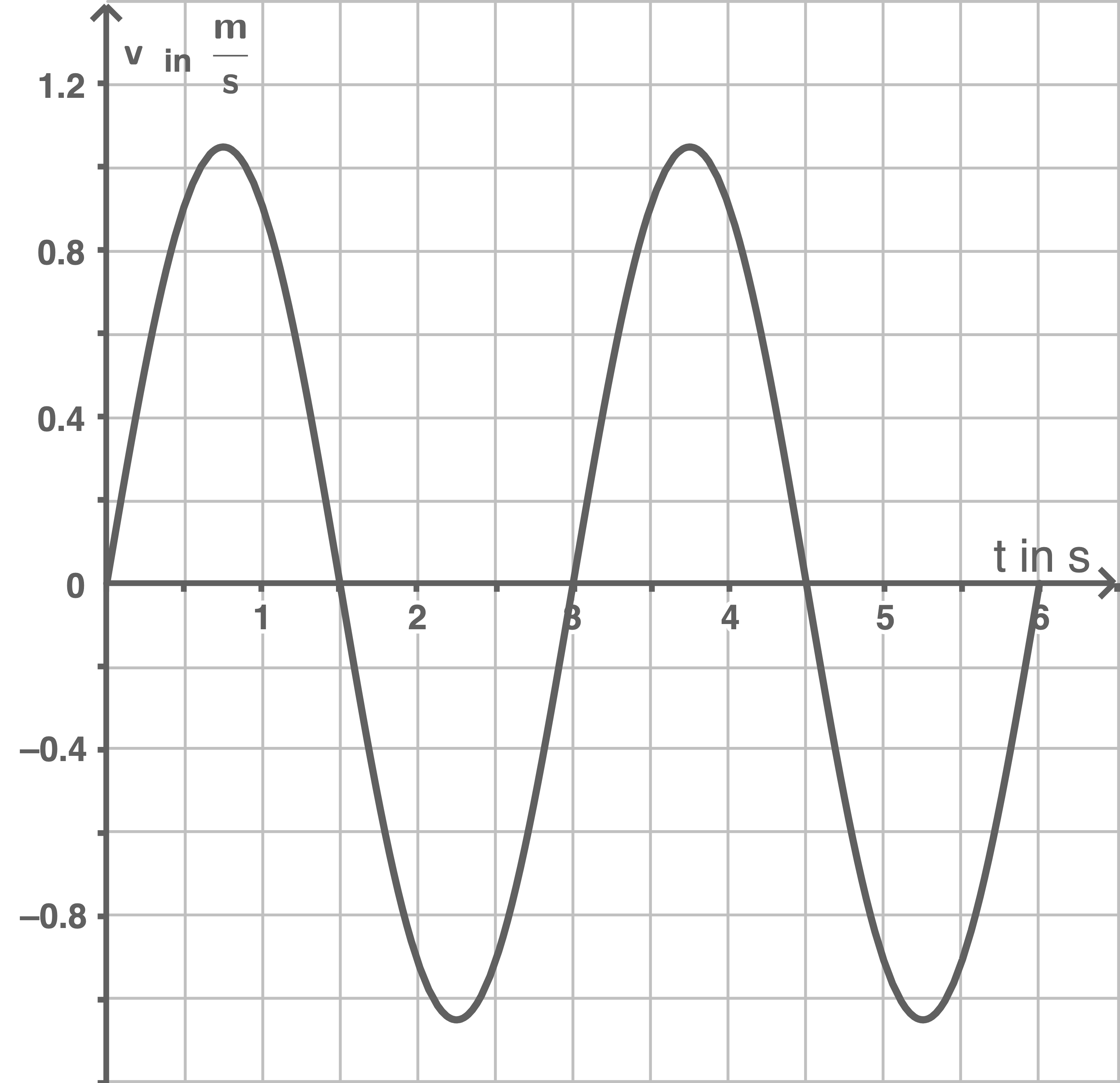
Skizziere das zugehörige Zeit-Geschwindigkeit-Diagramm für die ersten 
Das Kind wird während der Bewegung angestoßen. Dadurch liegt der Umkehrpunkt gegenüber der Ruhelage im Vergleich zu vorher um 30 % höher.
d)
Berechne die Änderung der maximalen Geschwindigkeit.
(7 VP)
2.
In einem mit Wasser gefüllten Becken befindet sich an den Punkten  und
und  jeweils ein Stift, der von oben senkrecht in die Wasseroberfläche eintaucht. Die beiden Stifte beginnen zum Zeitpunkt
jeweils ein Stift, der von oben senkrecht in die Wasseroberfläche eintaucht. Die beiden Stifte beginnen zum Zeitpunkt  harmonisch und gleichphasig mit der Frequenz
harmonisch und gleichphasig mit der Frequenz  nach unten zu schwingen, die Ausbreitungsgeschwindigkeit der dabei erzeugten Wellen auf der Wasseroberfläche beträgt
nach unten zu schwingen, die Ausbreitungsgeschwindigkeit der dabei erzeugten Wellen auf der Wasseroberfläche beträgt  , die Amplitude der Wellen
, die Amplitude der Wellen  Von Reflexion und Dämpfung wird abgesehen.
Von Reflexion und Dämpfung wird abgesehen.
Ab einem bestimmten Zeitpunkt überlagern sich die von den Punkten und
und  ausgehenden Wellen im Punkt
ausgehenden Wellen im Punkt  (siehe Abbildung 2).
(siehe Abbildung 2).
Ab einem bestimmten Zeitpunkt überlagern sich die von den Punkten
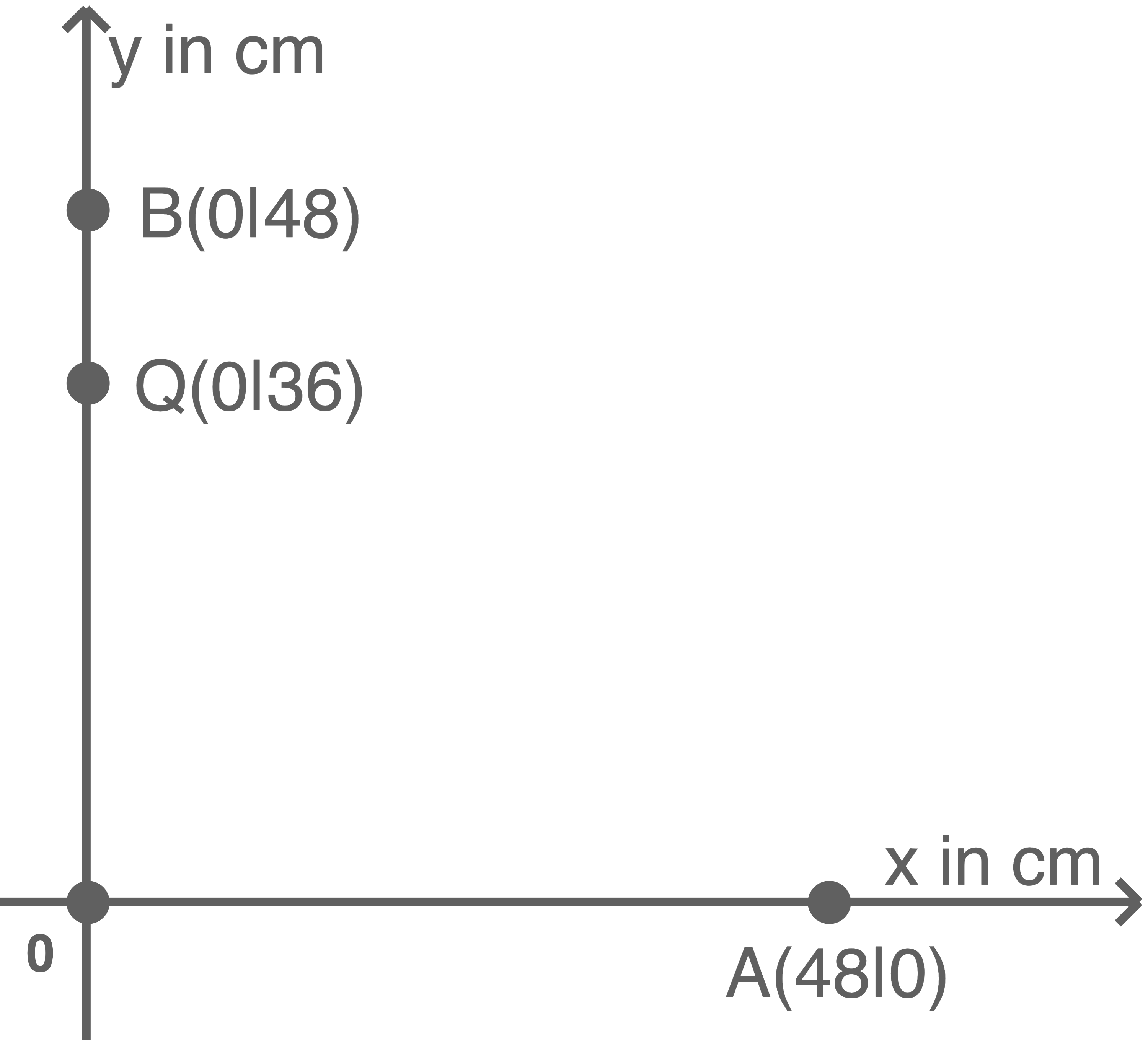
Abbildung 2
a)
Bestimme den Gangunterschied der beiden Wellen im Punkt 
b)
Zeichne für das Zeitintervall von  ein Zeit-Auslenkung-Diagramm für den Punkt
ein Zeit-Auslenkung-Diagramm für den Punkt  und dokumentiere dein Vorgehen.
und dokumentiere dein Vorgehen.
Abbildung 3 zeigt, wie die Ausbreitungsgeschwindigkeit 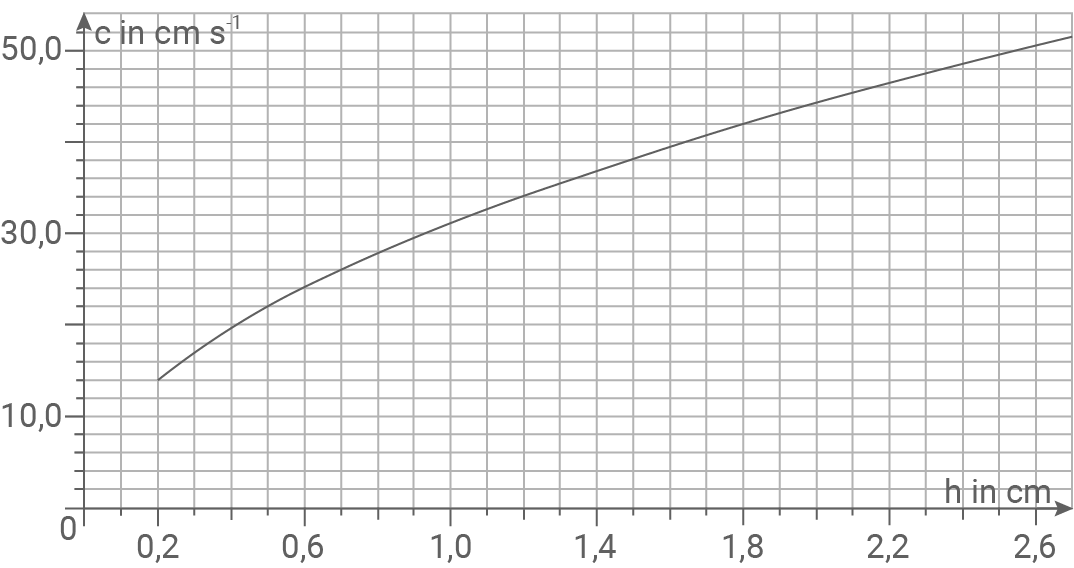
Abbildung 3
c)
Bestimme eine Wassertiefe, für welche im Punkt  konstruktive Interferenz beobachtbar ist.
konstruktive Interferenz beobachtbar ist.
(8 VP)
3.
Ein  langer beidseitig eingespannter Eisendraht wird an einer geeigneten Stelle durch einen Elektromagneten zu harmonischen Schwingungen angeregt, die Erregerfrequenz wird dabei von
langer beidseitig eingespannter Eisendraht wird an einer geeigneten Stelle durch einen Elektromagneten zu harmonischen Schwingungen angeregt, die Erregerfrequenz wird dabei von  aus langsam erhöht. Bei
aus langsam erhöht. Bei  beobachtet man erstmals, dass die Mitte des Drahts dauerhaft in Ruhe bleibt.
beobachtet man erstmals, dass die Mitte des Drahts dauerhaft in Ruhe bleibt.
 dann in einem weiteren Experiment mit
dann in einem weiteren Experiment mit  angeregt.
angeregt.
Sofja: „Der muss nicht ruhen. An der Stelle ist dann ein Knoten.“
Anna: „Das ist möglich, wenn es sich um eine Eigenschwingung handelt.“
Ilona: „Das kann keine Eigenschwingung sein. Das würde der Energieerhaltung widersprechen.“
a)
Bestimme die Ausbreitungsgeschwindigkeit der vom Erreger erzeugten Welle im Eisendraht.
Der Draht wird nun zunächst mit der Frequenz 
b)
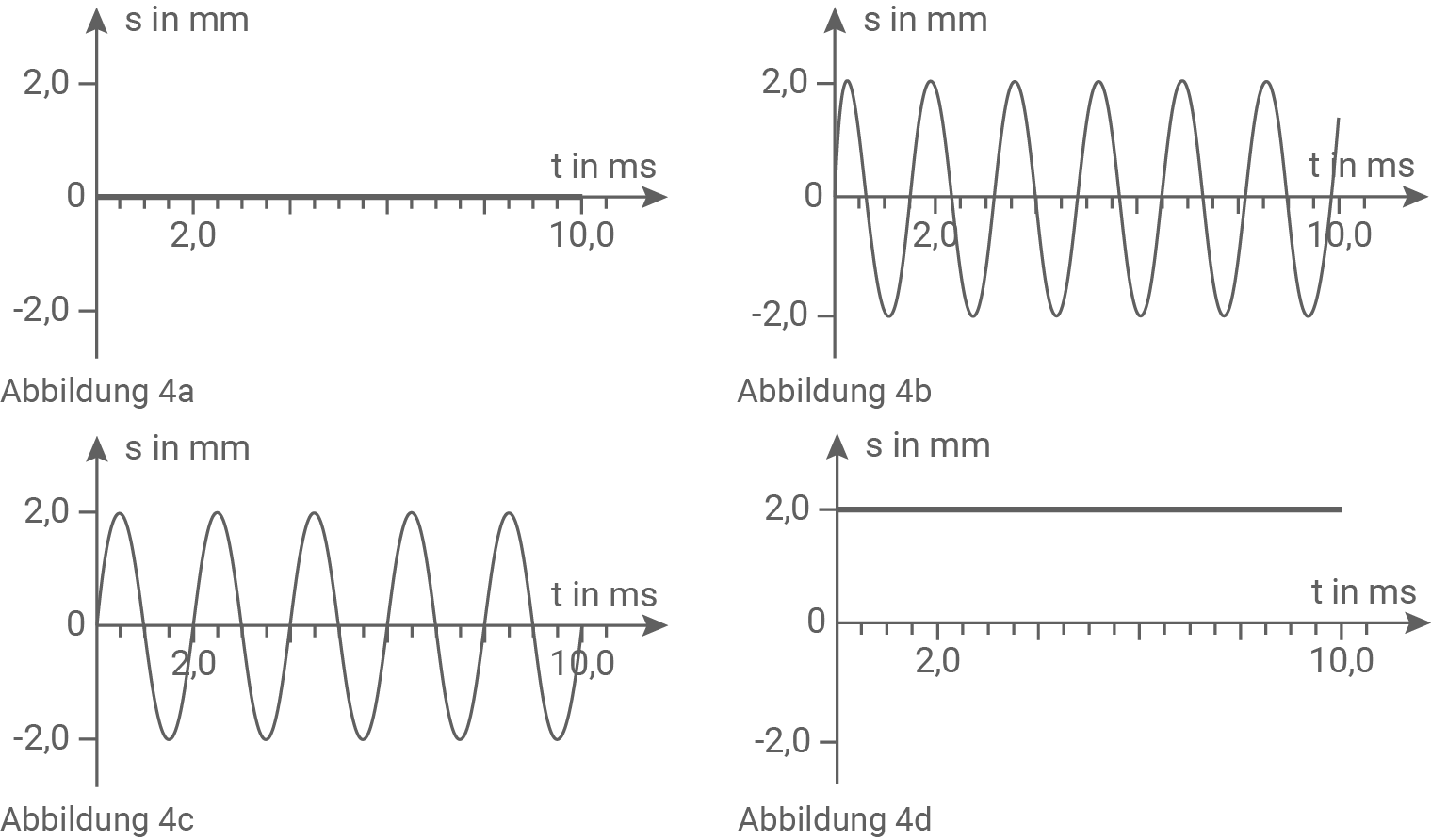
Überprüfe, ob es nach dem Einschwingvorgang zwischen den beiden eingespannten Enden Punkte auf dem Draht gibt, für die die voranstehenden Zeit-Auslenkung-Diagramme prinzipiell möglich sind (siehe Abbildung 4a bis 4d).
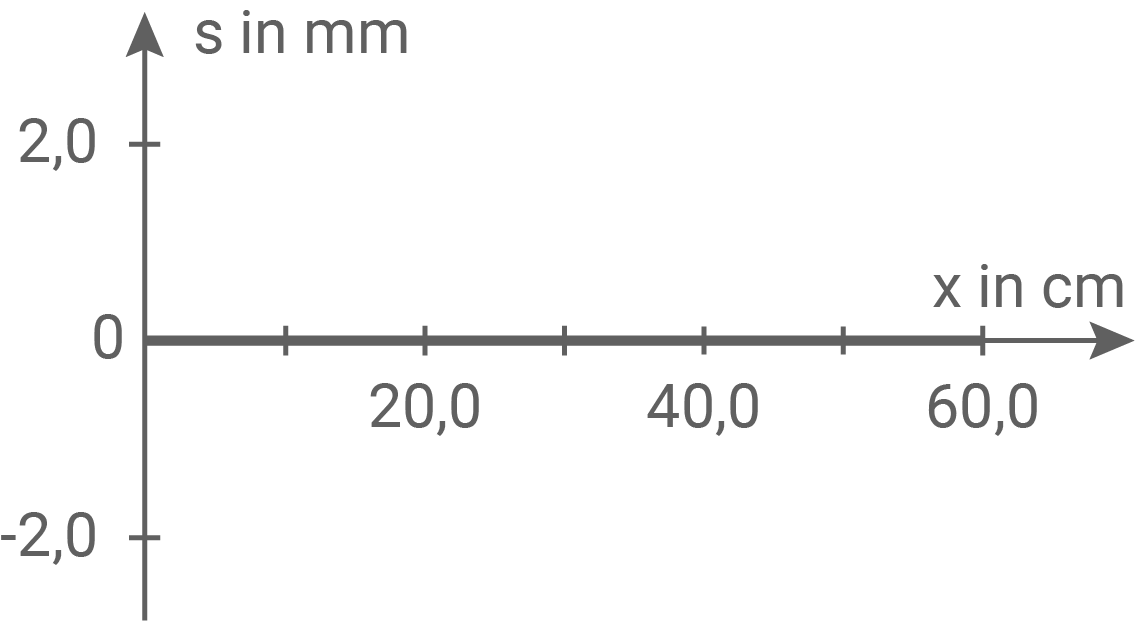
Eine Schülergruppe diskutiert, ob das Diagramm in Abbildung 5 ein Momentanbild des Drahts sein könnte.
Julia: „Das kann nur sein, wenn der Draht ruht.“
Sofja: „Der muss nicht ruhen. An der Stelle ist dann ein Knoten.“
Anna: „Das ist möglich, wenn es sich um eine Eigenschwingung handelt.“
Ilona: „Das kann keine Eigenschwingung sein. Das würde der Energieerhaltung widersprechen.“

Abbildung 5
c)
Beurteile jede der vier Aussagen.
(9 VP)
4.
In einer geeigneten Anordnung werden einzelne Elektronen mithilfe einer Gleichspannung von  aus der Ruhe heraus beschleunigt. Sie treffen senkrecht auf einen Doppelspalt mit
aus der Ruhe heraus beschleunigt. Sie treffen senkrecht auf einen Doppelspalt mit  Spaltmittenabstand. Im Abstand von
Spaltmittenabstand. Im Abstand von  hinter der Spaltebene befindet sich ein Detektor, mit dessen Hilfe die Positionen der auftreffenden Elektronen dauerhaft registriert werden können.
hinter der Spaltebene befindet sich ein Detektor, mit dessen Hilfe die Positionen der auftreffenden Elektronen dauerhaft registriert werden können.
a)
Erläutere, wie sich die Verteilung der Nachweispunkte im Laufe der Zeit entwickelt hat.
b)
Berechne den Abstand benachbarter Maxima.
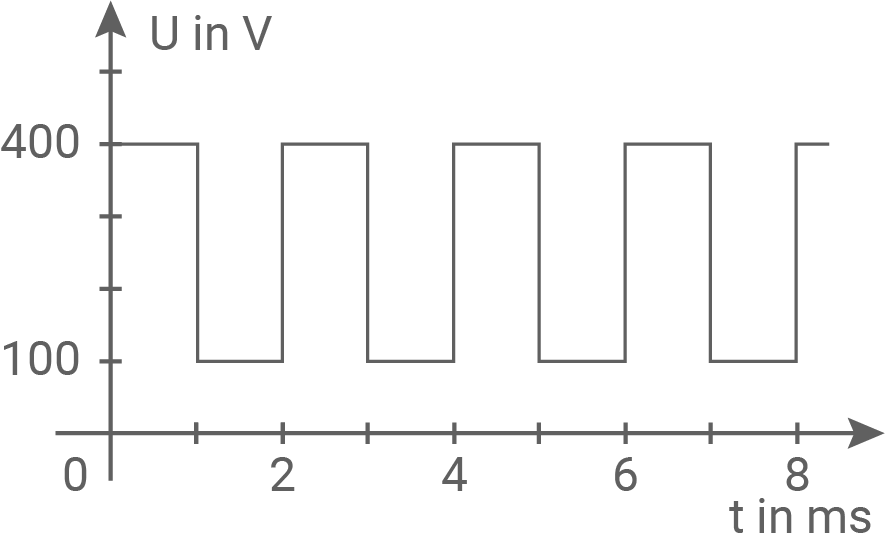
Es wird nun vorgeschlagen, das Experiment zu wiederholen und dabei anstelle der Gleichspannung eine Beschleunigungsspannung zu verwenden, deren zeitlicher Verlauf in Abbildung 6 dargestellt ist.

Abbildung 6
c)
Gib eine Hypothese dazu an, wie sich die beiden Verteilungen der Nachweispunkte der Elektronen in den Experimenten unterscheiden könnten und begründe deine Hypothese.
(6 VP)
1
a)
Die Periodendauer wird aus dem Diagramm abgelesen: Sie ist der zeitliche Abstand zwischen zwei Maxima. Dieser beträgt  . Somit ist die Periodendauer
. Somit ist die Periodendauer 
b)
Für die maximale Geschwindigkeit bei einem Pendel gilt:  Die maximale Auslenkung
Die maximale Auslenkung  wird mit
wird mit  aus dem Diagramm abgelesen.
aus dem Diagramm abgelesen.
![\(\begin{array}[t]{rll}
\hat{v} &=& \hat{s} \cdot \omega &\quad \scriptsize \mid\; \omega = \frac{2 \pi}{T} \\[5pt]
\hat{v} &=& \dfrac{\hat{s} \cdot 2 \pi}{T} \\[5pt]
\hat{v} &=& \dfrac{0,5 \text{ cm} \cdot 2 \pi}{3,0 \text{ s}} \\[5pt]
\hat{v} &=& 1,05 \;\frac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/166b6d45d97d5e9cfb24ed87662eca3f1ad3771e1dd21267fa69ac1b2e26917f_light.svg)
c)
Das gegebene Zeit-Auslenkung-Diagramm wird durch folgende Funktion beschrieben:  Da die Geschwindigkeit die zeitliche Ableitung der Auslenkung ist, ergibt sich für die Geschwindigkeitsfunktion:
Da die Geschwindigkeit die zeitliche Ableitung der Auslenkung ist, ergibt sich für die Geschwindigkeitsfunktion:
![\(\begin{array}[t]{rll}
v(t) &=& \dot{s}(t) \\[5pt]
v(t) &=& \hat{s} \cdot \omega \cdot \sin (\omega \cdot t) &\quad \scriptsize \mid\; \hat{v} = \hat{s} \cdot \omega \\[5pt]
v(t) &=& \hat{v} \cdot \sin (\omega \cdot t) \\[5pt]
v(t) &=& 1,05 \text{ } \dfrac{\text{m}}{\text{s}} \cdot \sin (\omega \cdot t)
\end{array}\)](https://www.schullv.de/resources/formulas/0d1d55042391905c3d91949b3616d3a92a9155b96ad13ab003d732167aa2b77b_light.svg)

d)
Achtung: Es wird angegeben, wie sich der Umkehrpunkt ändert. Aber es wird nicht angegeben, wie sich die maximale Auslenkung verändert. Es darf also nicht ohne weiteres mit der Auslenkungsformel gerechnet werden. Die Aufgabe wird am besten wie folgt über den Energieerhaltungssatz gelöst:
Wenn der Umkehrpunkt um  nach oben versetzt wird, dann nimmt auch die Lageenergie um
nach oben versetzt wird, dann nimmt auch die Lageenergie um  zu, da
zu, da  gilt. Folglich nimmt auch die kinetische Energie um
gilt. Folglich nimmt auch die kinetische Energie um  zu.
zu.
![\(\begin{array}[t]{rll}
\hat{W}_{\text{kin}_{\text{neu}}}&=& 1,3 \cdot \hat{W}_{\text{kin}_{\text{neu}}} \\[5pt]
\dfrac{1}{2} \cdot m \cdot {v}_{\text {neu }}^{2} &=& 1,3 \cdot \dfrac{1}{2} \cdot m \cdot {v}_{\text {alt }}^{2} &\quad \scriptsize \mid\; :\frac{m}{2} \\[5pt]
{v}_{\text {neu }}^{2} &=& 1,3 \cdot {v}_{\text {alt }}^{2} &\quad \scriptsize \mid\; \sqrt{(...)} \\[5pt]
{v}_{\text {neu }} &=& \sqrt{1,3} \cdot {v}_{\text {alt }} \\[5pt]
{v}_{\text {neu }} &=& 1,14 \cdot {v}_{\text {alt }} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/92b124f5a5751ef2d7bffa1b59c36d322cc1540ded91eb81560e42169b69adec_light.svg) Die maximale Geschwindigkeit hat sich folglich um
Die maximale Geschwindigkeit hat sich folglich um  erhöht. Die absolute Änderung beträgt somit:
erhöht. Die absolute Änderung beträgt somit:


2
a)
Gegeben: 


 Gesucht:
Gesucht:  Lösung:
1. Schritt: Berechnung der Entferung beider Stifte zu Punkt
Lösung:
1. Schritt: Berechnung der Entferung beider Stifte zu Punkt 

 Der Abstand zwischen dem Punkt
Der Abstand zwischen dem Punkt  und
und  ergibt sich aus dem Satz des Pythagoras:
2. Schritt: Berechnung der Wellenlänge
ergibt sich aus dem Satz des Pythagoras:
2. Schritt: Berechnung der Wellenlänge
![\(\begin{array}[t]{rll}
\lambda \cdot f &=& c &\quad \scriptsize \mid\; : f \\[5pt]
\lambda &=& \dfrac{c}{f} \\[5pt]
\lambda &=& \dfrac{32 \text{ } \frac{\text{cm}}{\text{s}}}{1,0 \text{ } \frac{1}{\text{s}} } \\[5pt]
\lambda &=& 32 \text{ cm}
\end{array}\)](https://www.schullv.de/resources/formulas/e828430509922b42cb5105a1a1c804096e33f599d26082454dca2659f0040ff8_light.svg) 3. Schritt: Berechnung des Gangunterschieds
3. Schritt: Berechnung des Gangunterschieds


![\(\begin{array}[t]{rll}
\delta &=& \dfrac{\Delta s}{\lambda} \\[5pt]
\delta &=& \dfrac{48 \;\text{cm}}{32 \text{ cm}} \\[5pt]
\delta &=& 1,5
\end{array}\)](https://www.schullv.de/resources/formulas/553b97f9ae92455e258681525cf53f9396d26d302393006b473cd7aa44face10_light.svg) Der Gangunterschied im Punkt
Der Gangunterschied im Punkt  beträgt
beträgt  Wellenlängen.
Wellenlängen.
b)
1. Schritt: Vorüberlegung
Zu Beginn bleibt der Punkt  in Ruhe. Dann trifft in
in Ruhe. Dann trifft in  die erste Wellenfront von dem Stift
die erste Wellenfront von dem Stift  ein, da dieser näher an
ein, da dieser näher an  liegt als der Stift
liegt als der Stift  Da die beiden Stifte nach Aufgabenstellung nach unten anfangen zu schwingen, trifft zuerst ein Wellental ein. Mit einem gewissen zeitlichen Abstand trifft die Wellenfront von dem Stift
Da die beiden Stifte nach Aufgabenstellung nach unten anfangen zu schwingen, trifft zuerst ein Wellental ein. Mit einem gewissen zeitlichen Abstand trifft die Wellenfront von dem Stift  ein. Da der Gangunterschied der beiden Stifte in Punkt
ein. Da der Gangunterschied der beiden Stifte in Punkt 
 beträgt, tritt destruktive Interferenz auf und die beiden Wellen löschen sich in
beträgt, tritt destruktive Interferenz auf und die beiden Wellen löschen sich in  aus. Somit hört
aus. Somit hört  auf zu schwingen.
2. Schritt: Berechnung des Zeitpunkts an dem die Wellen von Stift B ankommen
auf zu schwingen.
2. Schritt: Berechnung des Zeitpunkts an dem die Wellen von Stift B ankommen
 3. Schritt: Berechnung des Zeitpunkts an dem die Wellen von Stift A ankommen
3. Schritt: Berechnung des Zeitpunkts an dem die Wellen von Stift A ankommen
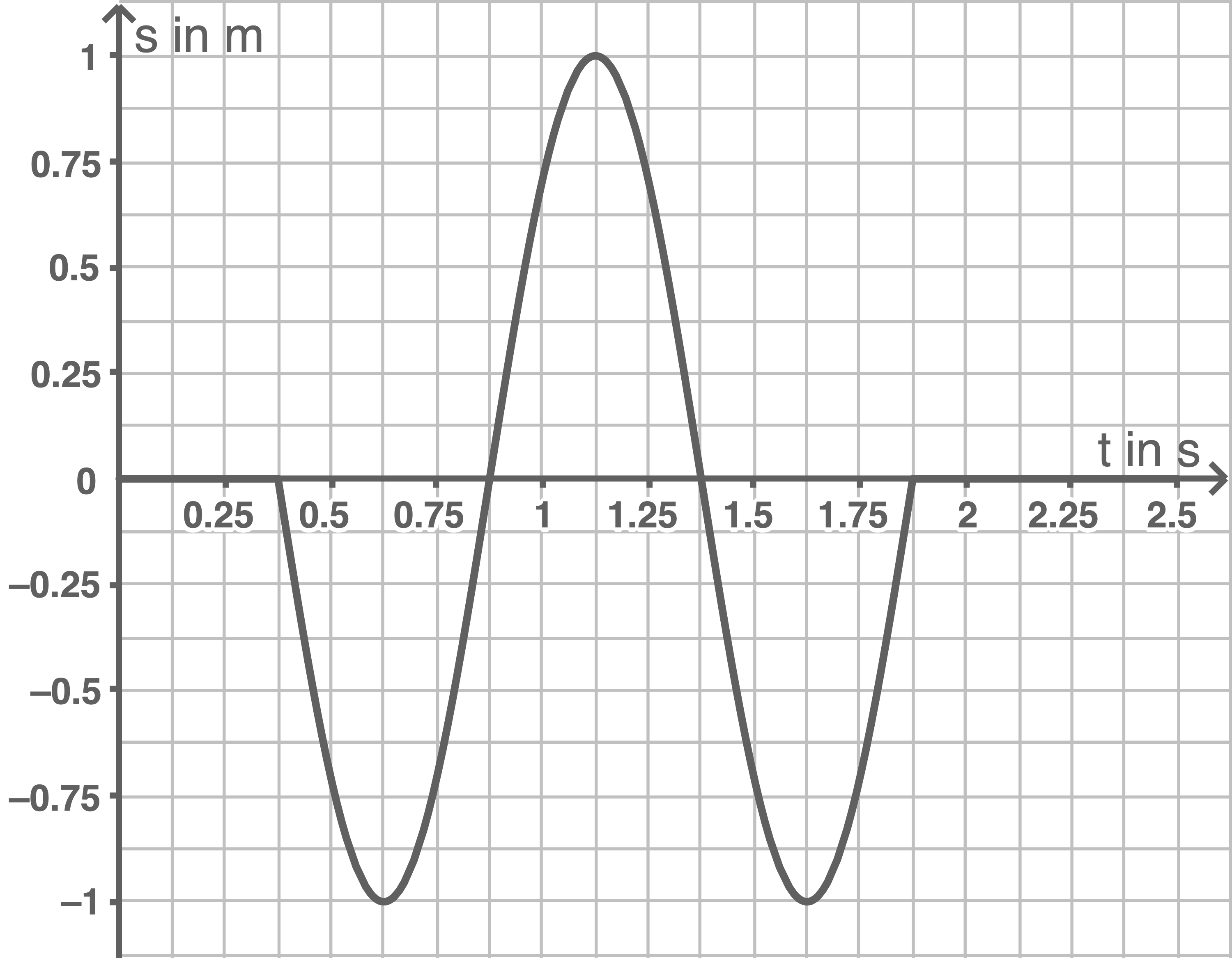
 4. Schritt: Diagramm zeichen
Hinweis: Da der Gangunterschied der beiden Stifte
4. Schritt: Diagramm zeichen
Hinweis: Da der Gangunterschied der beiden Stifte  Wellenlängen beträgt, schwingt der Punkt
Wellenlängen beträgt, schwingt der Punkt  vom Zeitpunkt
vom Zeitpunkt  bis zum Zeitpunkt
bis zum Zeitpunkt  eineinhalb mal. Die Amplitude beträgt laut Aufgabenstellung
eineinhalb mal. Die Amplitude beträgt laut Aufgabenstellung 

c)
Um konstruktive Interferenz zu erreichen, muss der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge  sein. Da die Frequenz
sein. Da die Frequenz  nach Aufgabenstellung
nach Aufgabenstellung  beträgt, gilt:
beträgt, gilt: 
 Somit kann eine Ausbreitungsgeschwindigkeit
Somit kann eine Ausbreitungsgeschwindigkeit  von
von  gewählt werden, um einen Gangunterschied von
gewählt werden, um einen Gangunterschied von  zu erzeugen. Um eine Ausbreitungsgeschwindigkeit
zu erzeugen. Um eine Ausbreitungsgeschwindigkeit  von
von  zu erreichen, muss die Wassertiefe
zu erreichen, muss die Wassertiefe  aufgrund des im Diagramm dargestellten Zusammenhangs
aufgrund des im Diagramm dargestellten Zusammenhangs  betragen.
betragen.
3
a)
Da der Draht beidseitig eingespannt ist, wird es bei gewissen Frequenzen zur Eigenschwingung kommen.
Für die Grundschwingung gilt: Somit schwingt der Draht mit einem Bauch in der Mitte. Wird die Frequenz verdoppelt, so wird diese die 1. Oberfrequenz genannt und es kommt ein Bauch hinzu. Es gilt:
Somit schwingt der Draht mit einem Bauch in der Mitte. Wird die Frequenz verdoppelt, so wird diese die 1. Oberfrequenz genannt und es kommt ein Bauch hinzu. Es gilt:  Folglich bleibt nun die Mitte des Drahts das erst mal in Ruhe.
Somit ergibt sich für die Ausbreitungsgeschwindigkeit:
Folglich bleibt nun die Mitte des Drahts das erst mal in Ruhe.
Somit ergibt sich für die Ausbreitungsgeschwindigkeit:
![\(\begin{array}[t]{rll}
c&=& \lambda \cdot f &\quad \scriptsize \mid\; \lambda = \ell \\[5pt]
c&=& \ell \cdot f \\[5pt]
c&=& 0,600 \text{ m} \cdot 400 \text{ Hz} \\[5pt]
c&=& 240 \text{ } \dfrac{\text{m}}{\text{s}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8d1d02546e3b2386608e6d6975c8218e8f376ce413e1410f954270c8c9175cd2_light.svg)
Für die Grundschwingung gilt:
b)
Vorüberlegung
Bei einer Frequenz von  treten keine Eigenschwingungen auf, da die
treten keine Eigenschwingungen auf, da die  kein Vielfaches der Grundfrequenz von
kein Vielfaches der Grundfrequenz von  sind. Somit gibt es keinen Stelle auf dem Draht die in Ruhe bleibt oder sinusförmig schwingt.
Bei einer Frequenz von
sind. Somit gibt es keinen Stelle auf dem Draht die in Ruhe bleibt oder sinusförmig schwingt.
Bei einer Frequenz von  kommt es zur 2. Oberschwingung, da die
kommt es zur 2. Oberschwingung, da die  das Dreifache der Grundfrequenz von
das Dreifache der Grundfrequenz von  sind. Es gibt somit drei Schwingungsbäume und zwei Schwingungsknoten.
Abb. 4a
Mit einer Frequenz von
sind. Es gibt somit drei Schwingungsbäume und zwei Schwingungsknoten.
Abb. 4a
Mit einer Frequenz von  beschreibt dieses Diagramm die Stelle
beschreibt dieses Diagramm die Stelle  (erster Knoten) und die Stelle
(erster Knoten) und die Stelle  (zweiter Knoten).
Abb. 4b
Im Zeitraum von
(zweiter Knoten).
Abb. 4b
Im Zeitraum von  bis
bis  finden
finden  Schwingungen statt. Somit ergibt sich eine Periodendauer von
Schwingungen statt. Somit ergibt sich eine Periodendauer von  Diese gehört zu folgender Frequenz:
Diese gehört zu folgender Frequenz:


 Folglich kann das Diagramm die Auslenkung an einer Stelle auf dem Draht für eine Frequenz von
Folglich kann das Diagramm die Auslenkung an einer Stelle auf dem Draht für eine Frequenz von  beschreiben.
Abb. 4c
Die Periodendauer beträgt
beschreiben.
Abb. 4c
Die Periodendauer beträgt  . Somit beträgt die Frequenz
. Somit beträgt die Frequenz  . Da bei einer Frequenz von
. Da bei einer Frequenz von  keine Eigenfrequenz auftritt, ist dieses Diagramm nicht möglich.
Abb. 4d
Bei der in der Aufgabenbestellung beschriebenen Schwingung existiert kein Punkt, der konstant ausgelenkt ist. Somit ist dieses Diagramm nicht möglich.
keine Eigenfrequenz auftritt, ist dieses Diagramm nicht möglich.
Abb. 4d
Bei der in der Aufgabenbestellung beschriebenen Schwingung existiert kein Punkt, der konstant ausgelenkt ist. Somit ist dieses Diagramm nicht möglich.
c)
Julia's Aussage
Julia's Aussage ist falsch. Falls es sich bei der Schwingung um eine Eigenschwingung handelt, gibt es Zeitpunkte an dem der komplette Draht nicht ausgelekt ist.
Sofja's Aussage
Sofja's Aussage ist falsch. Sie bezieht sich auf ein Zeit-Auslenkugsdiagramm und meint einen Punkt. Das gegebene Diagramm beschreibt aber die Auslenkung des gesammten Drahts zu einem gewissen Zeitpunkt.
Anna's Aussage
Anna's Aussage ist richtig. Bei einer Eigenschwingung gibt es Zeitpunkte, an denen der komplette Draht nicht ausgelenkt ist.
Lara's Aussage
Lara's Aussage ist falsch. Wenn bei der Eigenschwingung der Draht nicht ausgelenkt ist, dann ist die kinetischer Energie zu diesem Zeitpunkt maximal. Der Energieerhaltungssatz wird somit nicht verletzt.
4
a)
Elektronen können analog zu Photonen Welleneigenschaften zugewiesen werden. Hierbei beschreibt die De-Brogie-Wellenlänge diese. Wenn die Elektronen auf ein ausreichend feinen Doppelspalt treffen, so tritt aufgrund der quantenmechanischen Eigenschaften Beugung und folglich auch Interferenz auf. Das Muster welches sich auf dem Schirm bildet, wirkt zunächst zufällig. Mit fortschreitender Zeit bildet sich jedoch einige Minima und Maxima. Das resultierende Interferenzmuster gleicht dem eines Doppelspalts, der mit monochromatischem Licht bestrahlt wird.
b)
1. Schritt: Geschwindigkeit des Elektrons
Die Energie, die das Elektron im E-Feld aufnimmt ist gegeben durch folgende Formel:  Somit kann mit der Formel der kinetsichen Energie die Geschwindigkeit des Elektrons ermittelt werden:
Somit kann mit der Formel der kinetsichen Energie die Geschwindigkeit des Elektrons ermittelt werden:
![\(\begin{array}[t]{rll}
E_{\text{el}}&=& E_{\text{kin}} \\[5pt]
e \cdot U &=& \dfrac{1}{2} \cdot m \cdot v^2 &\quad \scriptsize \mid\; \cdot \dfrac{2}{m} \\[5pt]
\dfrac{2 \cdot e \cdot U}{m} &=& v^2 &\quad \scriptsize \mid\; \sqrt{(\;)} \\[5pt]
\sqrt{\dfrac{2 \cdot e \cdot U}{m}} &=& v \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/daf4f21cf8f30c1e639875dbe740370d1c971e32b8befd2ca519bd1b8a20b32b_light.svg) 2. Schritt: Impuls des Elektrons
Die Formel für den Impuls lautet:
2. Schritt: Impuls des Elektrons
Die Formel für den Impuls lautet:
![\(\begin{array}[t]{rll}
p &=& m \cdot v \\[5pt]
p &=& m \cdot \sqrt{\dfrac{2 \cdot e \cdot U}{m}} \\[5pt]
p &=& \sqrt{2 \cdot e \cdot U}
\end{array}\)](https://www.schullv.de/resources/formulas/83684b390abb1adbdd47316fa8d4d35d1a505f7d7a55569ce0e5a03a0c292d96_light.svg) 3. Schritt: De-Brogie-Wellenlänge
Die Formel für die De-Brogie-Wellenlänge lautet:
3. Schritt: De-Brogie-Wellenlänge
Die Formel für die De-Brogie-Wellenlänge lautet:
![\(\begin{array}[t]{rll}
\lambda &=& \dfrac{h}{p} \\[5pt]
\lambda &=& \dfrac{h}{\sqrt{2 \cdot e \cdot U}} \\[5pt]
\lambda &=& \dfrac{6,63 \cdot 10^{-34}}{\sqrt{2 \cdot 1,60 \cdot 10^{-19} \cdot 400}} \text{ m} \\[5pt]
\lambda &=& 6,14 \cdot 10^{-11} \text{ m}
\end{array}\)](https://www.schullv.de/resources/formulas/88a2fc97f9f67919373bfc234915ece7701af98e0e163639d2931c9d4790b84e_light.svg) 4. Schritt: Beugungsformeln
Es gelten die beiden Beugungsformeln:
4. Schritt: Beugungsformeln
Es gelten die beiden Beugungsformeln:  und
und 
Da die Winekl bei der Elektronenbeugung sehr klein sind kann die Kleinwinkelnäherung angewandt werden: Solange die Kleinwinkelnäherung anwendbar ist, ist der Abstand zwischen zwei Maxima konstant und beträgt ca.
Da die Winekl bei der Elektronenbeugung sehr klein sind kann die Kleinwinkelnäherung angewandt werden: Solange die Kleinwinkelnäherung anwendbar ist, ist der Abstand zwischen zwei Maxima konstant und beträgt ca.
c)
Hypothese: Bei der neuen Verteilungen der Nachweispunkte der Elektronen wird jedes geradzahlige Maximum der Elektronen, die mit  beschleunigt werden von einem Maximum der Elektronen, die mit
beschleunigt werden von einem Maximum der Elektronen, die mit  bescheunigt werden, überlagert. Diese Hypothese ergibt sich aus folgendem Zusammenhang aus der Teilaufgabe b):
bescheunigt werden, überlagert. Diese Hypothese ergibt sich aus folgendem Zusammenhang aus der Teilaufgabe b):
 somit ist
somit ist  Also halbiert sich die Wellenlänge bei einer Vervierfachung der Spannung. Nach Teilaufgabe b) gilt:
Also halbiert sich die Wellenlänge bei einer Vervierfachung der Spannung. Nach Teilaufgabe b) gilt:
 somit ist ungefähr
somit ist ungefähr  Folglich halbiert sich auch grob der Abstand der Maxima bei einer Vervierfachung der Spannung.
Folglich halbiert sich auch grob der Abstand der Maxima bei einer Vervierfachung der Spannung.