Aufgabe 4 – Elektromagnetismus
1.
In einem ungedämpften elektromagnetischen Schwingkreis wird mit einem Messwerterfassungssystem die Stromstärke als Funktion der Zeit aufgenommen. Die Induktivität der Spule beträgt  . Abbildung 1 zeigt den zeitlichen, sinusförmigen Verlauf der Stromstärke im Schwingkreis.
. Abbildung 1 zeigt den zeitlichen, sinusförmigen Verlauf der Stromstärke im Schwingkreis.
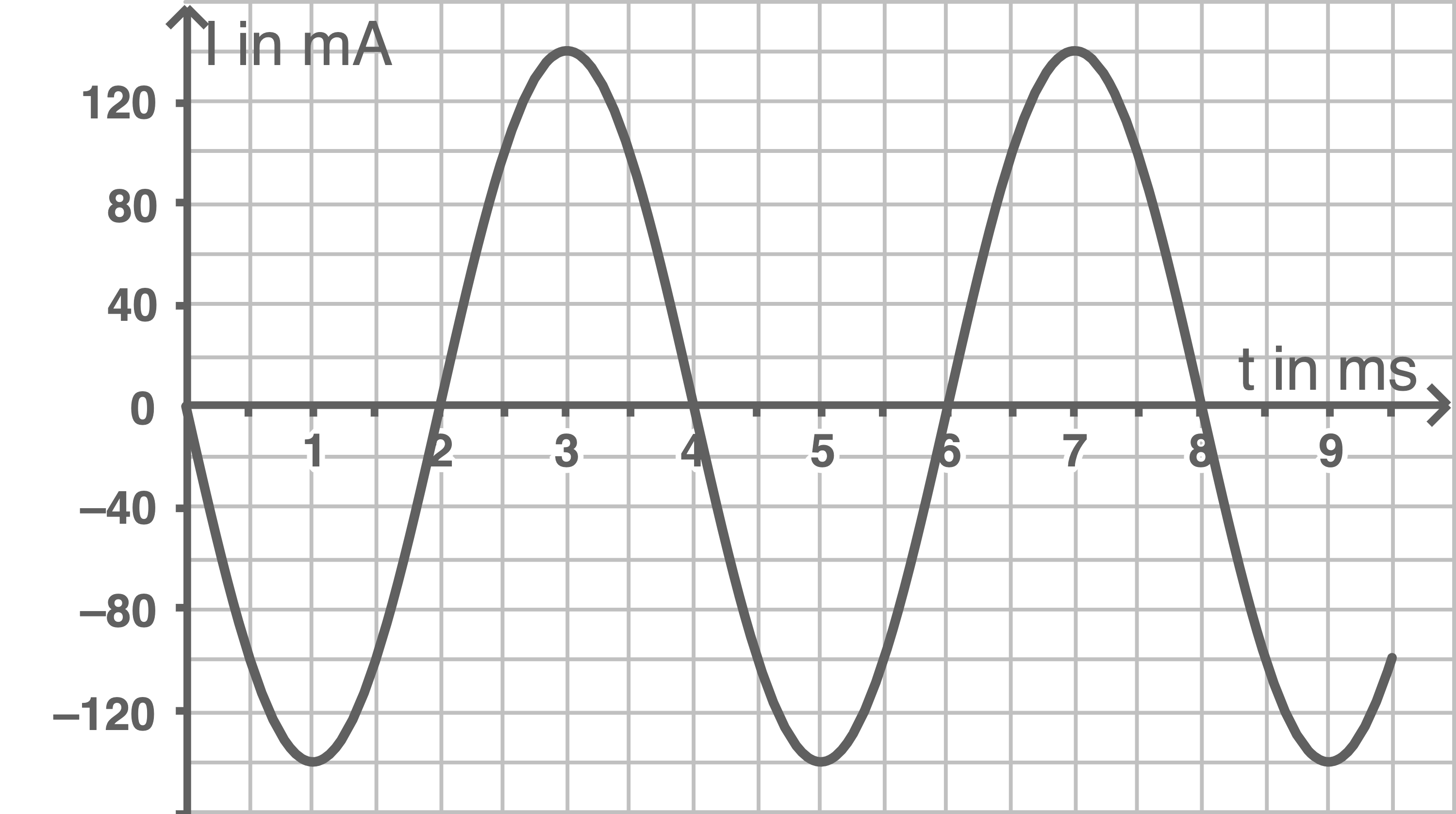

Abbildung 1
a)
Bestimme die Frequenz des Schwingkreises.
b)
Ermittle die Kapazität des Kondensators.
c)
Bestimme die Werte, zwischen denen die Energie des Magnetfeldes schwankt.
d)
Bestimme mit Hilfe des Diagramms den ersten Zeitpunkt, bei dem sich die halbe maximale Energie im Magnetfeld der Spule befindet.
e)
Zeichne ein geeignetes Zeit - Spannung - Diagramm für die Spannung  am Kondensator.
am Kondensator.
(9 VP)
2.
Zwei quadratische Leiterrahmen (1) und (2) befinden sich oberhalb eines scharf begrenzten homogenen Magnetfelds. Die magnetische Flussdichte beträgt  und die Feldlinien weisen senkrecht in die Zeichenebene. Beide Rahmen haben eine Kantenlänge von
und die Feldlinien weisen senkrecht in die Zeichenebene. Beide Rahmen haben eine Kantenlänge von  und jeweils eine Masse von
und jeweils eine Masse von  (siehe Abb. 2). Vom Luftwiderstand wird abgesehen.
(siehe Abb. 2). Vom Luftwiderstand wird abgesehen.
Zunächst lässt man Rahmen (1) aus der in Abbildung 2 gezeichneten Position fallen.
Zunächst lässt man Rahmen (1) aus der in Abbildung 2 gezeichneten Position fallen.
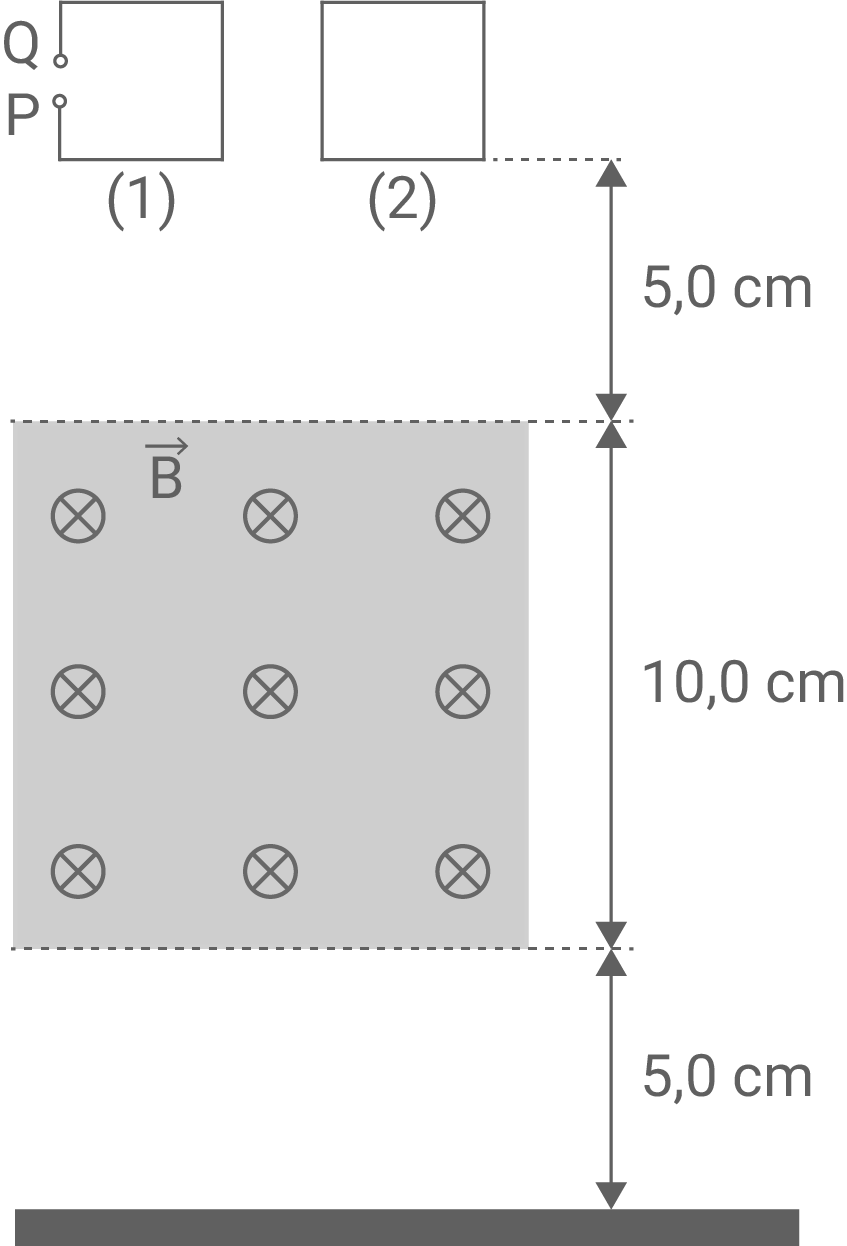
Abbildung 2
a)
Erkläre, dass beim Eintritt in das Magnetfeld zwischen den Leiterenden  und
und  eine Spannung auftritt.
eine Spannung auftritt.
b)
Gib die Polung bei  und
und  an.
an.
c)
Bestimme die Zeitintervalle, in denen zwischen den Leiterenden  und
und  eine Spannung auftritt.
eine Spannung auftritt.
d)
Zeichne ein Zeit - Spannung - Diagramm für die Bewegung des Rahmens bis zum vollständigen Austritt aus dem Magnetfeld.
Das Experiment wird jetzt mit dem kurzgeschlossenen Rahmen (2) wiederholt. Dieser Rahmen besitzt einen elektrischen Widerstand von
e)
Erkläre, dass es sich hierbei nicht mehr um einen freien Fall handelt.
f)
Begründe rechnerisch, dass sich die Geschwindigkeit des Rahmens beim Eintritt in den Feldbereich verkleinert.
(12 VP)
3.
In einem Experiment wird eine Spule über einen Schalter an eine Gleichspannungsquelle von  angeschlossen. Die Spule hat einen elektrischen Widerstand von
angeschlossen. Die Spule hat einen elektrischen Widerstand von 
Parallel zu der Spule ist ein ohmscher Widerstand der Größe geschaltet.
geschaltet.
Die Stromstärke wird an zwei Stellen im Schaltkreis gemessen (siehe Abb. 3). Der zunächst offene Schalter wird geschlossen. Nach einiger Zeit wird eine konstante Stromstärke gemessen.
gemessen.
Parallel zu der Spule ist ein ohmscher Widerstand der Größe
Die Stromstärke wird an zwei Stellen im Schaltkreis gemessen (siehe Abb. 3). Der zunächst offene Schalter wird geschlossen. Nach einiger Zeit wird eine konstante Stromstärke
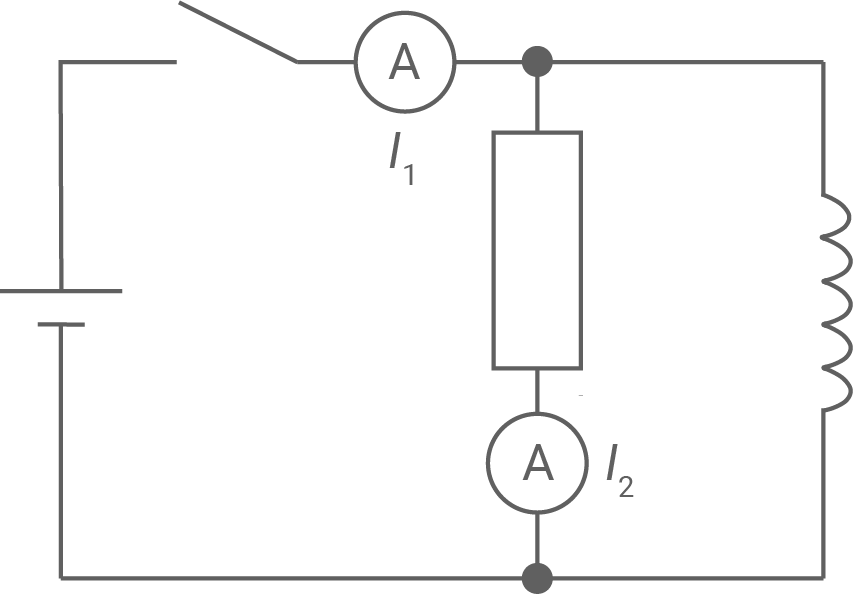
Abbildung 3
a)
Berechne die Stromstärke  .
.
Der Schalter wird zum Zeitpunkt 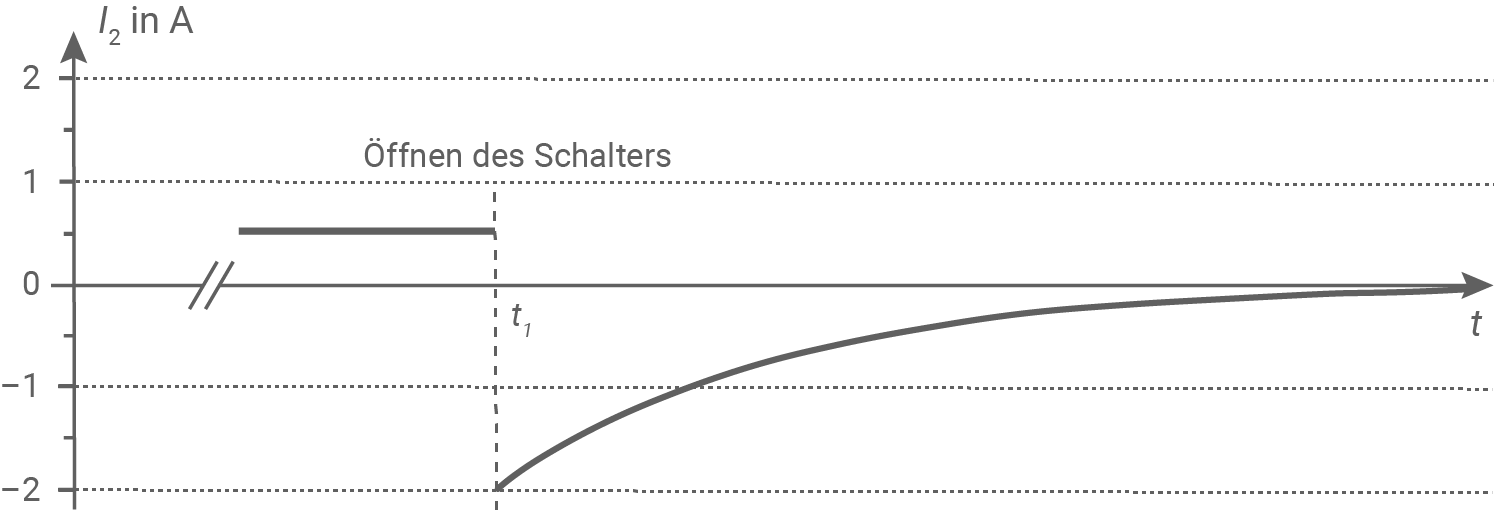
Abbildung 4
b)
Begründe die Änderung der Stromstärke bei 
c)
Bestimme die induzierte Spannung unmittelbar nach Öffnen des Schalters.
In der Spule befindet sich nun ein Eisenkern. Der Versuch wird wiederholt.
d)
Erläutere die Auswirkungen auf das Diagramm der Abbildung 
(9 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Dem Diagramm wird eine Schwingungsdauer von  entnommen. Die Schwingkreisfrequenz beträgt:
entnommen. Die Schwingkreisfrequenz beträgt:
![\(\begin{array}[t]{rll}
f &=& \dfrac{1}{T} \\[5pt]
f &=& \dfrac{1}{4 \mathrm{~ms}} \\[5pt]
f &=& 250 \mathrm{~Hz}
\end{array}\)](https://www.schullv.de/resources/formulas/abd8e26e846168cb8986d5143ff9c250fbe4be64d0ce55776df514363681f31c_light.svg)
b)
c)
Die maximale Stromstärke beträgt  Die maximale Energie im Magnetfeld beträgt
Die maximale Energie im Magnetfeld beträgt
![\(\begin{array}[t]{rll}
E_\text{max}&=& \dfrac{1}{2} \cdot L \cdot I_{\max }^{2} \\[5pt]
E_\text{max}&=& \dfrac{1}{2} \cdot 50 \mathrm{mH} \cdot(140 \mathrm{~mA})^{2} \\[5pt]
E_\text{max}&=& 490 \; \mu \mathrm{J} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1f1aead3d6a0755189abc6282f6575c76b0c6d768e89a42c53e84dc0afbf90bf_light.svg) Somit schwankt die magnetische Feldenergie zwischen Null und
Somit schwankt die magnetische Feldenergie zwischen Null und 
d)
Der Betrag der Stromstärke zur halben maximalen magnetischen Feldenergie ergibt sich aus folgender Gleichung:
![\(\begin{array}[t]{rll}
\dfrac{1}{2} \cdot E_\text{max}&=& \dfrac{1}{2} \cdot L \cdot I^{2} \\[5pt]
\dfrac{1}{2} \cdot E_\text{max} &=& \dfrac{1}{2} \cdot L \cdot I^{2} &\quad \scriptsize \mid\; \cdot \dfrac{2}{L} \\[5pt]
\dfrac{E_\text{max}}{L} &=& I^{2} &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{E_\text{max}}{L}} &=& I \\[5pt]
I &=& \sqrt{\dfrac{E_\text{max}}{L}} \\[5pt]
I &=& \sqrt{\dfrac{490 \; \mu \mathrm{J}}{50 \; \mathrm{mH}}} \\[5pt]
I &=& 99 \mathrm{~mA}
\end{array}\)](https://www.schullv.de/resources/formulas/7460712cf02a3b8ab6c395c0afb881bfb8ef3ab18068f55686958c211783ff80_light.svg) Aus der Abbildung 1 wird abgelesen, dass eine Stromstärke mit diesem Betrag erstmals zum Zeitpunkt
Aus der Abbildung 1 wird abgelesen, dass eine Stromstärke mit diesem Betrag erstmals zum Zeitpunkt  erreicht wird.
erreicht wird.
e)
Aus der maximalen elektrischen Feldenergie ergibt sich die maximale Spannung:
![\(\begin{array}[t]{rll}
E_\text{max} &=& \dfrac{1}{2} \cdot C \cdot U_{\max}{ }^{2} &\quad \scriptsize \mid\; \cdot \dfrac{2}{C} \\[5pt]
\dfrac{2 \cdot E_\text{max}}{C} &=& U_{\max}{ }^{2} &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{2 \cdot E_\text{max}}{C}} &=& U_{\max} \\[5pt]
U_{\max} &=& \sqrt{\dfrac{2 \cdot E_\text{max}}{C}} \\[5pt]
U_{\max} &=& \sqrt{\dfrac{2 \cdot 0,49 \mathrm{~mJ}}{8,1 \; \mu \mathrm{F}}} \\[5pt]
U_{\max} &=& 11 \mathrm{~V} \\[5pt]
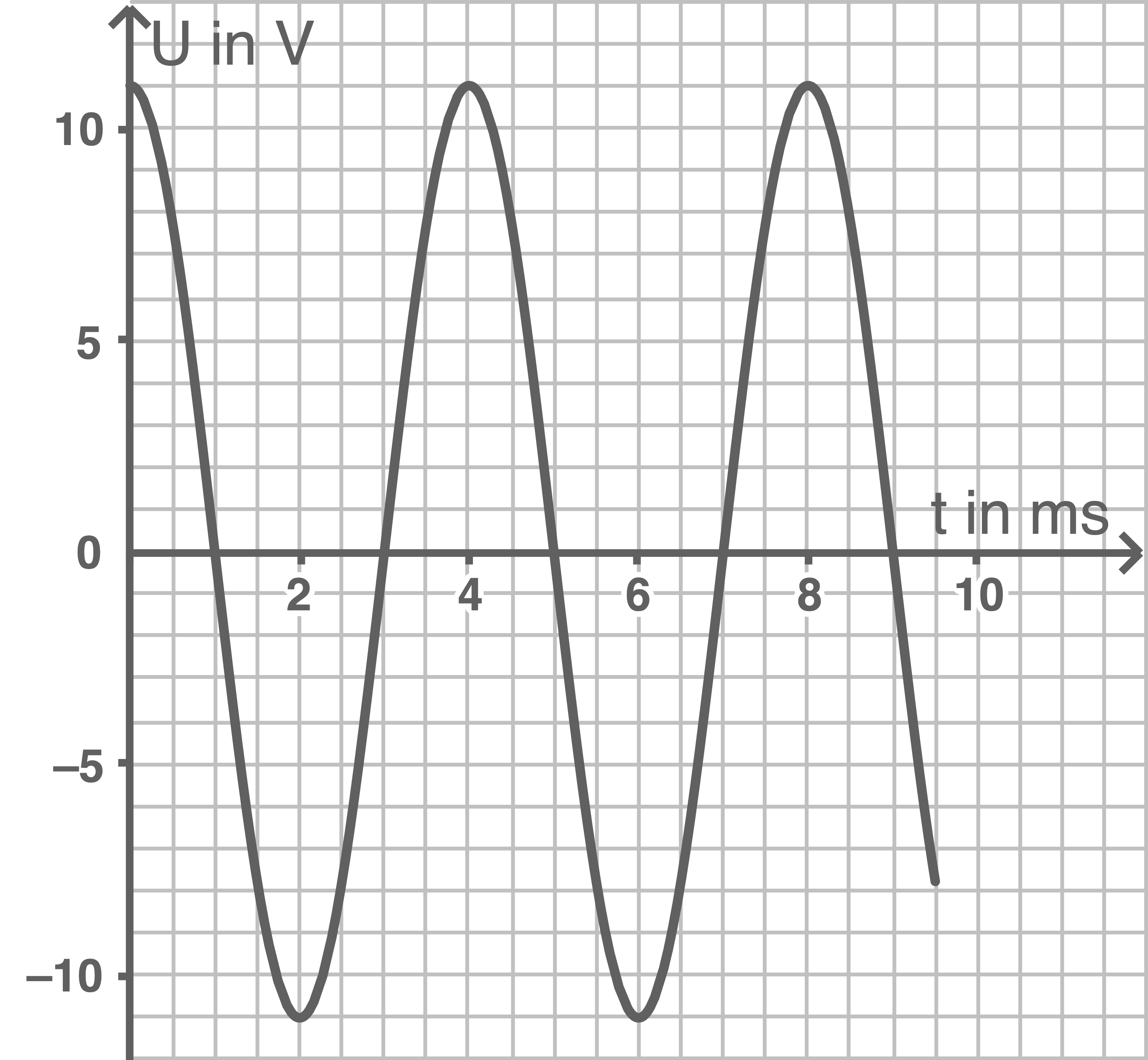
\end{array}\)](https://www.schullv.de/resources/formulas/4a13721211bf2f37923c4ab4df12a612653aa60b0413d6beca7386861f1fae8c_light.svg) Das Zeit-Spannungsdiagramm geht dem Zeit-Stromstärkendiagramm um eine viertel Periode voraus oder nach. Somit ergibt sich für das Zeit-Spannungsdiagramm:
Das Zeit-Spannungsdiagramm geht dem Zeit-Stromstärkendiagramm um eine viertel Periode voraus oder nach. Somit ergibt sich für das Zeit-Spannungsdiagramm:

2
a)
Sobald der untere Teil des Rahmens das Magnetfeld erreicht, wirkt auf die frei beweglichen Elektronen eine Lorentzkraft senkrecht zur Bewegungsrichtung und senkrecht zum Magnetfeld. In der Folge verschieben sich Elektronen im waagrechten Leiterstück nach links (Linke-Hand-Regel), in  entsteht ein Elektronenüberschuss und damit eine Spannung zwischen
entsteht ein Elektronenüberschuss und damit eine Spannung zwischen  und
und 
b)
Da die Elektronen sich aufgrund der Lorenzkraft im Leiterrahmen nach links verschieben, besteht in P ein Elektronenüberschuss (Minuspol) und in Q ein Elektronenmangel (Pluspol).
c)
1. Schritt: Eintrittzeitpunkts des Leiterrahmens in das Magnetfeld
Es gilt:
![\(\begin{array}[t]{rll}
s &=& \dfrac{1}{2} \cdot g \cdot t^2 &\quad \scriptsize \mid\; \cdot \dfrac{2}{g} \\[5pt]
\dfrac{2 \cdot s}{g} &=& t^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\dfrac{2 \cdot s}{g}} &=& t \\[5pt]
t &=& \sqrt{\dfrac{2 \cdot s}{g}} \\[5pt]
t &=& \sqrt{\dfrac{2 \cdot 5 \mathrm{~cm}}{9,81 \mathrm{~ms}^{-2}}} \\[5pt]
t &=& 0,10 \text{ s}
\end{array}\)](https://www.schullv.de/resources/formulas/ef5caebc13db9f1e75f3500e26fa7c36add1535e30e874a6d9a54ab86cf9dc7b_light.svg) 2. Schritt: Zeitpunkt zu dem der Leiterrahmen vollständig im Magnetfeld eingetaucht ist
2. Schritt: Zeitpunkt zu dem der Leiterrahmen vollständig im Magnetfeld eingetaucht ist
![\(\begin{array}[t]{rll}
t &=& \sqrt{\dfrac{2 \cdot s}{g}} \\[5pt]
t &=& \sqrt{\dfrac{2 \cdot 8 \mathrm{~cm}}{9,81 \mathrm{~ms}^{-2}}} \\[5pt]
t &=& 0,13 \text{ s}
\end{array}\)](https://www.schullv.de/resources/formulas/ab39c187eecbe84bd774c16fc4c251f41caf2a9f02f7814559a034153681c1c7_light.svg) 3. Schritt: Austrittzeitpunkts des Leiterrahmens aus dem Magnetfeld
3. Schritt: Austrittzeitpunkts des Leiterrahmens aus dem Magnetfeld
![\(\begin{array}[t]{rll}
t &=& \sqrt{\dfrac{2 \cdot s}{g}} \\[5pt]
t &=& \sqrt{\dfrac{2 \cdot 15 \mathrm{~cm}}{9,81 \mathrm{~ms}^{-2}}} \\[5pt]
t &=& 0,17 \text{ s}
\end{array}\)](https://www.schullv.de/resources/formulas/511f7fae025d59fd798cf993a95b3648468f5a9c4d88e975edf566357736c8a2_light.svg) 4. Schritt: Zeitpunkt zu dem der Leiterrahmen vollständig aus dem Magnetfeld ausgetreten ist
4. Schritt: Zeitpunkt zu dem der Leiterrahmen vollständig aus dem Magnetfeld ausgetreten ist
![\(\begin{array}[t]{rll}
t &=& \sqrt{\dfrac{2 \cdot s}{g}} \\[5pt]
t &=& \sqrt{\dfrac{2 \cdot 18 \mathrm{~cm}}{9,81 \mathrm{~ms}^{-2}}} \\[5pt]
t &=& 0,19 \text{ s}
\end{array}\)](https://www.schullv.de/resources/formulas/4b56abfe9f3f3bd41c731dafaf74c00247492feee24a8db1c1ff5c2e6a09c456_light.svg) 5. Schritt: Angabe der Zeitintervalle, in denen zwischen P und Q eine Spannung auftritt
Zwischen P und Q tritt eine Spannung auf, wenn sich die vom Magnetfeld durchdringte Fläche ändert. Dies ist bei Ein- und Austauchen der Fall. Somit ergeben sich die folgenden zwei Intervalle:
5. Schritt: Angabe der Zeitintervalle, in denen zwischen P und Q eine Spannung auftritt
Zwischen P und Q tritt eine Spannung auf, wenn sich die vom Magnetfeld durchdringte Fläche ändert. Dies ist bei Ein- und Austauchen der Fall. Somit ergeben sich die folgenden zwei Intervalle:
![\([0,10 \text{ s}; 0,13 \text{ s}]\)](https://www.schullv.de/resources/formulas/19f644eeb9e956cfd6a887df6b8c4aca4f1804fc72dc4cb7041bcf10b63bed08_light.svg) und
und ![\([0,17 \text{ s}; 0,19 \text{ s}]\)](https://www.schullv.de/resources/formulas/d0ecf34ecf4aecae90e75dda34cab5c971fed0abde354982d223a50fde9a9890_light.svg)
d)
Die Spannungen zu den Zeitpunkten 

 und
und  kann mit foldender Formel bestimmt werden
kann mit foldender Formel bestimmt werden
![\(\begin{array}[t]{rll}
U &=& B \cdot \ell \cdot v \\[5pt]
U &=& B \cdot \ell \cdot g \cdot t \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e2f1d83bc244ede7cd12b79dc5408362ca643fe6c7dcf3c804d90ba3c5139834_light.svg) Somit ergeben sich folgende Spannungen:
Somit ergeben sich folgende Spannungen:











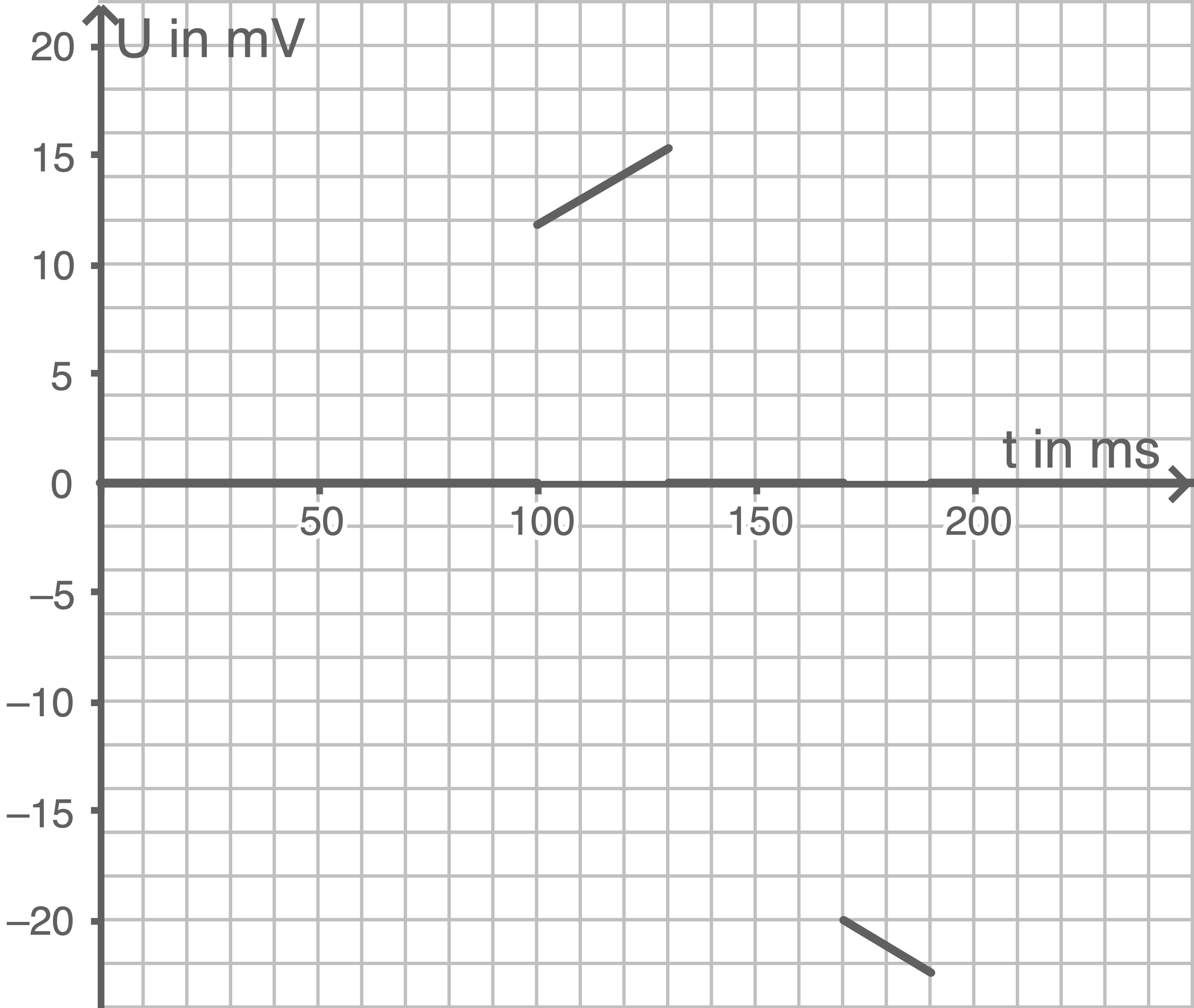
 Beim Feldeintritt bzw. beim Austritt besitzen die Spannungen unterschiedliche Vorzeichen, die Beträge der Spannungen steigen in den genannten Zeitintervallen linear an.
Beim Feldeintritt bzw. beim Austritt besitzen die Spannungen unterschiedliche Vorzeichen, die Beträge der Spannungen steigen in den genannten Zeitintervallen linear an.

e)
Sobald sich der magnetische Fluss im Rahmen (2) beim Eintreten und Verlassen des Felds ändert, wird im Rahmen ein Strom induziert. Nach Teilaufgabe a) fließt der Strom nach links. Nach der Linken-Hand-Regel erfährt der Leiterrahmen nun eine Lorenzkraft nach oben. Dadurch fälit der Rahmen (2) nicht frei.
f)
Beim Feldeintritt von Rahmen (2) wirken zwei Kräfte. Neben der beschleunigenden Gewichtskraft wirkt eine bremsende Kraft auf den stromdurchflossenen Leiter. Die Beschleunigung beträgt:
Da der Wert negativ ist, wird der Leiterrahmen im Moment des Feldeintritts gebremst. Die Geschwindigkeit wird kleiner.
3
a)
Längere Zeit nach Schließen des Schalters liegt sowohl am Widerstand als auch an der Spule die Spannung  an. Durch die Spule fließt ein Strom mit folgender Stärke:
an. Durch die Spule fließt ein Strom mit folgender Stärke:


 Durch den Widerstand fließt ein Strom mit folgender Stärke:
Durch den Widerstand fließt ein Strom mit folgender Stärke:


 Die Gesamtstromstärke
Die Gesamtstromstärke  beträgt somit
beträgt somit 
b)
Längere Zeit nach Schließen des Schalters wird im Widerstand die Stromstärke von  erreicht. Beim Öffnen des Schalters kann nur noch im rechten Teil der Schaltung ein Strom fließen. Angetrieben wird er durch die Induktionsspannung, die zwischen den Spulenenden entsteht. Sie ist so gerichtet, dass in der Spule anfangs weiterhin ein Strom von
erreicht. Beim Öffnen des Schalters kann nur noch im rechten Teil der Schaltung ein Strom fließen. Angetrieben wird er durch die Induktionsspannung, die zwischen den Spulenenden entsteht. Sie ist so gerichtet, dass in der Spule anfangs weiterhin ein Strom von  in die gleiche Richtung weiterfließt. Daher fließt der Strom im Widerstand nun entgegengesetzt zur ursprünglichen Richtung.
in die gleiche Richtung weiterfließt. Daher fließt der Strom im Widerstand nun entgegengesetzt zur ursprünglichen Richtung.
c)
Der Widerstand im Stromkreis hat insgesamt den Wert  , die Anfangsstromstärke in der Spule und im Widerstand beträgt
, die Anfangsstromstärke in der Spule und im Widerstand beträgt  . Die induzierte Spannung beim Ausschalten beträgt demnach
. Die induzierte Spannung beim Ausschalten beträgt demnach 
d)
Die Stromstärke vor dem Öffnen des Schalters beträgt nach wie vor  , unmittelbar nach dem Öffnen des Schalters fließt im Widerstand ein Strom der Stärke
, unmittelbar nach dem Öffnen des Schalters fließt im Widerstand ein Strom der Stärke  Nach der Maschenregel gilt:
Nach der Maschenregel gilt:
![\(\begin{array}[t]{rll}
0 \text{ V} &=& U_{i n d}+U_{R} \\[5pt]
0 \text{ V} &=& -L \cdot \dot{I}-R \cdot I &\quad \scriptsize \mid\; +R \cdot I \\[5pt]
R \cdot I &=& -L \cdot \dot{I} &\quad \scriptsize \mid\; :(-L) \\[5pt]
\dfrac{R \cdot I}{-L} &=& \dot{I} \\[5pt]
\dot{I} &=& \dfrac{R \cdot I}{-L} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f3ca597e933c76fcc3a4787107f282b56e033e1a7fb3a4b9668d18b18c474a03_light.svg) Da die Induktivität der eisengefüllten Spule größer ist und der Gesamtwiderstand
Da die Induktivität der eisengefüllten Spule größer ist und der Gesamtwiderstand  gleich bleibt, ist die momentane Änderungsrate zu jedem Zeitpunkt kleiner, d.h. die Stromstärke nimmt langsamer ab. Die Kurve wird flacher.
gleich bleibt, ist die momentane Änderungsrate zu jedem Zeitpunkt kleiner, d.h. die Stromstärke nimmt langsamer ab. Die Kurve wird flacher.