Aufgabe 2 – Licht
1.
Laserlicht der Wellenlänge  trifft senkrecht auf einen Doppelspalt. Parallel zur Doppelspaltebene befindet sich in
trifft senkrecht auf einen Doppelspalt. Parallel zur Doppelspaltebene befindet sich in  Entfernung ein Beobachtungsschirm. Abbildung 1 zeigt das Bedeutungsbild in Originalgröße.
Entfernung ein Beobachtungsschirm. Abbildung 1 zeigt das Bedeutungsbild in Originalgröße.




Abbildung 1
a)
Leite anhand geeigneter Skizzen Bedingungen für die Lage der Maxima auf dem Schirm her.
b)
Ermittle den Spaltmittenabstand des Doppelspaltes.
c)
Bestimme die Breite der einzelnen Spalte.
In einem weiteren Experiment wird der Doppelspalt durch andere Beugungsobjekte ersetzt. Auf dem Schirm beobachtet man nun die Beugungsbilder, die in Abbildung 2a und 2b in Originalgröße dargestellt sind.

Abbildung 2a

Abbildung 2b
d)
Erläutere, um welche Beugungsobjekte es sich dabei handeln könnte.
e)
Bestimme jeweils die charakteristische Größe dieser beiden Beugungsobjekte.
(11 VP)
2.
Das Licht einer Pflanzenleuchte erscheint pinkfarben.
In einem neuen Experiment fällt dieses Licht durch eine Spaltblende senkrecht auf ein Gitter mit der Gitterkonstanten Das Zentrum des Gitters befindet sich im Mittelpunkt eines kreisförmig gebogenen Schirms (siehe Abbildung 3). Es entsteht ein symmetrisches Interferenzmuster mit einem einzigen pinkfarbenen Streifen am Punkt
Das Zentrum des Gitters befindet sich im Mittelpunkt eines kreisförmig gebogenen Schirms (siehe Abbildung 3). Es entsteht ein symmetrisches Interferenzmuster mit einem einzigen pinkfarbenen Streifen am Punkt  und mehreren violetten und roten Streifen links und rechts davon.
und mehreren violetten und roten Streifen links und rechts davon.
In einem neuen Experiment fällt dieses Licht durch eine Spaltblende senkrecht auf ein Gitter mit der Gitterkonstanten
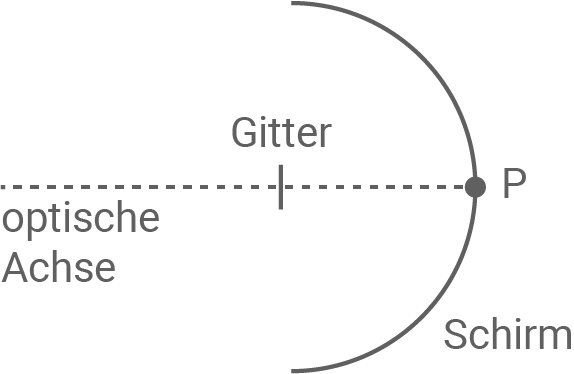
Abbildung 3
a)
Erkläre, warum auf dem Schirm drei verschiedene Farben zu sehen sind.
Das violette Licht hat eine Wellenlänge von
b)
Bestimme die Beugungswinkel der beiden zugehörigen violetten Helligkeitsmaxima.
Nun wird ein anderes Gitter verwendet. Auf dem Schirm ist nur der pinkfarbene Streifen beobachtbar.
c)
Bestimme einen Bereich für die Gitterkonstante dieses Gitters.
In einem neuen Experiment wird das Gitter durch einen Einzelspalt ersetzt. An den beiden äußeren Rändern des pinkfarbenen Streifens kann nun ein anderer Farbeindruck entstehen.
d)
Nenne eine mögliche Ursache für diesen Effekt.
Abbildung 4 zeigt, wie stark ein Pflanzenblatt Licht in Abhängigkeit von der Energie der Photonen absorbiert.
e)
Erläutere, warum das Licht der verwendeten Pflanzenleuchte für die Absorption besonders geeignet ist.
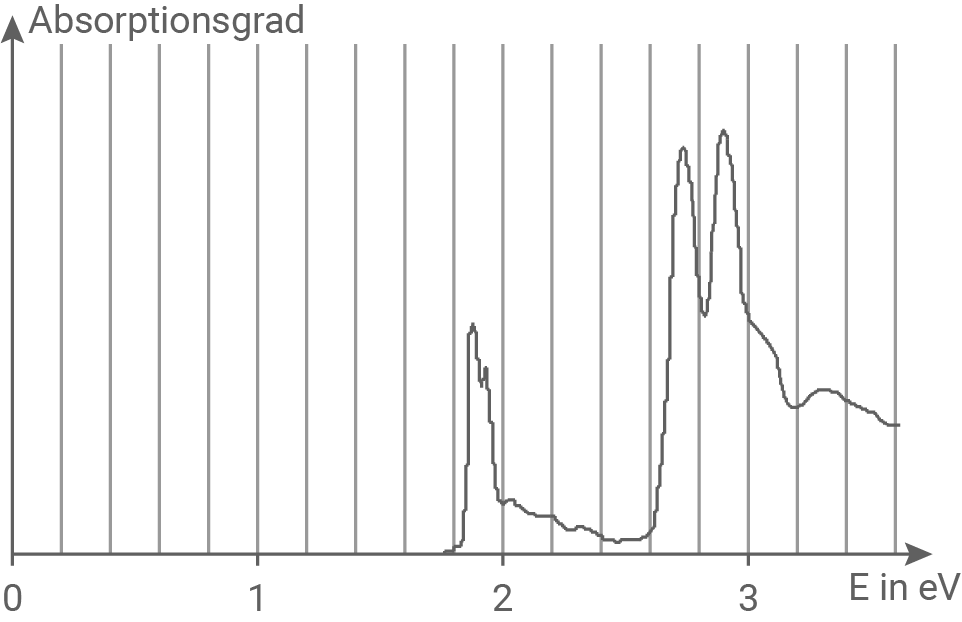
Abbildung 4
3.
Einzelne Elektronen treffen mit der Geschwindigkeit  senkrecht auf einen Doppelspalt. Hinter dem Doppelspalt befindet sich parallel dazu ein Detektionsschirm, der nach längerer Zeit die Verteilung in Abbildung 5 zeigt.
senkrecht auf einen Doppelspalt. Hinter dem Doppelspalt befindet sich parallel dazu ein Detektionsschirm, der nach längerer Zeit die Verteilung in Abbildung 5 zeigt.
a)
Erläutere, warum Elektronen ein Interferenzmuster erzeugen können.

Abbildung 5
b)
Berechne die Wellenlänge, die den Elektronen unter Berücksichtigung des relativistischen Effektes zugeordnet werden kann.
c)
Vergleiche die Lage der Maxima in der Abbildung mit denen in einer theoretischen Intensitätsverteilung, die sich ohne den relativistischen Effekt ergäbe.
1.
a)
Entstehung des Interferenzbildes
Die Entstehung des Interferenzbildes auf dem Schirm erfolgt aufgrund der Beugung des monochromatischen Lichts an den beiden schmalen Spalten im Doppelspalt.
Wenn Licht auf die Spalte trifft, werden die einzelnen Spalte zu neuen Quellen von Elementarwellen, die sich in alle Richtungen ausbreiten. Diese Elementarwellen überlagern sich auf dem Schirm, und an bestimmten Stellen interferieren sie konstruktiv, was zu hellen Streifen führt, während an anderen Stellen destruktive Interferenz auftritt, was zu dunklen Streifen führt.
Bedingungen für die Lage der Maxima
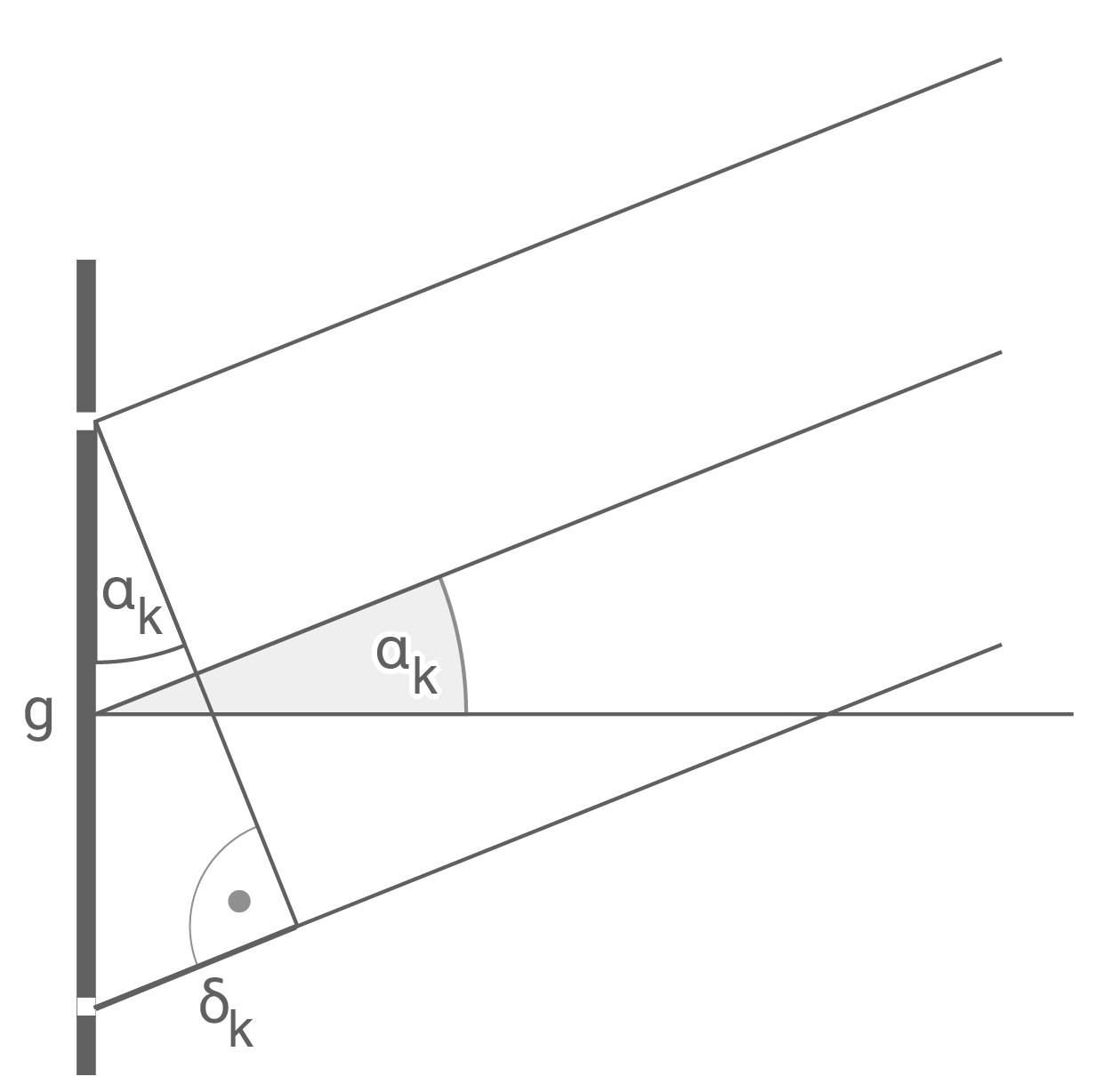 Es gilt:
Es gilt:  Für
Für  entstehen Intensitätsmaxima und für
entstehen Intensitätsmaxima und für  entstehen Intensitätsminima für
entstehen Intensitätsminima für  Für Winkel mit
Für Winkel mit  entstehen Maxima, die Minima liegen dazwischen.
entstehen Maxima, die Minima liegen dazwischen.
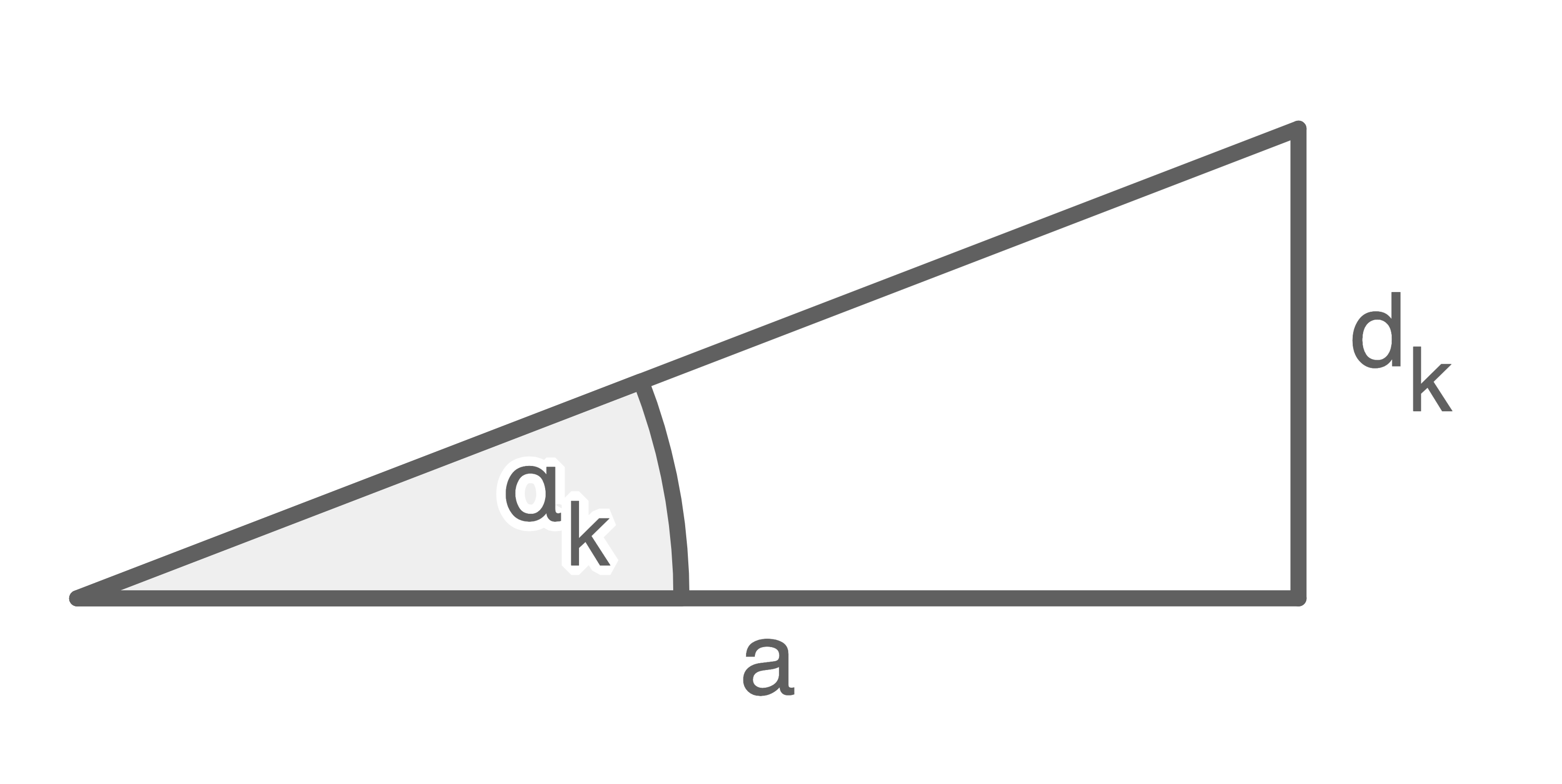

Die Abstände  der Maxima vom Maximum 0. Ordnung lassen sich mit
der Maxima vom Maximum 0. Ordnung lassen sich mit  berechnen.
berechnen.  entspricht dem Abstand des Schirms zum Doppelspalt.
entspricht dem Abstand des Schirms zum Doppelspalt.

b)
Für kleine Winkel  gilt:
gilt:
![\(\begin{array}[t]{rll}
\sin (\alpha_k)&=& \tan (\alpha_k) \\[5pt]
\dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a} &\quad \scriptsize \mid\;\cdot a \\[5pt]
\dfrac{k \cdot \lambda}{g}\cdot a&=& d_k \\[5pt]
d_k &=& k\cdot \dfrac{\lambda \cdot a}{g}
\end{array}\)](https://www.schullv.de/resources/formulas/87858f3f9e35ddb457143155293336c3527c8c1a93d2d53abc8e04464d03c5eb_light.svg) Spaltmittenabstand berechnen
Es wird die Kleinwinkelnäherung angewandt, da die Winkel klein sind. Für das Maximum 1. Ordnung gilt
Spaltmittenabstand berechnen
Es wird die Kleinwinkelnäherung angewandt, da die Winkel klein sind. Für das Maximum 1. Ordnung gilt  (siehe Abbildung 1).
(siehe Abbildung 1).
![\(\begin{array}[t]{rll}
d_k&=& \dfrac{k \cdot \lambda}{g}\cdot a &\quad \scriptsize \mid\;\cdot g \;\mid\;:d_k \\[5pt]
g&=& \dfrac{k \cdot \lambda\cdot a}{d_k}\\[5pt]
g&=& \dfrac{6,33 \cdot 10^{-7} \mathrm{~m} \cdot 1\cdot 3,50 \mathrm{~m}}{1,1 \cdot 10^{-2} \mathrm{~m}}\\[5pt]
g&=& 0,20 \mathrm{~mm}
\end{array}\)](https://www.schullv.de/resources/formulas/0de43ef850b58ab5d0db7003606f3c61e26adc697e4370bac6ccd84141d48553_light.svg)
c)
In Abbildung 1 ist zu sehen, dass die Maxima 2. Ordnung ausfallen, da auf die Stellen die Minima 1. Ordunung der Einzelspaltbeugung fallen.
Für die Beugungswinkel der Minima erster Ordung der Einzelspalte gilt:
 für
für  Gleichsetzen der Beugungsformeln:
Gleichsetzen der Beugungsformeln:
![\(\begin{array}[t]{rll}
\sin(\beta_1)&=& \sin (\alpha_2) \\[5pt]
\dfrac{1 \cdot \lambda}{b}&=& \dfrac{2 \cdot \lambda}{g} &\quad \scriptsize \mid\;\cdot b \; \mid\;\cdot \dfrac{g}{2 \cdot \lambda}\\[5pt]
\dfrac{g}{2}&=& b \\[5pt]
b&=& \dfrac{g}{2} \\[5pt]
b&=&\dfrac{0,2\;\text{mm}}{2}\\[5pt]
&=& 0,1\;\text{mm}
\end{array}\)](https://www.schullv.de/resources/formulas/c11b0665656e7821371d6e61c342896ddec76a6d2a2a1be3c9c7f05d0937ed38_light.svg)
d)
Beim zur Abbildung 2a gehörenden Beugungsobjekt könnte es sich um einen Einzelspalt handeln. Der zentrale helle Fleck ist deutlich breiter und heller im Vergleich zu den weiteren hellen Flecken, deren Intensität mit zunehmender Ordnung stark abnimmt.
Das Beugungsobjekt, das zu Abbildung \(2 b\) gehört, ist vermutlich ein Gitter bzw. ein Mehrfachspalt mit einer großen Anzahl von ausgeleuchteten Spaltöffnungen. Die Maxima sind scharf begrenzt, die Bereiche dazwischen sind nahezu dunkel.
Das Beugungsobjekt, das zu Abbildung \(2 b\) gehört, ist vermutlich ein Gitter bzw. ein Mehrfachspalt mit einer großen Anzahl von ausgeleuchteten Spaltöffnungen. Die Maxima sind scharf begrenzt, die Bereiche dazwischen sind nahezu dunkel.
e)
In der Abbildung 2 a liegt das Minimum 2. Ordnung bei  .
Für die Minima 2. Ordnung gilt hier:
.
Für die Minima 2. Ordnung gilt hier: 
 .
Die Breite des Einzelspalts beträgt somit:
.
Die Breite des Einzelspalts beträgt somit:


 In der Abbildung 2b liegt das Maximum 2 . Ordnung bei
In der Abbildung 2b liegt das Maximum 2 . Ordnung bei  .
Für die Maxima 2. Ordnung gilt hier:
.
Für die Maxima 2. Ordnung gilt hier: 
 .
Die Gitterkonstante beträgt:
.
Die Gitterkonstante beträgt:


 .
.
2.
a)
Das pinkfarbene Licht der Pflanzenleuchte besteht aus einem violetten und einem roten Farbanteil. Da rotes und violettes Licht unterschiedliche Wellenlängen haben, werden diese verschieden stark am Gitter gebeugt. Lediglich das Maximum 0. Ordung der beiden fällt zusammen. Somit ist das Maximum 0. Ordung pink. Alle anderen Maxima sind entweder rot oder violett.
b)
Formel für die Maxima:  .
Berechnung des Beugungswinkels für das erste violette Maximum ergibt:
.
Berechnung des Beugungswinkels für das erste violette Maximum ergibt:
 . Somit ist
. Somit ist  Berechnen weiterer Beugungswinkel für rot und violett ergibt:
Berechnen weiterer Beugungswinkel für rot und violett ergibt:
Zwischen den Maxima zweiter und dritter Ordnung des violetten Lichts liegen keine Maxima roten Lichts. Somit sind die beiden gesuchten Beugungswinkel:  und
und  .
.
| k | violett | rot |
|---|---|---|
| 0 | 0 | 0 |
| 1 | ||
| 2 | ||
| 3 |
c)
Damit auf dem Schirm nur der pinkfarbene Streifen sichtbar ist, dürfen keine roten oder violetten Maxima mehr auftreten. Da violettes Licht die kleinere Wellenlänge hat und somit seine Beugungswinkel im Vergleich zu den Beugungswinkeln des roten Lichts geringer ausfallen, muss gelten:
 Somit muss
Somit muss 
 sein.
sein.
d)
Das zentrale Maximum auf dem Schirm ist bei der Ausleuchtung des Spalts mit violettem Licht schmaler als bei Verwendung roten Lichtes. Die Ränder des Maximums nullter Ordnung erscheinen daher bei der Beleuchtung mit der hier benutzten Pflanzenleuchte in einer Mischfarbe, bei denen verschiedene Intensitäten von violett und rot vermischt werden.
e)
Berechnen der beiden Photenenenergie ergibt:









 In den Diagramm sind drei Energiemaxima ablesbar.
In den Diagramm sind drei Energiemaxima ablesbar.  stimmt mit dem dritten Energiemaximum überein und
stimmt mit dem dritten Energiemaximum überein und  stimmt mit dem ersten Energiemaximum überein. Das Pflanzenblatt absorbiert also diese Energien besonders gut.
Die Lampe sendet Licht aus, das vom Pflanzenblatt gut aufgenommen werden kann.
stimmt mit dem ersten Energiemaximum überein. Das Pflanzenblatt absorbiert also diese Energien besonders gut.
Die Lampe sendet Licht aus, das vom Pflanzenblatt gut aufgenommen werden kann.
3
a)
Elektronen sind Quantenobjekte, denen eine Wellenlänge zuordnen werden kann (De Broglie). Am Doppelspalt findet Beugung statt. Auf dem Schirm entsteht eine aus der Wahrscheinlichkeitswelle vorausberechenbare Intensitätsverteilung mit Orten hoher und niedriger Auftreffwahrscheinlichkeit. Die weißen Streifen sind in der Abbildung Zonen mit hoher Auftreffwahrscheinlichkeit.
b)
Die Masse der bewegten Elektronen lässt sich mit der gegebenen Formel berechnen:
![\(\begin{array}[t]{rll}
m&=& \dfrac{m_{0}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}} \\[5pt]
&=&\dfrac{9,11 \cdot 10^{-31}}{\sqrt{1-\dfrac{1,46^{2}}{3,00^{2}}}} \mathrm{~kg} \\[5pt]
&=&1,04 \cdot 10^{-30} \mathrm{~kg}
\end{array}\)](https://www.schullv.de/resources/formulas/74f321a886737bf9ae427f176fe4c388017c766a2bdfcc2a02618f7f297244b8_light.svg) Die Wellenlänge kann mit der de Broglie-Wellenlängen Formel berechnet werden:
Die Wellenlänge kann mit der de Broglie-Wellenlängen Formel berechnet werden:
![\(\begin{array}[t]{rll}
\lambda&=& \dfrac{h}{m \cdot v} \\[5pt]
&=&\dfrac{6,63 \cdot 10^{-34} \mathrm{Js}}{1,04 \cdot 10^{-30} \mathrm{~kg} \cdot 1,46 \cdot 10^{8} \mathrm{~ms}^{-1}} \\[5pt]
&=&4,37 \cdot 10^{-12} \mathrm{~m}
\end{array}\)](https://www.schullv.de/resources/formulas/447b2ace2831676d37555507e4096c11b2ba269703adf928eaa650fdb6e0602f_light.svg)
c)
Die Ruhemasse eines Elektrons ist geringer als die berechnete Masse eines bewegten Elektrons. Somit ist die de Broglie-Wellenlänge größer, da  .
Anhand der Formel für Beugungswinkel der Maxima
.
Anhand der Formel für Beugungswinkel der Maxima 
 ist ersichtlich, dass die Maxima näher zusammenrücken, je kleiner die Wellenlänge
ist ersichtlich, dass die Maxima näher zusammenrücken, je kleiner die Wellenlänge  wird.
Somit sind in der theoretischen Intensitätsverteilung die Streifenabstände größer.
wird.
Somit sind in der theoretischen Intensitätsverteilung die Streifenabstände größer.