Aufgabe 1 – Mechanische Schwingungen
1.
In der Schwerelosigkeit können Astronauten ihre Masse mit der in Abbildung 1 dargestellten Anordnung bestimmen. Der Astronaut setzt sich dazu in einen Stuhl, der die Masse  hat und zwischen zwei Federn eingespannt ist. Der Stuhl wird um
hat und zwischen zwei Federn eingespannt ist. Der Stuhl wird um  aus der Gleichgewichtslage ausgelenkt und zum Zeitpunkt
aus der Gleichgewichtslage ausgelenkt und zum Zeitpunkt  frei gegeben. Die Anordnung schwingt harmonisch mit einer Richtgröße
frei gegeben. Die Anordnung schwingt harmonisch mit einer Richtgröße  von
von  Von Reibung und von der Federmasse wird abgesehen.
Von Reibung und von der Federmasse wird abgesehen.
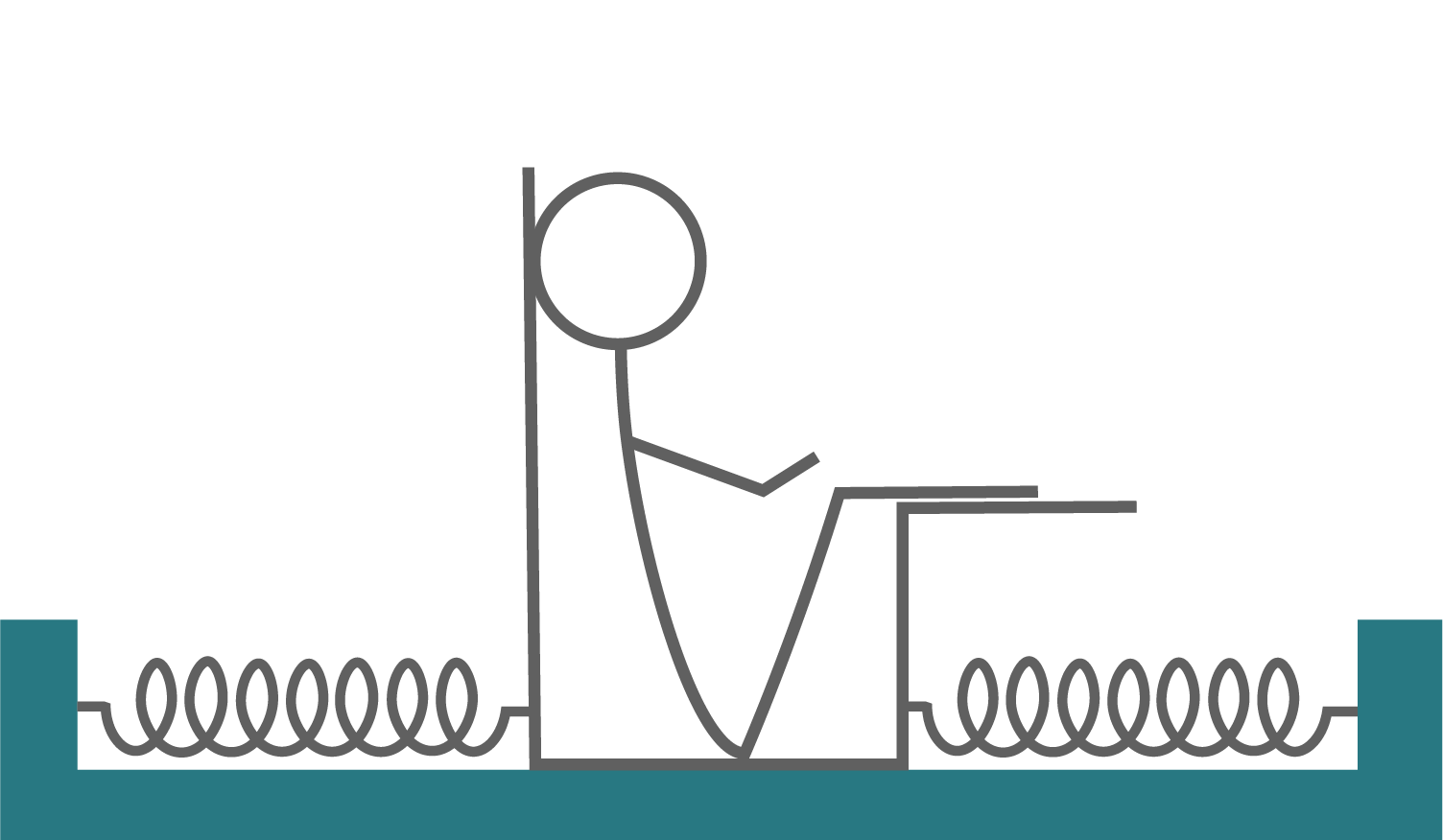
Abbildung 1
a)
Gib für diese Messung eine Funktionsgleichung an, die die Auslenkung des Stuhls aus der Gleichgewichtslage in Abhängigkeit von der Zeit beschreibt.
b)
Berechne die Masse des Astronauten.
c)
Zeichne das Zeit-Geschwindigkeit-Diagramm für die ersten drei Sekunden der Messung.
d)
Beschreibe, wie sich in diesem Experiment eine größere Masse des Astronauten auf das Zeit-Geschwindigkeit-Diagramm auswirkt.
e)
Vergleiche die maximale Beschleunigung des Astronauten auf dem Stuhl mit der Erdbeschleunigung.
(10 VP)
2.
Das linke Ende eines  langen elastischen Bandes beginnt zum Zeitpunkt
langen elastischen Bandes beginnt zum Zeitpunkt  harmonisch zu schwingen. Dadurch wird auf dem Band eine Welle erzeugt, die sich nach rechts ausbreitet. Das rechte Ende des Bandes ist fest.
harmonisch zu schwingen. Dadurch wird auf dem Band eine Welle erzeugt, die sich nach rechts ausbreitet. Das rechte Ende des Bandes ist fest.
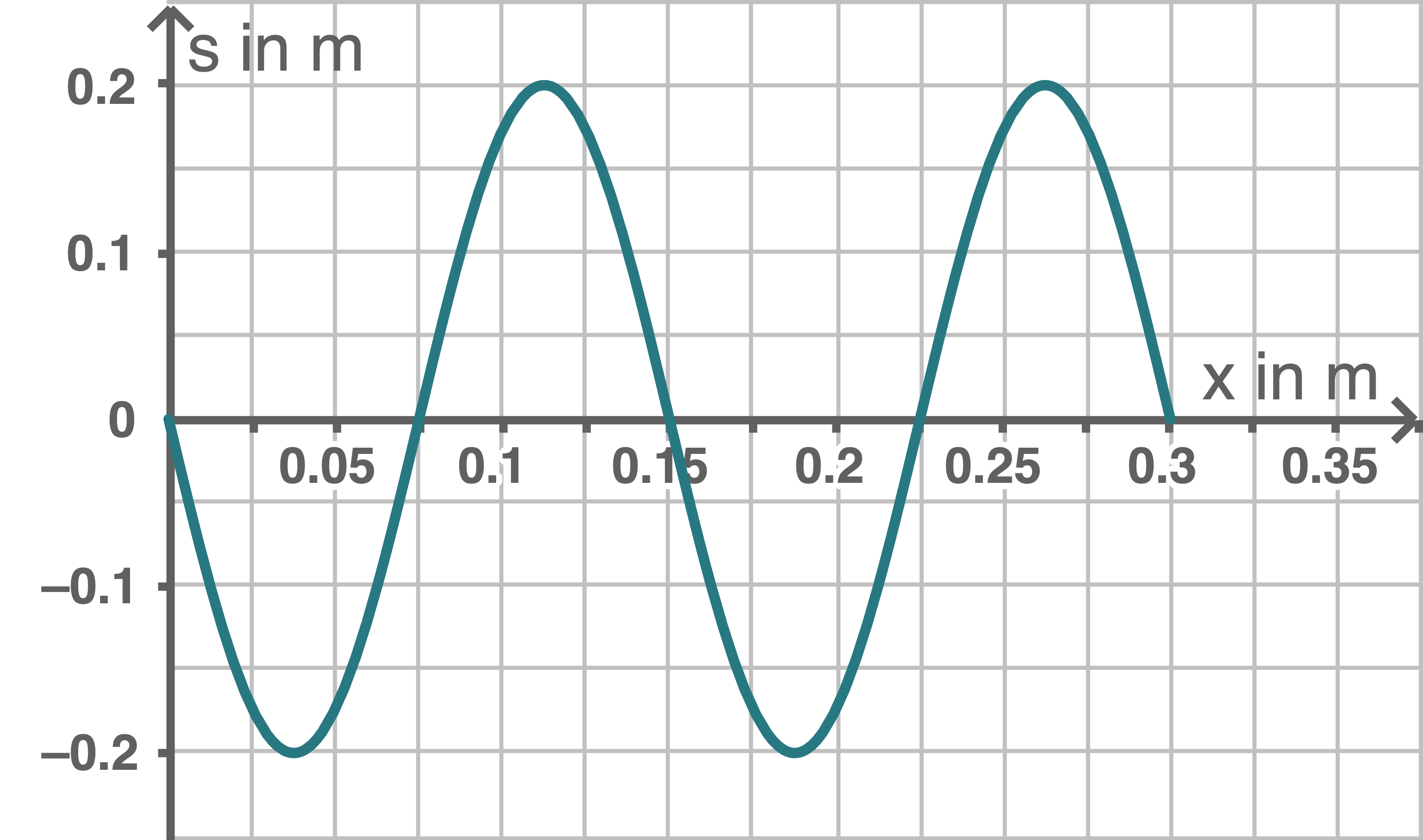
Abbildung 2 zeigt den zeitlichen Verlauf der Auslenkung eines Punktes, der vom linken Ende des Bandes entfernt ist.
vom linken Ende des Bandes entfernt ist.
Abbildung 2 zeigt den zeitlichen Verlauf der Auslenkung eines Punktes, der
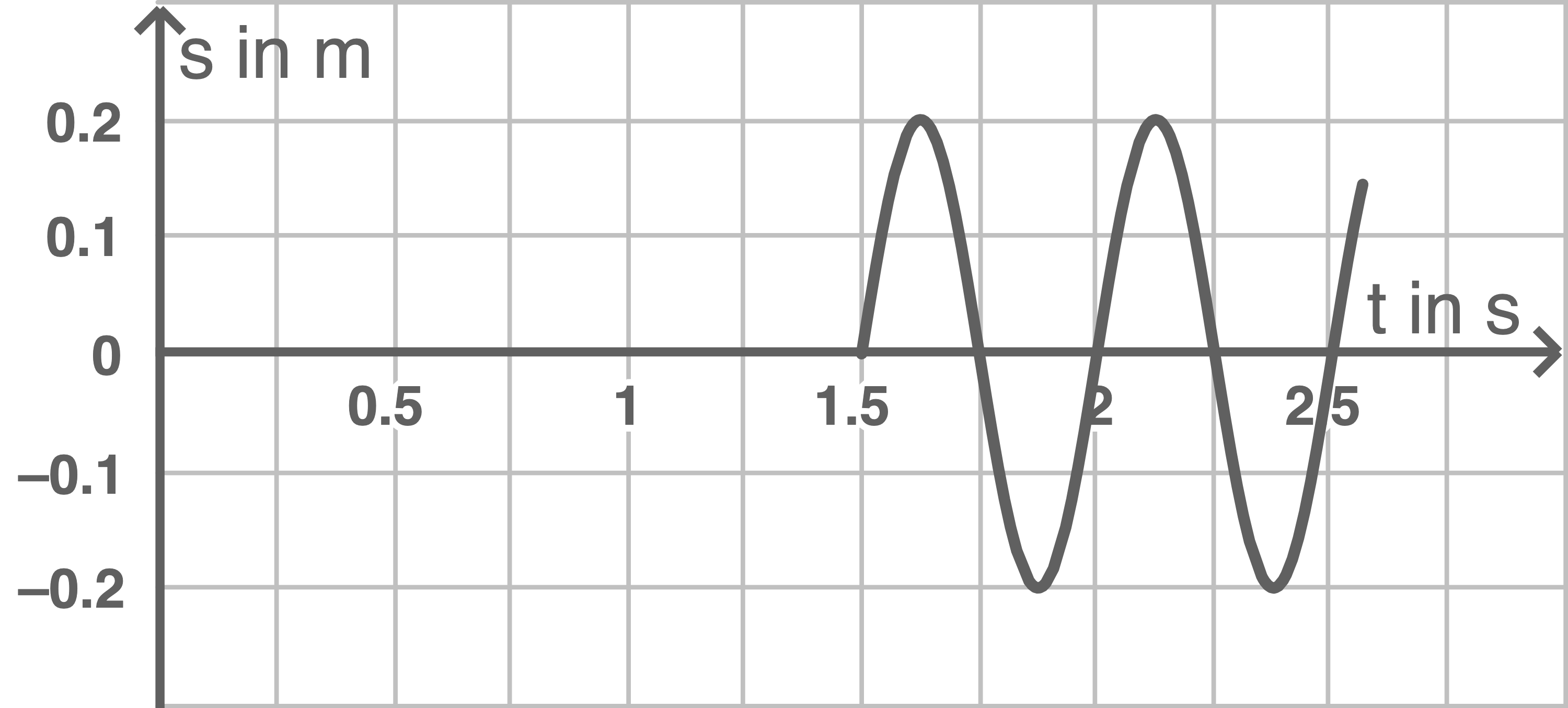
Abbildung 2
a)
Berechne die Ausbreitungsgeschwindigkeit der Welle.
b)
Skizziere das Momentanbild des gesamten Bandes zum Zeitpunkt 
c)
Zeichne für den Zeitraum von  das Zeit-Auslenkungs-Diagramm für denjenigen Punkt, der
das Zeit-Auslenkungs-Diagramm für denjenigen Punkt, der  vom linken Ende des Bandes entfernt ist.
vom linken Ende des Bandes entfernt ist.
Das linke Ende eines weiteren elastischen Bandes wird über eine Umlenkrolle geführt und gespannt (siehe Abbildung 3). Das Band wird mit einer festen Frequenz von  zu Schwingungen angeregt. In einem Experiment wird die Spannkraft
zu Schwingungen angeregt. In einem Experiment wird die Spannkraft  verändert und gemessen, bei welchen Werten von
verändert und gemessen, bei welchen Werten von  stehende Wellen auftreten. Dabei ist
stehende Wellen auftreten. Dabei ist  die Anzahl der Schwingungsbäuche der stehenden Welle. Die Ergebnisse sind in Tabelle 1 dargestellt.
die Anzahl der Schwingungsbäuche der stehenden Welle. Die Ergebnisse sind in Tabelle 1 dargestellt.
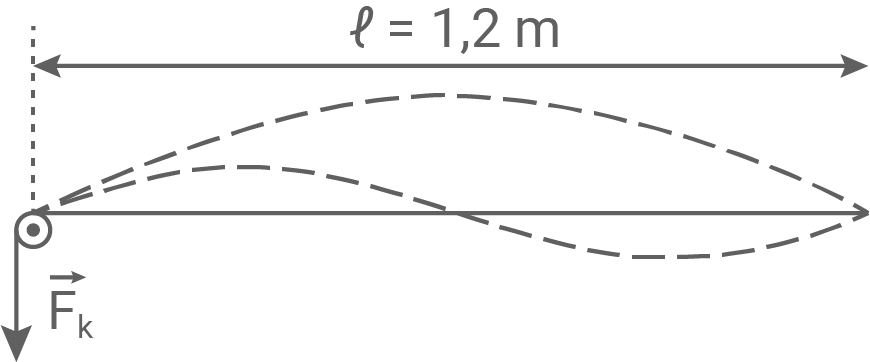
Abbildung 3
Tabelle 1
d)
Zeige, dass die Beziehung  gilt.
gilt.
e)
Bestimme den zugehörigen Proportionalitätsfaktor unter Verwendung der Messwerte aus Tabelle 1.
Für die Spannkraft gilt:
f)
Bestimme die Masse des Bandes.
(11 VP)
3.
Im Jahr 1905 erklärte Albert Einstein den Fotoeffekt mithilfe einer Hypothese, die Max Planck in der Fachwelt bereits im Jahr 1900 aufgestellt hatte. Einstein kam in diesem Zusammenhang zu der folgenden Gleichung:

 und
und  bei konstanter Frequenz
bei konstanter Frequenz  dargestellt.
dargestellt.
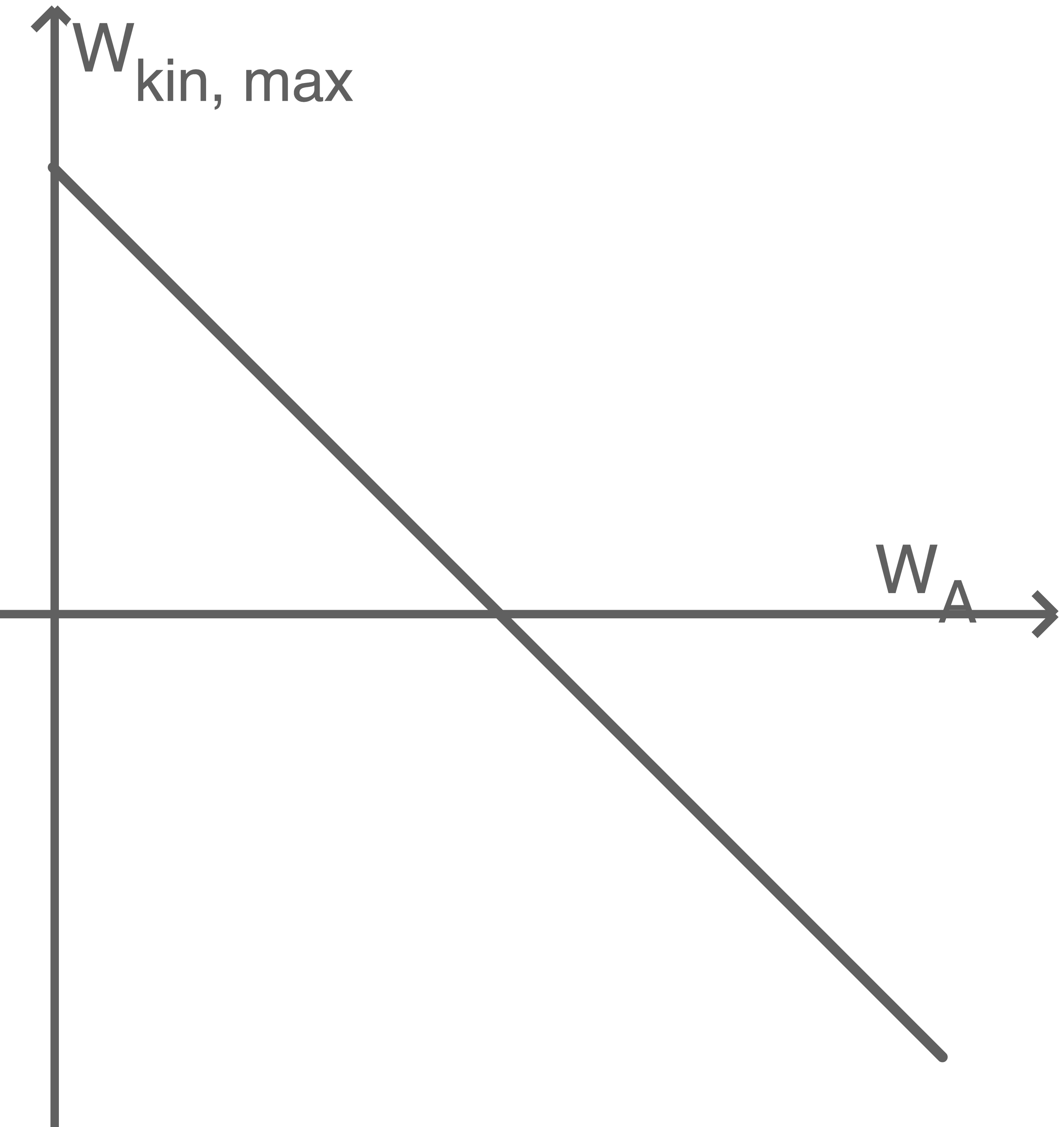
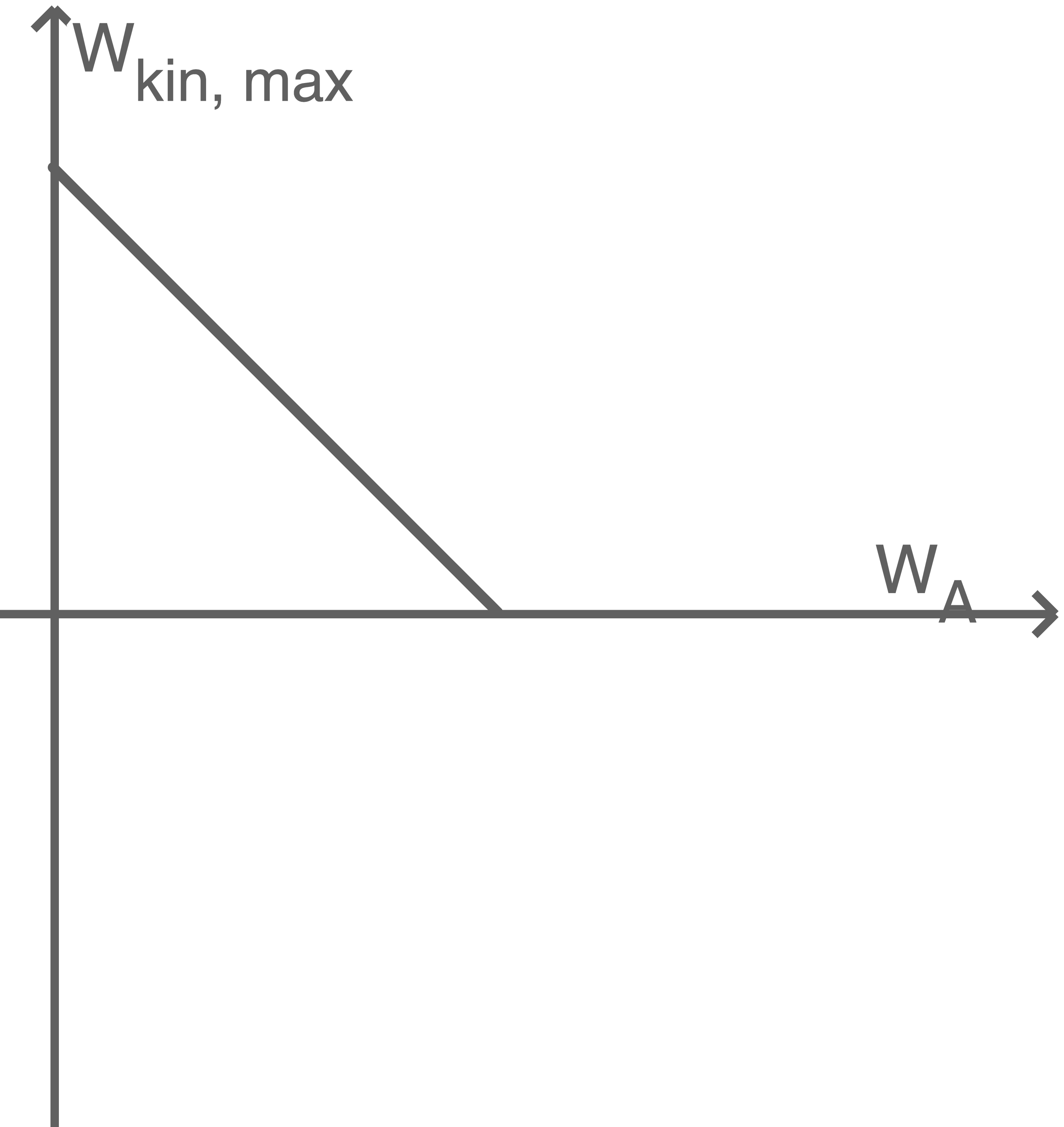
a)
Erläutere die physikalische Aussage dieser Gleichung.
In einem der drei Diagramme aus den Abbildungen 4a bis 4c ist der Zusammenhang zwischen 
Abbildung 4 a

Abbildung 4 c

Abbildung 4 b
b)
Gib an, welches der Diagramme diesen Zusammenhang am besten darstellt und begründe deine Wahl.
c)
Beschreibe, wie man den  -
- -Zusammenhang experimentell überprüfen kann.
-Zusammenhang experimentell überprüfen kann.
d)
Erläutere den Aspekt des Fotoeffekts, der mit der klassischen Vorstellung von elektromagnetischen Wellen nicht vereinbar ist.
(9 VP)
1.
a)
Die allgemeine Auslenkung des Stuhls aus der Gleichgewichtslage in Abhängigkeit von der Zeit kann als Bewegungsgleichung beschrieben werden, mittels:
 Hier gilt
Hier gilt  Für zehn Schwingungsperioden wird eine Zeit von
Für zehn Schwingungsperioden wird eine Zeit von  gemessen, also ergibt sich die Periodendauer
gemessen, also ergibt sich die Periodendauer  aus der Zeit der Schwingungsdauer.
aus der Zeit der Schwingungsdauer.
 Es ist
Es ist  Somit folgt die Funktionsgleichung für
Somit folgt die Funktionsgleichung für  mit
mit 
b)
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
1. Schritt: Masse des schwingenden Systems bestimmen
Lösung:
1. Schritt: Masse des schwingenden Systems bestimmen
![\(\begin{array}[t]{rll}
T&=& 2 \pi \cdot \sqrt{\dfrac{m}{D}}&\quad \scriptsize \mid\; (\;)^2\\[5pt]
T^2&=& 4 \pi^2 \cdot \dfrac{m}{D} &\quad \scriptsize \mid\;\cdot \dfrac{D}{4 \pi^2} \\[5pt]
T^2 \cdot \dfrac{D}{4 \pi^2}&=& m \\[5pt]
m &=& T^2 \cdot \dfrac{D}{4 \pi^2} \\[5pt]
m &=& (1,5 \;\text{s})^2 \cdot \dfrac{1500 \;\frac{\text{N}}{\text{m}}}{4 \pi^2} \\[5pt]
m &=& 85,5 \; \text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/519cfe245e2fe3a65bcdbf7c4b74a5e7f55759e9086c1124175dae6321150a08_light.svg) 2. Schritt: Masse des Astronauten berechnen
Die Masse des Astronauten beträgt
2. Schritt: Masse des Astronauten berechnen
Die Masse des Astronauten beträgt 

c)
Die Geschwindigkeit ergibt sich durch Ableiten von  nach der Zeit.
1. Schritt: Ableitung bilden
Es gilt:
nach der Zeit.
1. Schritt: Ableitung bilden
Es gilt: 

 Somit folgt die Zeit-Geschwindigkeit-Funktion zu
Somit folgt die Zeit-Geschwindigkeit-Funktion zu  2. Schritt: Zeit-Geschwindigkeit-Diagramm
2. Schritt: Zeit-Geschwindigkeit-Diagramm
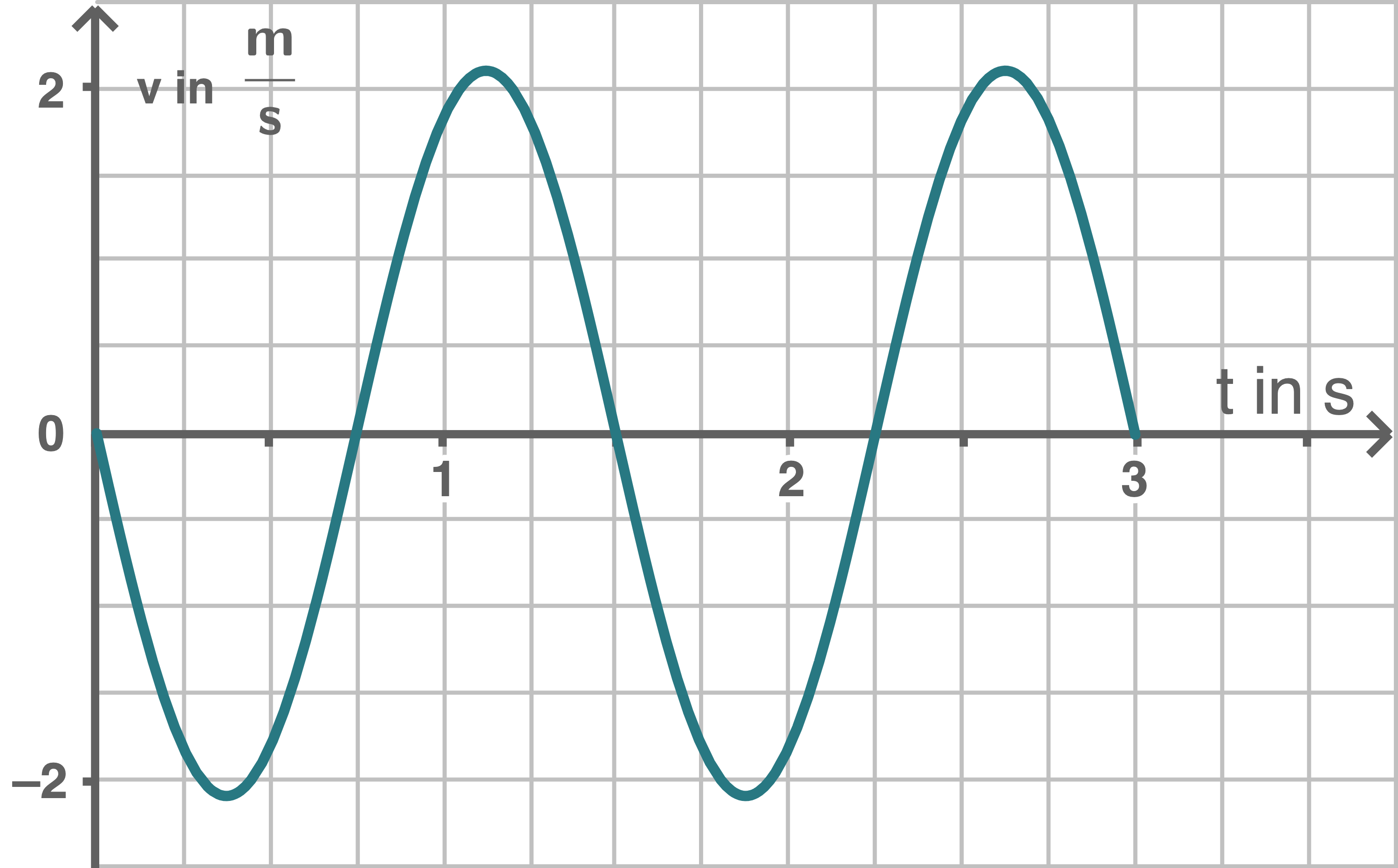

d)
Es ist  Vergrößert sich die Masse
Vergrößert sich die Masse  so wird auch
so wird auch  größer.
Wegen
größer.
Wegen  wird die Kreisfrequenz kleiner.
Somit verringert sich auch die maximale Geschwindigkeit. Das Diagramm wird folglich in
wird die Kreisfrequenz kleiner.
Somit verringert sich auch die maximale Geschwindigkeit. Das Diagramm wird folglich in  -Richtung gestreckt und in
-Richtung gestreckt und in  -Richtung gestaucht.
-Richtung gestaucht.
e)
Die maximale Beschleunigung des Systems ergibt sich zu:


 Die maximale Beschleunigung des Systems ist folglich kleiner als die Erdbeschleunigung
Die maximale Beschleunigung des Systems ist folglich kleiner als die Erdbeschleunigung 
2.
a)
Das Teilchen beginnt zum Zeitpunkt  zu schwingen und befindet sich zum Zeitpunkt
zu schwingen und befindet sich zum Zeitpunkt  am Ort
am Ort  Gegeben:
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
Lösung: 

b)
Die Periodendauer wird aus Abbildung 2 ablesen. Sie beträgt  Nach einer Sekunde hat sich die Welle folglich um
Nach einer Sekunde hat sich die Welle folglich um 

 augebreitet.
Die Wellenlänge ergibt sich zu:
augebreitet.
Die Wellenlänge ergibt sich zu:


c)
Zeitpunkt zu dem die Schwingung beginnt
Gegeben: 

 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
t&=& \dfrac{x}{c} \\[5pt]
t&=& \dfrac{1,05\;\text{m}}{0,3 \;\frac{\text{m}}{\text{s}}} \\[5pt]
t&=& 3,5 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/23893e12b0d8ad7b8e384eaa95e0fe5263a76a27f014882370767a383bab917a_light.svg) Zeitpunkt zu dem die Welle das Ende des Bandes erreicht
Das Band ist
Zeitpunkt zu dem die Welle das Ende des Bandes erreicht
Das Band ist  lang. Somit folgt:
lang. Somit folgt:
 Nach
Nach  hat die Welle das rechte Ende des Bandes erreicht.
Reflexion der Welle
Am rechten Ende des Bandes wird die Welle nach links reflektiert. Da das rechte Ende des Bandes fest ist, kommt es zum Phasensprung. Die reflektierte und einlaufende Welle überlagern sich, wodurch sich eine stehende Welle bildet.
Zeitpunkt zu dem die reflektierte Welle den Ort
hat die Welle das rechte Ende des Bandes erreicht.
Reflexion der Welle
Am rechten Ende des Bandes wird die Welle nach links reflektiert. Da das rechte Ende des Bandes fest ist, kommt es zum Phasensprung. Die reflektierte und einlaufende Welle überlagern sich, wodurch sich eine stehende Welle bildet.
Zeitpunkt zu dem die reflektierte Welle den Ort  erreicht
Die reflektierte Welle erreicht den Ort
erreicht
Die reflektierte Welle erreicht den Ort  nachdem sie
nachdem sie  zurückgelegt hat.
zurückgelegt hat.

 Nach
Nach  erreicht die reflektierte Welle den Ort wieder, heißt nach
erreicht die reflektierte Welle den Ort wieder, heißt nach  schwingt das Band nicht mehr, da sich hier ein Knoten der schwingenden Welle befindet.
Zeit-Auslenkung-Diagramm
schwingt das Band nicht mehr, da sich hier ein Knoten der schwingenden Welle befindet.
Zeit-Auslenkung-Diagramm
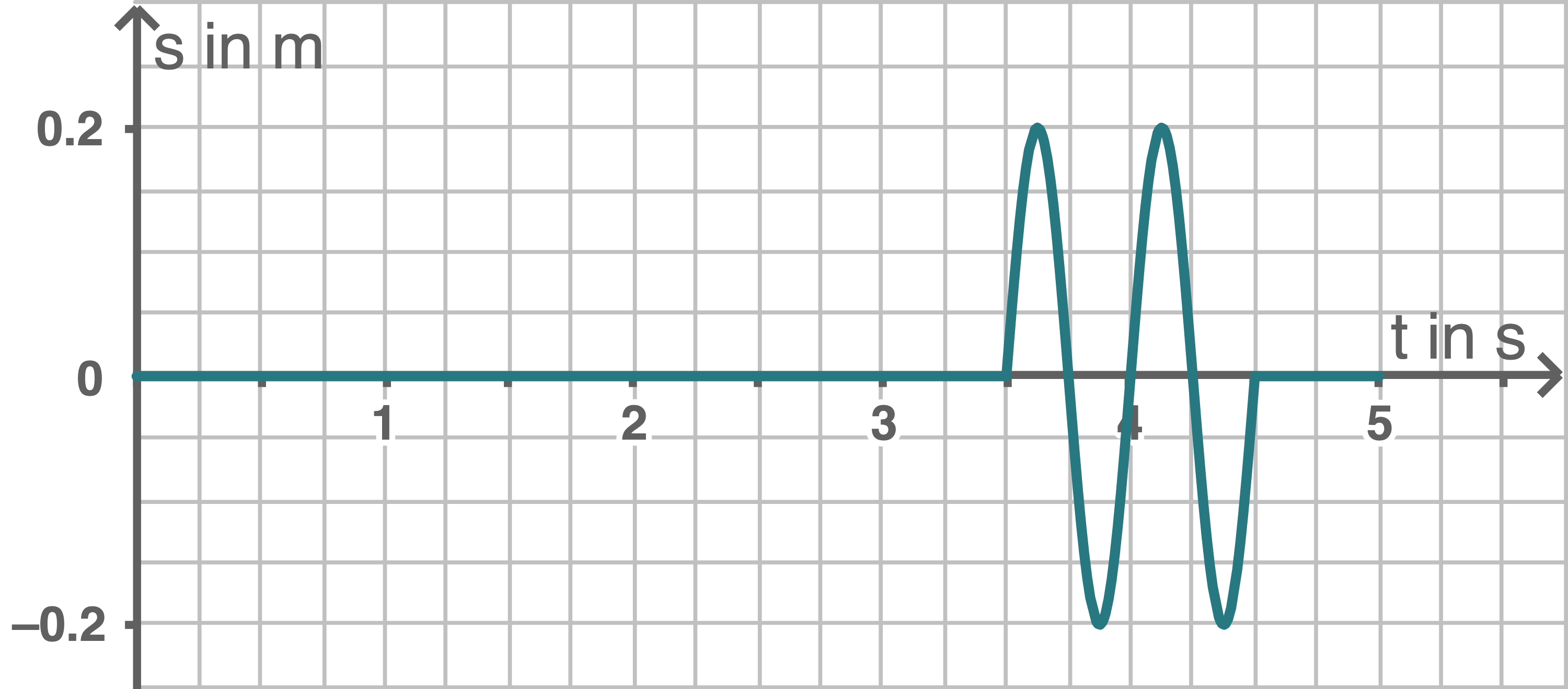

d)
Wenn die Beziehung  gilt, dann ist das Produkt
gilt, dann ist das Produkt  ungefähr konstant (im Rahmen der Messungenauigkeiten).
ungefähr konstant (im Rahmen der Messungenauigkeiten).
| 7,16 | 2 | 28,6 |
| 3,15 | 3 | 28,4 |
| 1,78 | 4 | 28,5 |
| 1,14 | 5 | 28,5 |
| 0,79 | 6 | 28,4 |
e)
Der Mittelwert ergibt  was dem Proportionalitätsfaktor entspricht.
was dem Proportionalitätsfaktor entspricht.
f)
3.
a)
Fällt Licht auf eine Kathode (z.B. Fotokathode), so überträgt es seine Energie auf die sich darin befindenden Elektronen. Die Energie der Lichtquanten beträgt  , dabei ist
, dabei ist  das Planck'sche Wirkungsquantum und
das Planck'sche Wirkungsquantum und  die Frequenz des Lichts.
Ist die die übertragene Energie der Lichtquanten groß genug, so können sich die Elektronen aus der Kathode lösen. Um sich aus der Kathode lösen zu können, benötigen die Elektronen auch Energie (die Ablöseenergie
die Frequenz des Lichts.
Ist die die übertragene Energie der Lichtquanten groß genug, so können sich die Elektronen aus der Kathode lösen. Um sich aus der Kathode lösen zu können, benötigen die Elektronen auch Energie (die Ablöseenergie  .) Die restliche Energie ist die kinetische Energie, mit der sich die Elektronen bewegen.
.) Die restliche Energie ist die kinetische Energie, mit der sich die Elektronen bewegen.
b)
Bei konstanter Lichtfrequenz variiert die Ablöseenergie  je nach Fotozelle und somit folglich auch die restliche kinetische Energie der Elektronen. Das beschreibt die Abbildung 4b am besten.
Da es keine negative kinetische Energie gibt, kommt Abb. 4a nicht in Frage.
je nach Fotozelle und somit folglich auch die restliche kinetische Energie der Elektronen. Das beschreibt die Abbildung 4b am besten.
Da es keine negative kinetische Energie gibt, kommt Abb. 4a nicht in Frage.
Da die kinetische Energie mit zunehmender Ablöseenergie linear abnimmt, kann auch Abb. 4c ausgeschlossen werden.
Da die kinetische Energie mit zunehmender Ablöseenergie linear abnimmt, kann auch Abb. 4c ausgeschlossen werden.
c)
Der  Zusammenhang kann mit verschiedenen Fotozellen konstanten Lichtes überprüft werden. Die verschiedenen Fotozellen, haben unterschiedliche, bekannte Ablöseenergie
Zusammenhang kann mit verschiedenen Fotozellen konstanten Lichtes überprüft werden. Die verschiedenen Fotozellen, haben unterschiedliche, bekannte Ablöseenergie  Licht mit einer konstanten Frequenz, was bei den Fotozellen die Spannung
Licht mit einer konstanten Frequenz, was bei den Fotozellen die Spannung  bestimmt. Mit der Spannung kann dann die maximale kinetische Energie
bestimmt. Mit der Spannung kann dann die maximale kinetische Energie  bestimmt werden und damit dann ein
bestimmt werden und damit dann ein  Diagramm erstellt werden.
Diagramm erstellt werden.
d)
Beim Fotoeffekt gibt es eine Grenzfrequenz, unterhalb der keine Elektronen mehr aus der Kathode gelöst werden können.
Beim klassischen Wellenmodell muss bei genügend hoher Intensität der Welle bei jeder Frequenz die Elektronenablösung möglich sein. Deshalb ist dieser Aspekt des Fotoeffekts nicht mit der klassischen Vorstellung von elektromagnetischen Wellen zu vereinen.
Beim klassischen Wellenmodell muss bei genügend hoher Intensität der Welle bei jeder Frequenz die Elektronenablösung möglich sein. Deshalb ist dieser Aspekt des Fotoeffekts nicht mit der klassischen Vorstellung von elektromagnetischen Wellen zu vereinen.