Aufgabe 1 – Mechanische Schwingungen
1.
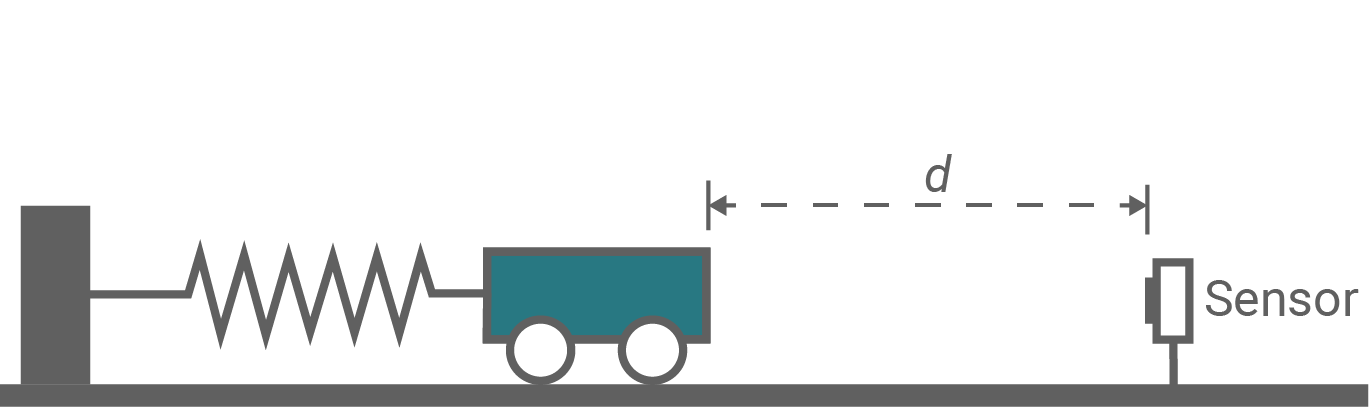
Ein Wagen mit der Masse  ist an einer auf Zug und Druck belastbaren Schraubenfeder mit der Federkonstanten
ist an einer auf Zug und Druck belastbaren Schraubenfeder mit der Federkonstanten  befestigt. Rechts neben dem Wagen befindet sich ein UItraschallsensor, der den Abstand
befestigt. Rechts neben dem Wagen befindet sich ein UItraschallsensor, der den Abstand  zur Seitenfläche des Wagens bestimmt (siehe Abb. 1).
zur Seitenfläche des Wagens bestimmt (siehe Abb. 1).
 und der Beschleunigung
und der Beschleunigung  des Wagens während einer Periode berechnen und darstellen. Dieser Zusammenhang ist in einem der drei Diagramme in Abbildung 3 dargestellt.
des Wagens während einer Periode berechnen und darstellen. Dieser Zusammenhang ist in einem der drei Diagramme in Abbildung 3 dargestellt.
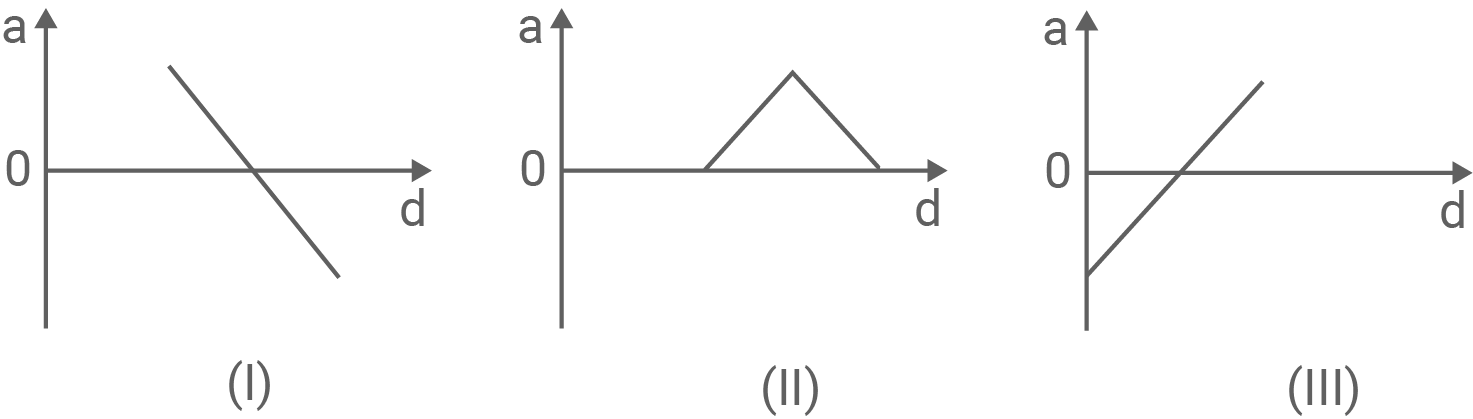

Abbildung 1
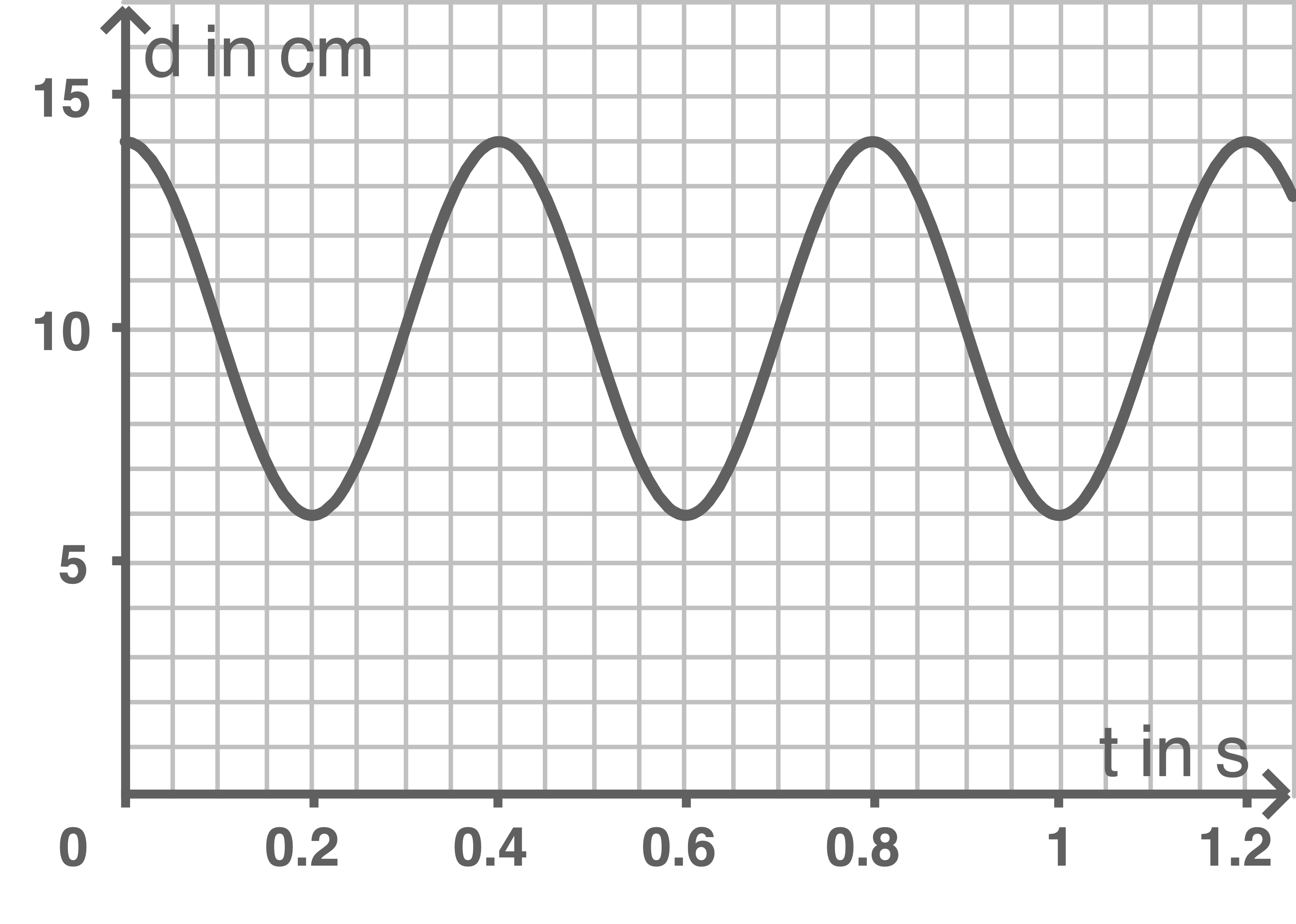
Von der Masse der Feder und Räder sowie von Reibungseinflüssen wird abgesehen. Der Wagen wird aus der Ruhelage nach links ausgelenkt und zum Zeitpunkt  freigegeben. Es entsteht eine harmonische Schwingung. Das vom Sensor aufgenommene Messdiagramm ist in Abbildung 2 dargestellt.
freigegeben. Es entsteht eine harmonische Schwingung. Das vom Sensor aufgenommene Messdiagramm ist in Abbildung 2 dargestellt.

Abbildung 2
a)
Bestimme die Amplitude und die Frequenz der Schwingung.
b)
Zeige, dass der Wagen eine Masse von  besitzt.
besitzt.
c)
Ermittle den Betrag der maximalen Geschwindigkeit des Wagens.
d)
Bestimme die kinetische Energie des Wagens zum Zeitpunkt  .
.
e)
Skizziere ein Zeit - kinetische Energie - Diagramm für die Schwingung im Bereich 
Die verwendete Messsoftware des Ultraschallsensors kann den Zusammenhang zwischen dem Abstand 
Abbildung 3
f)
Beurteile, welches der drei Diagramme den Zusammenhang korrekt darstellt.
(10 VP)
2.
Das linke Ende eines  langen linearen Wellenträgers beginnt zum Zeitpunkt
langen linearen Wellenträgers beginnt zum Zeitpunkt  mit der Frequenz
mit der Frequenz  aus der Gleichgewichtslage nach oben harmonisch zu schwingen. Es breitet sich eine nach rechts laufende Querwelle auf dem Wellenträger aus.
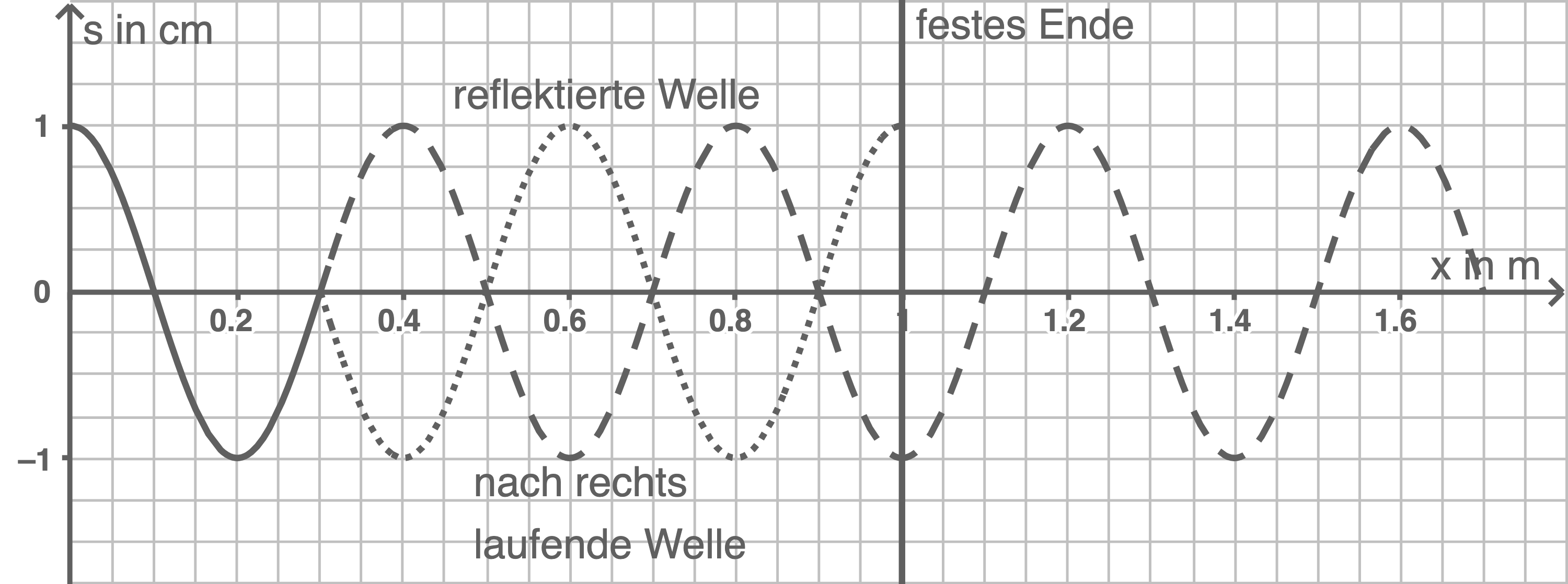
Abbildung 4 zeigt ein Momentanbild des Wellenträgers, nachdem bereits genau eine Reflexion stattgefunden hat.
aus der Gleichgewichtslage nach oben harmonisch zu schwingen. Es breitet sich eine nach rechts laufende Querwelle auf dem Wellenträger aus.
Abbildung 4 zeigt ein Momentanbild des Wellenträgers, nachdem bereits genau eine Reflexion stattgefunden hat.
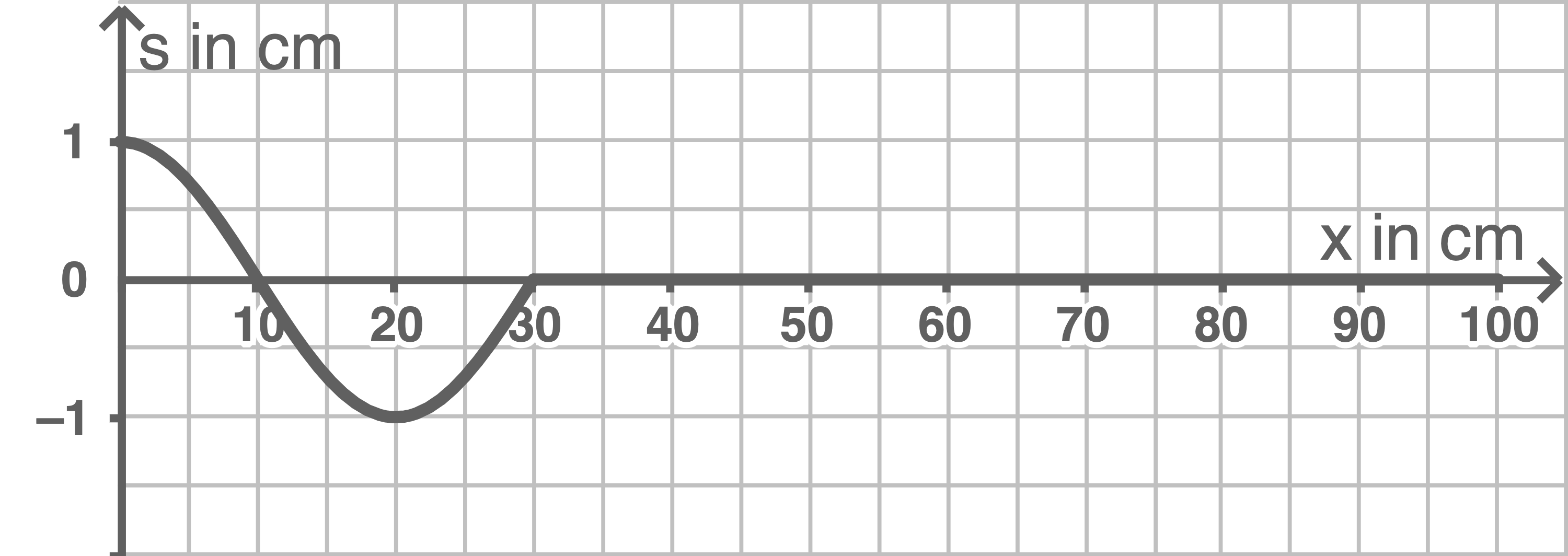

Abbildung 4
a)
Zeige, dass die Ausbreitungsgeschwindigkeit der Welle  beträgt.
beträgt.
b)
Bestimme den Zeitpunkt des Momentanbilds.
c)
Erläutere, dass sich bei  ein festes Ende befinden muss.
ein festes Ende befinden muss.
d)
Zeichne ein Zeit - Auslenkung - Diagramm für den Punkt an der Stelle  im Zeitintervall
im Zeitintervall  .
.
(9 VP)
3.
Zwei Stifte  und
und  , die in ein Wasserbecken eintauchen, haben einen Abstand von
, die in ein Wasserbecken eintauchen, haben einen Abstand von  Sie schwingen gleichphasig, harmonisch und mit gleicher Amplitude.
Sie schwingen gleichphasig, harmonisch und mit gleicher Amplitude.
Die erzeugten Wellen bewegen sich mit der Geschwindigkeit auf der Wasseroberfläche. Von einer Abnahme der Amplitude wird abgesehen.
auf der Wasseroberfläche. Von einer Abnahme der Amplitude wird abgesehen.
Abbildung 5 zeigt eine Momentaufnahme der Wasseroberfläche zu einem bestimmten Zeitpunkt nach Beginn der Schwingungen.
Die erzeugten Wellen bewegen sich mit der Geschwindigkeit
Abbildung 5 zeigt eine Momentaufnahme der Wasseroberfläche zu einem bestimmten Zeitpunkt nach Beginn der Schwingungen.

Abbildung 5
a)
Erkläre das Zustandekommen dieser dauerhaft in Ruhe befindlichen Bereiche.
Die Wasseroberfläche an der Stelle
b)
Zeige unter Verwendung dieser Angaben, dass die Wellenlänge  beträgt.
beträgt.
c)
Berechne die Frequenz der beiden Stifte.
Von einer Schülerin wird über die Wasserbewegung auf der Strecke zwischen den Erregern „Zum Zeitpunkt der Aufnahme befinden sich alle Teilchen zwischen
d)
Beurteile diese Aussage.
Die Frequenz der Stifte wird nun langsam erhöht, so dass sich die Bereiche, die dauerhaft in Ruhe bleiben, in der Wanne sichtbar verschieben. Die Ausbreitungsgeschwindigkeit der Wellen ändert sich dabei nicht.
e)
Ermittle, auf welchen Wert die Frequenz mindestens vergrößert werden muss, damit die Stelle  erneut in einem Bereich liegt, der dauerhaft in Ruhe ist.
erneut in einem Bereich liegt, der dauerhaft in Ruhe ist.
f)
Bestimme den Frequenzbereich, für den sich in der Wanne auf Dauer keine Bereiche mit unbewegter Wasseroberfläche mehr ausbilden können.
(11 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Aus Abbildung 2 wird eine Amplitude von  und eine Schwingungsdauer von
und eine Schwingungsdauer von  abgelesen.
Die Frequenz wird wie folgt berechnet:
abgelesen.
Die Frequenz wird wie folgt berechnet:
![\(\begin{array}[t]{rll}
f&=& \dfrac{1}{T} \\[5pt]
f&=& \dfrac{1}{0,4 \; \mathrm{s}} \\[5pt]
f&=& 2,5 \; \mathrm{Hz}
\end{array}\)](https://www.schullv.de/resources/formulas/e28b08a832f9b5c0516af0b31df26970fcb7c9ff7150a164b7bd502aadd1914a_light.svg)
b)
Gegeben: 
 Gesucht:
Gesucht:  Lösung: Die Schwingungsdauer einer harmonischen Schwingung beträgt
Lösung: Die Schwingungsdauer einer harmonischen Schwingung beträgt  1. Schritt: Auflösen nach
1. Schritt: Auflösen nach 
![\(\begin{array}[t]{rll}
T &=& 2 \pi \cdot \sqrt{\dfrac{m}{D}} \quad \scriptsize \mid\; (\;)^2 \\[5pt]
T^2 &=& 4\pi^2 \cdot \dfrac{m}{D} \quad \scriptsize \mid\; \cdot D \mid \; :4\pi^2 \\[5pt]
\dfrac{T^2 \cdot D}{4\pi^2} &=& m \\[5pt]
m &=& \dfrac{T^2 \cdot D}{4\pi^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7417014b994625a1cad0816fc009c4d7c66c257ca2f5acbfec8fcf8bc5c1bc16_light.svg) 2. Schritt: Einsetzen der Werte
2. Schritt: Einsetzen der Werte
![\(\begin{array}[t]{rll}
m &=& \dfrac{(0,40 \mathrm{~s})^{2}}{4 \pi^{2}} \cdot 74,0 \,\frac{\mathrm{N}}{\text{m}} \\[5pt]
m &=& 300 \; \mathrm{g}
\end{array}\)](https://www.schullv.de/resources/formulas/f0aba5d309503deaefd4a93536f3fe0bfa5257d1f9d7bc6860a1ef862f0e7fc4_light.svg)
c)
1. Schritt: Herleitung
Der Abstand des Wagens zum Sensor wird durch folgende Funktion beschrieben:
 Dabei entspricht
Dabei entspricht  und
und  (Abzulesen aus Abbildung 2)
Die Geschwindigkeit ergibt sich aus der ersten Ableitung:
(Abzulesen aus Abbildung 2)
Die Geschwindigkeit ergibt sich aus der ersten Ableitung:
 2. Schritt: Betrag der maximalen Geschwindigkeit des Körpers ermitteln
2. Schritt: Betrag der maximalen Geschwindigkeit des Körpers ermitteln
![\(\begin{array}[t]{rll}
v_{\max } &=& s_{\max } \cdot \omega \\[5pt]
v_{\max } &=& s_{\max } \cdot 2 \pi \cdot f
\end{array}\)](https://www.schullv.de/resources/formulas/7f2aa463a3cb78ca23041fed9cfe73b04028806ec44075f7b59eb9aaa54e38ae_light.svg) Einsetzen der Werte:
Einsetzen der Werte:
![\(\begin{array}[t]{rll}
v_{\max } &=& 0,04 \mathrm{~m} \cdot 2 \pi \cdot 2,5 \mathrm{~Hz} \\[5pt]
v_{\max } &=& 0,63 \;\frac{\mathrm{m}}{\mathrm{s}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d62feed528a89b26e17d9e797bab073f6479981fa30176e5bee4d5f54f027d3a_light.svg)
d)
Aus Abbildung 2: Zum Zeitpunkt  schwingt der Körper durch die Gleichgewichtslage und erreicht damit seine maximale Geschwindigkeit
schwingt der Körper durch die Gleichgewichtslage und erreicht damit seine maximale Geschwindigkeit  Gegeben:
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
E_{\text{kin}} &=& \dfrac{1}{2} \cdot m \cdot v_{\max }^{2} \\[5pt]
E_{\text{kin}} &=& \dfrac{1}{2} \cdot 0,3 \mathrm{~kg} \cdot\left(0,63 \; \frac{\text{m}}{\text{s}} \right)^{2} \\[5pt]
E_{\text{kin}} &=& 0,059 \mathrm{J}
\end{array}\)](https://www.schullv.de/resources/formulas/1765f2a8e2009a97997bf348a81cf5b71275992aa914b79c6ead36b2dfeac67c_light.svg)
e)
Die maximale kinetische Energie besitzt der Wagen, wenn er durch die Gleichgewichtslage schwingt. Dies passiert zu den Zeitenpunkten  und
und 
Die kinetische Energie ist null, wenn der Wagen maximal ausgelenkt ist. Dies passiert zu den Zeitpunkten sowie
sowie 
Folglich ist der Verlauf der kinetischen Energie periodisch und kann mit einer Sinus-Funktion modelliert werden.
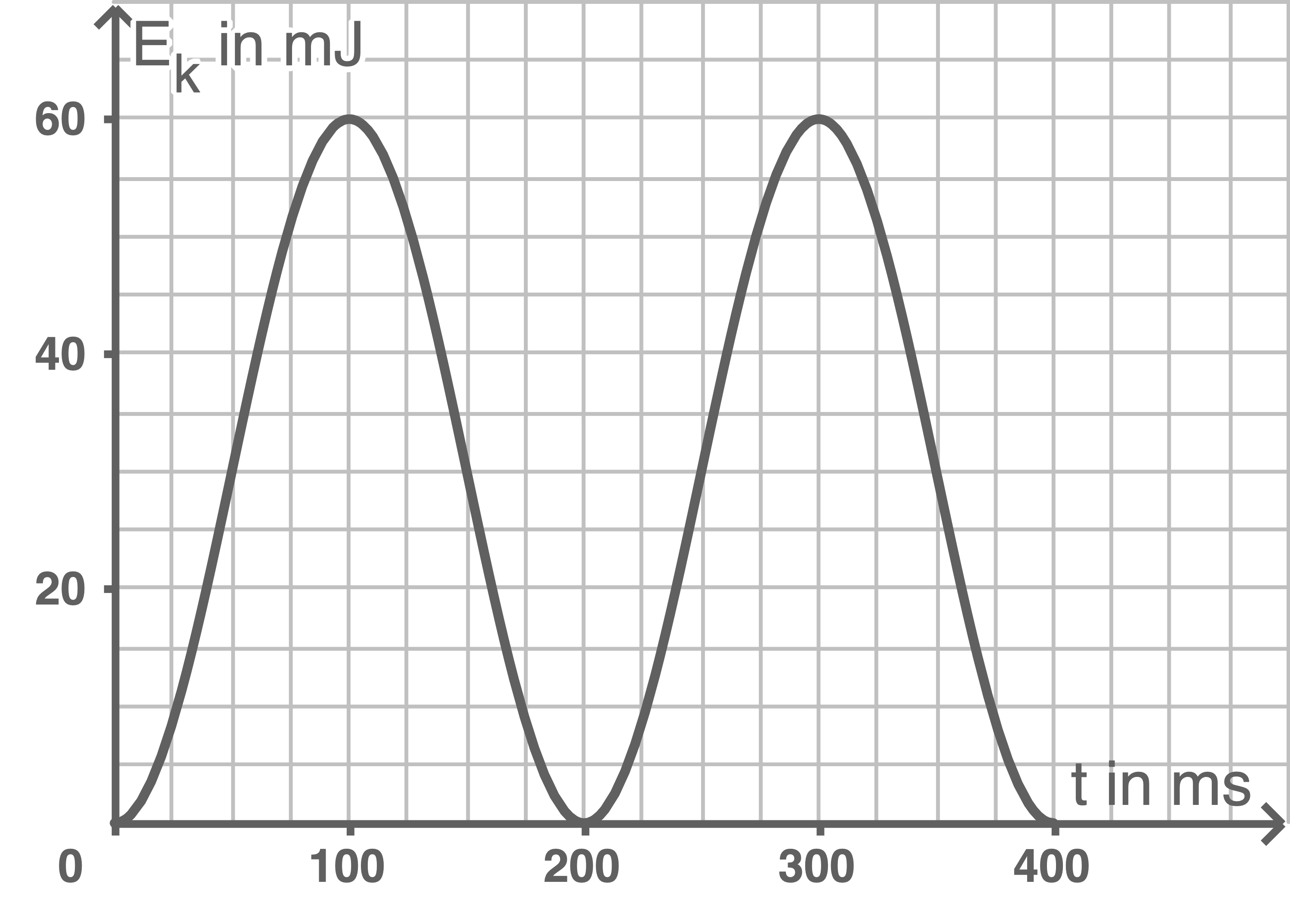
Die kinetische Energie ist null, wenn der Wagen maximal ausgelenkt ist. Dies passiert zu den Zeitpunkten
Folglich ist der Verlauf der kinetischen Energie periodisch und kann mit einer Sinus-Funktion modelliert werden.

f)
Bei diesem harmonischen Oszillator besteht ein linearer Zusammenhang zwischen momentaner Beschleunigung und Abstand zum Sensor, es treten zudem positive und negative Beschleunigungswerte auf.
Dies ist in Diagramm (i) korrekt dargestellt. Diagramm (ii) kommt nicht in Frage, da es nur positive Beschleunigungswerte zeigt. Diagramm (iii) kommt ebenfalls nicht in Frage, da bei der vorliegenden Schwingung der Abstand zum Sensor nicht Null wird.
Dies ist in Diagramm (i) korrekt dargestellt. Diagramm (ii) kommt nicht in Frage, da es nur positive Beschleunigungswerte zeigt. Diagramm (iii) kommt ebenfalls nicht in Frage, da bei der vorliegenden Schwingung der Abstand zum Sensor nicht Null wird.
2
a)
Gegeben:  Aus Abbildung 4 ergibt sich für die Wellenlänge der Wert
Aus Abbildung 4 ergibt sich für die Wellenlänge der Wert  also
also  Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
c &=& \lambda \cdot f \\[5pt]
c &=& 0,4 \mathrm{~m} \cdot 0,4 \mathrm{~Hz} \\[5pt]
c &=& 0,16 \; \dfrac{\text{m}}{\text{s}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a91441205ab2eb2ed72c95314b70e5cb4a4270b730f7cc5680083783e425e154_light.svg)
b)
Die Welle bewegt sich zuerst einen Meter nach rechts. Dort wird sie reflektiert und bewegt sich 0,7 Meter nach links. Sie hat bis sie sich mit der nach rechts laufenden Welle überlagert den Weg  zurückgelegt, das sind
zurückgelegt, das sind  Wellenlängen.
Wellenlängen.
Man erhält als Zeit:![\(\begin{array}[t]{rll}
t &=& \dfrac{\Delta x}{c} \\[5pt]
t &=& \dfrac{1,7 \mathrm{~m}}{0,16 \mathrm{~ms}^{-1}} \\[5pt]
t &=& 10,625 \mathrm{~s}
\end{array}\)](https://www.schullv.de/resources/formulas/68163826196b49441739599e73827082079490dc602bfb304956d1ce105e4c15_light.svg)
Man erhält als Zeit:
c)
In Abbildung 4 befinden sich zum Aufnahmezeitpunkt alle Oszillatoren im Bereich  in ihrer Gleichgewichtslage. Die Auslenkungen dieser Oszillatoren in der reflektierten bzw. in der nach rechts laufenden Welle addieren sich demnach an jeder Stelle zu Null. Mithilfe der Konstruktion dieser stehenden Welle lässt sich erkennen, dass dies der Fall ist, wenn die Welle mit einem Phasensprung von
in ihrer Gleichgewichtslage. Die Auslenkungen dieser Oszillatoren in der reflektierten bzw. in der nach rechts laufenden Welle addieren sich demnach an jeder Stelle zu Null. Mithilfe der Konstruktion dieser stehenden Welle lässt sich erkennen, dass dies der Fall ist, wenn die Welle mit einem Phasensprung von  reflektiert wird. Bei
reflektiert wird. Bei  liegt ein festes Ende des Wellenträgers vor.
liegt ein festes Ende des Wellenträgers vor.

d)
Die Stelle  wird von der Welle nach erreicht nach:
wird von der Welle nach erreicht nach:
![\(\begin{array}[t]{rll}
\Delta t_{1}&=& \dfrac{\Delta x}{c} \\[5pt]
\Delta t_{1}&=& \dfrac{0,6 \mathrm{~m}}{0,16 \mathrm{~ms}^{-1}} \\[5pt]
\Delta t_{1}&=& 3,75 \mathrm{~s}\\[5pt]
\Delta t_{1}&=& 1,5 \; \mathrm{T}
\end{array}\)](https://www.schullv.de/resources/formulas/a65fd68036b3e9aeee8c170bd4d126c9160164c855ccfcf7fa348a802bbc62e4_light.svg) Hier beginnt der Oszillator mit seiner Schwingung nach oben und mit einer Amplitude von
Hier beginnt der Oszillator mit seiner Schwingung nach oben und mit einer Amplitude von  Die reflektierte Welle wird erreicht nach:
Die reflektierte Welle wird erreicht nach:
![\(\begin{array}[t]{rll}
\Delta t_{2}&=& \dfrac{\Delta x}{c} \\[5pt]
\Delta t_{2}&=& \dfrac{0,8 \mathrm{~m}}{0,16 \mathrm{~ms}^{-1}} \\[5pt]
\Delta t_{2}&=& 5 \mathrm{~s}\\[5pt]
\Delta t_{2}&=& 2 \; \mathrm{T}
\end{array}\)](https://www.schullv.de/resources/formulas/10cdf029313687650243cf61642183b0e5494dd51d49507e6a5038d8b4a11c1b_light.svg) Ab diesem Zeitpunkt befindet sich der Oszillator in Ruhe, da er vom festen Ende des Wellenträgers den Abstand
Ab diesem Zeitpunkt befindet sich der Oszillator in Ruhe, da er vom festen Ende des Wellenträgers den Abstand  hat. Er befindet sich in einem Schwingungsknoten der stehenden Welle.
hat. Er befindet sich in einem Schwingungsknoten der stehenden Welle.
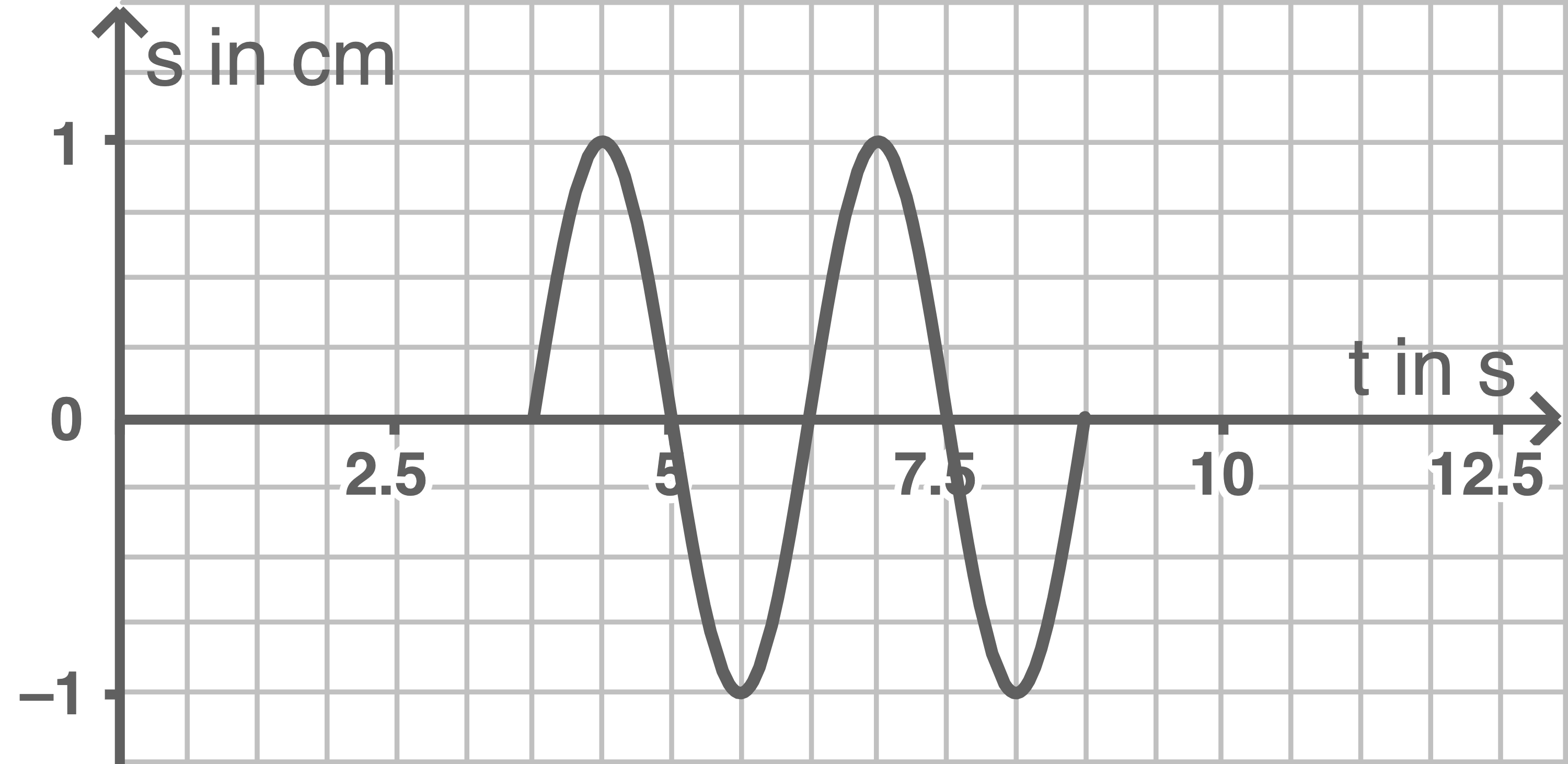

3
a)
In der Wellenwanne interferieren die von  bzw.
bzw.  ausgehenden Wellen mit einem gewissen Gangunterschied. Ist der Gangunterschiede ein ungeradzahliges Vielfaches der halben Wellenlänge, so löschen sich an diesen Stellen die beiden Wellen aus. Die Wasseroberfläche bleibt hier dauerhaft in Ruhe.
ausgehenden Wellen mit einem gewissen Gangunterschied. Ist der Gangunterschiede ein ungeradzahliges Vielfaches der halben Wellenlänge, so löschen sich an diesen Stellen die beiden Wellen aus. Die Wasseroberfläche bleibt hier dauerhaft in Ruhe.
b)
c)
d)
Zwischen  bzw.
bzw.  interferieren gegenläufige Wellen, es bildet sich dort eine stehende Welle aus. Bei einer stehenden Welle sind die Oszillatoren nur dann momentan in Ruhe, wenn sie Ihre maximale Auslenkung erreicht haben. Dies ist hier sicher nicht der Fall, da der Bereich zwischen
interferieren gegenläufige Wellen, es bildet sich dort eine stehende Welle aus. Bei einer stehenden Welle sind die Oszillatoren nur dann momentan in Ruhe, wenn sie Ihre maximale Auslenkung erreicht haben. Dies ist hier sicher nicht der Fall, da der Bereich zwischen  und
und  in der Aufnahme weder schwarze noch weiße Zonen erkennen lässt. Aus diesem Grund ist die Aussage der Schülerin falsch.
in der Aufnahme weder schwarze noch weiße Zonen erkennen lässt. Aus diesem Grund ist die Aussage der Schülerin falsch.
e)
Bei größer werdender Frequenz wird die Wellenlänge kleiner. In P findet erneut destruktive Interferenz statt, wenn dort für den Gangunterschied gilt:
![\(\begin{array}[t]{rll}
\Delta s &=& \dfrac{3}{2} \cdot \lambda \\[5pt]
\Delta s &=& \dfrac{3}{2} \cdot \dfrac{c}{f} &\quad \scriptsize \mid\; \cdot \dfrac{f}{\Delta s} \\[5pt]
f &=& \dfrac{3}{2} \cdot \dfrac{c}{\Delta s} \\[5pt]
f &=& \dfrac{3}{2} \cdot \dfrac{20 \; \mathrm{cms}^{-1}}{0,5 \mathrm{~cm}} \\[5pt]
f &=& 60 \mathrm{~Hz}
\end{array}\)](https://www.schullv.de/resources/formulas/b4b0d9ddd38fdce598ce2de09c9252b1b2294c0becb2d90cfbcae46572234aea_light.svg) Somit beträgt die nächstgrößere Frequenz
Somit beträgt die nächstgrößere Frequenz 
f)
Die beiden Wellenerreger haben einen Abstand von  . Das ist der maximal mögliche Gangunterschied in der Wellenwanne.
Für
. Das ist der maximal mögliche Gangunterschied in der Wellenwanne.
Für  löschen sich die Wellen längs der Geraden durch
löschen sich die Wellen längs der Geraden durch  bzw.
bzw.  links von
links von  bzw. rechts von
bzw. rechts von  aus. Die dazu passende Frequenz beträgt:
aus. Die dazu passende Frequenz beträgt:
![\(\begin{array}[t]{rll}
f&=& \dfrac{c}{\lambda} \\[5pt]
f&=& \dfrac{20 \mathrm{~cms}^{-1}}{6 \mathrm{~cm}} \\[5pt]
f&=& \dfrac{10}{3} \mathrm{~Hz} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/24e1a60e17c5c74f7f4fb793f0d00b24909937ec2cbe80c917965632bf4abce5_light.svg) Für
Für  gibt es in der Wellenwanne keine Punkte, die dauerhaft in Ruhe sind.
gibt es in der Wellenwanne keine Punkte, die dauerhaft in Ruhe sind.