Aufgabe 2 — Abschirmung gegen Meereswellen

Ins Meer ragende künstliche Aufschüttungen, sogenannte Molen, sollen dafür sorgen, dass dahinter liegende Hafenbecken möglichst gut vor Meereswellen geschützt werden.

Bei der Planung von Hafenbecken können die dort auftretenden Wellenphänomene wie beispielsweise Interferenz im Modell in kleinen Wellenwannen wie in Material 1 untersucht werden.

Nenne zwei weitere Wellenphänomene, die mithilfe eines solchen Versuchsaufbaus beobachtet werden könnten.

2 BE

Erkläre, wie es in der Wellenwanne zu dem in Material 1 beobachteten rautenförmigen Muster kommt.

3 BE

Nun wird in Material 2 eine vom Meer einlaufende ebene Wellenfront betrachtet, die annähernd parallel zur Mole verläuft.

Begründe mit einer geeigneten Modellierung, dass sich hinter der Mole Wellen ausbreiten.

3 BE

Zur Erhebung von meteorologischen und ozeanographischen Daten werden sowohl in Häfen als auch im freien Meer an der Wasseroberfläche schwimmende Bojen eingesetzt (siehe Material 3). Eine solche Boje wird hier als vertikal harmonisch schwingendes System modelliert.

Gib allgemein an, unter welcher Bedingung es zu einer harmonischen Schwingung kommt.

2 BE

Zeige anhand der in Material 4 angegebenen Differenzialgleichung, dass sich mit dem Ansatz $Formula: s(t)=\hat{s} \cdot \sin (\omega \cdot t)$ $Formula: s(t)=\hat{s} \cdot \sin (\omega \cdot t)$ für die Periodendauer Formula: T der Schwingung der Boje folgende Gleichung ergibt:

$Formula: T = 2 \pi \cdot \sqrt{\frac{m}{A \cdot \rho \cdot g}}.$ $Formula: T = 2 \pi \cdot \sqrt{\frac{m}{A \cdot \rho \cdot g}}.$

8 BE

Berechne die Frequenz der freien Schwingung der Boje aus Material 3. Gehe von einer Dichte des Wassers von $Formula: \mathrm{\rho}=1,0 \; \frac{\mathrm{g}}{\mathrm{cm}^3}$ $Formula: \mathrm{\rho}=1,0 \; \frac{\mathrm{g}}{\mathrm{cm}^3}$ aus.

6 BE

Die Boje kann von Wasserwellen zu vertikalen erzwungenen Schwingungen angeregt werden.

Beschreibe anhand von Material 5, welchen Einfluss die Erregerfrequenz Formula: f_e auf die Amplitude einer erzwungenen Schwingung hat.

3 BE

Begründe, dass die Wellen aus Material 6 in der Lage wären, die betrachtete Boje stark in Schwingung zu versetzen.

4 BE

Um starke Schwingungen der Boje zu vermeiden, wird vorgeschlagen, ihre Masse und ihre Querschnittsfläche zu verändern.

Diskutiere diesen Vorschlag im Rahmen der Modellierung aus den Aufgaben 3 und 4.

5 BE

In Material 7 werden verschiedene Informationen zur Bauweise von Molen gegeben und dargestellt, wie eine Schwimmmole im Vergleich zu einer geschlossenen Mole gebaut ist.

Bewerte die beiden Molentypen hinsichtlich ihrer Eignung in den folgenden Situationen:

$Formula: \mathrm{I})$ $Formula: \mathrm{I})$	Ein Hafenbecken soll so stark wie möglich von Wellen beruhigt werden.
$Formula: \mathrm{II})$ $Formula: \mathrm{II})$	Der Hafen soll in der Nähe eines Wasserschutzgebietes gebaut werden, wobei das Ökosystem unter Wasser möglichst wenig beeinträchtigt werden soll.

4 BE

Material 1: Wellenwanne

Wasseroberfläche mit regelmäßigen Wellenmustern und zwei länglichen Messbalken

Abb. 1: Modell eines Hafenbeckens in der Wellenwanne. Die Wellen laufen von links unten ein.

Quelle: Liebs, Wilhelm (1964): Die Abschirmung von Seehäfen gegen Seegang.

In: Mitteilungsblatt der Bundesanstalt für Wasserbau 21. Karlsruhe: Bundesanstalt für Wasserbau. S. 45-70. CC BY

Material 2: Mole

Abb. 2: Mole in Rostock

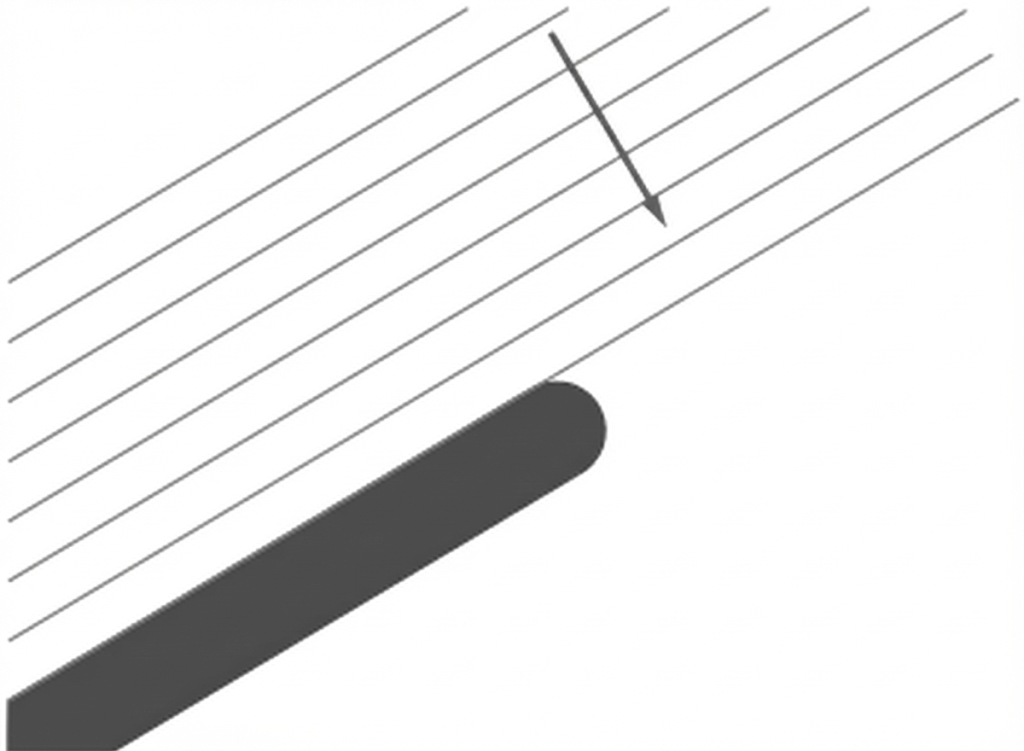
Diagonale parallele Linien mit Pfeil nach unten und dickem, abgerundetem Balken

Abb. 3: Vereinfachtes Modell der Mole und des Wellenverlaufs vor der Mole

Material 3: Boje

Durchmesser in Metern
Form	zylindrisch
Masse in Kilogramm

Abb. 4: Boje

Material 4: Differenzialgleichung

Wird eine solche Boje bezüglich der Wasseroberfläche vertikal ausgelenkt, dann kann die Bewegung der Boje idealisiert mit der folgenden Differenzialgleichung beschrieben werden:

$Formula: m \cdot \ddot{s}(t) + A \cdot \rho \cdot g \cdot s(t) = 0.$ $Formula: m \cdot \ddot{s}(t) + A \cdot \rho \cdot g \cdot s(t) = 0.$

Dabei ist Formula: s die vertikale Auslenkung aus der Ruhelage, Formula: m die Masse und Formula: A die Querschnittsfläche der Boje auf der Wasseroberfläche, $Formula: \rho$ $Formula: \rho$ die Dichte des Wassers und Formula: g die Erdbeschleunigung.

Material 5: Resonanzkurve

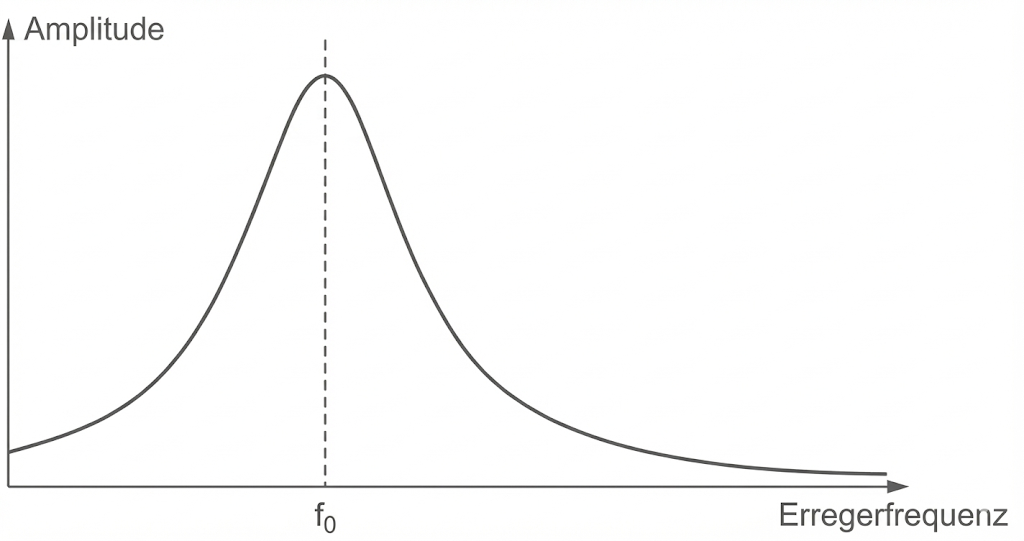
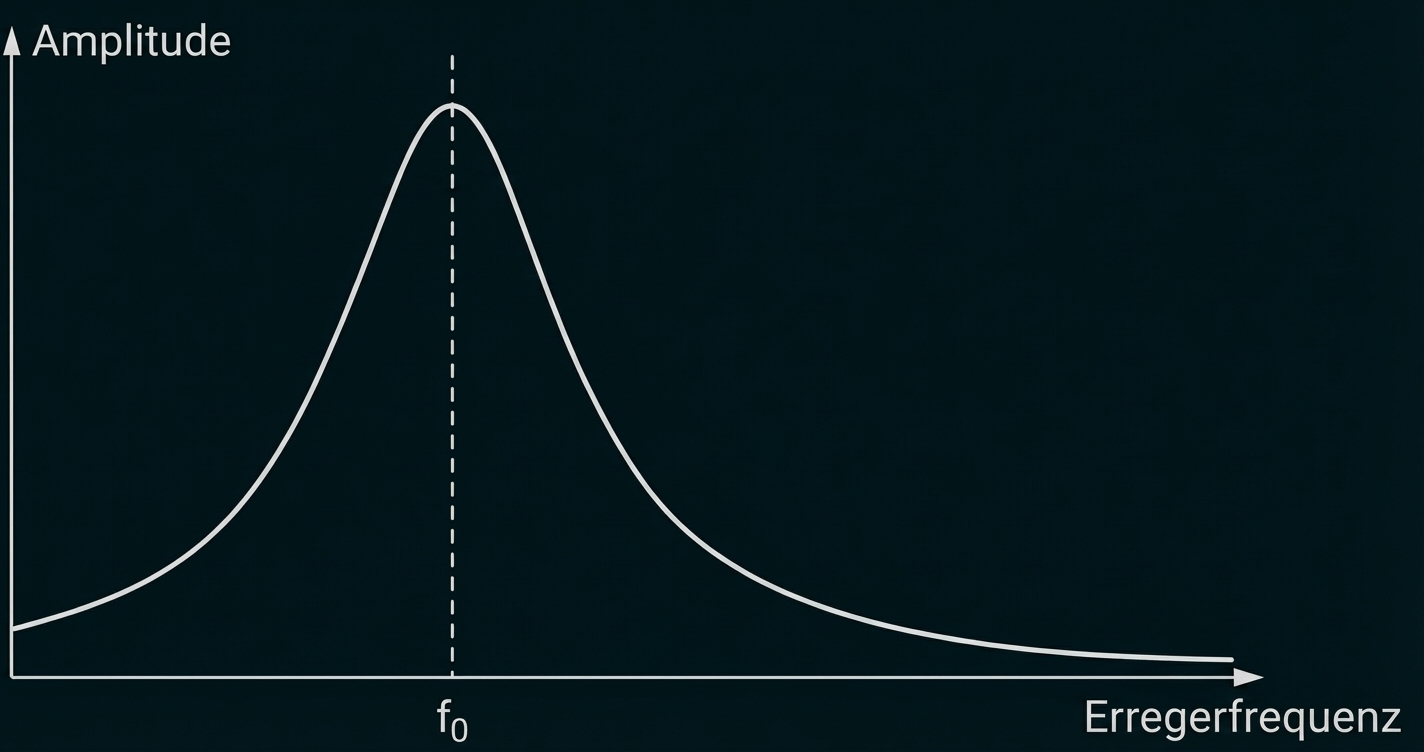
Einfaches Diagramm: Amplitude gegen Erregerfrequenz mit Peak bei f0.

Abb. 5: Resonanzkurve mit Eigenfrequenz $Formula: \mathrm{f}_0$ $Formula: \mathrm{f}_0$

Material 6: Wellengrößen

Mit dem Messsystem der Boje wurden folgende Werte für die Wasserwellen ermittelt:

Wellenlänge	$Formula: 12 \; \mathrm{m}$ $Formula: 12 \; \mathrm{m}$
Ausbreitungsgeschwindigkeit	$Formula: 22,0 \; \tfrac{\mathrm{km}}{\mathrm{h}}$ $Formula: 22,0 \; \tfrac{\mathrm{km}}{\mathrm{h}}$
Amplitude	$Formula: 20 \; \mathrm{cm}$ $Formula: 20 \; \mathrm{cm}$

Material 7: Bauweise verschiedener Molen

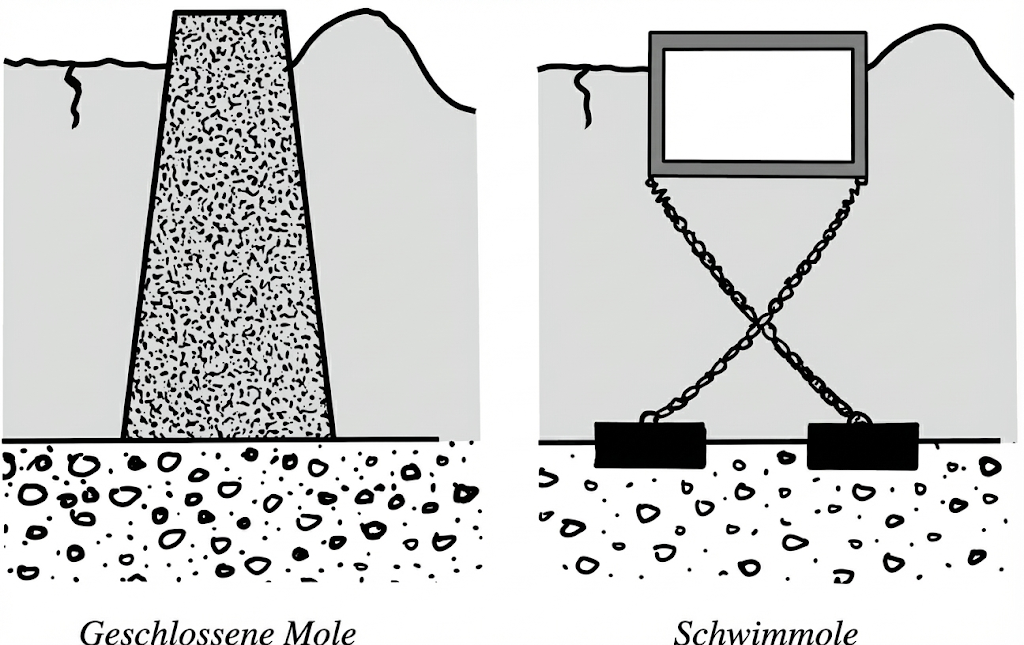
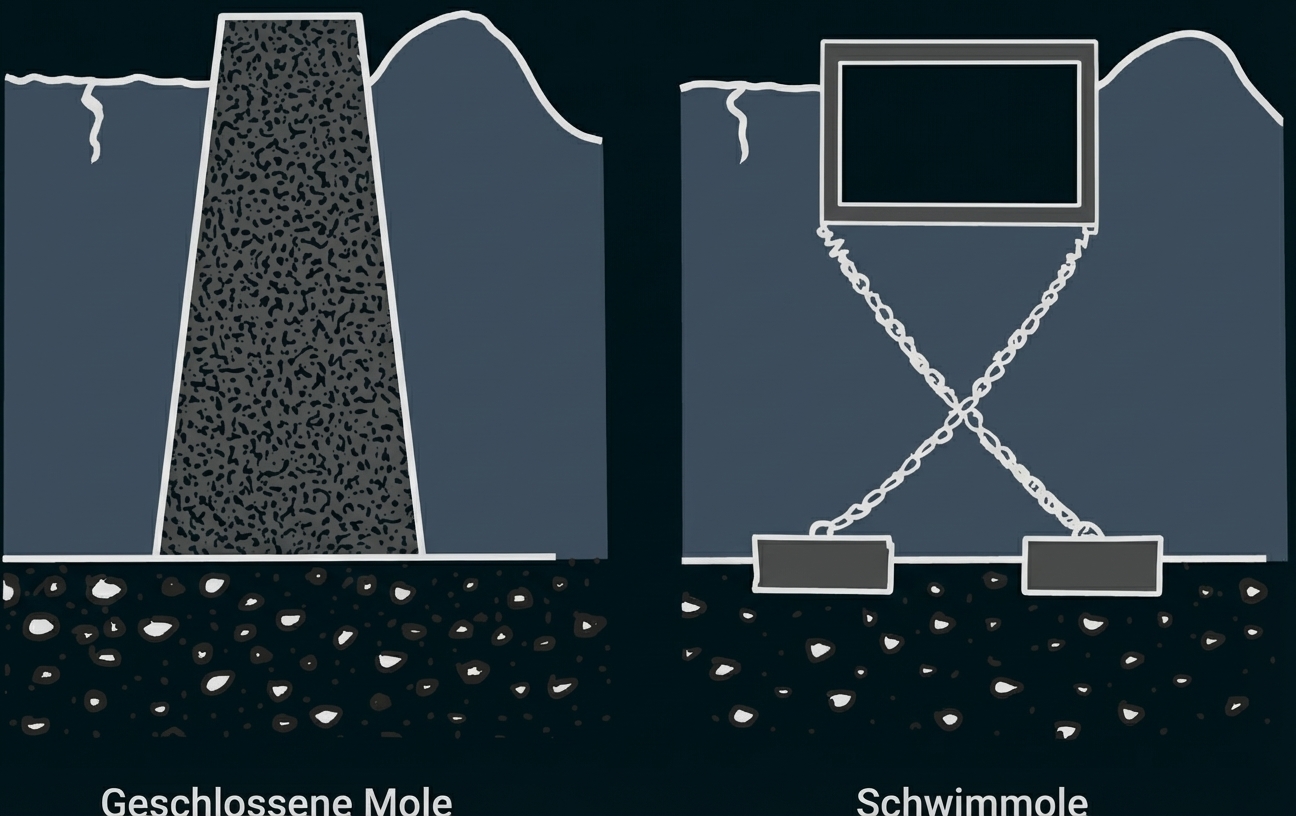
Zwei Skizzen: links geschlossene Mole, massives Erdwerk bis zum Meeresboden; rechts Schwimmole mit Schwimmkörper, gekreuzten Ketten und Grundankern.

Abb. 6: Bauweise verschiedener Molen im Querschnitt

„Wellendämpfung bei Schwimmolen: Der schwere, im Wasser liegende Schwimmkörper lässt die ankommenden Wellen an sich aufprallen und zum Teil reflektieren. Dabei wird jedoch ein Teil der Energiefortpflanzung weiterhin unter der Schwimmole durch stattfinden. Deshalb entstehen auch bei größeren Schwimmhafenanlagen Wellen im Hafeninneren. Die Höhen dieser Wellen sind bei einer gelungenen Konstruktion wesentlich geringer als die seeseitig aufprallenden Wellen.“

Quelle: F. Schaad: Zur Konstruktion von schwimmenden Hafenmolen

In: Schweizer Ingenieur und Architekt 98 (1980), S. 85f.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Reflexion, Beugung und Brechung.

Anmerkung: Es reicht zwei dieser Phänomene zu nennen.

Die parallel zueinander verlaufenden Wellenfronten bewegen sich von links unten auf ein gerades Hindernis zu, das etwa im $Formula: 45 ^\circ$ $Formula: 45 ^\circ$ Winkel zu den Wellenfronten steht. An diesem Hindernis werden die Wellen reflektiert und laufen anschließend nach rechts unten in neuen Wellenfronten weiter. Die reflektierten Wellen und die einlaufenden Wellen überlagern sich, wodurch ein Muster aus Rauten entsteht.

Gemäß dem Huygens'schen Prinzip kann jeder Punkt einer Wellenfront als Ursprung für eine neue, kreisförmige Elementarwelle betrachtet werden. Solange keine Hindernisse vorhanden sind, überlagern sich diese Elementarwellen zu einer linearen parallelen Wellenfront. Trifft die Wellenfront nun jedoch auf ein Hindernis wie der Mole, wird diese Wellenfront unterbrochen. Somit gelangen nun nur noch die kreisförmigen Elementarwellen hinter die Mole, wodurch sich die Wellen hinter der Mole kreisförmig ausbreiten.

Eine harmonische Bewegung tritt immer dann auf, wenn eine Rückstellkraft Formula: F proportional zu einer Auslenkung Formula: s ist und ihr entgegengesetzt wirkt.

Gegeben ist die Differenzialgleichung:

$Formula: \mathrm{(I)}$ $Formula: \mathrm{(I)}$ $Formula: m \cdot \ddot{s}(t) + A \cdot \rho \cdot g \cdot s(t) = 0,$ $Formula: m \cdot \ddot{s}(t) + A \cdot \rho \cdot g \cdot s(t) = 0,$

sowie der Lösungsansatz:

$Formula: \mathrm{(II)}$ $Formula: \mathrm{(II)}$ $Formula: s(t) = \hat{s} \cdot \sin(\omega \cdot t).$ $Formula: s(t) = \hat{s} \cdot \sin(\omega \cdot t).$

Durch zweimaliges Ableiten von $Formula: \mathrm{(II)}$ $Formula: \mathrm{(II)}$ und Einsetzen von $Formula: \mathrm{(II)}$ $Formula: \mathrm{(II)}$ in die zweite Ableitung ergibt sich:

$Formula: \begin{array}{rll}\ddot{s}(t) & = & -\omega^2 \cdot \hat{s} \cdot \sin(\omega \cdot t) \\[5pt]\ddot{s}(t) & = & -\omega^2 \cdot s(t)\end{array}$ $Formula: \begin{array}{rll}\ddot{s}(t) & = & -\omega^2 \cdot \hat{s} \cdot \sin(\omega \cdot t) \\[5pt]\ddot{s}(t) & = & -\omega^2 \cdot s(t)\end{array}$

Das lässt sich in $Formula: \mathrm{(I)}$ $Formula: \mathrm{(I)}$ einsetzen:

$Formula: \begin{array}{rll}m \cdot (-\omega^2 \cdot s(t)) + A \cdot \rho \cdot g \cdot s(t) & = & 0 \\[5pt](-\omega^2 \cdot m + A \cdot \rho \cdot g) \cdot s(t) & = & 0\end{array}$ $Formula: \begin{array}{rll}m \cdot (-\omega^2 \cdot s(t)) + A \cdot \rho \cdot g \cdot s(t) & = & 0 \\[5pt](-\omega^2 \cdot m + A \cdot \rho \cdot g) \cdot s(t) & = & 0\end{array}$

Diese Gleichung soll unabhängig von der Zeit Formula: t sein. Formula: s(t)=0 gilt jedoch nicht für alle , somit muss der Term in der Klammer bereits Formula: 0 sein:

$Formula: -\omega^2 \cdot m + A \cdot \rho \cdot g = 0$ $Formula: -\omega^2 \cdot m + A \cdot \rho \cdot g = 0$

$Formula: \Rightarrow \omega = \sqrt{\dfrac{A \cdot \rho \cdot g}{m}}.$ $Formula: \Rightarrow \omega = \sqrt{\dfrac{A \cdot \rho \cdot g}{m}}.$

Es gilt $Formula: T=\tfrac{2 \pi}{\omega}.$ $Formula: T=\tfrac{2 \pi}{\omega}.$ Daraus folgt für die Periodendauer Formula: T:

$Formula: \begin{array}{rll} T & = & \dfrac{2 \pi}{\omega} \\[5pt] & = & 2\pi \cdot \sqrt{\dfrac{m}{A \cdot \rho \cdot g}} \end{array}$ $Formula: \begin{array}{rll} T & = & \dfrac{2 \pi}{\omega} \\[5pt] & = & 2\pi \cdot \sqrt{\dfrac{m}{A \cdot \rho \cdot g}} \end{array}$

Dies entspricht der angegebenen Gleichung.

Gegeben sind folgende Daten der Boje:

$Formula: m = 4900 \; \mathrm{kg}$ $Formula: m = 4900 \; \mathrm{kg}$

$Formula: d=2,55 \; \mathrm{m}$ $Formula: d=2,55 \; \mathrm{m}$

Außerdem besitzt die Boje eine zylindrische Form, somit ergibt sich für die Querschnittsfläche Formula: A :

$Formula: \begin{array}{rll}A & = & \pi \cdot r^2 \\[5pt]& = & \pi \cdot \left(\dfrac{d}{2}\right)^2 \\[5pt]& = & \pi \cdot \left(\dfrac{2,55 \; \mathrm{m}}{2}\right)^2 \\[5pt]& = & 5,11 \; \mathrm{m}^2\end{array}$ $Formula: \begin{array}{rll}A & = & \pi \cdot r^2 \\[5pt]& = & \pi \cdot \left(\dfrac{d}{2}\right)^2 \\[5pt]& = & \pi \cdot \left(\dfrac{2,55 \; \mathrm{m}}{2}\right)^2 \\[5pt]& = & 5,11 \; \mathrm{m}^2\end{array}$

Die Dichte $Formula: \rho$ $Formula: \rho$ des Wassers beträgt:

$Formula: \begin{array}{rll}\rho & = & 1,0 \; \frac{\mathrm{g}}{\mathrm{cm}^3} \\[5pt]& = & 1,0 \; \frac{\mathrm{kg}}{\mathrm{dm}^3} \\[5pt]& = & 1,0 \cdot 10^3 \; \frac{\mathrm{kg}}{\mathrm{m}^3}\end{array}$ $Formula: \begin{array}{rll}\rho & = & 1,0 \; \frac{\mathrm{g}}{\mathrm{cm}^3} \\[5pt]& = & 1,0 \; \frac{\mathrm{kg}}{\mathrm{dm}^3} \\[5pt]& = & 1,0 \cdot 10^3 \; \frac{\mathrm{kg}}{\mathrm{m}^3}\end{array}$

Diese Zahlenwerte lassen sich in die Formel für Formula: T aus b) einsetzen:

$Formula: \begin{array}{rll}T & = & 2\pi \cdot \sqrt{\dfrac{m}{A \cdot \rho \cdot g}} \\[5pt]& = & 2\pi \cdot \sqrt{\dfrac{4900}{5,11 \cdot 1,0 \cdot 10^3 \cdot 9,81}} \; \mathrm{s} \\[5pt]& = & 1,96 \; \mathrm{s}\end{array}$ $Formula: \begin{array}{rll}T & = & 2\pi \cdot \sqrt{\dfrac{m}{A \cdot \rho \cdot g}} \\[5pt]& = & 2\pi \cdot \sqrt{\dfrac{4900}{5,11 \cdot 1,0 \cdot 10^3 \cdot 9,81}} \; \mathrm{s} \\[5pt]& = & 1,96 \; \mathrm{s}\end{array}$

Es gilt $Formula: f=\frac{1} {T},$ $Formula: f=\frac{1} {T},$ somit beträgt die Frequenz der Boje:

$Formula: f = \frac{1}{T} = \frac{1}{1,96 \; \mathrm{s}} = 0,51 \; \frac{1}{\mathrm{s}}.$ $Formula: f = \frac{1}{T} = \frac{1}{1,96 \; \mathrm{s}} = 0,51 \; \frac{1}{\mathrm{s}}.$

Wenn die Erregerfrequenz Formula: f_e mit der Eigenfrequenz Formula: f_0 des Oszillators übereinstimmt, kommt es zu Resonanz und die Amplitude erreicht ihr Maximum. Umso mehr die Erregerfrequenz von der Eigenfrequenz abweicht, desto geringer ist die Amplitude.

Gesucht ist die Frequenz Formula: f der Wasserwellen. Es gilt:

$Formula: f = \frac{c}{\lambda}.$ $Formula: f = \frac{c}{\lambda}.$

M 6 lassen sich sowohl $Formula: \lambda$ $Formula: \lambda$ als auch Formula: c entnehmen:

$Formula: \begin{array}{rll}c & = & 22,0 \; \dfrac{\mathrm{km}}{\mathrm{h}} \\[5pt]& = & \dfrac{22,0}{3,6} \; \dfrac{\mathrm{m}}{\mathrm{s}} \\[5pt]& = & 6,11 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$ $Formula: \begin{array}{rll}c & = & 22,0 \; \dfrac{\mathrm{km}}{\mathrm{h}} \\[5pt]& = & \dfrac{22,0}{3,6} \; \dfrac{\mathrm{m}}{\mathrm{s}} \\[5pt]& = & 6,11 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$

$Formula: \lambda=12 \; \mathrm{m}.$ $Formula: \lambda=12 \; \mathrm{m}.$

Somit ergibt sich für die Frequenz Formula: f der Wasserwellen:

$Formula: f = \frac{c}{\lambda} = \frac{6,11}{12} \; \frac{1}{\mathrm{s}} = 0,51 \; \frac{1}{\mathrm{s}}.$ $Formula: f = \frac{c}{\lambda} = \frac{6,11}{12} \; \frac{1}{\mathrm{s}} = 0,51 \; \frac{1}{\mathrm{s}}.$

Diese Frequenz stimmt mit der in Aufgabe 3 c) berechneten Eigenfrequenz Formula: f_0 der Boje überein, somit kommt es zu Resonanz. Dadurch könnten diese Wasserwellen die Boje zu starken Schwingungen anregen, obwohl sie selbst nur eine Amplitude von $Formula: 20 \; \mathrm{cm}$ $Formula: 20 \; \mathrm{cm}$ besitzen.

Starke Schwingungen können durch Ändern der Eigenfrequenz $Formula: \mathrm{f}_0$ vermieden werden.

Mit Hilfe der aus Aufgabe 3 c) stammenden Formel für die Periodendauer $Formula: \mathrm{ T }$ $Formula: \mathrm{ T }$ und dem Zusammenhang $Formula: f=\frac{1}{T},$ $Formula: f=\frac{1}{T},$ ergibt sich für die Eigenfrequenz $Formula: \mathrm{f}_0$ der Boje:

$Formula: \begin{array}{rll}f & = & \dfrac{1}{T} \\[5pt]& = & \dfrac{1}{2\pi} \cdot \sqrt{\dfrac{A \cdot \rho \cdot g}{m}} \\[5pt]& = & \dfrac{\sqrt{\rho \cdot g}}{2\pi} \cdot \sqrt{\dfrac{A}{m}}\end{array}$ $Formula: \begin{array}{rll}f & = & \dfrac{1}{T} \\[5pt]& = & \dfrac{1}{2\pi} \cdot \sqrt{\dfrac{A \cdot \rho \cdot g}{m}} \\[5pt]& = & \dfrac{\sqrt{\rho \cdot g}}{2\pi} \cdot \sqrt{\dfrac{A}{m}}\end{array}$

Da $Formula: \tfrac{\sqrt{\rho \cdot \mathrm{g}}}{2 \pi}$ $Formula: \tfrac{\sqrt{\rho \cdot \mathrm{g}}}{2 \pi}$ nur aus Konstanten besteht, ergeben sich folgende Proportionalitäten:

$Formula: f \sim \sqrt{\frac{A}{1}}.$ $Formula: f \sim \sqrt{\frac{A}{1}}.$
$Formula: f \sim \sqrt{\frac{1}{m}}.$ $Formula: f \sim \sqrt{\frac{1}{m}}.$

Somit hängt die Eigenfrequenz Formula: f_0 der Boje von der Masse Formula: m und der Querschnittsfläche Formula: A der Boje ab und zwar mit $Formula: f \sim \sqrt{\tfrac{A}{m}}.$ $Formula: f \sim \sqrt{\tfrac{A}{m}}.$ Ziel ist es daher, den Quotient $Formula: \tfrac{A}{m}$ $Formula: \tfrac{A}{m}$ möglichst stark zu verändern. Eine Vergrößerung des Querschnitts bei gleichbleibendem Aufbau führt zu einer entsprechenden Vergrößerung der Masse, sodass der Quotient $Formula: \tfrac{A}{m}$ $Formula: \tfrac{A}{m}$ sich kaum ändert. Es wäre sinnvoller die Masse zu verringern und die Querschnittsfläche zu vergrößern oder die Masse zu vergrößern und die Querschnittsfläche zu verringern.

In der ersten Situation soll die Mole möglichst wenige Wellen durchlassen, in der zweiten Situation soll sie möglichst wenig das Ökosystem unter Wasser beeinträchtigen.

$Formula: \mathrm{I})$ $Formula: \mathrm{I})$	Geschlossene Mole: Sie reflektiert die auf sie treffenden Wellenenergie vollständig zurück. Somit wird das Hafenbecken stark von Wellen beruhigt. Allerdings ist der Bau der Mole ein starker Eingriff in das Ökosystem unter Wasser. Außerdem wird das Ökosystem durch Abschneiden des Hafens vom offenen Meerwasser verändert.
$Formula: \mathrm{II})$ $Formula: \mathrm{II})$	Schwimmmole: Hier ist die Dämpfung der Wellen geringer, da ein Teil der Wellenenergie unter der Mole oder dadurch dass sie selbst etwas beweglich ist weitergegeben wird. Dafür bleibt das Wasser mit dem offenen Meer verbunden und der Meeresboden bleibt nahezu unberührt.

Somit ist die geschlossene Mole für Situation I) besser geeignet, da sie die Wellen besser dämpft. Für Situation II) ist die Schwimmmole jedoch besser geeignet, da sie das Ökosystem weniger beeinträchtigt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?