Aufgabe 3 — Abstandsradarsysteme beim Auto

Moderne Autos besitzen Fahrerassistenzsysteme, bei denen ein Radar verwendet wird. Dieses befindet sich an der Front des Autos und dient hauptsächlich der Abstandsmessung.

Radarsysteme in Fahrzeugen arbeiten mit elektromagnetischen Wellen im Frequenzbereich zwischen $Formula: 20\; \mathrm{GHz}$ $Formula: 20\; \mathrm{GHz}$ und $Formula: 80\; \mathrm{GHz}$ $Formula: 80\; \mathrm{GHz}$ .

Ermittle mithilfe von Material 1, welchem Bereich des elektromagnetischen Spektrums die verwendeten Wellen zuzuordnen sind.

3 BE

Elektromagnetische Wellen können mit einem Schwingkreis erzeugt werden.

Erkläre die Entstehung von Schwingungen in einem elektromagnetischen Schwingkreis.

6 BE

Beurteile, ob es mit den in Material 2 aufgeführten handelsüblichen Bauteilen möglich ist, eine Schwingung in dem in Aufgabe 1 genannten Frequenzbereich zu erzeugen.

3 BE

Erkläre, dass man den Hertz’schen Dipol als Grenzfall eines elektromagnetischen Schwingkreises beschreiben kann und mit dem Hertz’schen Dipol große Frequenzen erzeugt werden können.

4 BE

In Material 3 ist die Arbeitsweise eines Abstandsradars näher beschrieben.

Begründe, dass die in Abbildung 3 dargestellten Signale zu der in Abbildung 2 fotografierten Verkehrssituation gehören könnten.

2 BE

Bestimme mithilfe des Diagramms in Material 3 den Abstand des LKW zum Radar.

2 BE

In einem Experiment soll die Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle untersucht werden. Ein zugehöriges Versuchsprotokoll ist in Material 4 gegeben.

Erkläre Beobachtung 1.

3 BE

Bestimme die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle aus Messung 1.

5 BE

Mit dem gleichen Versuchsaufbau wird die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle in einem Kunststoff bestimmt (siehe Durchführung 2).

Erkläre die Beobachtung 2.

4 BE

Bestätige mit Messung 2 und der Auswertung, dass die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle im verwendeten Kunststoff $Formula: c_M=1,9 \cdot 10^8 \; \tfrac{\mathrm{m}}{\mathrm{s}}$ $Formula: c_M=1,9 \cdot 10^8 \; \tfrac{\mathrm{m}}{\mathrm{s}}$ beträgt. Gehe dabei davon aus, dass $Formula: \Delta \ell<\tfrac{\lambda}{2}$ $Formula: \Delta \ell<\tfrac{\lambda}{2}$ in der Messung gilt.

3 BE

Begründe, dass die Einschränkung $Formula: \Delta \ell<\tfrac{\lambda}{2}$ $Formula: \Delta \ell<\tfrac{\lambda}{2}$ zur eindeutigen Bestimmung der Ausbreitungsgeschwindigkeit notwendig ist.

3 BE

Das in der Front verbaute Radarsystem eines Fahrzeugs hat zum Schutz vor Beschädigung eine Abdeckung aus dem in Aufgabe 4 verwendeten Kunststoff. Die Störung des Radarsignals ist besonders niedrig, wenn man die Dicke dieser Abdeckung so wählt, dass sie einer halben Wellenlänge in dem Kunststoff entspricht. Die Frequenz des Radars beträgt $Formula: 25\; \mathrm{GHz}.$ $Formula: 25\; \mathrm{GHz}.$

Berechne die Dicke einer geeigneten Abdeckung.

2 BE

Material 1: Informationen zum elektromagnetischen Spektrum

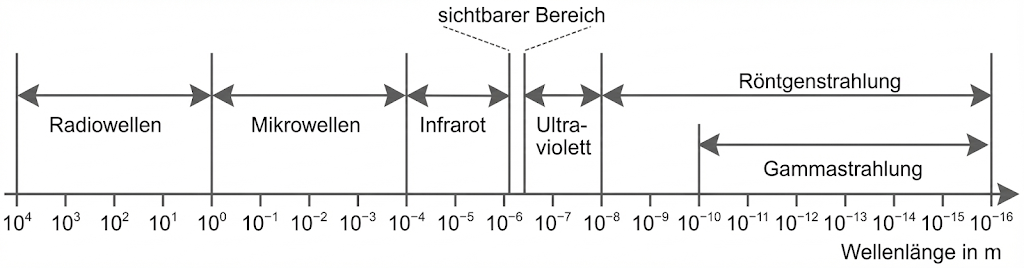
Elektromagnetisches Spektrum: Radiowellen, Mikrowellen, Infrarot, sichtbarer Bereich, Ultraviolett, Röntgen- und Gammastrahlung mit Wellenlängen

Abb. 1: elektromagnetisches Spektrum

Vorsätze bei Einheiten

Vorsatz	Wert
Kilo ( $Formula: \mathrm{k}$ $Formula: \mathrm{k}$ )
Mega ( $Formula: \mathrm{M}$ $Formula: \mathrm{M}$ )
Giga ( $Formula: \mathrm{G}$ $Formula: \mathrm{G}$ )
Terra ( $Formula: \mathrm{T}$ $Formula: \mathrm{T}$ )	$Formula: 10^{12}$ $Formula: 10^{12}$
Milli ( $Formula: \mathrm{m}$ $Formula: \mathrm{m}$ )	$Formula: 10^{-3}$ $Formula: 10^{-3}$
Mikro ( $Formula: \mathrm{\mu}$ $Formula: \mathrm{\mu}$ )	$Formula: 10^{-6}$ $Formula: 10^{-6}$
Nano ( $Formula: \mathrm{n}$ $Formula: \mathrm{n}$ )	$Formula: 10^{-9}$ $Formula: 10^{-9}$
Piko ( $Formula: \mathrm{p}$ $Formula: \mathrm{p}$ )	$Formula: 10^{-12}$ $Formula: 10^{-12}$

Tab. 1: Vorsätze

Material 2: Auszug aus einer Bestellliste

Artikelnummer	Artikelbezeichnung	Größe	Preis
312 182	Kondensator	$Formula: 4,7 \; \mathrm{pF}$ $Formula: 4,7 \; \mathrm{pF}$	14,00 € zzgl. MwSt.
312 23	Kondensator	$Formula: 220 \; \mathrm{pF}$ $Formula: 220 \; \mathrm{pF}$	14,00 € zzgl. MwSt.
312 262	Kondensator	$Formula: 3,3 \; \mathrm{nF}$ $Formula: 3,3 \; \mathrm{nF}$	14,00 € zzgl. MwSt.
722 84	Spule mit 1000 Windungen	$Formula: 18 \; \mathrm{mH}$ $Formula: 18 \; \mathrm{mH}$	51,60 € zzgl. MwSt.
722 83	Spule mit 500 Windungen	$Formula: 4,4 \; \mathrm{mH}$ $Formula: 4,4 \; \mathrm{mH}$	49,80 € zzgl. MwSt.

Tab. 2: Auszug aus dem Katalog eines Lehrmittelherstellers

Material 3: Abstandsbestimmung beim Abstandsradar

Aus einem Auto heraus wurde die in Abbildung 2 dargestellte Verkehrssituation fotografiert. Diese Verkehrssituation wurde gleichzeitig vom Radarsystem des Autos registriert. Dazu wurde vom Radar zum Zeitpunkt $Formula: t=0 \; \mathrm{s}$ $Formula: t=0 \; \mathrm{s}$ für eine kurze Zeitspanne eine elektromagnetische Welle ausgesendet, welche auch als Radarpuls bezeichnet wird. Trifft der Radarpuls auf einen Gegenstand, so kann von ihm ein „Echo“ zurückgeworfen werden. Dieses Echo wird vom Radarsystem aufgezeichnet und die Zeit zwischen Aussendung und Empfang wird gemessen. Die Echos der beiden Fahrzeuge sind in Abbildung 3 vereinfacht dargestellt.

Autobahn mit Pkw und Lkw, Bäume beidseits, Leitplanke und bewölkter Himmel

Abb. 2: Verkehrssituation

Foto: KI-generiert mit Nano Banana Pro

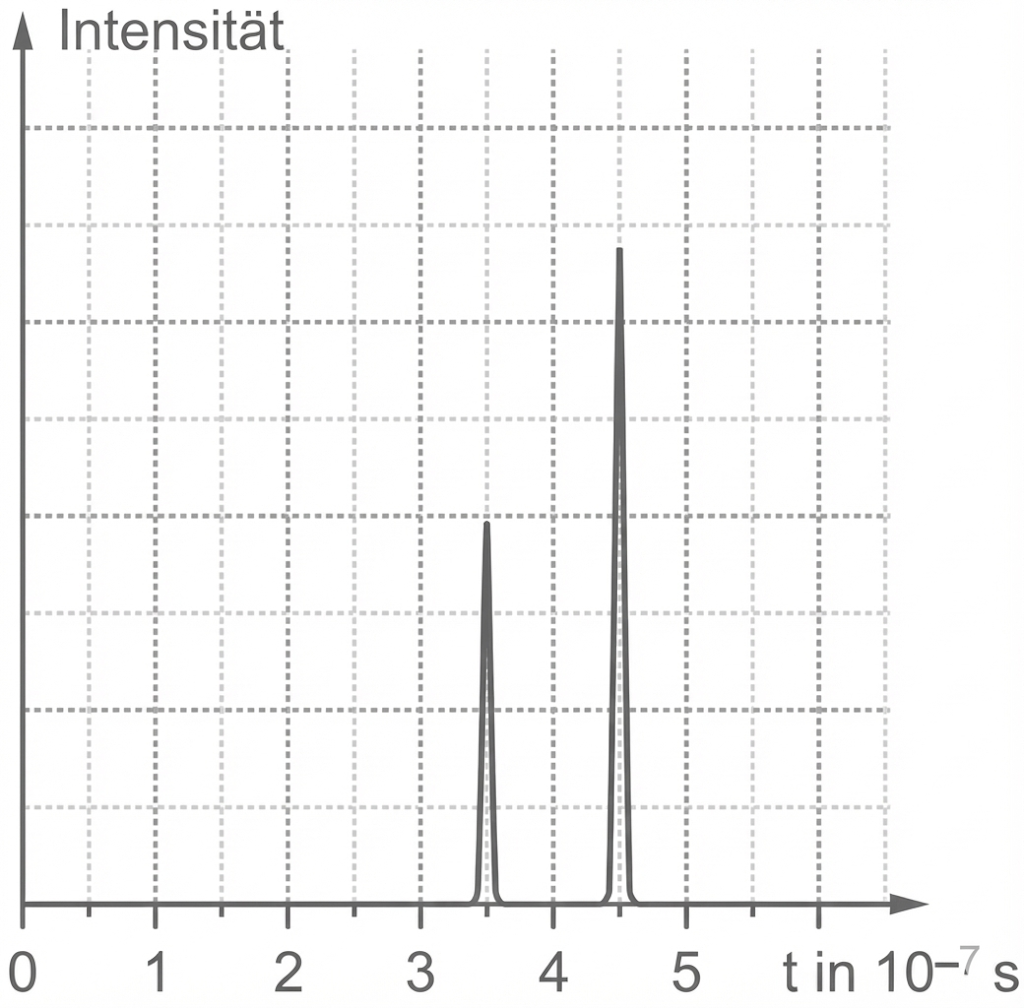
Diagramm Intensität gegen Zeit mit zwei schmalen Spitzen bei etwa 3·10^-7 s und 4·10^-7 s

Abb. 3: Radarsignale

Material 4: Versuchsprotokoll

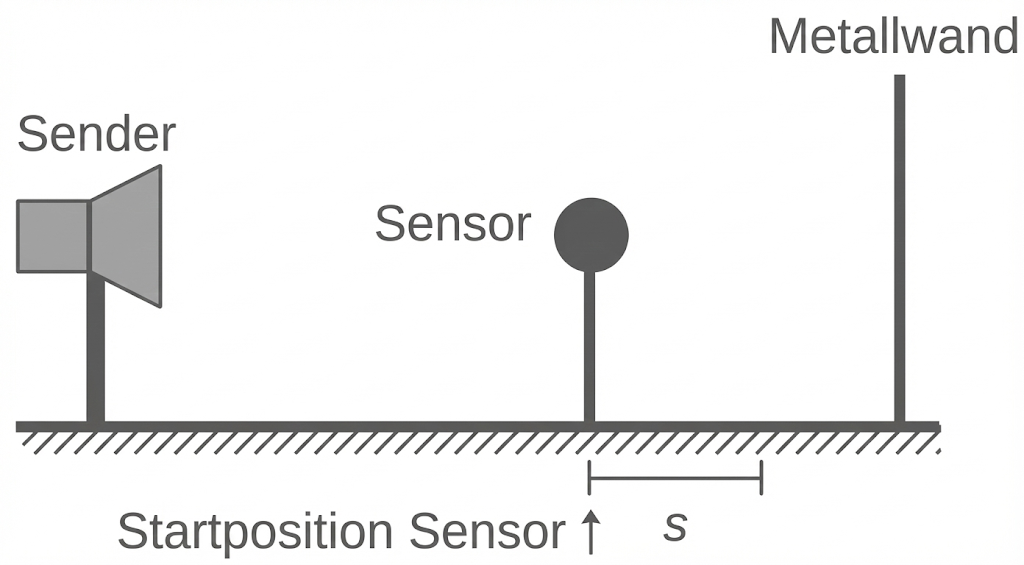
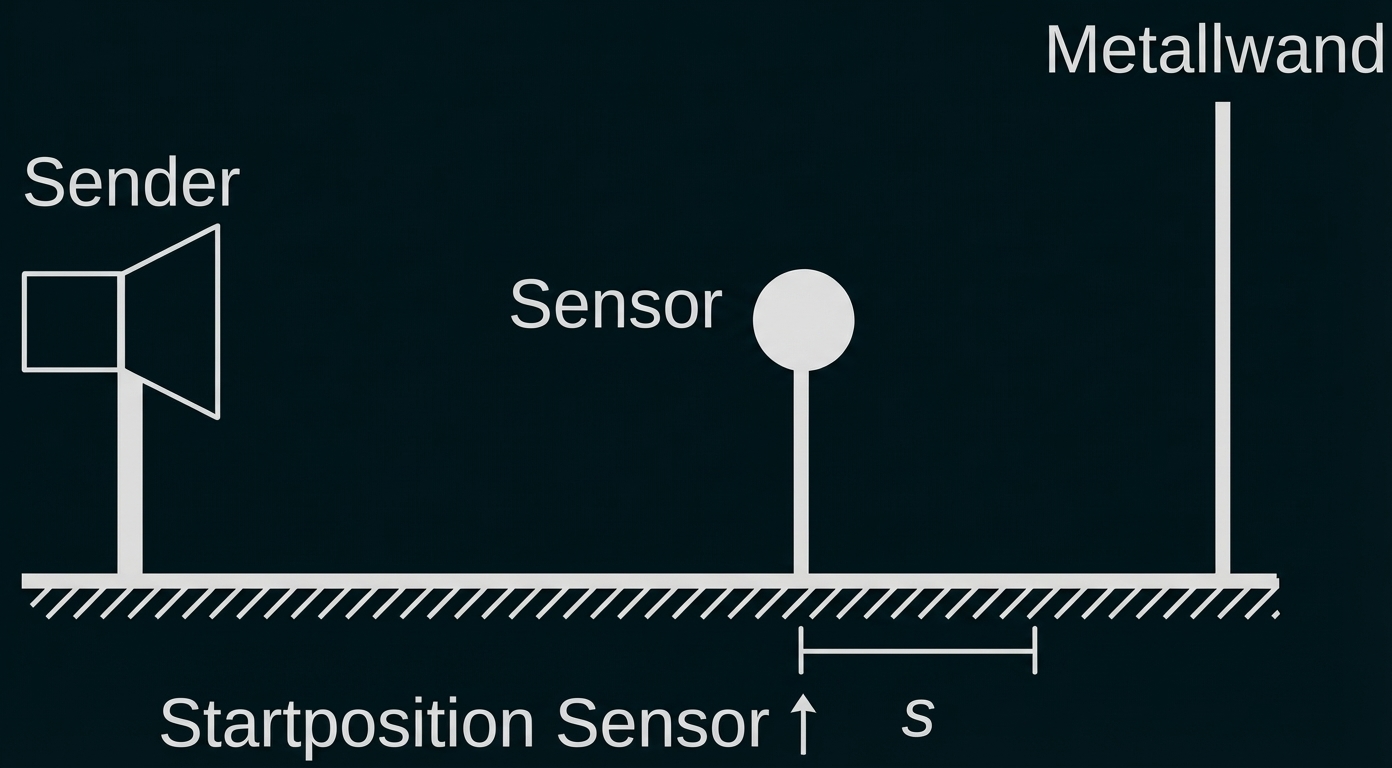
Versuchsaufbau

Ein Sender erzeugt elektromagnetische Wellen mit einer Frequenz von $Formula: 11,8 \; \mathrm{GHz},$ $Formula: 11,8 \; \mathrm{GHz},$ welche senkrecht auf eine Metallwand treffen. Die Intensität der Wellen wird mit einem beweglichen Sensor an unterschiedlichen Orten untersucht.

Schema: Sender links, Sensor mittig, Metallwand rechts, Bodenlinie und markierter Abstand s zur Startposition

Durchführung 1

Der Sensor wird entlang der Strecke $Formula: \mathrm{s}$ $Formula: \mathrm{s}$ vor der Metallwand bewegt und misst die Intensität.

Beobachtung 1

Wird der Sensor entlang der Strecke $Formula: \mathrm{s}$ $Formula: \mathrm{s}$ vor der Metallwand bewegt, dann werden regelmäßig auftretende Minima der Intensität registriert.

Messung 1

Position Sensor	$Formula: \boldsymbol{s}$ $Formula: \boldsymbol{s}$ in $Formula: \boldsymbol{\mathrm{mm}}$ $Formula: \boldsymbol{\mathrm{mm}}$
Startposition
1. Minimum
2. Minimum
3. Minimum
4. Minimum

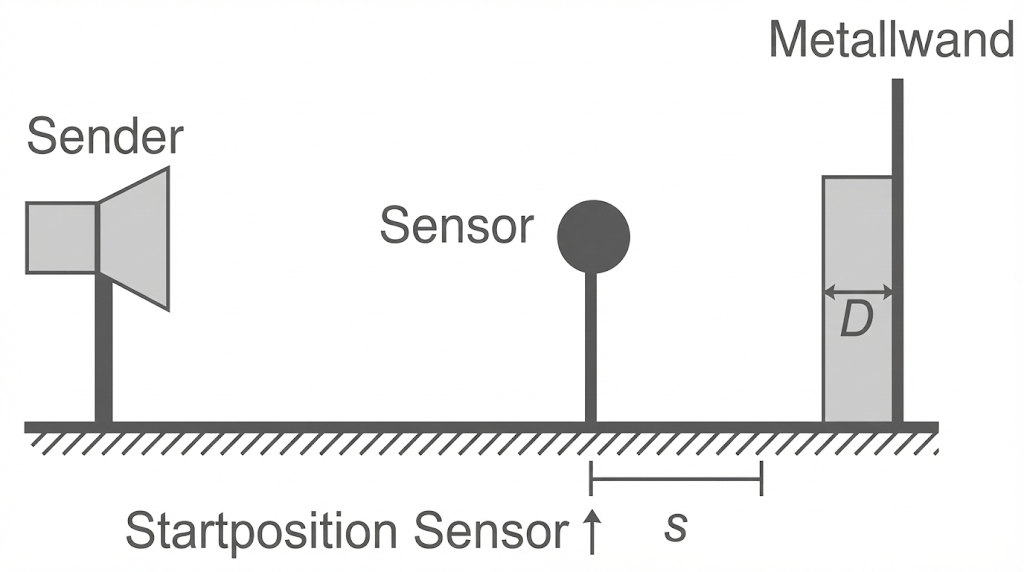
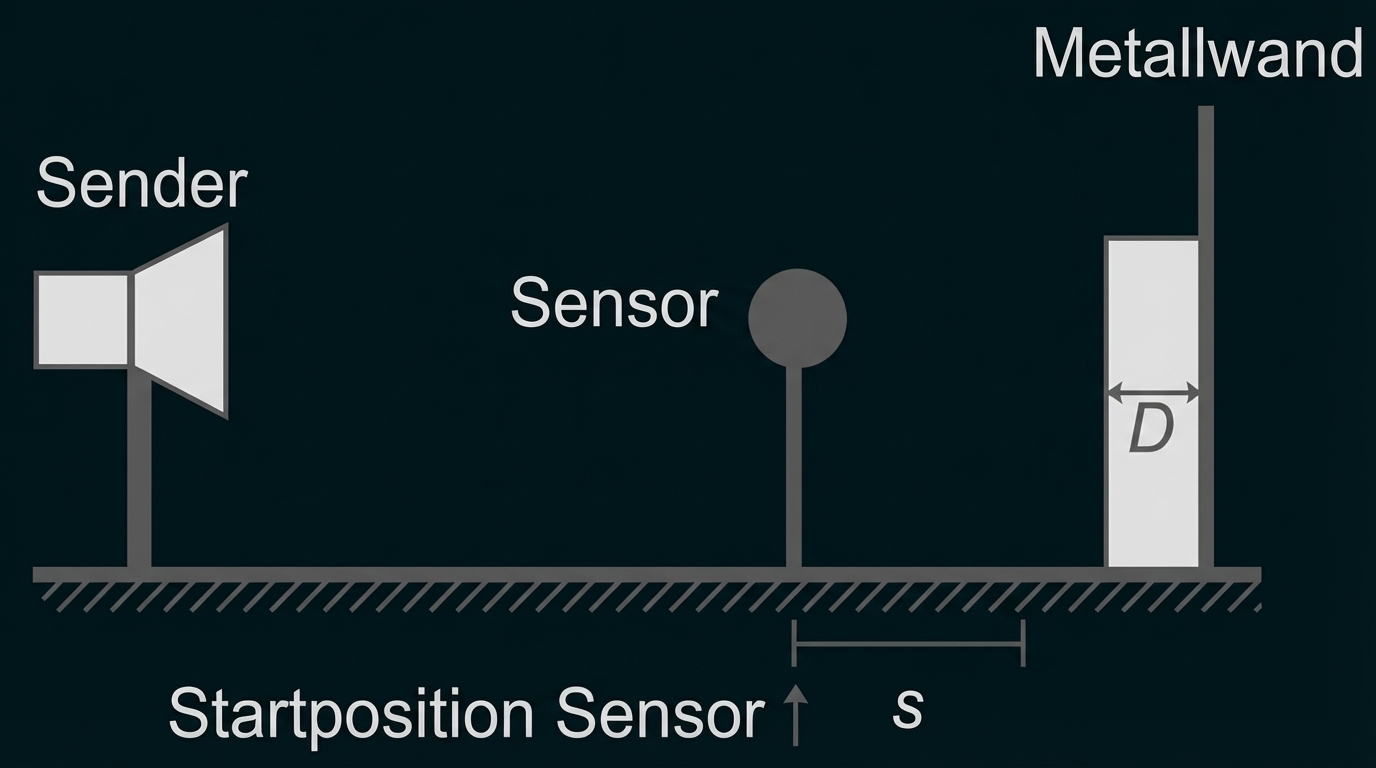
Durchführung 2

Eine Kunststoffplatte der Dicke $Formula: D=8 \; \mathrm{mm}$ $Formula: D=8 \; \mathrm{mm}$ wird direkt vor die Metallwand gebracht. Mit dem Sensor wird erneut die Position der Minima untersucht.

Schematische Darstellung: Sender links, Sensor in der Mitte, Metallwand rechts mit Abstand D und Startposition s.

Beobachtung 2

Die gemessenen Minima sind im Vergleich zu Messung 1 verschoben.

Messung 2

Position Sensor	$Formula: \boldsymbol{s}$ $Formula: \boldsymbol{s}$ in $Formula: \boldsymbol{\mathrm{mm}}$ $Formula: \boldsymbol{\mathrm{mm}}$
Startposition
1. Minimum
2. Minimum
3. Minimum
4. Minimum

Auswertung

Für die Lichtgeschwindigkeit $Formula: \mathrm{c}_{\mathrm{M}}$ $Formula: \mathrm{c}_{\mathrm{M}}$ im Kunststoff gilt für $Formula: \Delta \ell<\tfrac{\lambda}{2}$ $Formula: \Delta \ell<\tfrac{\lambda}{2}$

$Formula: c_M = c \cdot \dfrac{D}{D + \Delta \ell}$ $Formula: c_M = c \cdot \dfrac{D}{D + \Delta \ell}$ ,

wobei Formula: c die Lichtgeschwindigkeit im Vakuum, Formula: D die Dicke der Kunststoffplatte und $Formula: \Delta \ell$ $Formula: \Delta \ell$ die Verschiebung der Intensitätsminima ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Gesucht ist der Bereich der Wellenlängen $Formula: \lambda$ $Formula: \lambda$ der elektromagnetischen Wellen des Radarsystems. Es gilt $Formula: \lambda = \tfrac{c}{f}.$ $Formula: \lambda = \tfrac{c}{f}.$

Die größte Frequenz des angegebenen Frequenzbereichs lautet $Formula: f_1 = 80 \; \mathrm{GHz},$ $Formula: f_1 = 80 \; \mathrm{GHz},$ somit gilt für $Formula: \lambda_1$ $Formula: \lambda_1$ :

$Formula: \begin{array}{rll}\lambda_1 & = & \dfrac{c}{f_1} \\[5pt]& = & \dfrac{3,00 \cdot 10^8}{80 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 0,0038 \; \mathrm{m} \\[5pt]& = & 3,8 \cdot 10^{-3} \; \mathrm{m}\end{array}$ $Formula: \begin{array}{rll}\lambda_1 & = & \dfrac{c}{f_1} \\[5pt]& = & \dfrac{3,00 \cdot 10^8}{80 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 0,0038 \; \mathrm{m} \\[5pt]& = & 3,8 \cdot 10^{-3} \; \mathrm{m}\end{array}$

Die kleinste Frequenz des angegebenen Frequenzbereichs lautet $Formula: f_2 = 20 \; \mathrm{GHz},$ $Formula: f_2 = 20 \; \mathrm{GHz},$ somit gilt für $Formula: \lambda_2$ $Formula: \lambda_2$ :

$Formula: \begin{array}{rll}\lambda_2 & = & \dfrac{c}{f_2} \\[5pt]& = & \dfrac{3,00 \cdot 10^8}{20 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 0,015 \; \mathrm{m} \\[5pt]& = & 1,5 \cdot 10^{-2} \; \mathrm{m}\end{array}$ $Formula: \begin{array}{rll}\lambda_2 & = & \dfrac{c}{f_2} \\[5pt]& = & \dfrac{3,00 \cdot 10^8}{20 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 0,015 \; \mathrm{m} \\[5pt]& = & 1,5 \cdot 10^{-2} \; \mathrm{m}\end{array}$

In Material 1 lässt sich erkennen, dass dieser Wellenlängenbereich den Mikrowellen zugeordnet wird, somit ist der verwendete Frequenzbereich von $Formula: 20 \; \mathrm{GHz}$ $Formula: 20 \; \mathrm{GHz}$ bis $Formula: 80 \; \mathrm{GHz}$ $Formula: 80 \; \mathrm{GHz}$ den Mikrowellen zuzuordnen.

Ein Schwingkreis besteht aus einem Kondensator und einer Spule, die miteinander verbunden sind. Zu Beginn, zum Zeitpunkt $Formula: t=0 \; \mathrm{s},$ $Formula: t=0 \; \mathrm{s},$ ist der Kondensator vollständig aufgeladen und die gesamte Energie ist im elektrischen Feld des Kondensators gespeichert. Sobald der Kondensator über die Spule entladen wird, entsteht durch den Stromfluss in der Spule ein Magnetfeld, was bedeutet, dass ein Teil der zuvor elektrischen Energie in magnetische Energie umgewandelt wird. Die Lenz'sche Regel verhindert dabei den sofortigen Anstieg des Stroms durch die Spule, indem eine Gegenspannung induziert wird, die den Anstieg der Stromstärke hemmt.

Zum Zeitpunkt $Formula: t = \tfrac{1}{4} \; T$ $Formula: t = \tfrac{1}{4} \; T$ (mit als der Periodendauer der Schwingung) ist der Kondensator vollständig entladen und die maximale Stromstärke $Formula: I_{\mathrm{max}}$ $Formula: I_{\mathrm{max}}$ fließt durch die Spule. In dieser Phase ist die gesamte Energie im magnetischen Feld der Spule gespeichert.

Durch den Abfall der Stromstärke induziert das Magnetfeld der Spule wieder eine Gegenspannung, wodurch sich der Kondensator mit umgekehrter Polarität wieder auflädt, während der Strom in der Spule langsam sinkt und die Energie wieder ins elektrische Feld des Kondensators zurückgeht. Das geht bis zum Zeitpunkt $Formula: t = \tfrac{1}{2}\; T,$ $Formula: t = \tfrac{1}{2}\; T,$ an dem die gesamte Energie wieder im elektrischen Feld des Kondensators steckt.

Dieser Vorgang wiederholt sich nun in umgekehrter Richtung, bis der Kondensator zum Zeitpunkt $Formula: t = 1 \; T$ $Formula: t = 1 \; T$ wieder vollständig aufgeladen ist und der Schwingkreis wieder seine Ausgangslage erreicht hat.

Die Frequenz eines Schwingkreises hängt von der Kapazität Formula: C des Kondensators und der Induktivität Formula: L der Spule ab und wird folgende Formel bestimmt:

$Formula: f = \frac{1}{2\pi \cdot \sqrt{L \cdot C}}.$ $Formula: f = \frac{1}{2\pi \cdot \sqrt{L \cdot C}}.$

Es sollen sehr hohe Frequenzen Formula: f erreicht werden, somit müssen laut der Formel Bauteile mit möglichst kleinen Werten verwendet werden. Mit diesen Werten erhält man eine maximal erzeugbare Frequenz $Formula: f_{\max }$ $Formula: f_{\max }$ von:

$Formula: \begin{array}{rll}f_{\mathrm{max}} & = & \dfrac{1}{2\pi \cdot \sqrt{L_{\mathrm{min}} \cdot C_{\mathrm{min}}}} \\[5pt]& = & \dfrac{1}{2\pi \cdot \sqrt{4,4 \cdot 10^{-3} \cdot 4,7 \cdot 10^{-12}}} \; \mathrm{Hz} \\[5pt]& = & 1,1 \cdot 10^6 \; \mathrm{Hz} \\[5pt]& = & 1,1 \; \mathrm{MHz}\end{array}$ $Formula: \begin{array}{rll}f_{\mathrm{max}} & = & \dfrac{1}{2\pi \cdot \sqrt{L_{\mathrm{min}} \cdot C_{\mathrm{min}}}} \\[5pt]& = & \dfrac{1}{2\pi \cdot \sqrt{4,4 \cdot 10^{-3} \cdot 4,7 \cdot 10^{-12}}} \; \mathrm{Hz} \\[5pt]& = & 1,1 \cdot 10^6 \; \mathrm{Hz} \\[5pt]& = & 1,1 \; \mathrm{MHz}\end{array}$

Diese Frequenz liegt deutlich unterhalb des gewünschten Frequenzbereichs von $Formula: 20 \mathrm{GHz}$ $Formula: 20 \mathrm{GHz}$ bis $Formula: 80 \mathrm{GHz}$ $Formula: 80 \mathrm{GHz}$ , was bedeutet, dass die gegebenen handelsüblichen Bauteile nicht dafür geeignet sind, um den Frequenzbereich aus Aufgabe 1 zu erreichen.

Ein Hertz’scher Dipol kann als Grenzfall eines Schwingkreises betrachtet werden, mit einer Spule mit minimaler Windungszahl und einem Kondensator mit kleinen Plattenflächen und großem Plattenabstand. Die Spule wird dabei zu einem Draht und die Kondensatorplatten werden die beiden Enden des Drahtes. In diesem Fall ist die Induktivität Formula: L der Spule (minimale Windungszahl) und die Kapazität Formula: C des Kondensators (kleine Plattenflächen und großer Plattenabstand) sehr klein, was nach $Formula: f = \tfrac{1}{2\pi \cdot \sqrt{L \cdot C}}$ $Formula: f = \tfrac{1}{2\pi \cdot \sqrt{L \cdot C}}$ zu einer sehr hohen Frequenz des Schwingkreises führt.

In Abbildung 3 des Materials sind zwei Radarimpulse mit unterschiedlichen Laufzeiten und Intensitäten zu sehen. Das schwächere Signal mit der kürzeren Laufzeit könnte vom PKW stammen, der sich in geringerem Abstand zum Radar befindet. Das stärkere Signal mit der längeren Laufzeit könnte hingegen vom LKW stammen, der sich weiter entfernt befindet. Die größere Fläche des LKW reflektiert jedoch mehr Radarwellen, was zu einer stärkeren Signalintensität führt.

Das Radar erfasst das Signal des LKW mit einer Hin- und Rücklaufzeit von $Formula: t=4,5 \cdot 10^{-7} \; \mathrm{s}$ $Formula: t=4,5 \cdot 10^{-7} \; \mathrm{s}$ . Die Formel zur Berechnung des Abstands Formula: s lautet:

$Formula: s = c \cdot \frac{t}{2}.$ $Formula: s = c \cdot \frac{t}{2}.$

Nun setzt man die Werte ein:

$Formula: s = c \cdot \frac{t}{2} = 3,00 \cdot 10^8 \cdot 2,25 \cdot 10^{-7} \; \mathrm{m} = 68 \; \mathrm{m}.$ $Formula: s = c \cdot \frac{t}{2} = 3,00 \cdot 10^8 \cdot 2,25 \cdot 10^{-7} \; \mathrm{m} = 68 \; \mathrm{m}.$

Der LKW befindet sich also in einem Abstand von $Formula: 68 \; \mathrm{m}$ $Formula: 68 \; \mathrm{m}$ vom Radar.

Es werden vom Sender aus Wellen ausgesendet, die an der Metallwand reflektiert werden. Außerdem wird die Intensität der Wellen mit einem Sensor gemessen. Wenn der Sensor entlang der Strecke $Formula: \mathrm{s}$ $Formula: \mathrm{s}$ bewegt wird, registriert er regelmäßig auftretende Minima. Diese Minima entstehen aufgrund der stehenden Welle, die durch die Superposition (Überlagerung) der ursprünglichen und reflektierten Wellen erzeugt werden. Die benachbarten Minima besitzen immer den konstanten Abstand einer halben Wellenlänge zueinander.

Die gemessenen Intensitätsminima geben Hinweise auf die Wellenlänge der elektromagnetischen Wellen. Die Abstände benachbarter Minima in Messung 1 betragen durchschnittlich $Formula: s = \tfrac{38 \; \mathrm{mm}}{3} = 12,66 \; \mathrm{mm}.$ $Formula: s = \tfrac{38 \; \mathrm{mm}}{3} = 12,66 \; \mathrm{mm}.$ Die Wellenlänge kann somit berechnet werden:

$Formula: \lambda = 2 \cdot 12,66 \; \mathrm{mm} = 25,3 \; \mathrm{mm}.$ $Formula: \lambda = 2 \cdot 12,66 \; \mathrm{mm} = 25,3 \; \mathrm{mm}.$

Die Ausbreitungsgeschwindigkeit der Welle wird mit $Formula: c=\lambda \cdot f$ $Formula: c=\lambda \cdot f$ berechnet. Somit beträgt die Ausbreitungsgeschwindigkeit:

$Formula: \begin{array}{rll}c & = & \lambda \cdot f \\[5pt]& = & 0,0253 \cdot 11,8 \cdot 10^9 \; \dfrac{\mathrm{m}}{\mathrm{s}} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$ $Formula: \begin{array}{rll}c & = & \lambda \cdot f \\[5pt]& = & 0,0253 \cdot 11,8 \cdot 10^9 \; \dfrac{\mathrm{m}}{\mathrm{s}} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$

Da sich weiterhin die einlaufenden und reflektierten Wellen überlagern, entsteht wieder eine stehende Welle. In dem Kunststoff breiten sich die Wellen jedoch langsamer aus, während die Periodendauer der stehenden Welle dadurch aber nicht beeinflusst wird. Somit verringert sich im Kunststoff die Wellenlänge der Wellen, wodurch sich die Minima näher bei der Platte ausbilden. Dadurch dass die Dicke der Platte kleiner ist als die halbe Wellenlänge, bilden sich keine Minima in der Kunststoffplatte, wodurch die Anzahl der Minima und ihr Abstand zueinander unverändert bleibt. Somit verschiebt sich das Wellenmuster in Messung 2 gegenüber Messung 1 etwas Richtung Metallwand.

Die durchschnittliche Verschiebung $Formula: \Delta \ell$ $Formula: \Delta \ell$ der Minima muss zunächst berechnet werden:

$Formula: \Delta \ell = \frac{(5+4+5+4) \; \mathrm{mm}}{4} = 4,5 \; \mathrm{mm}.$ $Formula: \Delta \ell = \frac{(5+4+5+4) \; \mathrm{mm}}{4} = 4,5 \; \mathrm{mm}.$

Da laut Aufgabenstellung $Formula: \Delta \ell<\frac{\lambda}{2}$ $Formula: \Delta \ell<\frac{\lambda}{2}$ gilt, kann die Formel aus Material 4 angewendet werden:

$Formula: \begin{array}{rll}c_{\mathrm{M}} & = & c \cdot \dfrac{D}{D+\Delta \ell} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}} \cdot \dfrac{8 \; \mathrm{mm}}{8 \; \mathrm{mm} + 4,5 \; \mathrm{mm}} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}} \cdot \dfrac{8}{12,5} \\[5pt]& = & 1,9 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$ $Formula: \begin{array}{rll}c_{\mathrm{M}} & = & c \cdot \dfrac{D}{D+\Delta \ell} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}} \cdot \dfrac{8 \; \mathrm{mm}}{8 \; \mathrm{mm} + 4,5 \; \mathrm{mm}} \\[5pt]& = & 3,0 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}} \cdot \dfrac{8}{12,5} \\[5pt]& = & 1,9 \cdot 10^8 \; \dfrac{\mathrm{m}}{\mathrm{s}}\end{array}$

Somit beträgt die Ausbreitungsgeschwindigkeit der Wellen in Kunststoff $Formula: c_M=1,9 \cdot 10^8 \; \frac{\mathrm{m}}{\mathrm{s}}.$ $Formula: c_M=1,9 \cdot 10^8 \; \frac{\mathrm{m}}{\mathrm{s}}.$

Um die Ausbreitungsgeschwindigkeit im Kunststoff eindeutig zu bestimmen, muss die Verschiebung der Minima zunächst eindeutig bestimmt werden. Rein theoretisch könnte es aber sein, dass die Minima nicht nur um $Formula: 4,5 \; \mathrm{mm}$ $Formula: 4,5 \; \mathrm{mm}$ , sondern um eine weitere halbe Wellenlänge verschoben worden sind. Um das auszuschließen, ist die Einschränkung $Formula: \Delta \ell<\frac{\lambda}{2}$ $Formula: \Delta \ell<\frac{\lambda}{2}$ notwendig.

Mit der Ausbreitungsgeschwindigkeit im Kunststoff Formula: c_M aus Aufgabe 4 c) ergibt sich für die Wellenlänge in Kunststoff $Formula: \lambda_M:$ $Formula: \lambda_M:$

$Formula: \begin{array}{rll}\lambda_{\mathrm{M}} & = & \dfrac{c_{\mathrm{M}}}{f} \\[5pt]& = & \dfrac{1,9 \cdot 10^8}{25 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 7,6 \cdot 10^{-3} \; \mathrm{m} \\[5pt]& = & 7,6 \; \mathrm{mm}\end{array}$ $Formula: \begin{array}{rll}\lambda_{\mathrm{M}} & = & \dfrac{c_{\mathrm{M}}}{f} \\[5pt]& = & \dfrac{1,9 \cdot 10^8}{25 \cdot 10^9} \; \mathrm{m} \\[5pt]& = & 7,6 \cdot 10^{-3} \; \mathrm{m} \\[5pt]& = & 7,6 \; \mathrm{mm}\end{array}$

Da $Formula: D=\tfrac{1}{2} \cdot \lambda_M$ $Formula: D=\tfrac{1}{2} \cdot \lambda_M$ sein soll, ergibt sich für die Dicke der Kunststoffabdeckung:

$Formula: D = \frac{1}{2} \cdot \lambda_{\mathrm{M}} = \frac{1}{2} \cdot 7,6 \; \mathrm{mm} = 3,8 \; \mathrm{mm}.$ $Formula: D = \frac{1}{2} \cdot \lambda_{\mathrm{M}} = \frac{1}{2} \cdot 7,6 \; \mathrm{mm} = 3,8 \; \mathrm{mm}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?