Aufgabe 2 – Licht
1.
In einem Praktikumsversuch sollen der Spaltmittenabstand und die Spaltbreite eines Doppelspalts bestimmt werden. Dazu wird ein Laserstrahl der Wellenlänge  orthogonal zur Doppelspaltebene gerichtet. Ein Schirm wird nacheinander in unterschiedlichen Entfernungen parallel zur Doppelspaltebene aufgestellt. Die Abbildung 1 zeigt einen Ausschnitt des auf dem Schirm entstehenden Interferenzmusters in Originalgröße für einen Schirmabstand von
orthogonal zur Doppelspaltebene gerichtet. Ein Schirm wird nacheinander in unterschiedlichen Entfernungen parallel zur Doppelspaltebene aufgestellt. Die Abbildung 1 zeigt einen Ausschnitt des auf dem Schirm entstehenden Interferenzmusters in Originalgröße für einen Schirmabstand von  .
.



Abbildung 1
a)
Erkläre das Zustandekommen der Intensitätsminima in Abbildung 
b)
Leite anhand geeigneter Skizzen eine Gleichung für den Abstand dieser Intensitätsminima zum Maximum nullter Ordnung auf dem Schirm her.
c)
Bestimme den Spaltmittenabstand des Doppelspalts.
Nun wird der Schirm bei sonst gleichen Versuchsbedingungen verschoben. Abbildung 2 zeigt das Interferenzmuster in Originalgröße.

Abbildung 2
d)
Ermittle diesen Schirmabstand.
e)
Erkläre, weshalb nicht alle Maxima dieselbe Intensität aufweisen.
f)
Bestimme die Breite der beiden Spalte des Doppelspalts.
(12 VP)
2.
Laserlicht der Wellenlänge  trifft senkrecht auf ein Gitter mit 570 Strichen pro Millimeter, welches mittig an der Wand eines Aquariums angebracht ist. Abbildung 3 zeigt die Versuchsanordnung von oben. Von Reflexion und Brechung an den Glasscheiben ist abzusehen.
trifft senkrecht auf ein Gitter mit 570 Strichen pro Millimeter, welches mittig an der Wand eines Aquariums angebracht ist. Abbildung 3 zeigt die Versuchsanordnung von oben. Von Reflexion und Brechung an den Glasscheiben ist abzusehen.
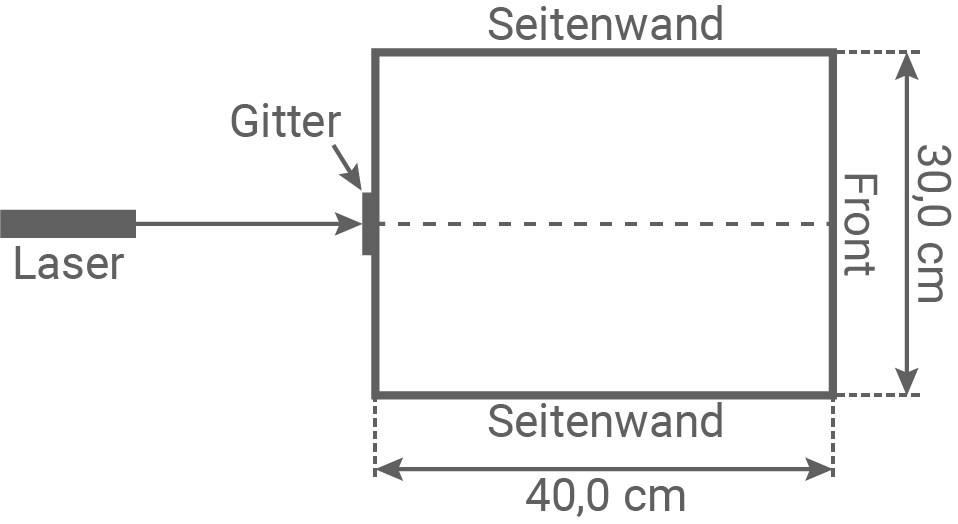
Abbildung 3
a)
Berechne die Anzahl der Leuchtpunkte auf beiden Seitenwänden.
Um die Interferenz im Inneren des Aquariums beobachten zu können, wird das Aquarium vollständig mit Wasser gefüllt und einige Tropfen Milch dazugegeben. Durch Streuung im milchigen Wasser werden helle Linien sichtbar. Abbildung 4 zeigt beispielhaft eine solche Erscheinung.

Abbildung 4
b)
Erkläre den näherungsweise geradlinigen Verlauf dieser Linien.
Durch das eingefülte Wasser hat sich die Gesamtzahl der Leuchtpunkte auf der Front und den Seitenwänden vergrößert.
c)
Erkläre diesen Sachverhalt.
Man kann in dem milchigen Wasser 9 Linien beobachten.
d)
Bestimme den Bereich, in dem die Wellenlänge des Laserlichts in Wasser liegen muss.
(9 VP)
3.
Eine Fotozelle wird mit monochromatischem Licht bestrahlt. Die Ablöseenergie dieser Fotozelle beträgt  Zwischen dem Anodenring und der Kathode misst man eine Spannung von
Zwischen dem Anodenring und der Kathode misst man eine Spannung von  (siehe Abb. 5).
(siehe Abb. 5).
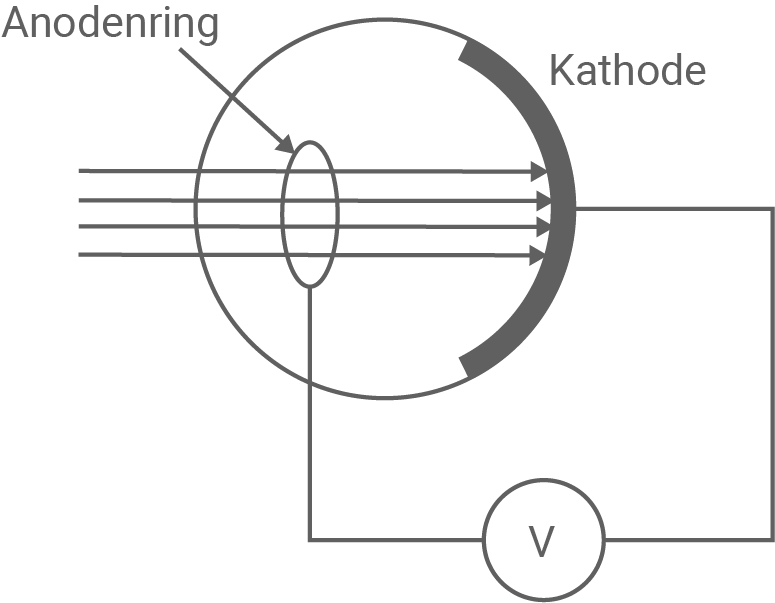
Abbildung 5
a)
Berechne die Wellenlänge des monochromatischen Lichts.
b)
Erläutere, ob man mit dieser Fotozelle die Wellenlänge beliebigen monochromatischen Lichts bestimmen kann.
Um die Abhängigkeit der Wellenlänge von der gemessenen Spannung darzustellen, stehen die folgenden drei Diagramme zur Auswahl (siehe Abb. 6).
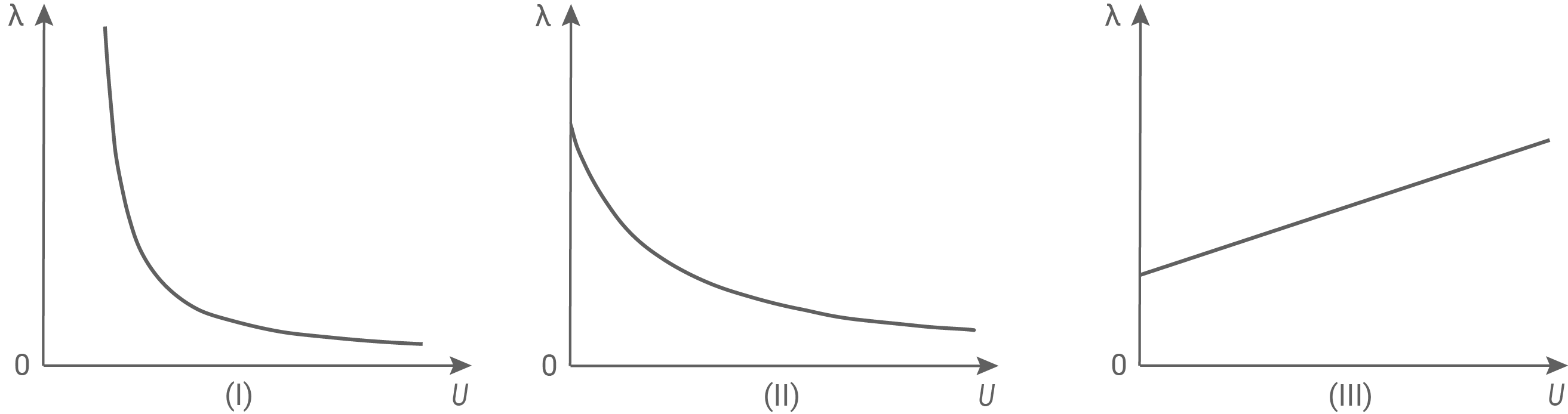
Abbildung 6
c)
Diskutiere für jedes Diagramm, ob die Abhängigkeit zwischen Wellenlänge und Spannung qualitativ richtig dargestellt wird.
Die Fotozelle wird mit dem Licht einer weißen LED beleuchtet. Das Spektrum der LED zeigt Abbildung 7.
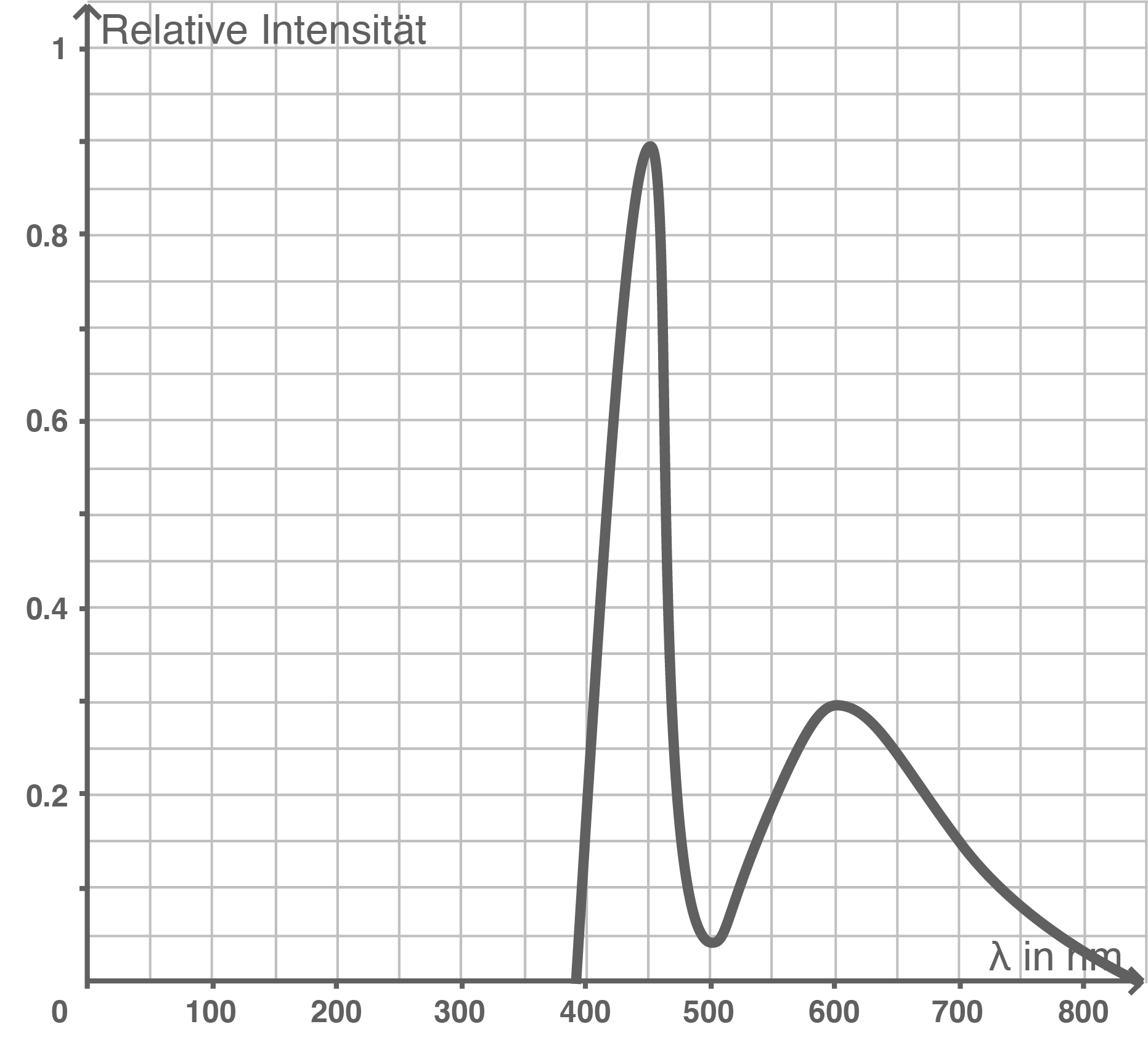
Abbildung 7
d)
Bestimme die Spannung zwischen den Anschlüssen der Fotozelle und begründe dein Vorgehen.
(9 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die beiden Öffnungen des Doppelspaltes sind Ausgangspunkte von Wellen, die auf dem Schirm mit einem gewissen Gangunterschied interferieren. An den dunklen Stellen löschen sich die von den Öffnungen ausgehenden Wellen aus, die Lichtintensität ist hier minimal.
b)
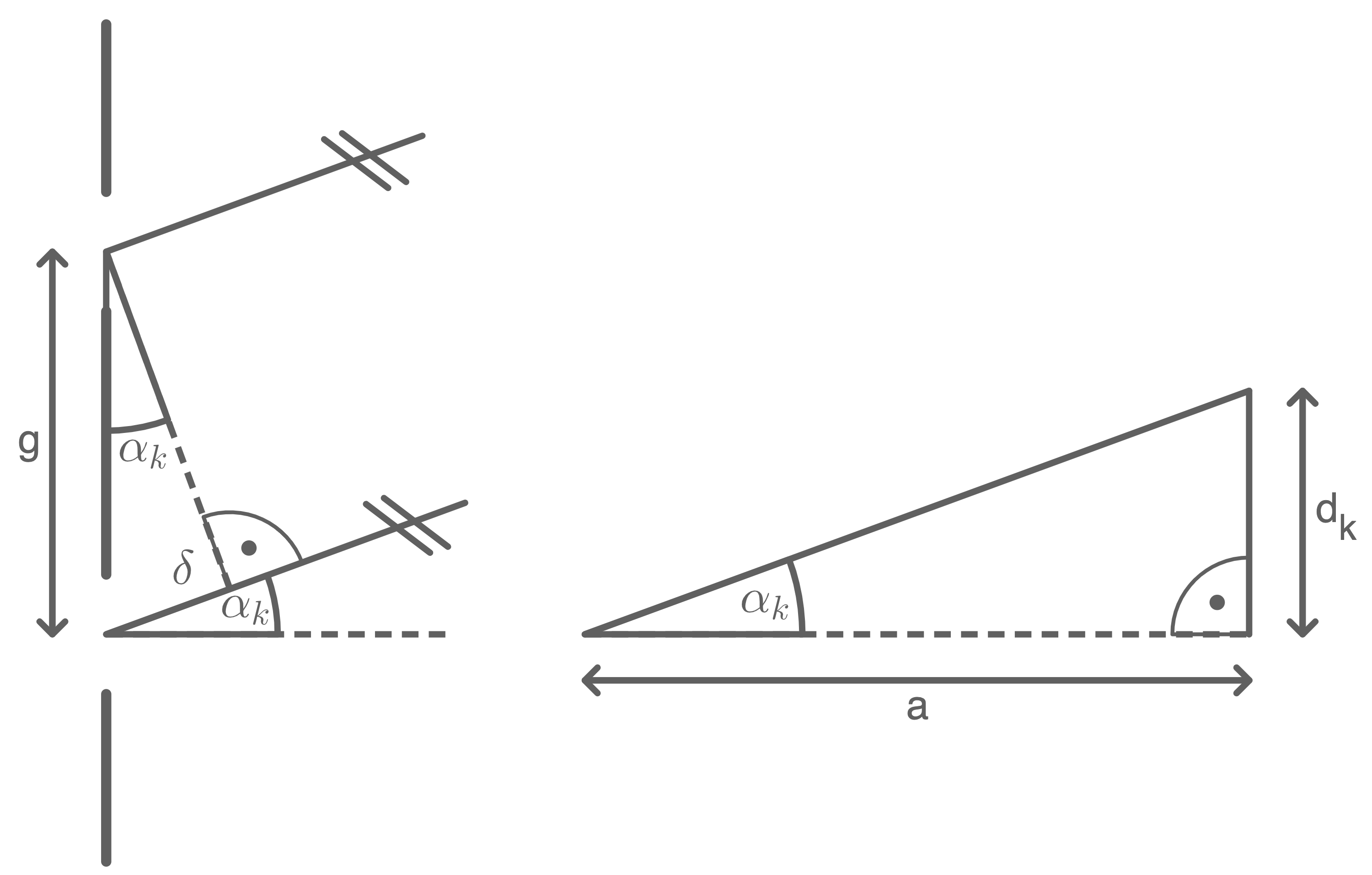
c)
Aus der Abbildung lässt sich der Abstand der beiden Minima 3. Ordnung ablesen. Er beträgt  das Minimum 3. Ordnung hat zur Schirmmitte den Abstand
das Minimum 3. Ordnung hat zur Schirmmitte den Abstand  . Somit ergibt sich:
. Somit ergibt sich:
![\(\begin{array}[t]{rll}
d_k &=& \dfrac{\delta}{g} \cdot a &\quad \scriptsize \mid\; \cdot \dfrac{g}{d_k} \\[5pt]
g &=& \dfrac{\delta}{d_{\mathrm{k}}} \cdot a \\[5pt]
g &=& \dfrac{(2 \mathrm{k}-1) \cdot \lambda}{d_{\mathrm{k}} \cdot 2} \cdot a \\[5pt]
g &=& \dfrac{(2 \cdot 3-1) \cdot 650 \mathrm{~nm}}{2,2 \mathrm{~cm} \cdot 2} \cdot 7,0 \mathrm{~m} \\[5pt]
g &=& 0,52 \mathrm{~mm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c599ab51c31f3bb847ffe06101c86246856e6b05660d271568644bd18c212aa4_light.svg)
d)
Beim neuen Schirmabstand haben die Minima 3. Ordnung nur einen Abstand von  , der Abstand des Minimums 3. Ordnung zur Schirmmitte beträgt
, der Abstand des Minimums 3. Ordnung zur Schirmmitte beträgt  Dies entspricht dem halben Abstand im Vergleich zum ersten Versuch.
Es ist
Dies entspricht dem halben Abstand im Vergleich zum ersten Versuch.
Es ist  womit
womit  (Ist
(Ist  nur noch halb so groß, gilt dies ebenfalls für
nur noch halb so groß, gilt dies ebenfalls für  Aus dieser Proportionalität des Abstands zur Schirmentfernung folgt, dass der Schirm nur halb so weit von der Doppelspaltebenen entfernt ist. Der Schirmabstand beträgt
Aus dieser Proportionalität des Abstands zur Schirmentfernung folgt, dass der Schirm nur halb so weit von der Doppelspaltebenen entfernt ist. Der Schirmabstand beträgt 
e)
Die beiden Öffnungen haben eine nicht vernachlässigbare Breite, es kommt zur Beugung des Lichts am Einzelspalt. In den Richtungen, bei denen sich dadurch eine verringerte Lichtintensität ergibt, besitzen auch die Maxima der Doppelspaltbeugung eine geringere Intensität im Vergleich zu den Maxima, die z.B. unter kleinen Winkeln im Bereich des Hauptmaximums der Einzelspaltbeugung auftreten.
f)
Aus Abbildung 2 kann abgelesen werden, dass das erste Minimum der Einzelspaltbeugung etwa  von der Schirmmitte entfernt ist. Da der Beugungswinkel klein ist, gilt:
von der Schirmmitte entfernt ist. Da der Beugungswinkel klein ist, gilt:
![\(\begin{array}[t]{rll}
\sin \alpha&\approx& \tan \alpha \\[5pt]
\dfrac{\lambda}{b} &=& \dfrac{d_1}{a} &\quad \scriptsize \mid\; \cdot \dfrac{b \cdot a}{d_1} \\[5pt]
\dfrac{\lambda}{d_{1}} \cdot a &=& b \\[5pt]
b &=& \dfrac{\lambda}{d_{1}} \cdot a \\[5pt]
b &=& \dfrac{650 \mathrm{~nm}}{2,2 \mathrm{~cm}} \cdot 3,5 \mathrm{~m} \\[5pt]
b &=& 0,1 \mathrm{~mm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/333e2766174211c46c7266a4d4a1c036fc1f54f6155ab2e8ff21c264cabbbba3_light.svg)
2
a)
Beim vorliegenden Gitter beträgt der Abstand der Öffnungen  .
Die Richtungswinkel zur optischen Achse zu den Maxima ergeben sich aus der Beziehung
.
Die Richtungswinkel zur optischen Achse zu den Maxima ergeben sich aus der Beziehung  mit
mit  Der größte mögliche Winkel für ein Maximum beträgt
Der größte mögliche Winkel für ein Maximum beträgt  , für die zugehörige Ordnung ergibt sich:
, für die zugehörige Ordnung ergibt sich:
![\(\begin{array}[t]{rll}
\sin (\alpha) &=& \dfrac{k \cdot \lambda}{g} &\quad \scriptsize \mid\; \cdot \dfrac{g}{\lambda} \\[5pt]
\sin (\alpha) \cdot \dfrac{g}{\lambda} &=& k \\[5pt]
k &=& \sin (\alpha) \cdot \dfrac{g}{\lambda} \\[5pt]
k &=& \sin (90^\circ) \cdot \dfrac{1,75 \cdot 10^{-6} \mathrm{~m}}{520 \mathrm{~nm}} \\[5pt]
k &=& 3,37 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5546f29f7d275059008318abe57c66435e4698062e6523387a6766e4f0ce32d5_light.svg) Damit entstehen bei diesem Gitter Maxima bis zur 3. Ordnung.
Der Richtungswinkel zu der Ecke des Aquariums beträgt:
Damit entstehen bei diesem Gitter Maxima bis zur 3. Ordnung.
Der Richtungswinkel zu der Ecke des Aquariums beträgt:
![\(\begin{array}[t]{rll}
\tan (\beta) &=& \dfrac{d_1}{a} \\[5pt]
\tan (\beta) &=& \dfrac{d_1}{a} \\[5pt]
\tan (\beta) &=& \dfrac{0,15 \mathrm{~m}}{0,4 \mathrm{~m}} &\quad \scriptsize \mid\; \arctan(\;) \\[5pt]
\beta &=& 20,6^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/31fee913b0b3007d4c82b50f13b66b93ff7c42684bda044a82a1fbdccdc058e5_light.svg) Der Richtungswinkel des 1. Maximums beträgt
Der Richtungswinkel des 1. Maximums beträgt
![\(\begin{array}[t]{rll}
\sin (\alpha_1)&=& \dfrac{1 \cdot \lambda}{g} \\[5pt]
\sin (\alpha_1)&=& \dfrac{1 \cdot \lambda}{g} \\[5pt]
\sin (\alpha_1)&=& \dfrac{1 \cdot 520 \text{ nm}}{1,75 \cdot 10^{-6} \mathrm{~m}} &\quad \scriptsize \mid\; \arcsin(\;) \\[5pt]
\alpha_1&=& 17,2^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/ebcd813a62d5172977edd48dcd38e4e0c1b7a3fa93050dea6b403b9a85091299_light.svg) Der Richtungswinkel des 2. Maximums beträgt
Der Richtungswinkel des 2. Maximums beträgt
![\(\begin{array}[t]{rll}
\sin (\alpha_2)&=& \dfrac{2 \cdot \lambda}{g} \\[5pt]
\sin (\alpha_2)&=& \dfrac{2 \cdot \lambda}{g} \\[5pt]
\sin (\alpha_2)&=& \dfrac{2 \cdot 520 \text{ nm}}{1,75 \cdot 10^{-6} \mathrm{~m}} &\quad \scriptsize \mid\; \arcsin(\;) \\[5pt]
\alpha_2&=& 34,1^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/776dea221a24642c5474d384951a70769084c6516e8e9a44f71d8bea34b05375_light.svg) Folglich liegt bereits das zweite Maximum auf der Seitenwand, da
Folglich liegt bereits das zweite Maximum auf der Seitenwand, da  ist. Somit sind auf den Seitenwänden des Aquariums vier Leuchtpunkte, die zu den Maxima 2. und 3. Ordnung gehören, beobachtbar.
ist. Somit sind auf den Seitenwänden des Aquariums vier Leuchtpunkte, die zu den Maxima 2. und 3. Ordnung gehören, beobachtbar.
b)
Jede Gitteröffnung ist Ausgangspunkt von Wellen. An jedem Ort in der Wanne, an dem sich die Wellen konstruktiv überlagern, wird Licht mit merklicher Intensität von den Milchteilchen gestreut. Die Orte maximaler Intensität im Aquarium findet man bei genügend großem Abstand zum Gitter unter den Richtungswinkeln  zur optischen Achse mit
zur optischen Achse mit  mit
mit  Die Wellenlänge ist dabei die Wellenlänge des Lichts im Wasser. Die im Wasser hell leuchtenden Stellen liegen folglich auf Geraden, die unter diesen Winkeln
Die Wellenlänge ist dabei die Wellenlänge des Lichts im Wasser. Die im Wasser hell leuchtenden Stellen liegen folglich auf Geraden, die unter diesen Winkeln  erscheinen.
erscheinen.
c)
Bei gleichbleibender Gitterkonstante lassen sich nach dem Füllen des Aquariums mit Wasser höhere Ordnungen der Gitterbeugung beobachten. Die Gleichung zur Bestimmung der maximal beobachtbaren Ordnungen  hat demnach eine Lösung
hat demnach eine Lösung  .
Das ist nur möglich, wenn die Wellenlänge
.
Das ist nur möglich, wenn die Wellenlänge  in Wasser kleiner ist als die Wellenlänge dieses Lichts in Luft. Die Frequenz des Lichts ändert sich mit dem Einfüllen des Wassers nicht. Aus der Beziehung
in Wasser kleiner ist als die Wellenlänge dieses Lichts in Luft. Die Frequenz des Lichts ändert sich mit dem Einfüllen des Wassers nicht. Aus der Beziehung  ergibt sich, dass die Lichtgeschwindigkeit
ergibt sich, dass die Lichtgeschwindigkeit  im Wasser kleiner als in Luft ist.
im Wasser kleiner als in Luft ist.
d)
Neun Lichtwege sind zu sehen, falls das Maximum 4. Ordnung gerade noch unter einem Richtungswinkel von  entsteht bzw. das Maximum 5. Ordnung gerade nicht mehr erscheint. Die obere Grenze für die Wellenlänge ergibt sich aus:
entsteht bzw. das Maximum 5. Ordnung gerade nicht mehr erscheint. Die obere Grenze für die Wellenlänge ergibt sich aus:
 Die untere Grenze für die Wellenlänge ist
Die untere Grenze für die Wellenlänge ist
 .
Die Wellenlänge des Laserlichts im Wasser liegt daher im Bereich zwischen
.
Die Wellenlänge des Laserlichts im Wasser liegt daher im Bereich zwischen  und
und  .
.
3
a)
Die Wellenlänge ergeben sich aus:
b)
Die Energie der Photonen muss größer sein als die Ablöseenergie der Elektronen in der Fotozelle. Somit gilt:
![\(\begin{array}[t]{rll}
E_A&\lt& h \cdot f \\[5pt]
E_A&\lt& h \cdot \dfrac{c}{\lambda} &\quad \scriptsize \mid\; \cdot \dfrac{\lambda}{E_A} \\[5pt]
\lambda &\lt& \dfrac{h \cdot c}{E_A}
\end{array}\)](https://www.schullv.de/resources/formulas/b984bd4280d9f391ad82ca0244627448fe16188a29c885fea79750580297abed_light.svg) Folglich funktioniert das Verfahren nicht mit Photonen des Lichts für beliebige Wellenlängen.
Folglich funktioniert das Verfahren nicht mit Photonen des Lichts für beliebige Wellenlängen.
c)
Bei Verwendung unterschiedlicher Lichtquellen stellen sich unterschiedliche Spannungen  an der Fotozelle ein. Die Wellenlänge ergibt sich aus der Spannung gemäß
an der Fotozelle ein. Die Wellenlänge ergibt sich aus der Spannung gemäß
 . (Siehe Teilaufgabe a). Dabei ist die Spannung größer oder gleich Null.
Diagramm (iii) stellt einen linearen Zusammenhang zwischen
. (Siehe Teilaufgabe a). Dabei ist die Spannung größer oder gleich Null.
Diagramm (iii) stellt einen linearen Zusammenhang zwischen  und
und  dar, ein solcher besteht offensichtlich nicht. Die Abbildung stellt den Zusammenhang nicht korrekt dar.
Die Spannung zwischen Anode und Kathode ist Null, wenn man Licht mit der Grenzwellenlänge zur Beleuchtung der Fotozelle benutzt (vgl. Teilaufgabe b)). Bei Diagramm (i) gehören zu sehr kleinen Werten der Spannung Wellenlängen, die jede Grenze überschreiten. Das passt nicht zum vorliegenden Experiment mit der Fotozelie. Nur das Diagramm (ii) kann zum Sachverhalt passen. Der Achsenabschnitt auf der
dar, ein solcher besteht offensichtlich nicht. Die Abbildung stellt den Zusammenhang nicht korrekt dar.
Die Spannung zwischen Anode und Kathode ist Null, wenn man Licht mit der Grenzwellenlänge zur Beleuchtung der Fotozelle benutzt (vgl. Teilaufgabe b)). Bei Diagramm (i) gehören zu sehr kleinen Werten der Spannung Wellenlängen, die jede Grenze überschreiten. Das passt nicht zum vorliegenden Experiment mit der Fotozelie. Nur das Diagramm (ii) kann zum Sachverhalt passen. Der Achsenabschnitt auf der  -Achse ist die Grenzwellenlänge, zu größeren Werten der Spannung gehören kleinere Wellenlängen.
-Achse ist die Grenzwellenlänge, zu größeren Werten der Spannung gehören kleinere Wellenlängen.
d)
Die Spannung hängt von der kleinsten Wellenlänge des einfallenden Lichtes ab, die zugehörigen Photonen besitzen die größte Energie. Dem Diagramm wird für die kleinste Wellenlänge ca.  entnommen. Es gilt:
entnommen. Es gilt: