Aufgabe 3 – Elektromagnetismus
1.
In einem Experiment wird der Betrag der magnetischen Flussdichte  eines homogenen Magnetfeldes bestimmt. Dazu wird ein rechteckiges Leiterrähmchen mit 500 Windungen so auf eine empfindliche Waage gestellt, dass sich der obere Teil vollständig im Magnetfeld befindet (siehe Abbildung 1).
eines homogenen Magnetfeldes bestimmt. Dazu wird ein rechteckiges Leiterrähmchen mit 500 Windungen so auf eine empfindliche Waage gestellt, dass sich der obere Teil vollständig im Magnetfeld befindet (siehe Abbildung 1).
Das Leiterrähmchen steht senkrecht zu den Feldlinien und wird von einem elektrischen Strom durchflossen, dessen Stärke verändert werden kann. Die von der Waage in Abhängigkeit von der Stromstärke angezeigten Werte sind in Tabelle 1 angegeben.
angezeigten Werte sind in Tabelle 1 angegeben.
Das Leiterrähmchen steht senkrecht zu den Feldlinien und wird von einem elektrischen Strom durchflossen, dessen Stärke verändert werden kann. Die von der Waage in Abhängigkeit von der Stromstärke
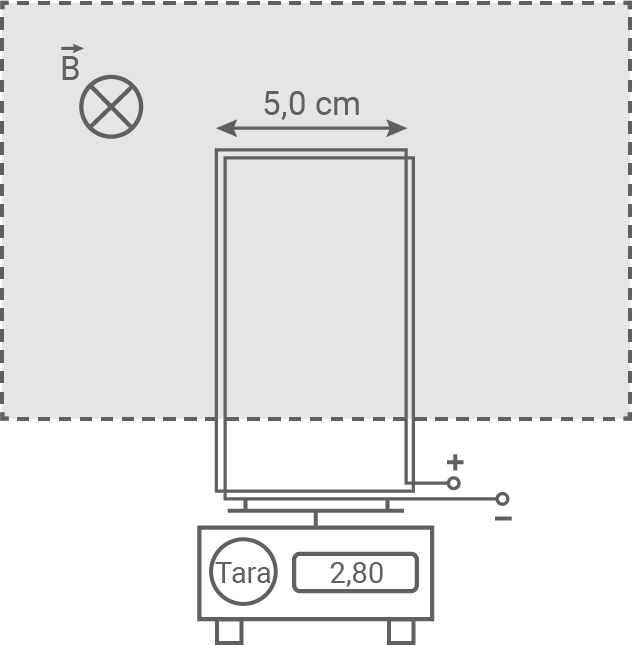
Abbildung 1
| I in mA | angezeigter Wert in g |
|---|---|
Tabelle 1
a)
Erläutere, weshalb die von der Waage angezeigten Werte mit zunehmender Stromstärke ansteigen.
b)
Berechne den Betrag der magnetischen Flussdichte für die Messung bei der Stromstärke 
c)
Stelle die magnetische Kraft auf das Leiterrähmchen in Abhängigkeit von der Stromstärke in einem Diagramm dar und ermittle daraus den Betrag der magnetischen Flussdichte.
d)
Vergleiche das Vorgehen aus b) und c) hinsichtlich der Genauigkeit bei der Bestimmung von 
(10 VP)
2.
Ein geladener Kondensator mit der Kapazität  wird mit einer Spule verbunden und die Spannung am Kondensator gemessen. Abbildung 2 zeigt den zugehörigen Spannungsverlauf.
wird mit einer Spule verbunden und die Spannung am Kondensator gemessen. Abbildung 2 zeigt den zugehörigen Spannungsverlauf.
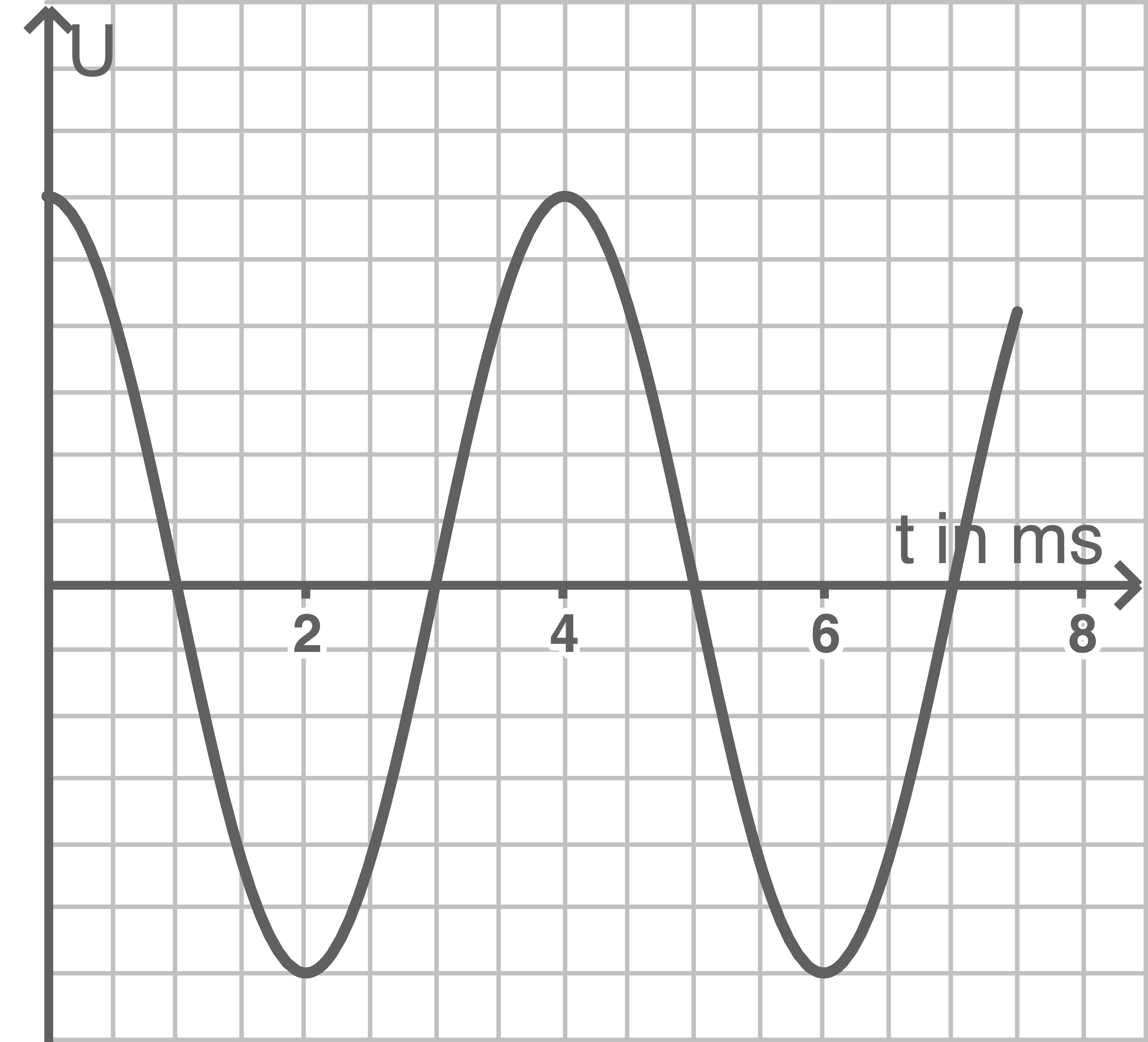

Abbildung 2
a)
Erläutere, weshalb eine Wechselspannung auftritt.
b)
Bestimme die Induktivität der Spule.
Zeitgleich zur Spannung am Kondensator wird auch die Stromstärke in der Spule bestimmt.
c)
Begründe, welche der folgenden vier Kurvenverläufe aus den Abbildungen 3a bis 3d sich bei der Messung nicht ergeben können.
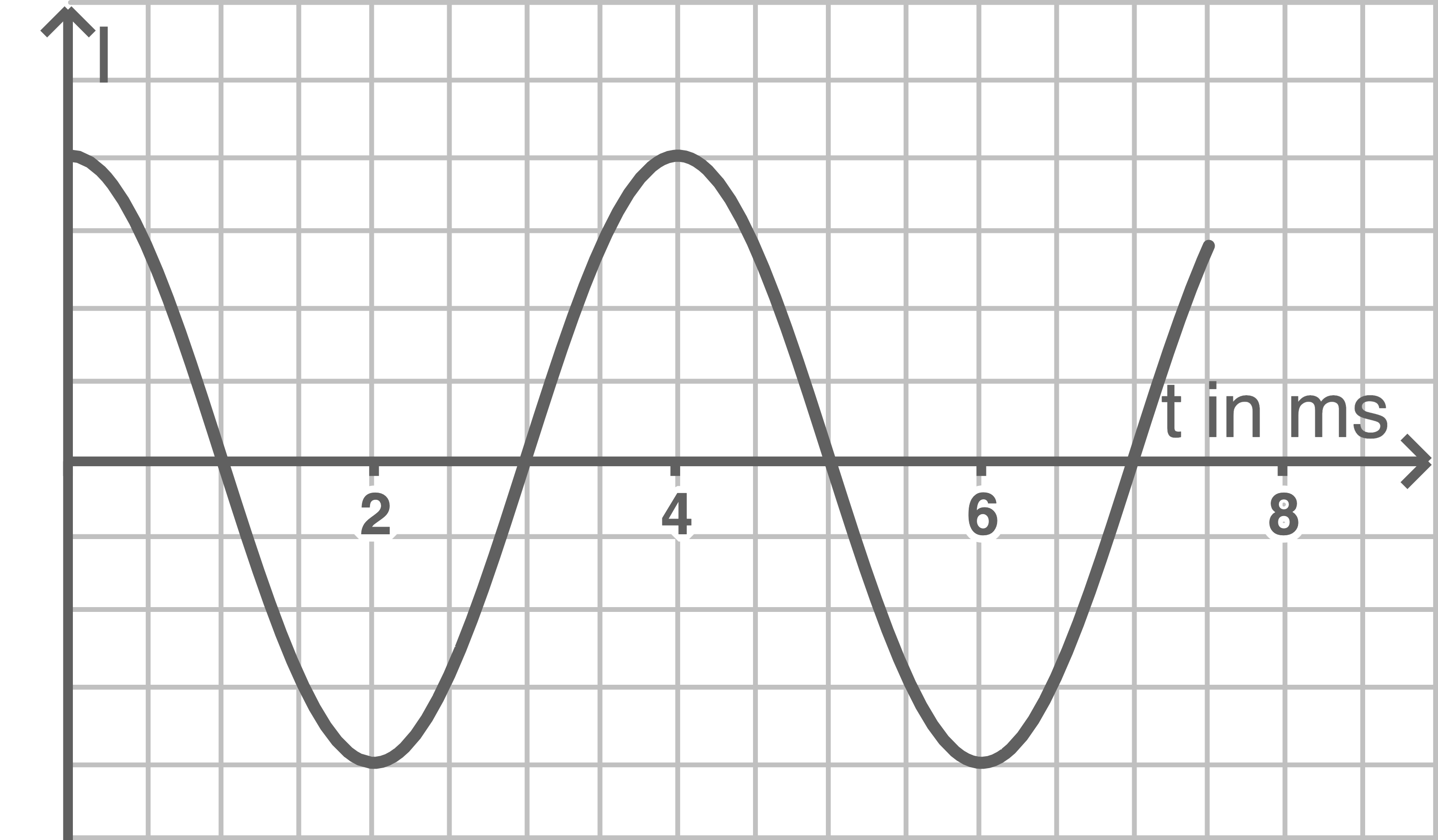
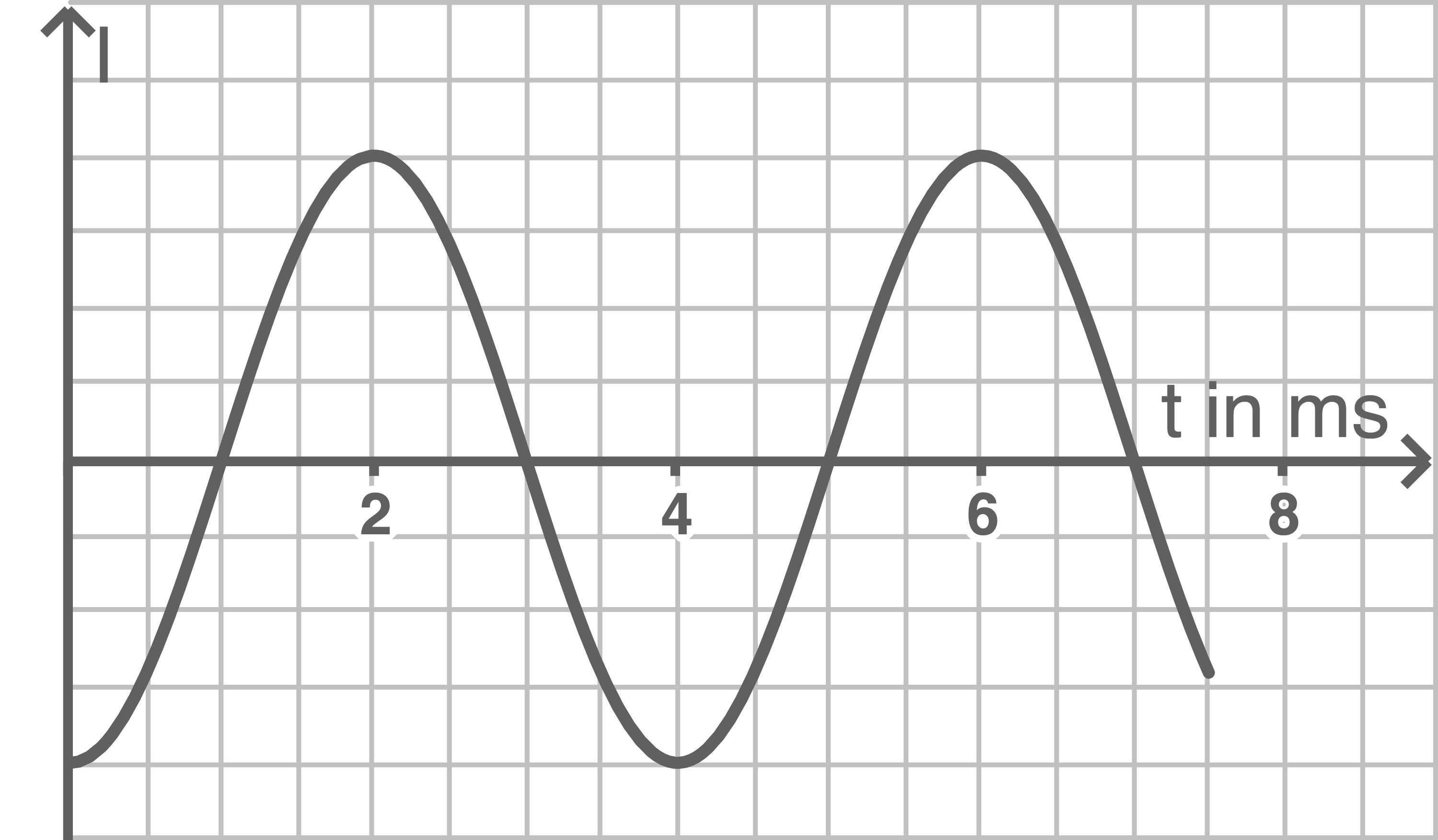
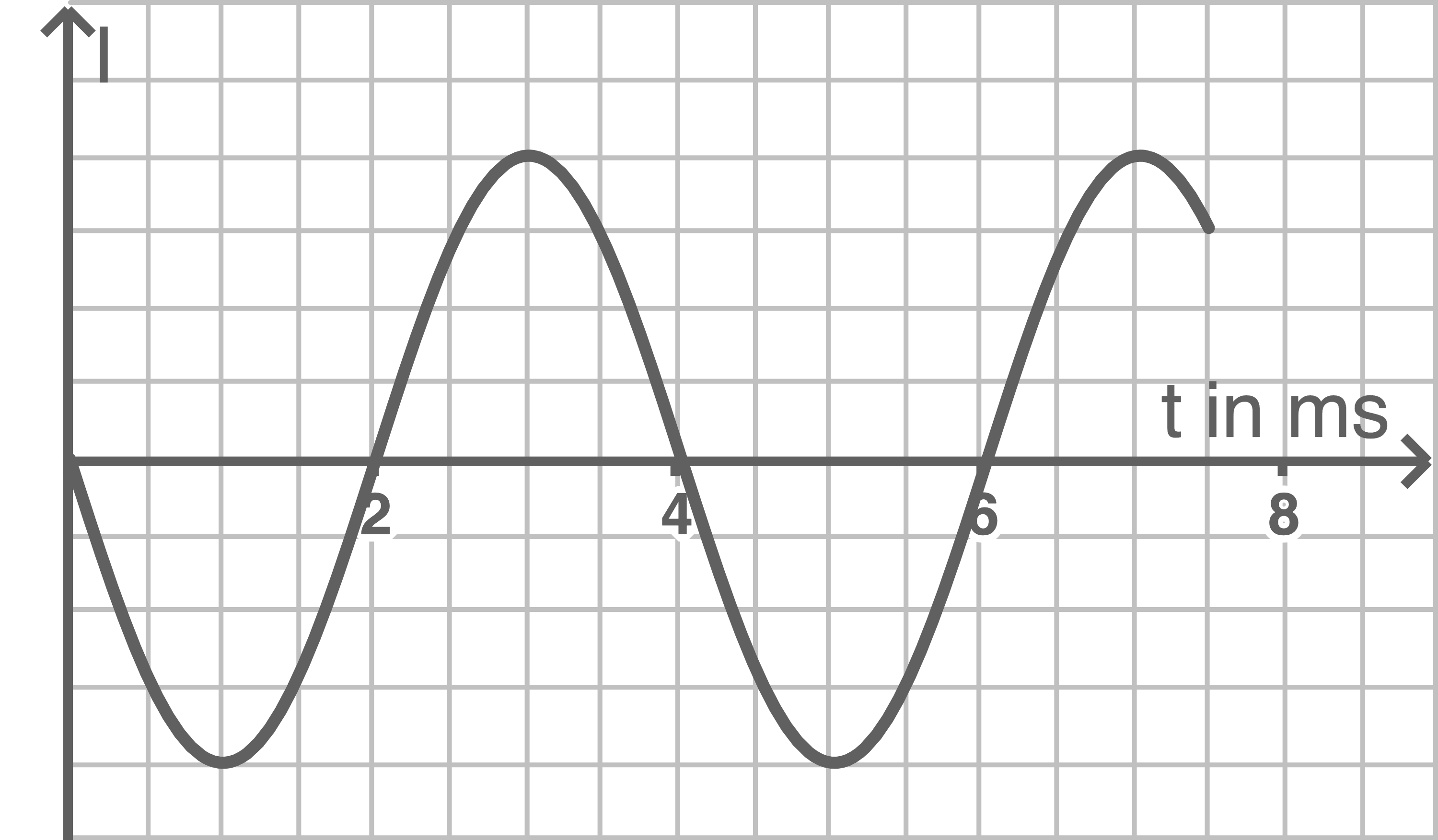
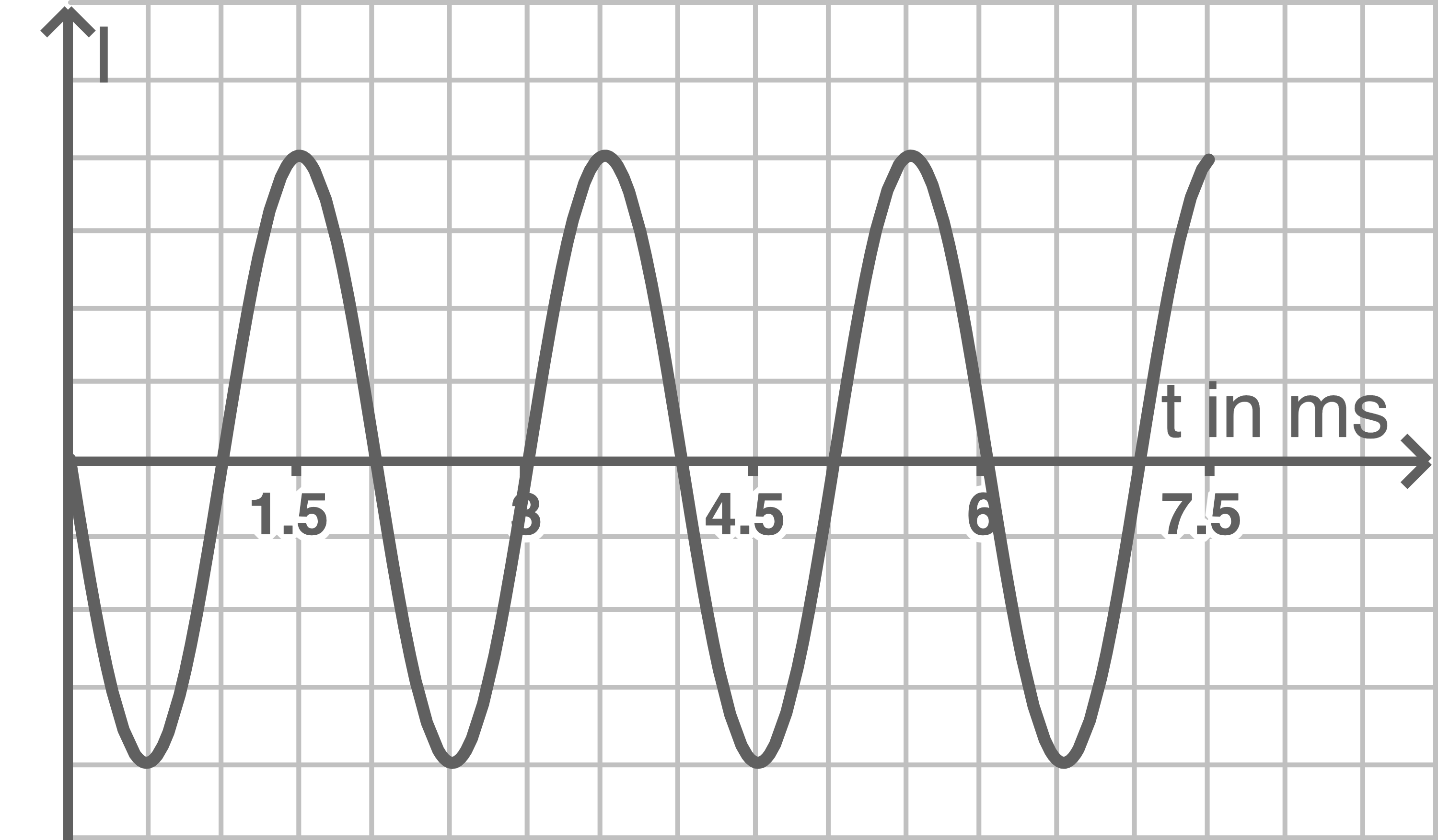

Abbildung 3 a

Abbildung 3 b

Abbildung 3 c

Abbildung 3 d
(7 VP)
3.
Ein homogenes und begrenztes Magnetfeld der Flussdichte  ist senkrecht zur Zeichenebene orientiert. Ein quadratischer Drahtrahmen bewegt sich mit der konstanten Geschwindigkeit
ist senkrecht zur Zeichenebene orientiert. Ein quadratischer Drahtrahmen bewegt sich mit der konstanten Geschwindigkeit  von links nach rechts durch das Magnetfeld (siehe Abbildung). Der Rahmen tritt zum Zeitpunkt
von links nach rechts durch das Magnetfeld (siehe Abbildung). Der Rahmen tritt zum Zeitpunkt  in das Magnetfeld ein.
in das Magnetfeld ein.
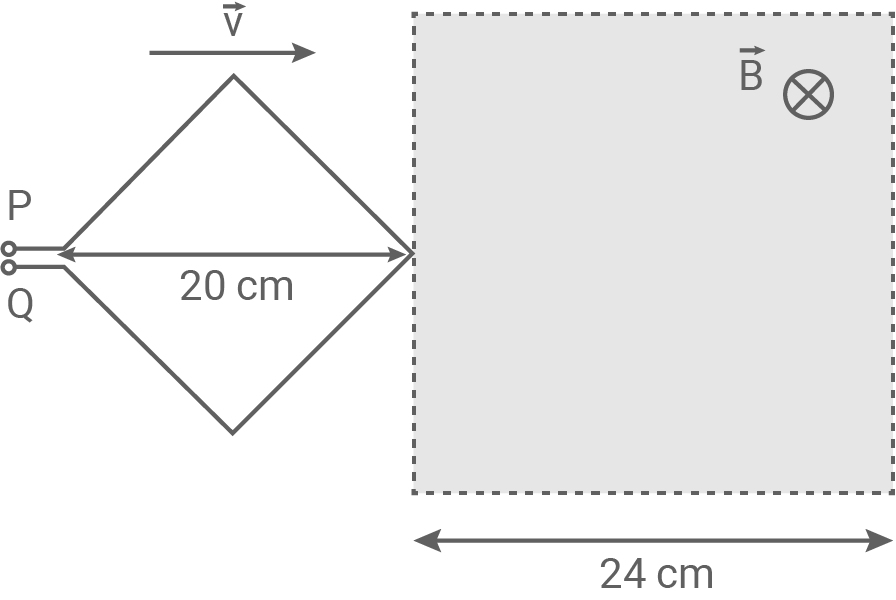
Abbildung 4
a)
Erkläre, weshalb während des Eintauchvorgangs eine Spannung an den Enden des Rahmens auftritt, und gib deren Polung an.
In Abbildung 5 ist der zeitliche Verlauf der Spannung an den Enden des Rahmens dargestellt.
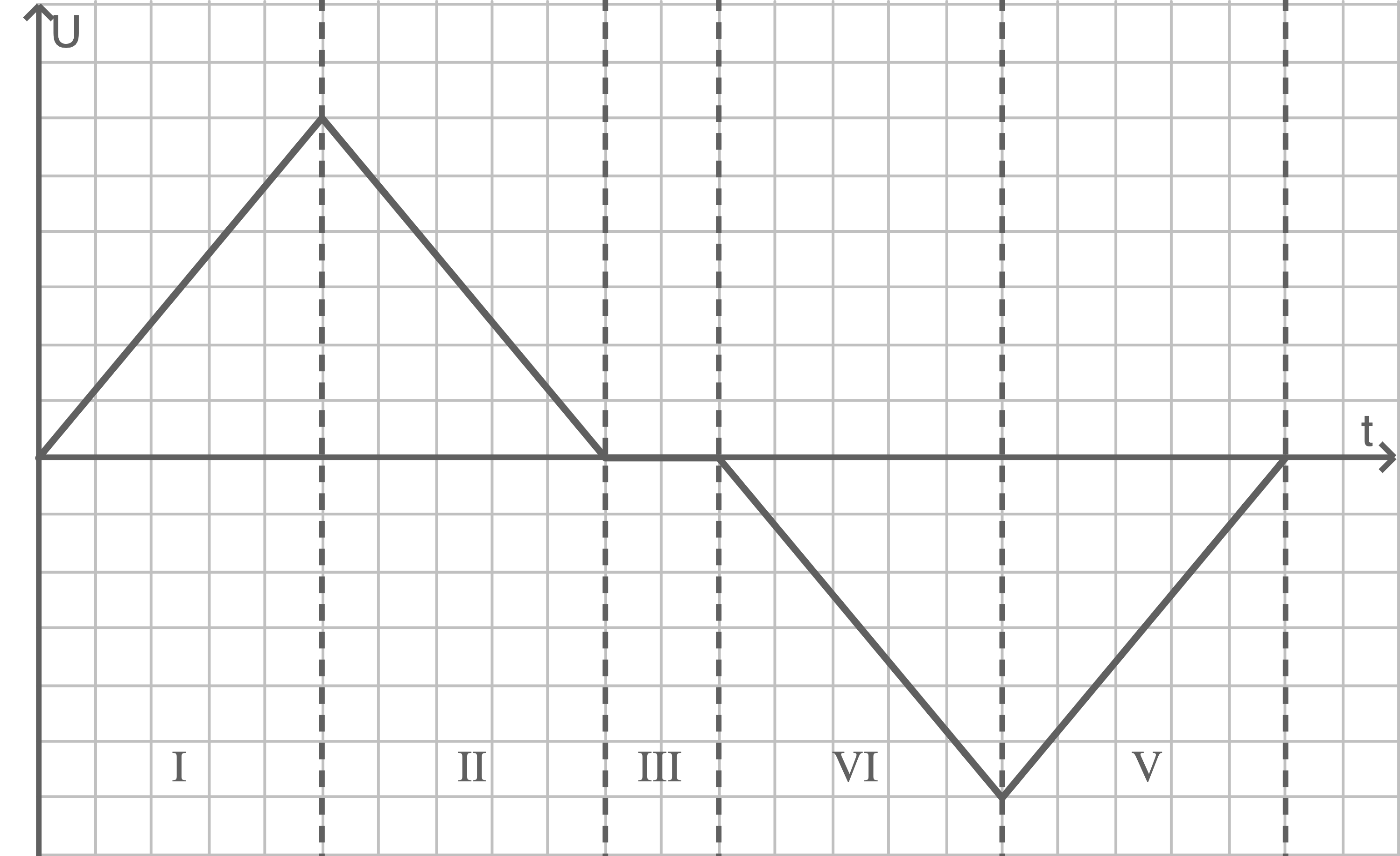
Abbildung 5
b)
Erkläre das Zustandekommen des Spannungsverlaufs in den Bereichen  bis
bis 
c)
Berechne die Zeitpunkte, zu denen der Betrag der induzierten Spannung maximal wird.
d)
Zeige durch eine Rechnung, dass der Wert der maximalen Spannung  beträgt.
beträgt.
Das Experiment wird nun mit doppelter Geschwindigkeit des Rahmens wiederholt.
e)
Zeichne das zugehörige Zeit-Spannung-Diagramm.
(13 VP)
1.
a)
Durch den Drahtbügel fließt Strom und somit wirkt auf ihn eine Lorentzkraft im Magnetfeld. Diese Kraft zeigt in Richtung der Gewichtskraft. Nur die oberen horizentalen Leiterstücke liegen im Magnetfeld und somit wirkt nur auf diese eine Lorentzkraft.
Wird die Stromstärke erhöht, so nimmt auch die Stärke der Lorentzkraft zu und deshalb auch der Wert, der von der Waage angezeigt wird.
b)
Aus der Tabelle ist ersichtlich, dass bei einer Stromstärke von  die Masse der Leiterschleife nicht angezeigt wird (Tara-Funktion der Waage.)
Es gilt:
die Masse der Leiterschleife nicht angezeigt wird (Tara-Funktion der Waage.)
Es gilt: 
 ist die von der Waage angezeigte Masse.
Die magnetische Flussdichte für
ist die von der Waage angezeigte Masse.
Die magnetische Flussdichte für  ergibt sich aus:
ergibt sich aus:



c)
| 0 | 0 | 0 |
| 100 | 2,80 | 27,5 |
| 200 | 5,05 | 49,5 |
| 300 | 7,20 | 70,6 |
| 400 | 10,25 | 101 |
| 500 | 12,30 | 121 |
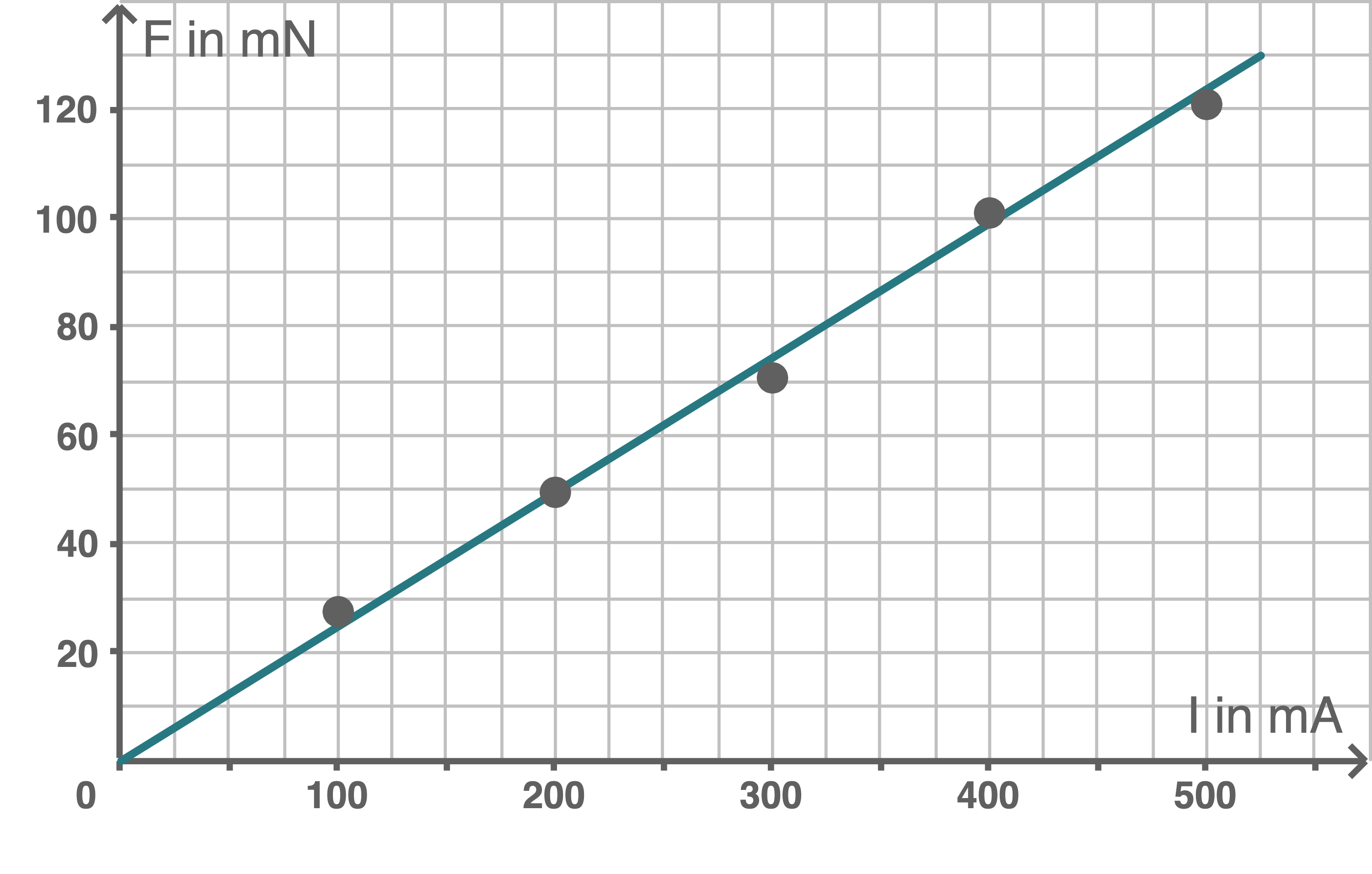
d)
Das Ergebnis aus b) kommt aus nur einer Messung zustande und ist deshalb nicht so genau wie das auc c), denn hier sind alle Messungen in das Ergebnis eingeflossen.
2.
a)
Zunächst liegt am Kondensator die maximale Spannung an. Über die Spule entlädt er sich. Dadurch entsteht in der Spule ein sich änderndes Magnetfeld, wodurch in der Spule eine Spannung entsteht. Durch diese verzögert sich das Anwachsen der Stromstärke.
Ist der Kondensator entladen, so ist die Stromstärke in der Spule maximal. Dadurch nimmt die magnetische Flussdichte in der Spule ab. Durch die induzierte Spannung wird der Kondensator mit umgekehrter Polung wieder aufgeladen. Ist der Kondensator wieder aufgeladen, so wiederholt sich der Vorgang in umgekehrter Richtung.
Wenn am Kondensator die Ausgangsspannung wieder anliegt, so ist eine Schwingungsperiode abgelaufen.
Ist der Kondensator entladen, so ist die Stromstärke in der Spule maximal. Dadurch nimmt die magnetische Flussdichte in der Spule ab. Durch die induzierte Spannung wird der Kondensator mit umgekehrter Polung wieder aufgeladen. Ist der Kondensator wieder aufgeladen, so wiederholt sich der Vorgang in umgekehrter Richtung.
Wenn am Kondensator die Ausgangsspannung wieder anliegt, so ist eine Schwingungsperiode abgelaufen.
b)
Es gilt  und
und  (aus der Abbildung).
Umgeformt ergibt sich für die Induktivität der Spule:
(aus der Abbildung).
Umgeformt ergibt sich für die Induktivität der Spule:


 .
.
c)
Strom- und Spannungsverlauf sind in den Abbildungen 3a und 3b um  verschoben. Der Stromstärkeverlauf muss aber da Nullstellen haben, wo der Spannungsverlauf maximal ist. Somit können 3a und 3b ausgeschlossen werden.
verschoben. Der Stromstärkeverlauf muss aber da Nullstellen haben, wo der Spannungsverlauf maximal ist. Somit können 3a und 3b ausgeschlossen werden.
Bei Abbildung 3d beträgt die Periodendauer
Deshalb ist nur Abbildung 3c geeignet.
Bei Abbildung 3d beträgt die Periodendauer
Deshalb ist nur Abbildung 3c geeignet.
3.
a)
Die magnetische Flussdichte B ist konstant im Feldbereich. Der magnetische Fluss  ändert sich durch das Eintauchen des Rahmens, dadurch wird eine Spannung zwischen den Rahmenenden erzeugt. Die Elektronen, die sich im Feld bewegen, erfahren beim Eintauchen eine Lorentzkraft nach unten (3-Finger-Regel). Dadurch ist das elektrische Potential in Q niedriger als in P.
ändert sich durch das Eintauchen des Rahmens, dadurch wird eine Spannung zwischen den Rahmenenden erzeugt. Die Elektronen, die sich im Feld bewegen, erfahren beim Eintauchen eine Lorentzkraft nach unten (3-Finger-Regel). Dadurch ist das elektrische Potential in Q niedriger als in P.
b)
Bereich I: Die Fläche des Feldes nimmt beim Eintauchvorgang quadratisch mit der Zeit zu. Die induzierte Spannung steigt deshalb in diesem Bereich linear an (Induktionsgesetz.)
Bereich II: Die magnetische Flussänderung sinkt bis zum Zeitpunkt des vollständigen Eintauchens.
Bereich III: Der Rahmen ist nun vollständig im Feld, die induzierte Spannung ist bei konstantem Fluss in dieser Zeitspanne Null.
Bereich VI, V: Wenn der Rahmen das Feld verlässt, kann das gleiche Prinzip wie beim Eintauchen beschrieben werden. Zuerst nimmt die Flussänderung linear zu, danach linear ab. Die induzierte Spannung entspricht der Spannung aus den Bereichen I und II, jedoch ist die Polung vertauscht.
c)
Die Spannung ist maximal, wenn der Rahmen halb eingetaucht ist.


d)
Im ersten Zeitabschnitt gilt für die Änderungsrate der Fläche  Der Maximalwert der induzierten Spannung ergibt sich mit:
Der Maximalwert der induzierten Spannung ergibt sich mit:



e)
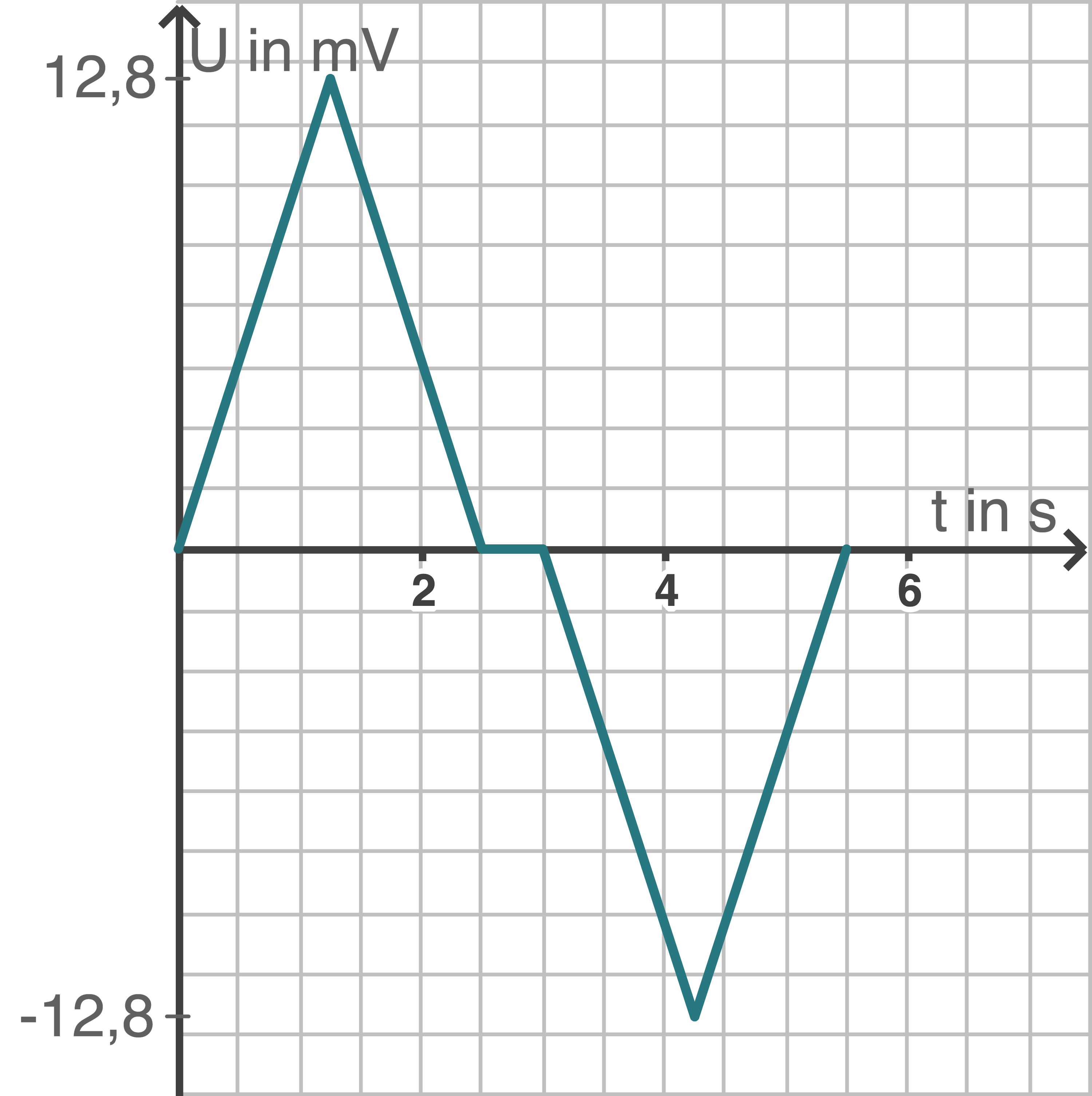 ´
´