Aufgabe 1 – Mechanische Schwingungen
1.
Ein horizontales Federpendel besteht aus einer auf Zug und Druck belastbaren Feder mit der Federkonstanten  und einem daran befestigten Körper der Masse
und einem daran befestigten Körper der Masse  Der Körper wird in
Der Körper wird in  -Richtung um
-Richtung um  aus der Ruhelage nach rechts ausgelenkt und zum Zeitpunkt
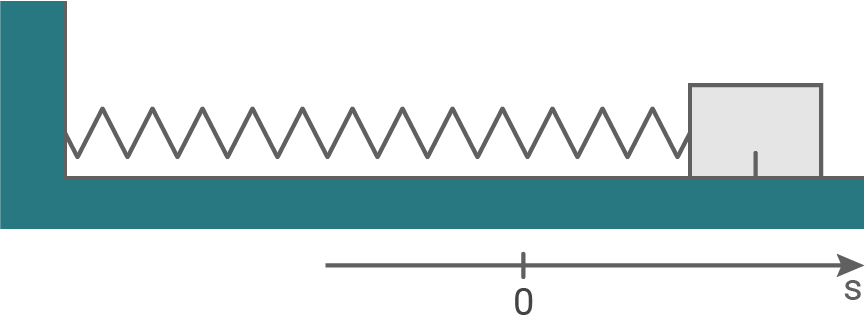
aus der Ruhelage nach rechts ausgelenkt und zum Zeitpunkt  losgelassen (siehe Abbildung 1). Die Masse der Feder bleibt unberücksichtigt und Reibungseffekte werden zunächst vernachlässigt.
losgelassen (siehe Abbildung 1). Die Masse der Feder bleibt unberücksichtigt und Reibungseffekte werden zunächst vernachlässigt.
 sowohl die maximale beschleunigende Kraft als auch die Periodendauer der Schwingung verdoppeln.
sowohl die maximale beschleunigende Kraft als auch die Periodendauer der Schwingung verdoppeln.
 und
und  zweier unmittelbar aufeinander folgender Umkehrpunkte des schwingenden Körpers gilt die Beziehung
zweier unmittelbar aufeinander folgender Umkehrpunkte des schwingenden Körpers gilt die Beziehung  Dabei ist
Dabei ist  die bei der Schwingung wirkende Reibungskraft und
die bei der Schwingung wirkende Reibungskraft und  die Federkonstante.
die Federkonstante.

Abbildung 1
a)
Zeige, dass die Periodendauer der Schwingung  beträgt.
beträgt.
b)
Bestimme den Ort des schwingenden Körpers zum Zeitpunkt 
Die Anordnung soll nun so verändert werden, dass sich bei der Amplitude von
c)
Erläutere die hierzu nötigen Veränderungen im Versuchsaufbau.
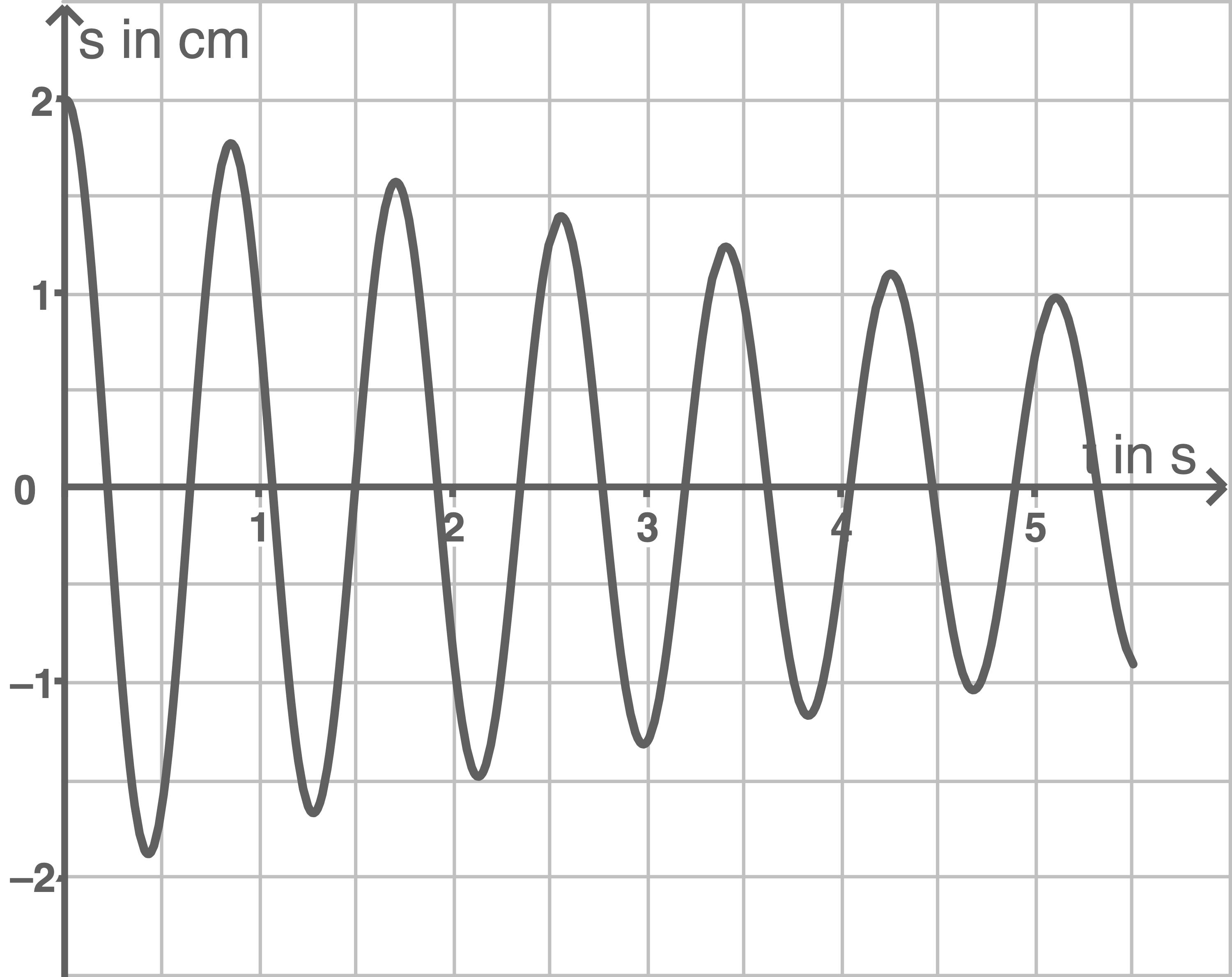
Nun wird wieder die anfängliche Anordnung betrachtet. Tatsächlich ist die Schwingung so gedämpft, dass die Amplitude linear abnimmt. Abbildung 2 zeigt das zugehörige Zeit-Auslenkung-Diagramm.

Abbildung 2
d)
Bestimme, wie viel Prozent der anfänglichen Energie nach den ersten sechs Perioden noch im Federpendel enthalten ist.
e)
Bestimme möglichst genau die Abnahme der Amplitude pro Schwingungsperiode.
Für die Auslenkungen
f)
Bestimme den Betrag der Reibungskraft.
(12 VP)
2.
In einem Experiment mit einem elektromagnetischen Schwingkreis wird die Spannung am Kondensator in Abhängigkeit von der Zeit gemessen (siehe Abbildung 3).
 Im Folgenden werden ungedämpfte Schwingungen betrachtet.
Im Folgenden werden ungedämpfte Schwingungen betrachtet.

 haben. Es stehen dafür drei Kondensatoren mit
haben. Es stehen dafür drei Kondensatoren mit 
 und
und  und eine Spule mit kontinuierlich veränderlicher Induktivität im Bereich von
und eine Spule mit kontinuierlich veränderlicher Induktivität im Bereich von  bis
bis  zur Verfügung.
zur Verfügung.
a)
Zeichne einen möglichen Schaltplan für dieses Experiment und beschreibe dessen Durchführung.
b)
Begründe, warum die Amplitude der Spannung mit der Zeit abnimmt.

Abbildung 3
c)
Leite die Differenzialgleichung  für die zeitliche Änderung der elektrischen Ladung eines elektromagnetischen Schwingkreises her.
für die zeitliche Änderung der elektrischen Ladung eines elektromagnetischen Schwingkreises her.
Die Differenzialgleichung für die zeitliche Änderung der Auslenkung eines Federpendels lautet:
d)
Vergleiche die beiden Differenzialgleichungen hinsichtlich ihrer mathematischen Struktur und gib sich entsprechende Größen an.
Ein elektromagnetischer Schwingkreis soll eine Periodendauer von
e)
Bestimme ein passendes Wertepaar aus Kapazität und Induktivität.
(11 VP)
3.
Bei der Darstellung von geradlinigen Bewegungen werden häufig Diagramme erstellt, die den funktionalen Zusammenhang zwischen unterschiedlichen physikalischen Größen zeigen.
Beurteile für jedes der Diagramme aus Abbildung 4, ob es zu einer harmonischen Schwingung gehören kann.
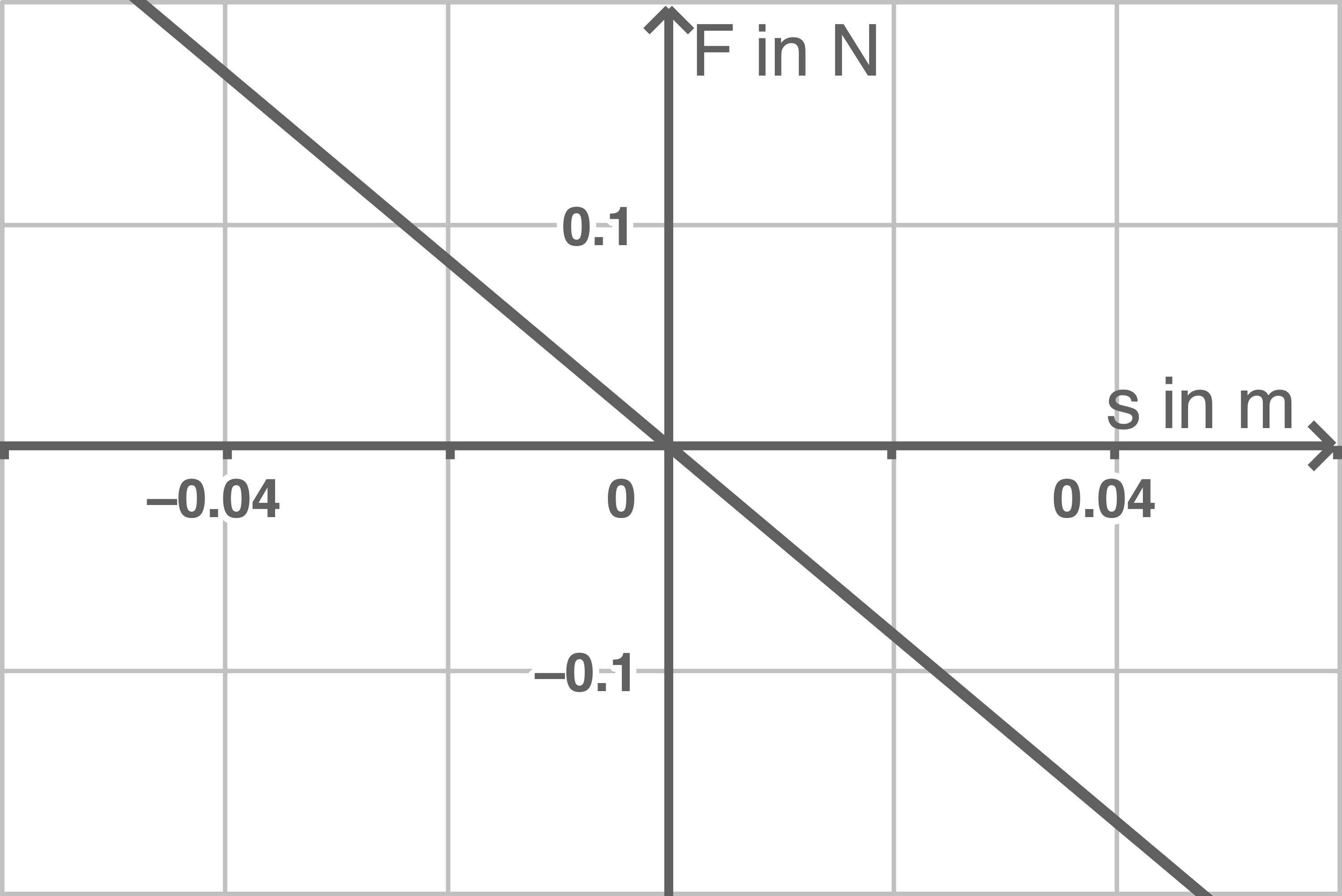
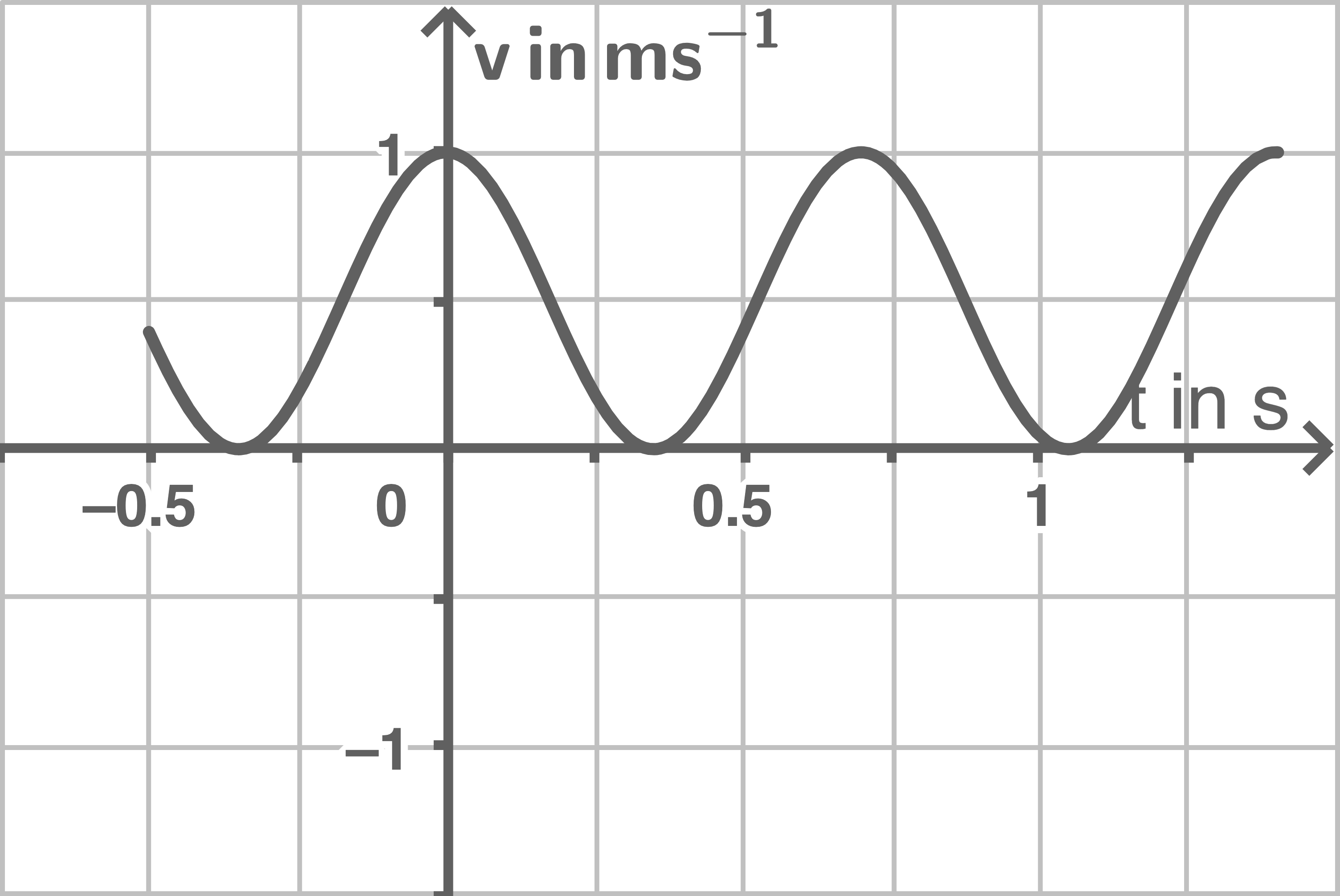
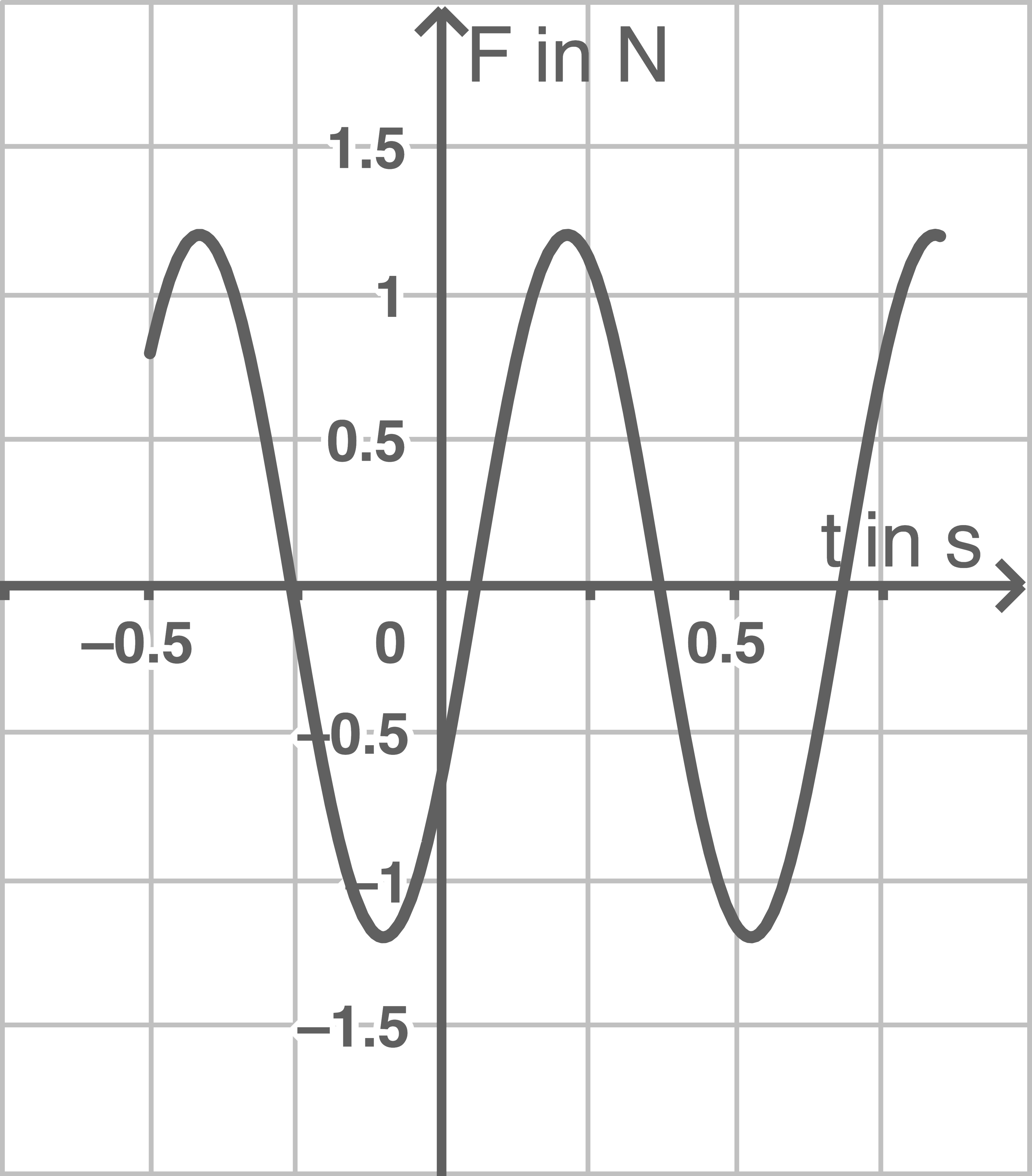
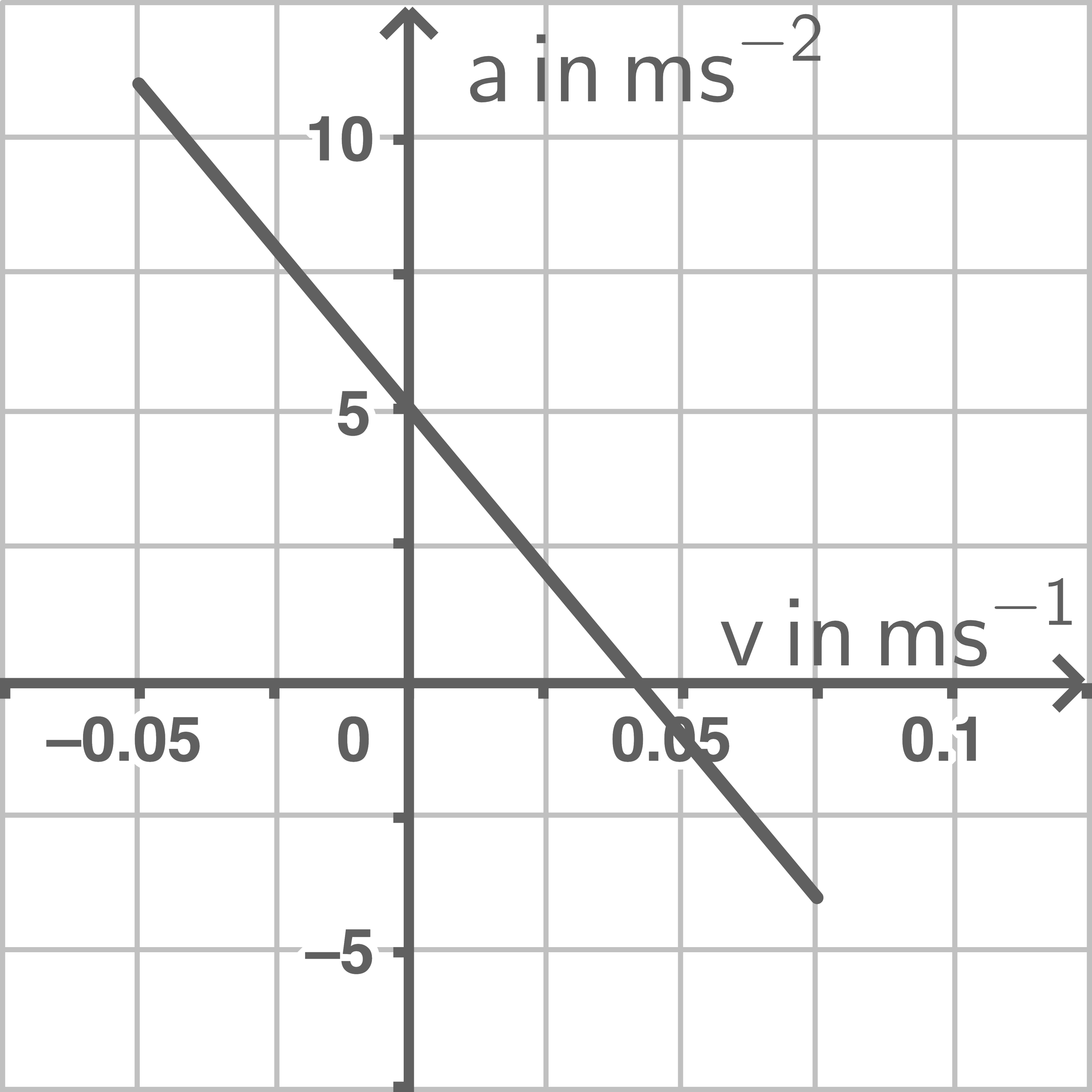
Beurteile für jedes der Diagramme aus Abbildung 4, ob es zu einer harmonischen Schwingung gehören kann.

Abbildung 4a

Abbildung 4b

Abbildung 4c

Abbildung 4d
(7 VP)
1.
a)
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
T &=& 2\pi\cdot\sqrt{\dfrac{m}{D}} \\[5pt]
T &=& 2\pi\cdot\sqrt{\dfrac{0,250\,\mathrm{~kg}}{13,9\,\mathrm{~Nm}^{-1}}} \\[5pt]
T &=& 0,84\,\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/01b6c6c4ae1fb647f70d7c60ffee82a3c1de74314c33549d040a73a77f21df1f_light.svg)
b)
Gegeben:
 Gesucht:
Gesucht:  Lösung:
Lösung:
 Es gilt
Es gilt  und somit:
und somit:

 Nach 0,5 Sekunden hat sich der Körper um ca. 1,7 cm nach links ausgehend von der Ruhelage bewegt.
Nach 0,5 Sekunden hat sich der Körper um ca. 1,7 cm nach links ausgehend von der Ruhelage bewegt.
c)
1. Schritt: Formeln von denen das Federpendel abhängt
Die Kraft, die auf den Körper einwirkt, ist gegeben durch:  . Aus dieser Formel kann die Formel für die maximale Kraft
. Aus dieser Formel kann die Formel für die maximale Kraft  , die auf den Körper einwirkt, gefolgert werden. Diese ist
, die auf den Körper einwirkt, gefolgert werden. Diese ist  . Die Formel für die Periodendauer ist schon in der Teilaufgabe a) gegeben.
2. Schritt: Veränderung der Formeln durch veränderte Anordnung
Es gilt
. Die Formel für die Periodendauer ist schon in der Teilaufgabe a) gegeben.
2. Schritt: Veränderung der Formeln durch veränderte Anordnung
Es gilt  . Nach Aufgabenstellung soll
. Nach Aufgabenstellung soll  konstant bleiben. Daraus folgt bei Verdoppelung von
konstant bleiben. Daraus folgt bei Verdoppelung von  dass sich auch
dass sich auch  verdoppeln muss. Es muss eine neue Feder mit
verdoppeln muss. Es muss eine neue Feder mit  gewählt werden.
Für die neue Periodendauer der Schwingung gilt mit
gewählt werden.
Für die neue Periodendauer der Schwingung gilt mit  :
:
![\(\begin{array}[t]{rll}
T](https://www.schullv.de/resources/formulas/f1e0953c233e87c2887c0dc263b65a27ed7632eff9f2e5f8001e2e0c0a47f3db_light.svg) Wird die Masse des Pendelkörpers auf den achtfachen Betrag erhöht, so verdoppelt sich die Schwinungsdauer. Hierbei beträgt die Periodendauer dann
Wird die Masse des Pendelkörpers auf den achtfachen Betrag erhöht, so verdoppelt sich die Schwinungsdauer. Hierbei beträgt die Periodendauer dann 
d)
Die Formel der Spannenergie ist gegeben durch  . Aus dem Diagramm kann abgelesen werden, dass sich die maximale Auslenkung nach 6 Perioden auf
. Aus dem Diagramm kann abgelesen werden, dass sich die maximale Auslenkung nach 6 Perioden auf  halbiert hat. Also ist
halbiert hat. Also ist  Die Federkonstante bleibt laut Aufgabenstellung gleich. Damit verändert sich auch die im System befindliche Energie. Für das Verhältnis der beiden Energien ergibt sich folgendes:
Die Federkonstante bleibt laut Aufgabenstellung gleich. Damit verändert sich auch die im System befindliche Energie. Für das Verhältnis der beiden Energien ergibt sich folgendes:





 Die noch im System befindliche Energie beträgt nur noch
Die noch im System befindliche Energie beträgt nur noch  der anfänglichen Energie.
der anfänglichen Energie.
e)
In den ersten sechs Perioden nimmt die Amplitude um  ab. Da die Abnahme nach Aufgabenstellung linear verläuft ist sie bei jeder Schwingungsperiode gleich. Die Abnahme pro Periode beträgt also
ab. Da die Abnahme nach Aufgabenstellung linear verläuft ist sie bei jeder Schwingungsperiode gleich. Die Abnahme pro Periode beträgt also 
 .
.
f)
2.
a)
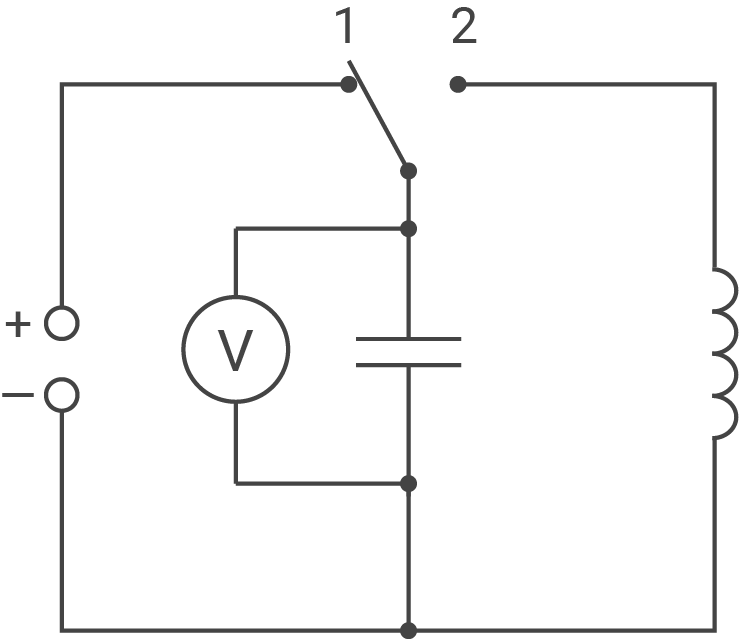
b)
Aufgrund des ohmische Widerstands der Spule und der Kabel wird ein Teil der Energie des Schwingkreises in thermische Energie (Wärme) umgewandelt.
c)
Herleitung der Differenzialgleichung
 ist die Spannung an der Spule in Abhänigkeit der Zeit.
ist die Spannung an der Spule in Abhänigkeit der Zeit.  ist die Spannung am Kondensator in Abhänigkeit der Zeit. Da keine Spannungsquelle anliegt ist die Spannung des Schwingkreises gleich null. Somit gilt:
ist die Spannung am Kondensator in Abhänigkeit der Zeit. Da keine Spannungsquelle anliegt ist die Spannung des Schwingkreises gleich null. Somit gilt:  Für die Spannung
Für die Spannung  an der Spule gilt:
an der Spule gilt:  .
Für die Spannung
.
Für die Spannung  an dem Kondensator gilt:
an dem Kondensator gilt:  .
Einsetzen ergibt:
.
Einsetzen ergibt:
d)
Auflösen der Differenzialgleichung nach null:
![\(\begin{array}[t]{rll}
\ddot{Q}(t) &=& - \dfrac{1}{L \cdot C} \cdot Q(t) &\quad \scriptsize \mid\; - \ddot{Q}(t) \\[5pt]
0 &=& - \dfrac{1}{L \cdot C} \cdot Q(t) - \ddot{Q}(t) &\quad \scriptsize \mid\; \cdot (- L) \\[5pt]
0 &=& \dfrac{Q(t)}{C} + L\cdot\ddot{Q}(t) \\[5pt]
0 &=& L\cdot\ddot{Q}(t)+\dfrac{Q(t)}{C}
\end{array}\)](https://www.schullv.de/resources/formulas/c22b4b0c48332fe037444f2134c42e726eae49c5c086e55e640b175bcc86c026_light.svg) Die beiden Gleichungen
Die beiden Gleichungen  und
und  sind bzgl. ihrer mathematischen Struktur in Vorzeichen und Form identisch.
sind bzgl. ihrer mathematischen Struktur in Vorzeichen und Form identisch.
Die Masse entspricht der Eigeninduktivität
entspricht der Eigeninduktivität  . Die Federkonstante
. Die Federkonstante  entspricht dem Kehrwert der Kapazität
entspricht dem Kehrwert der Kapazität 
Die Masse
e)
Durch Probieren stellt sich heraus, dass sich die Periodendauer nur mit einer Kapazität von
Aus
3.
Wenn der Betrag der rücktreibenden Kraft proportional zur Auslenkung ist, dann ist eine Schwingung harmonisch.
- Beurteilung Schaubild 4a: Wenn
beschleunigende Kraft und als rücktreibende Kraft proportional zur Auslenkung
ist, kann das Schaubild zu einer harmonischen Schwingung gehören.
- Beurteilung Schaubild 4b: Hierbei kann es sich nicht um eine harmonische Schwingung handeln, da die Geschwindigkeit keine negative Werte annehmen kann und der Körper sich somit nur in eine Richtung bewegt.
- Beurteilung Schaubild 4c: Das Schaubild kann zu einer harmonischen Schwingung gehören. Hierbei gilt
. Weil
gilt Entsprechendes für
.
- Beurteilung Schaubild 4d: Das Schaubild passt nicht zu einer harmonischen Schwingung, weil ein harmonisch schwingender Körper in seinem Umkehrpunkt seiner Bewegung die Geschwindigkeit
hat und dies hier nicht vorliegt.