Aufgabe 4 – Elektromagnetismus
1.
Die kreisförmigen Platten eines Kondensators besitzen einen Radius von 
und haben einen Abstand von 
Der Raum zwischen den Platten ist mit einem der in Tabelle 1 genannten Dielektrika vollständig ausgefüllt.
Tabelle 1
In einer Messreihe wird der Kondensator mit verschiedenen Spannungen 
aufgeladen. Für jede Spannung wird die auf dem Kondensator befindliche Ladung 
gemessen. Tabelle 2 zeigt die zugehörigen Messwerte:
Tabelle 2
Die obige Messung wird mit den gleichen Spannungswerten wiederholt.
und haben einen Abstand von Der Raum zwischen den Platten ist mit einem der in Tabelle 1 genannten Dielektrika vollständig ausgefüllt.
| Dielektrikum | relative Permittivität |
|---|---|
| Gummi | 3,5 |
| Glas | 10 |
| Polystyrol | 2,5 |
aufgeladen. Für jede Spannung wird die auf dem Kondensator befindliche Ladung gemessen. Tabelle 2 zeigt die zugehörigen Messwerte:
 in  |
 in  |
|---|---|
| 0,5 | 83,0 |
| 1,0 | 168 |
| 2,0 | 325 |
| 3,0 | 510 |
| 4,0 | 655 |
a)
Stelle die Ladung in Abhängigkeit von der Spannung in einem geeigneten Schaubild dar und begründe den Kurvenverlauf.
in Abhängigkeit von der Spannung in einem geeigneten Schaubild dar und begründe den Kurvenverlauf.
b)
Ermittle unter Verwendung aller Messwerte die Kapazität des mit dem Dielektrikum gefüllten Kondensators.
c)
Bestimme das verwendete Dielektrikum.
In einem neuen Versuch ist der Kondensator vollständig mit Glas gefüllt. Der Abstand der Kondensatorplatten beträgt nun Die obige Messung wird mit den gleichen Spannungswerten wiederholt.
d)
Ermittle, wie sich die Ladungen auf den Platten gegenüber Tabelle 2 verändern.
e)
Erläutere, weshalb ein Dielektrikum die Kapazität eines Kondensators erhöht.
(11 VP)
2.
Ein elektromagnetischer Schwingkreis besteht aus einer Spule mit einer Induktivität 
von 
und einem Kondensator mit veränderbarer Kapazität 
Für den zeitlichen Verlauf der Ladung auf dem Kondensator gilt die Differenzialgleichung:
bis 
ausgelegt werden.
eingestellt, die Maximalspannung im Schwingkreis hat den Wert 
Berechne die maximale Stromstärke in diesem Schwingkreis.
von und einem Kondensator mit veränderbarer Kapazität Für den zeitlichen Verlauf der Ladung auf dem Kondensator gilt die Differenzialgleichung:
a)
Leite aus der Differenzialgleichung eine Formel für die Frequenz des Schwingkreises in Abhängigkeit von und 
her.
Der Schwingkreis soll für den Bereich von und her.
bis ausgelegt werden.
b)
Bestimme den Kapazitätsbereich des regelbaren Kondensators, sodass man den kompletten Frequenzbereich abdecken kann.
Die Kapazität des Kondensators wird auf eingestellt, die Maximalspannung im Schwingkreis hat den Wert
c)
(8 VP)
3.
Mithilfe einer Spannung 
werden Elektronen mit vernachlässigbarer Anfangsgeschwindigkeit beschleunigt. Sie verlassen den Beschleuniger in waagrechter Richtung und treten anschließend in das elektrische Feld des Kondensators 1 ein (siehe Abb. 1). Der Raum zwischen seinen Platten, die einen Abstand von 
haben, wird zusätzlich von einem homogenen Magnetfeld durchsetzt, dessen Feldlinien senkrecht in die Zeichenebene hineingerichtet sind.
Elektronen, die die Öffnung
passieren, gelangen anschließend in den Kondensator 2, dessen Plattenabstand ebenfalls beträgt. Die gesamte Anordnung ist evakuiert. Zunächst werden die Elektronen mit einer Spannung von 
beschleunigt.
werden Elektronen mit vernachlässigbarer Anfangsgeschwindigkeit beschleunigt. Sie verlassen den Beschleuniger in waagrechter Richtung und treten anschließend in das elektrische Feld des Kondensators 1 ein (siehe Abb. 1). Der Raum zwischen seinen Platten, die einen Abstand von haben, wird zusätzlich von einem homogenen Magnetfeld durchsetzt, dessen Feldlinien senkrecht in die Zeichenebene hineingerichtet sind.
Elektronen, die die Öffnung
passieren, gelangen anschließend in den Kondensator 2, dessen Plattenabstand ebenfalls beträgt. Die gesamte Anordnung ist evakuiert. Zunächst werden die Elektronen mit einer Spannung von beschleunigt.
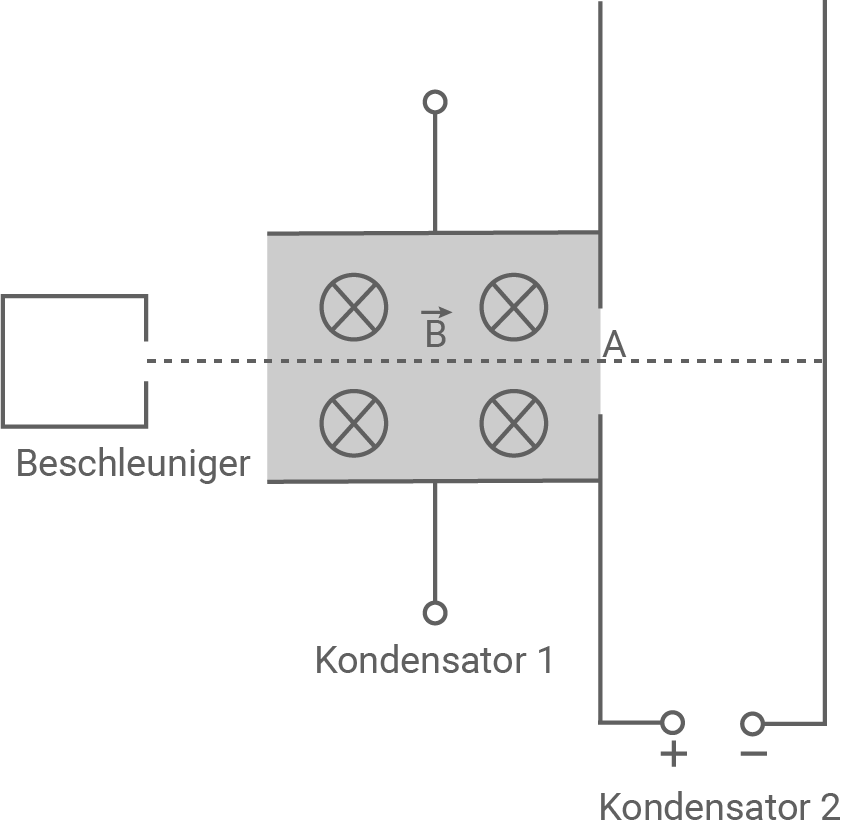
Abbildung 1
a)
Zeige, dass die Elektronen den Beschleuniger mit einer Geschwindigkeit von 
verlassen.
Die Spannung zwischen den Kondensatorplatten des Kondensators 1 beträgt verlassen.
b)
Bestimme die Richtung des elektrischen Feldes und den Betrag der magnetischen Flussdichte, sodass die Elektronen den Kondensator 1 geradlinig durchlaufen.
Anschließend treten die Elektronen im Punkt in das Feld des Kondensators 2 ein. Durch Anlegen einer geeigneten Spannung zwischen seinen Kondensatorplatten lassen sich die Elektronen im Feldbereich bis auf die Geschwindigkeit 
abbremsen. Die im Feldbereich bis dahin zurückgelegte Strecke nennt man Eindringtiefe.
c)
Bestimme die Mindestspannung, die man benötigt, damit die Elektronen die rechte Platte des Kondensators 2 gerade nicht erreichen.
d)
Zeichne ein Diagramm, das die Eindringtiefe der Elektronen in den Kondensator 2 in Abhängigkeit von der angelegten Spannung im Bereich von 
bis 
darstellt.
Die Elektronen werden im Feldbereich des Kondensators 2 abgestoppt und erreichen anschließend wieder den Punkt bis darstellt.
Die Polung am Kondensator 1 bleibt unverändert.
e)
Begründe, ob die weitere Bewegung der Elektronen im Kondensator 1 geradlinig verläuft.
(11 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die Messwerte werden als Punkte in einem Koordinatensystem dargestellt und es wird eine ausgleichende Ursprungsgerade eingezeichnet.
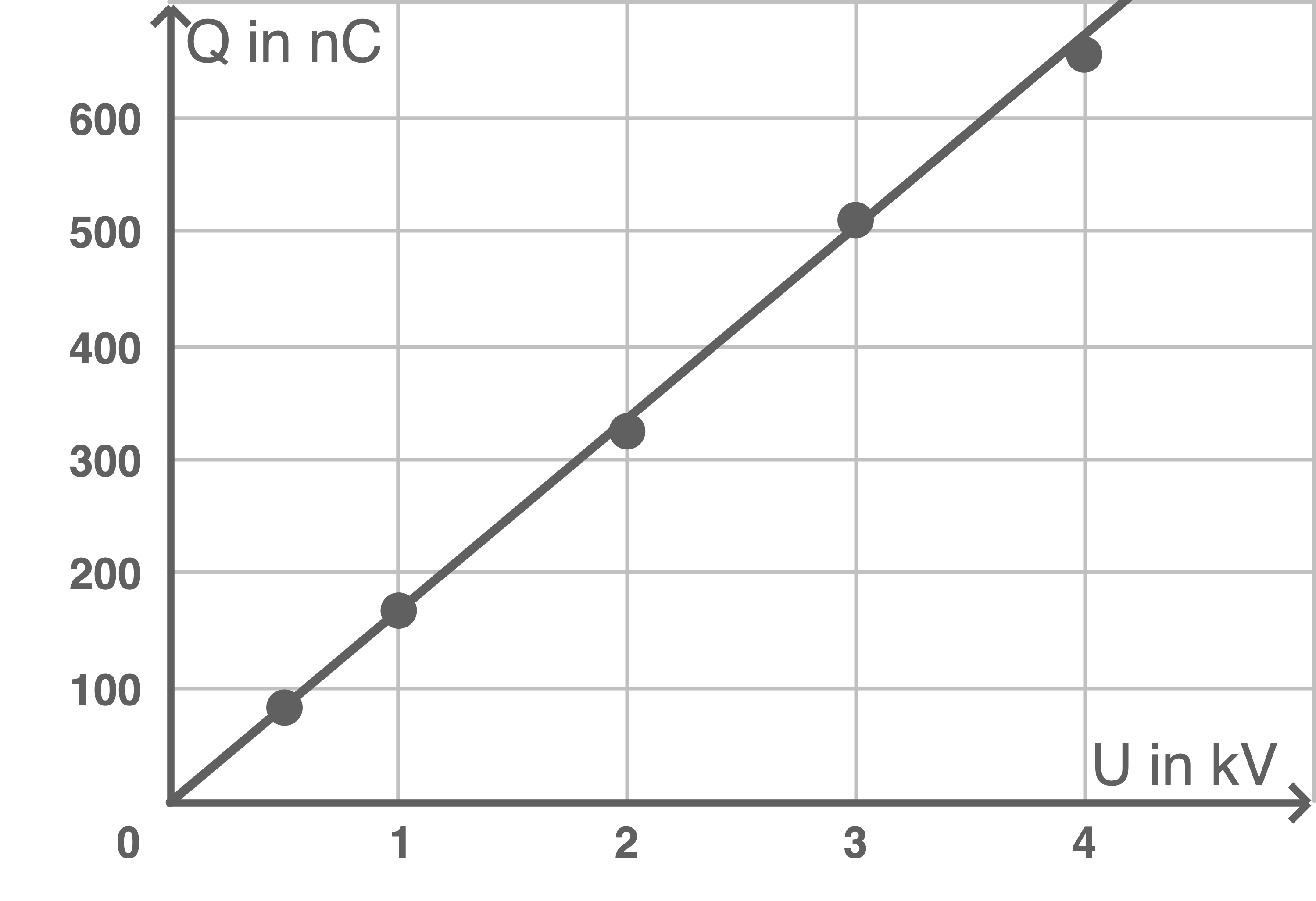Es gilt 
wobei 
proportional zu ist, dies stellt die Gerade dar. Die Punkte weichen minimal von der Geraden ab, bedingt durch Messungenauigkeiten.
U-Q-Diagramm
wobei proportional zu ist, dies stellt die Gerade dar. Die Punkte weichen minimal von der Geraden ab, bedingt durch Messungenauigkeiten.
b)
Es gilt 
und somit folgt für die Messwerte:
Die Kapazität des mit dem Dielektrium gefüllten Kondensators entspricht dem Mittelwert mit 
und somit folgt für die Messwerte:
| in kV |
 in nC |
 in  F |
|---|---|---|
| 0,5 | 83,0 | 0,166 |
| 1,0 | 168 | 0,168 |
| 2,0 | 325 | 0,163 |
| 3,0 | 510 | 0,170 |
| 4,0 | 655 | 0,164 |
c)
Es gilt:
Der Kondensator ist mit Polystyrol gefüllt.
![\(\begin{array}[t]{rll}
C&=& \varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{A}{d} &\quad \scriptsize \mid\;\cdot \dfrac{d}{A} \quad \mid\;:\varepsilon_0\\[5pt]
\dfrac{C\cdot d}{\varepsilon_0\cdot A}&=&\varepsilon_r &\quad \scriptsize \\[5pt]
\varepsilon_r&=& \dfrac{C\cdot d}{\varepsilon_0\cdot A} &\quad \scriptsize \\[5pt]
\varepsilon_r&=& \dfrac{ 0,166 \cdot 10^{-9} \cdot 0,0030}{8,85 \cdot 10^{-12}\cdot \pi \cdot 0,085^2} &\quad \scriptsize \\[5pt]
\varepsilon_r&=& 2,5
\end{array}\)](https://www.schullv.de/resources/formulas/b01af0b0f9b2600fec121298d06c5ac9c59b60bf98fbde87aa9f808a6f0f3d9e_light.svg)
d)
Aus 
und folgt:
![\(\begin{array}[t]{rll}
\dfrac{Q}{U}&=&\varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{A}{d} &\quad \scriptsize \mid\; \cdot U\\[5pt]
Q&=&\varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{A}{d} \cdot U
\end{array}\)](https://www.schullv.de/resources/formulas/879ea5e5e5b7e2561e85564f9d452847c4abafbf0ab42c3fb2c54187027c3ef9_light.svg)
Durch die Verdopplung des Plattenabstandes folgt: 
Da Polystyrol durch Glas ersetzt wird, folgt 
Die Ladungen der Platten verdoppeln sich.
und folgt:
Durch die Verdopplung des Plattenabstandes folgt:
Da Polystyrol durch Glas ersetzt wird, folgt
Die Ladungen der Platten verdoppeln sich.
![\(\begin{array}[t]{rll}
Q*&=&\varepsilon_0 \cdot \varepsilon_r* \cdot \dfrac{A}{d*} \cdot U &\quad \scriptsize \\[5pt]
&=& \varepsilon_0 \cdot 4 \varepsilon_r \cdot \dfrac{A}{2\cdot d} \cdot U &\quad \scriptsize \\[5pt]
&=& \varepsilon_0 \cdot \dfrac{4}{2}\cdot \varepsilon_r \cdot \dfrac{A}{ d} \cdot U &\quad \scriptsize \\[5pt]
&=& 2 \cdot \varepsilon_0 \cdot \varepsilon_r \cdot \dfrac{A}{ d} \cdot U &\quad \scriptsize \\[5pt]
&=& 2\cdot Q
\end{array}\)](https://www.schullv.de/resources/formulas/ca834fa980842c274ac9bda749af2ea7a66dd8ff58f291cdeeac1f8a7aa2d95b_light.svg)
e)
Im Dielektrikum entsteht ein elektrisches Feld, wenn das Dielektrikum in einen von der Spannungsquelle getrennten Kondensator eingeführt wird. Dieses elektrische Feld ist dem äußeren Feld des Kondensators entgegengerichtet.
Durch die Überlagerung beider Felder sinkt die elektrische Feldstärke, außerdem kann die Ladung der Platten sich nicht ändern, da der Kondensator nicht mit der Stromquelle verbunden ist.
Somit steigt die Kapazität durch die sinkende Feldstärke.
Somit steigt die Kapazität durch die sinkende Feldstärke.
2
a)
Die Differenzialgleichung hat Lösungen der Form 
1. Schritt: Ableitungen bilden
![\(\begin{array}[t]{rll}
\dot{Q}(t)&=&Q_{\text{max}}\cdot \omega\cdot \cos(\omega t +\varphi) \\[5pt]
\ddot{Q}(t)&=& -Q_{\text{max}}\cdot \omega^2 \cdot \sin(\omega t +\varphi) \\[5pt]
&=&-\omega^2 \cdot Q(t)
\end{array}\)](https://www.schullv.de/resources/formulas/4109a329331e535506564db72a2e849609c1640921195cd12942b5c67ec6d268_light.svg)
2. Schritt: Gleichsetzen mit der gegebenen Differenzialgleichung
![\(\begin{array}[t]{rll}
-\omega^2 \cdot Q(t)&=& -\dfrac{1}{L\cdot C}\cdot Q(t) \\[5pt]
\omega^2&=&\dfrac{1}{L\cdot C}
\end{array}\)](https://www.schullv.de/resources/formulas/cbfbeb83237feeb88c005a4c8173adcaea7db45101cd36b1b56a96a8ef4ac62a_light.svg)
Mit 
folgt:
![\(\begin{array}[t]{rll}
(2\pi \cdot f)^2&=&\dfrac{1}{L\cdot C} &\quad \scriptsize \mid\;\sqrt{\quad} \\[5pt]
2\pi \cdot f &=& \dfrac{1}{ \sqrt{L\cdot C}} &\quad \scriptsize \mid\; :2\pi \\[5pt]
f&=& \dfrac{1}{ 2 \pi \cdot \sqrt{L\cdot C}}
\end{array}\)](https://www.schullv.de/resources/formulas/6b8502ed586ba82f719fe1edee60857a3957dde48dedd1ea9984b3e39a8402b6_light.svg)
1. Schritt: Ableitungen bilden
2. Schritt: Gleichsetzen mit der gegebenen Differenzialgleichung
Mit folgt:
b)
Die Kapazität folgt aus:
![\(\begin{array}[t]{rll}
f&=& \dfrac{1}{ 2 \pi \cdot \sqrt{L\cdot C}} &\quad \scriptsize \mid\;(\;)^2 \\[5pt]
f^2&=& \dfrac{1}{ 4 \pi^2 \cdot L\cdot C} &\quad \scriptsize \mid\;\cdot C \; \mid\;:f \\[5pt]
C &=& \dfrac{1}{4 \pi^2 \cdot L\cdot f^2}
\end{array}\)](https://www.schullv.de/resources/formulas/61e8662504b5bdad8d8d0a2de5f531821f0c6d5a0ca886fddf12008a37853e1a_light.svg)
Für 
und 
folgen die minimale und die maximale Kapazität des Kapazitätsbereiches:
![\(\begin{array}[t]{rll}
C_{\text{min}}&=& \dfrac{1}{4 \pi^2 \cdot L\cdot f_{\text{max}}^2} \\[5pt]
&=& \dfrac{1}{4 \pi^2 \cdot L\cdot (2,48\cdot 10^{-9})^2} F \\[5pt]
&=&2,42\cdot 10^{-12}\; \text{F}
\end{array}\)](https://www.schullv.de/resources/formulas/d35cca29b53c7bd770b6f7e21757d0a130ef8431275ac7921b641b836b1c3775_light.svg)
![\(\begin{array}[t]{rll}
C_{\text{max}}&=& \dfrac{1}{4 \pi^2 \cdot L\cdot f_{\text{min}}^2} \\[5pt]
&=& \dfrac{1}{4 \pi^2 \cdot L\cdot (2,40\cdot 10^{-9})^2} F \\[5pt]
&=& 2,59\cdot 10^{-12}\; \text{F}
\end{array}\)](https://www.schullv.de/resources/formulas/3cac7fea3f38b2b7c3aadfcc2d14e2e09b76506e0aa3173218d75f91154cf202_light.svg)
Kapazitäten zwischen 
und 
decken den kompletten Frequenzbereich ab.
folgt aus:
Für und folgen die minimale und die maximale Kapazität des Kapazitätsbereiches:
Kapazitäten zwischen und decken den kompletten Frequenzbereich ab.
c)
Zu Beginn ist der Kondensator geladen, bis die Energie vollständig im Kondensator gespeichert ist. Anschließend wird die Energie näherungsweise vollständig an die Spule abgegeben. Dementsprechend ist die maximale magnetische Energie 
gleich der maximalen elektrischen Energie 
Aus der Energieerhaltung folgt:
gleich der maximalen elektrischen Energie
Aus der Energieerhaltung folgt:
![\(\begin{array}[t]{rll}
\dfrac{1}{2}\cdot L\cdot I_{\text{max}}^2&=& \dfrac{1}{2}\cdot C\cdot U_{\text{max}}^2 \\[5pt]
L\cdot I_{\text{max}}^2&=& C\cdot U_{\text{max}}^2 &\quad \scriptsize \mid\;:L \\[5pt]
I_{\text{max}}^2 &=& \dfrac{C}{L}\cdot U_{\text{max}}^2 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
I_{\text{max}}&=& \sqrt{\dfrac{2,50 \cdot 10^{-12}}{1,70 \cdot 10^{-9}}}\cdot 10,0 \;\text{A} &\quad \scriptsize \\[5pt]
&=& 0,383\;\text{A}
\end{array}\)](https://www.schullv.de/resources/formulas/be969a1997f77bc96d38884edfe9759399216f805f5166012e25d173aea66625_light.svg)
3
a)
Aus der Energieerhaltung folgt:
![\(\begin{array}[t]{rll}
E_{kin} & = & E_{el} &\quad \scriptsize \\[5pt]
\dfrac{mv^2}{2} &=& U\cdot q &\quad \scriptsize \mid \, q=e \\[5pt]
\dfrac{mv^2}{2} &=& U\cdot e &\quad \scriptsize \mid\, \cdot 2\\[5pt]
m \cdot v^2 &=& 2\cdot U \cdot e &\quad \scriptsize \mid \, :m\\[5pt]
v^2 &=& \dfrac{2\cdot U \cdot e}{m} &\quad \scriptsize \mid \, \sqrt{\quad} \\[5pt]
v&=& \sqrt{\dfrac{2\cdot U \cdot e}{m}} &\quad \scriptsize \\[5pt]
v&=& \sqrt{\dfrac{2\cdot 100 \text{V} \cdot 1,60\cdot 10^{-19}\text{C}}{9,11\cdot10^{-31}\text{kg}}} &\quad \scriptsize \\[5pt]
v&\approx& 5,9 \cdot 10^6 \frac{\text{m}}{\text{s}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c3f49d218cd99788e1632eb468e8a140483aed82f498c4f6b185c5189fe58bb9_light.svg)
b)
Mit der Drei-Finger-Regel für die linke Hand folgt:
Die Elektronen bewegen sich nach rechts, die Richtung der magnetischen Flussdichte zeigt in die Zeichenebene, die Lorentzkraft 
wirkt nach unten auf die Elektronen.
Der Lorentzkraft wirkt die elektrische Kraft 
entgegen. zeigt demnach nach oben. Deswegen muss die obere Platte positiv geladen sein und die elektrischen Feldlinien zeigen von oben nach unten.
Es gilt:
wirkt nach unten auf die Elektronen.
Der Lorentzkraft wirkt die elektrische Kraft entgegen. zeigt demnach nach oben. Deswegen muss die obere Platte positiv geladen sein und die elektrischen Feldlinien zeigen von oben nach unten.
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{F_{L}}&=&\overrightarrow{F_{el}} &\quad \scriptsize \\[5pt]
q \cdot v \cdot B &=& q\cdot E &\quad \scriptsize \mid\; E=\frac{U}{d} \\[5pt]
v\cdot B&=& \dfrac{U}{d} &\quad \scriptsize \mid\; :v \\[5pt]
B &=& \dfrac{U}{d\cdot v} \\[5pt]
B&=& \dfrac{1,0\cdot 10^3}{0,030\cdot 5,9\cdot 10^6} \;\text{T} \\[5pt]
B&=& 5,6\cdot 10^{-3} \;\text{T}
\end{array}\)](https://www.schullv.de/resources/formulas/83c64ba1086ea73e9dcfe6ce30dab11dcb9d4e1808b699b12020b44770e17b5c_light.svg)
c)
Mit der Energieerhaltung folgt, dass die kinetische Energie des Elektrons an Punkt A mit der Energie des elektrischen Feldes übereinstimmen muss.
![\(\begin{array}[t]{rll}
E_{kin} &\lt& E_{el} &\quad \scriptsize \\[5pt]
\frac{mv^2}{2} &\lt& q \cdot E \cdot d &\quad \scriptsize \mid \, q=e\, \text{und}\, E=\frac{U}{d}\\[5pt]
\frac{mv^2}{2} &\lt& e\cdot U &\quad \scriptsize \mid \, :e\\[5pt]
U &\gt& \dfrac{ m \cdot v^2}{2\cdot e} &\quad \scriptsize\\[5pt]
U &\gt& \dfrac{ \left(9,11 \cdot 10^{-31} kg \right) \cdot \left( 5,9 \cdot 10^6 \frac{m}{s}\right)^2}{2\cdot \left( 1,60 \cdot 10^{-19} C \right)} &\quad \scriptsize\\[5pt]
U &\gt& 100 \, V &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b6c97de108a4527a203069c90db05270170ff7c2d39a7032b13d989ddec88c63_light.svg)
d)
1. Schritt: Gleichung für die Eindringtiefe 
aufstellen
Es gilt: 
2. Schritt: Wertetabelle aufstellen
3. Schritt: Diagramm erstellen
aufstellen
Es gilt:
2. Schritt: Wertetabelle aufstellen
![\(\begin{array}[t]{rll}
E_{kin} &=& \dfrac{U\cdot q\cdot s}{d} &\quad \scriptsize \mid\;:s \\[5pt]
\dfrac{E_{kin}}{s} &=& \dfrac{U\cdot q}{d} \\[5pt]
\dfrac{s}{E_{kin}} &=& \dfrac{d}{U\cdot q} &\quad \scriptsize \mid\;\cdot E_{kin} \\[5pt]
s &=& \dfrac{E_{kin}\cdot d}{U\cdot q} \\[5pt]
s &=& \dfrac{100 \cdot 1,6\cdot 10^{-19}\cdot 0,030}{1,6\cdot 10^{-19}} \dfrac{\text{J}\cdot \text{m}}{\text{C}} \cdot \dfrac{1}{U}\\[5pt]
s&=& 3,0 \;\text{Vm}\cdot \dfrac{1}{U}
\end{array}\)](https://www.schullv.de/resources/formulas/f6d8e32e94afd74b6a76084edaf9c9ede01d6b2730caf162e64a50d46fc645f9_light.svg)
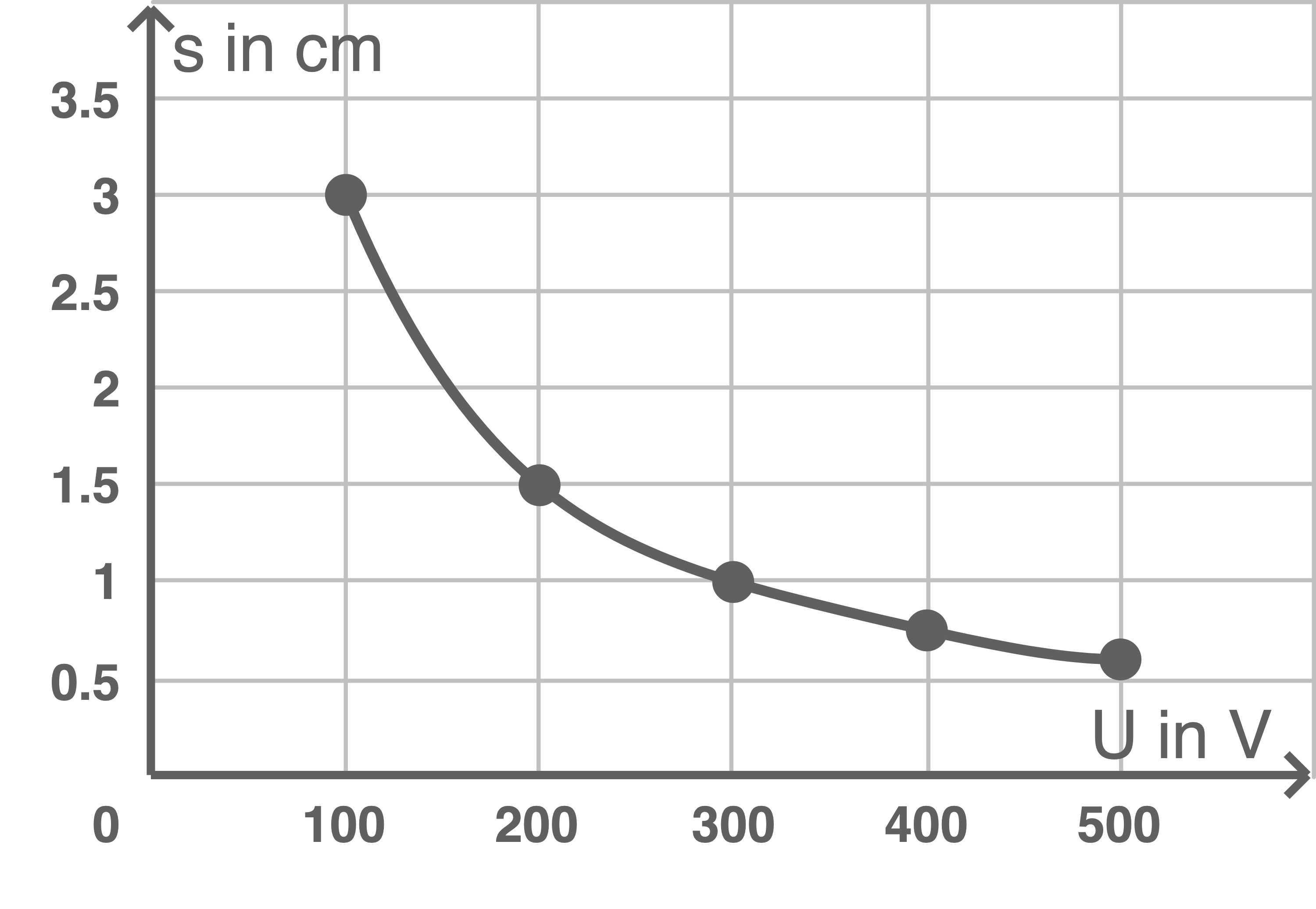
| U in V | s in cm |
|---|---|
| 100 | 3 |
| 200 | 1,5 |
| 300 | 1 |
| 400 | 0,75 |
| 500 | 0,6 |
U-s-Diagramm
e)
Sobald die Elektronen den Punkt A in Richtung des ersten Kondensators durchqueren, wirkt die elektrische Kraft nach oben (siehe Teilaufgabe b). Da die Elektronen sich nun in die entgegengesetzte Richtung bewegen, wirkt die Lorenzkraft nun in die entgegengesetzte Richtung. Somit wirkt diese auch nach oben. Folglich werden die Elektronen nach oben abgelenkt.