Aufgabe 2 – Licht
Abbildung 1 zeigt einen optischen Entfernungsmesser. Dieser kann mithilfe eines Lasers den Abstand eines anvisierten Objekts zum Gehäuse bestimmen. In den Aufgaben 1-3 werden verschiedene Experimente mit diesem Gerät beschrieben.

Abbildung 1
1.
Zunächst soll mithilfe eines Doppelspalts und eines quadratischen Schirms ein Wert für die Wellenlänge des Laserlichts ermittelt werden. Dazu wird der Laserstrahl orthogonal auf die Mitte des Schirms mit der Kantenlänge  gerichtet. Der Doppelspalt mit dem Spaltmittenabstand
gerichtet. Der Doppelspalt mit dem Spaltmittenabstand  wird im Abstand von
wird im Abstand von  zum Schirm so in den Strahlengang eingeschoben, dass Spalt- und Schirmebene parallel sind. Auf dem Schirm entsteht dadurch ein Muster aus hellen und dunklen Bereichen. Von Einflüssen der Breite der Spaltöffnungen wird abgesehen.
zum Schirm so in den Strahlengang eingeschoben, dass Spalt- und Schirmebene parallel sind. Auf dem Schirm entsteht dadurch ein Muster aus hellen und dunklen Bereichen. Von Einflüssen der Breite der Spaltöffnungen wird abgesehen.

a)
Erläutere das Schirmbild und leite dabei anhand einer geeigneten Skizze her, wie sich die Abstände der Intensitätsmaxima von der Schirmmitte berechnen lassen.
Der Abstand des Maximums 2. Ordnung zur Mitte beträgt
b)
Berechne die Wellenlänge des verwendeten Laserlichts.
c)
Überprüfe, ob die auf dem Schirm beobachtbaren Abstände von benachbarten Intensitätsmaxima gleich groß sind.
d)
Gib zwei Möglichkeiten an, wie sich die Messgenauigkeiten bei der Wellenlängenbestimmung mit dem vorliegenden Doppelspalt erhöhen lassen. Begründe deine Angaben.
(8 VP)
2.
Im Versuchsaufbau von Teilaufgabe 1 wird der Doppelspalt durch einen Einzelspalt mit variabler Breite ersetzt. Bei drei unterschiedlich eingestellten Spaltbreiten erhält man Beugungsbilder auf dem Schirm. Der Verlauf der relativen Lichtintensität in Abhängigkeit vom Abstand von der Schirmmitte ist in den Abbildungen 2a bis 2c dargestellt.
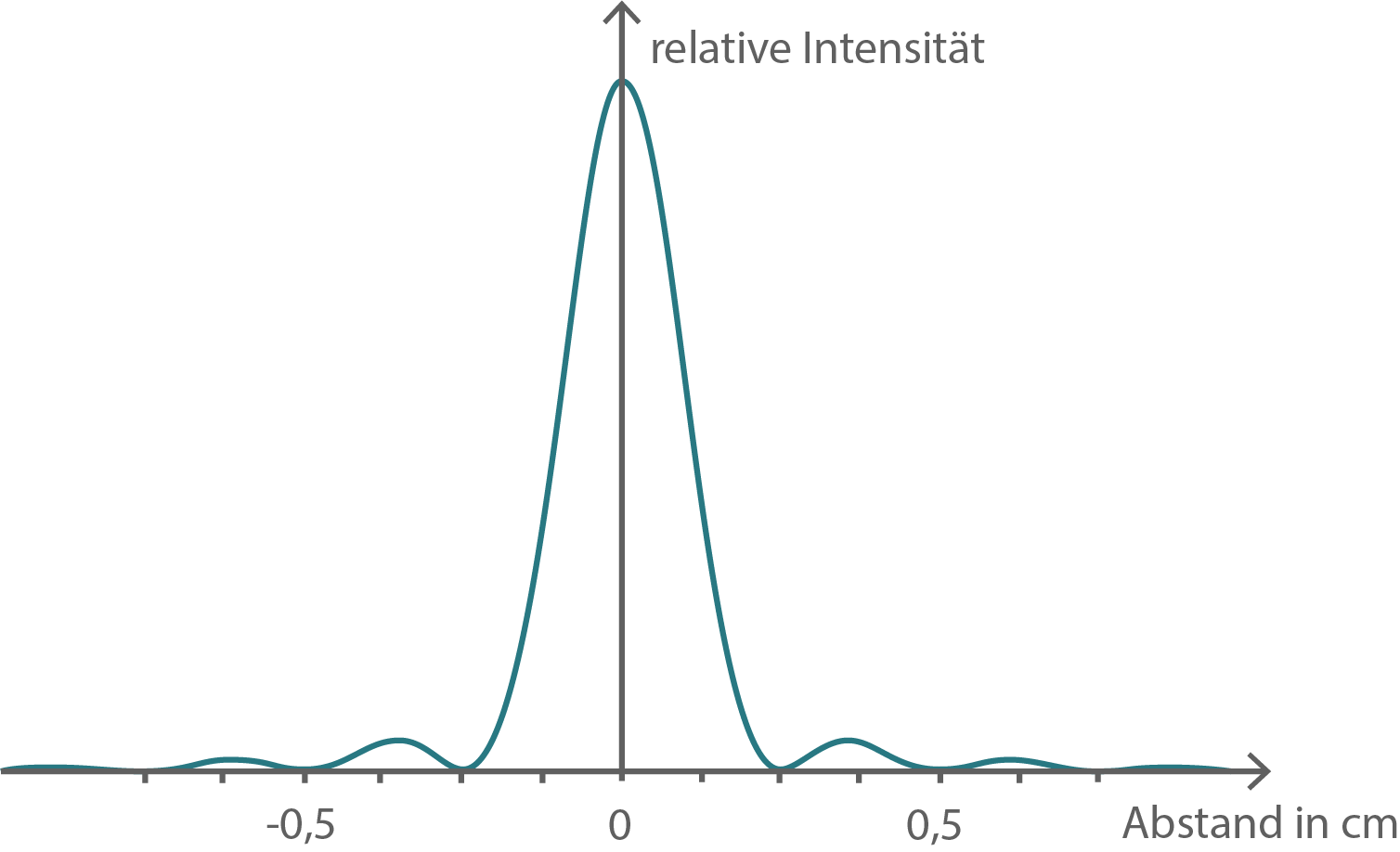
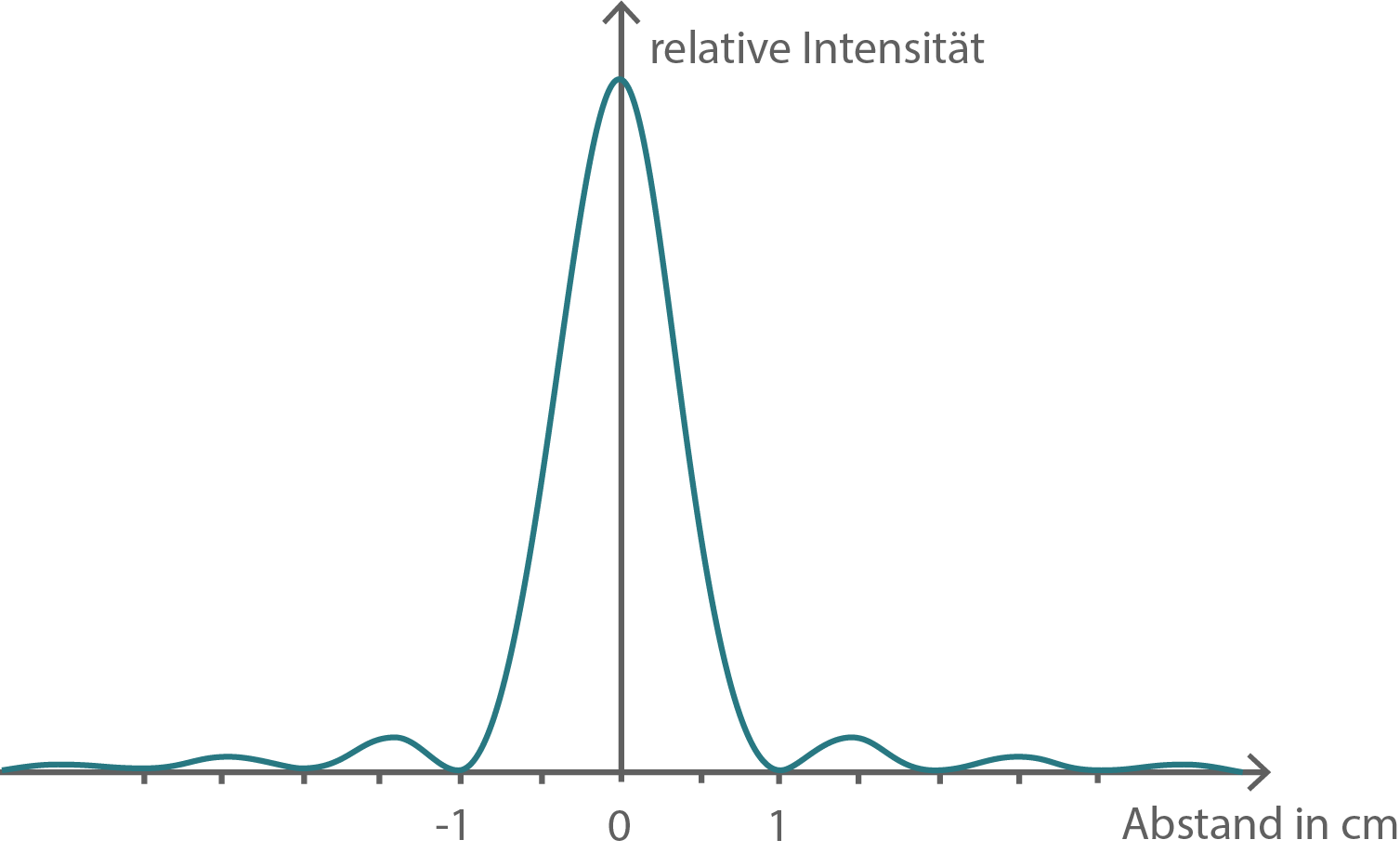
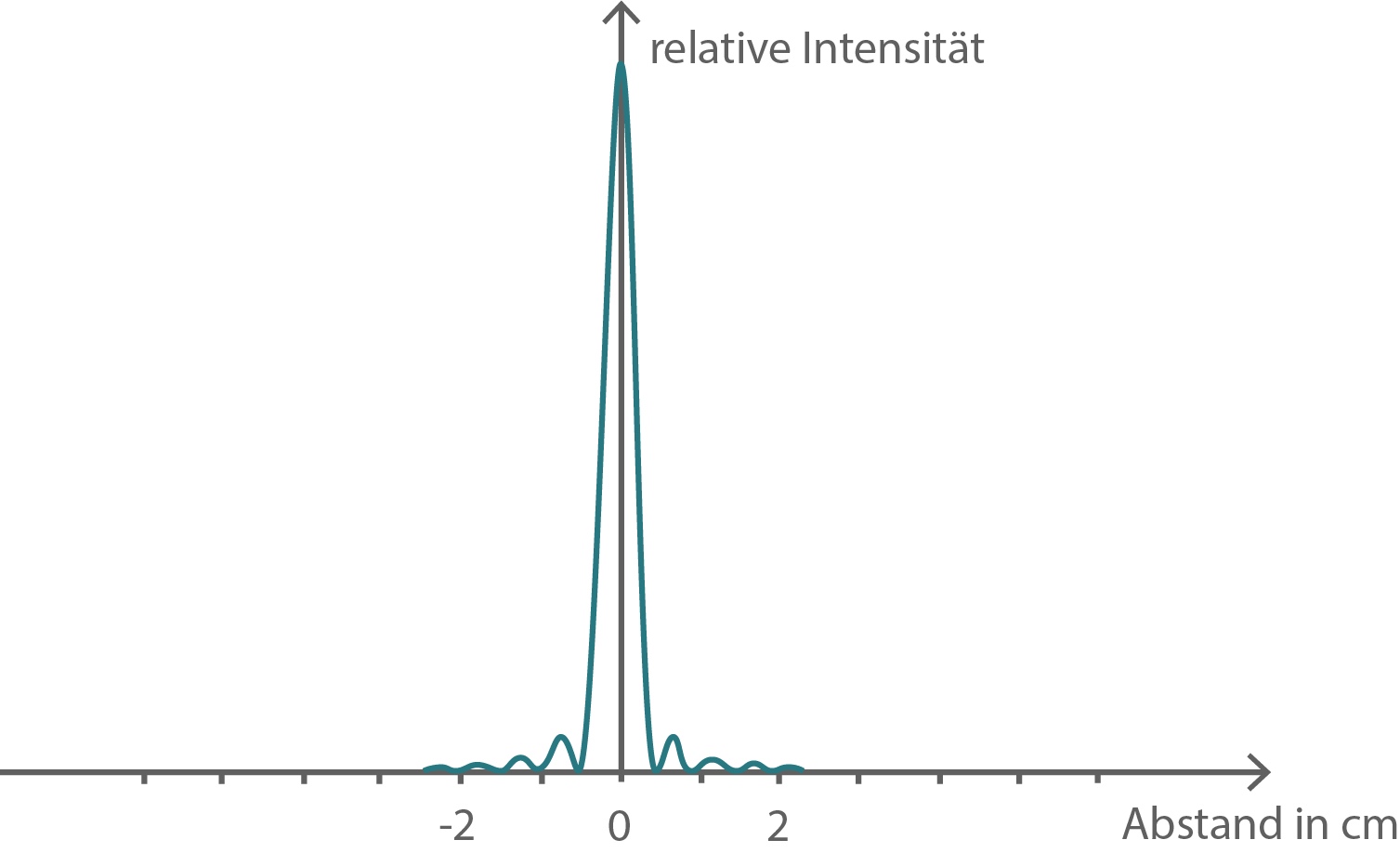

Abbildung 2a

Abbildung 2b

Abbildung 2c
a)
Ordne die drei Schaubilder nach zunehmender Spaltbreite und begründe deine angegebene Reihenfolge.
b)
Bestimme das Verhältnis von größter zu kleinster Spaltbreite.
c)
Ermittle den Bereich der Spaltbreite, bei dem bei Verwendung von Laserlicht mit der Wellenlänge  kein Intensitätsminimum auf dem Schirm vorhanden ist.
kein Intensitätsminimum auf dem Schirm vorhanden ist.
(7 VP)
3.
Es werden nun weitere Experimente mit dem Entfernungsmesser durchgeführt, bei denen tatsächlich Entfernungen bestimmt werden. Das Gerät ermittelt dazu die Laufzeit, die zwischen der Aussendung eines Laserimpulses und dem Empfang des reflektierten Impulses verstreicht. Zur Berechnung der Entfernung benutzt das Gerät die Lichtgeschwindigkeit im Vakuum. Laut Herstellerangabe darf die gemessene Laufzeit nicht weniger als  betragen.
betragen.
 gebracht. Der Raum zwischen Messgerät und Spiegel ist vollständig mit Glas ausgefüllt. Das Messgerät zeigt einen Abstand von
gebracht. Der Raum zwischen Messgerät und Spiegel ist vollständig mit Glas ausgefüllt. Das Messgerät zeigt einen Abstand von  an.
an.
 oberhalb der Wasseroberfläche. Wird er senkrecht auf die Wasseroberfläche gerichtet, so zeigt er eine Entfernung von
oberhalb der Wasseroberfläche. Wird er senkrecht auf die Wasseroberfläche gerichtet, so zeigt er eine Entfernung von  an. Die Lichtgeschwindigkeit in Wasser beträgt
an. Die Lichtgeschwindigkeit in Wasser beträgt 
a)
Bestimme den kleinstmöglichen Abstand, den man mit diesem Entfernungsmesser ermitteln kann.
In einem Versuch soll nun mithilfe des Entfernungsmessers die Lichtgeschwindigkeit im Glas bestimmt werden. Dazu wird zwischen dem Messgerät und einem Spiegel ein Glasquader der Länge
b)
Erkläre die scheinbar falsche Anzeige des Messgeräts.
c)
Bestimme die Lichtgeschwindigkeit im Glas.
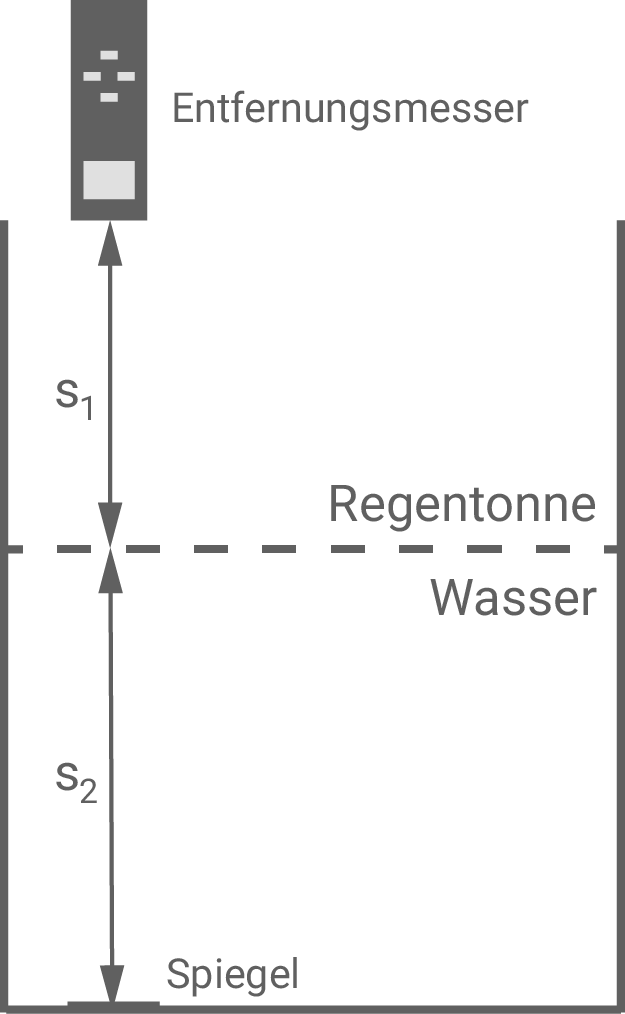
Um den Wasserstand in einer oben offenen Regentonne zu messen, wird auf den Boden der Regentonne ein Spiegel gelegt, von dem der Laserimpuls reflektiert wird. Der Entfernungsmesser befindet sich
d)
Bestimme die Höhe des Wasserstandes in der Regentonne.
(9 VP)
4.
In einem neuen Experiment werden Elektronen mit vernachlässigbarer Anfangsgeschwindigkeit in einem homogenen elektrischen Feld beschleunigt. Nach Durchlaufen einer Beschleunigungsspannung  treffen sie auf ein geeignetes Beugungsobjekt. Mithilfe des entstehenden Beugungsmusters wird die Wellenlänge
treffen sie auf ein geeignetes Beugungsobjekt. Mithilfe des entstehenden Beugungsmusters wird die Wellenlänge  in Abhängigkeit von
in Abhängigkeit von  ermittelt (siehe Tabelle 1).
ermittelt (siehe Tabelle 1).
Tabelle 1
a)
Zeige, dass für die Messwerte aus Tabelle 1 der folgende Zusammenhang gilt: 
b)
Leite den in Teilaufgabe 4a) induktiv gefundenen Zusammenhang deduktiv her.
c)
Bestimme mithilfe aller Tabellenwerte das Planck'sche Wirkungsquantum.
(6 VP)
1.
a)
Entstehung des Interferenzbildes
Die Entstehung des Interferenzbildes auf dem Schirm erfolgt aufgrund der Beugung des monochromatischen Lichts an den beiden schmalen Spalten im Doppelspalt.
Wenn Licht auf die Spalte trifft, werden die einzelnen Spalte zu neuen Quellen von Elementarwellen, die sich in alle Richtungen ausbreiten. Diese Elementarwellen überlagern sich auf dem Schirm, und an bestimmten Stellen interferieren sie konstruktiv, was zu hellen Streifen führt, während an anderen Stellen destruktive Interferenz auftritt, was zu dunklen Streifen führt.
Bedingungen für die Lage der Maxima
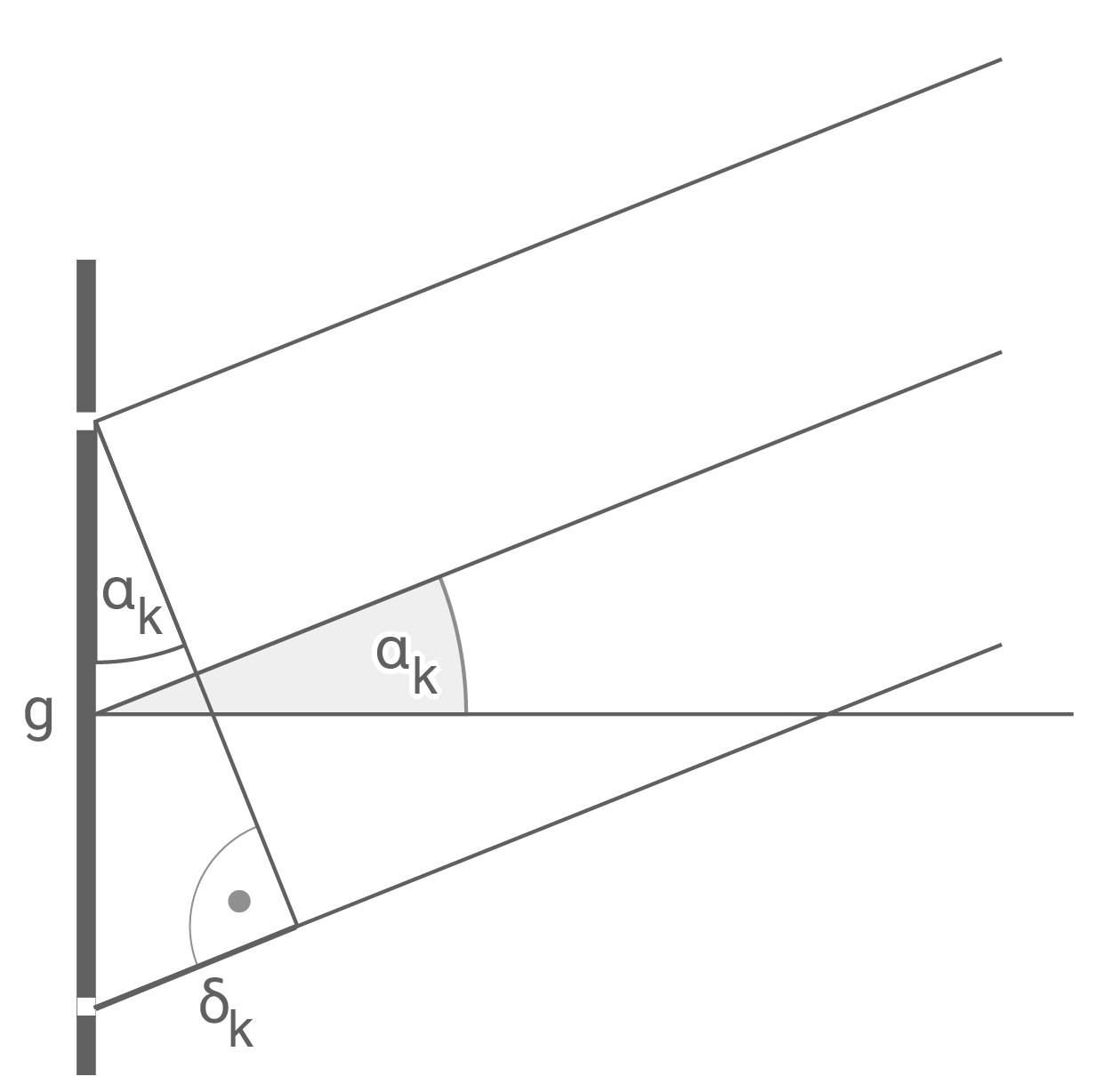 Es gilt:
Es gilt:  Für
Für  entstehen Intensitätsmaxima und für
entstehen Intensitätsmaxima und für  entstehen Intensitätsminima für
entstehen Intensitätsminima für  Für Winkel mit
Für Winkel mit  entstehen Maxima, die Minima liegen dazwischen.
entstehen Maxima, die Minima liegen dazwischen.
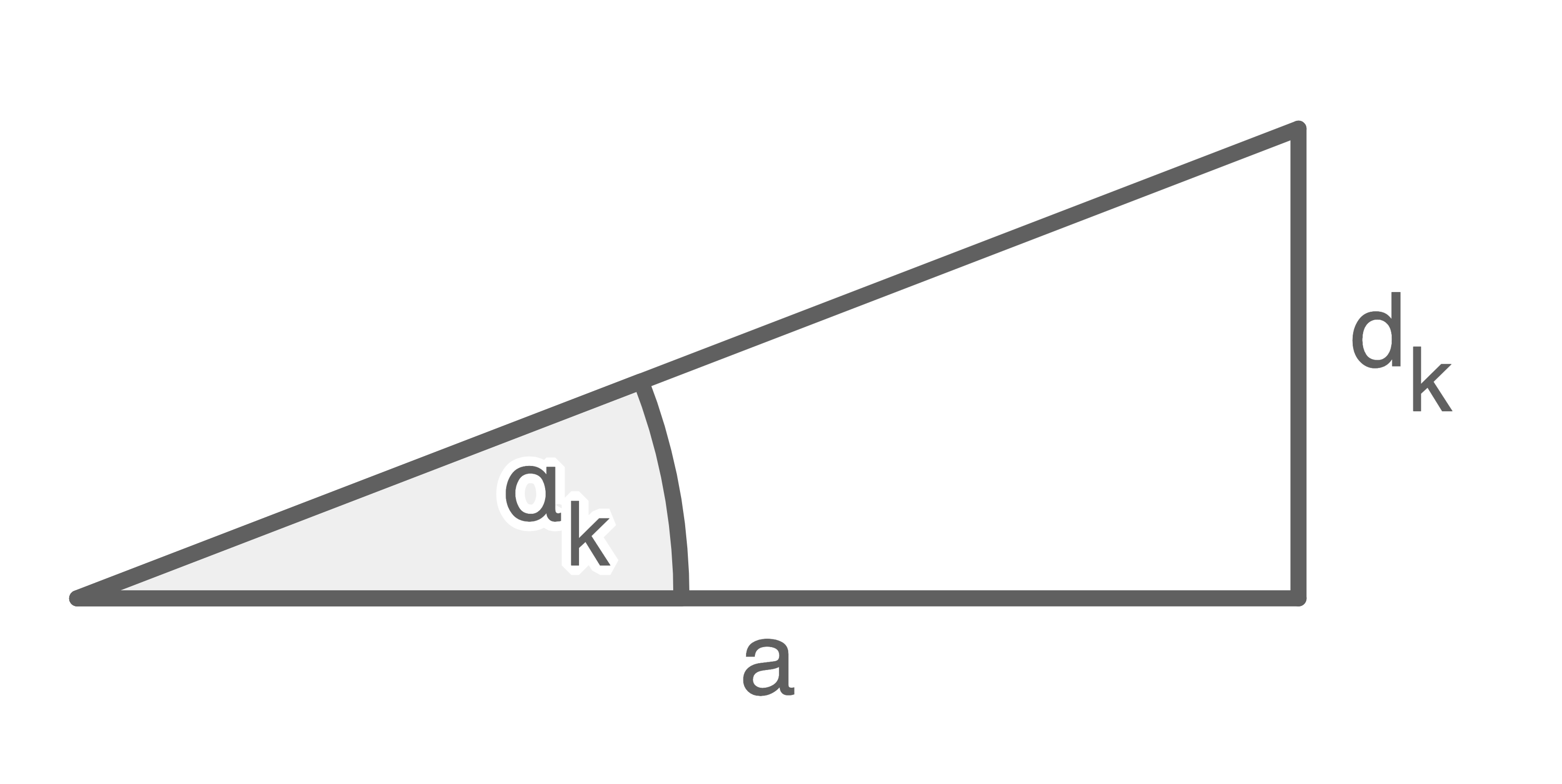

Die Abstände  der Maxima vom Maximum 0. Ordnung lassen sich mit
der Maxima vom Maximum 0. Ordnung lassen sich mit  berechnen.
berechnen.  entspricht dem Abstand des Schirms zum Doppelspalt.
entspricht dem Abstand des Schirms zum Doppelspalt.

b)
Gegeben: 


 Gesucht:
Gesucht:  Lösung:
Anwendung der Kleinwinkelnäherung
Da der Abstand des Maximums 2. Ordnung von der Mitte im Vergleich zum Schirmabstand so klein ist, kann die Kleinwinkelnäherung angewendet werden.
Für kleine Winkel
Lösung:
Anwendung der Kleinwinkelnäherung
Da der Abstand des Maximums 2. Ordnung von der Mitte im Vergleich zum Schirmabstand so klein ist, kann die Kleinwinkelnäherung angewendet werden.
Für kleine Winkel  gilt:
gilt:
![\(\begin{array}[t]{rll}
\sin (\alpha_k)&=& \tan (\alpha_k) \\[5pt]
\dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a}
\end{array}\)](https://www.schullv.de/resources/formulas/972167915c2b22e38cb536e37e596389d02aad5a28559eff5ca94ffd03f6429d_light.svg) Wellenlänge berechnen
Wellenlänge berechnen
![\(\begin{array}[t]{rll}
\dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a} &\quad \scriptsize \mid\;\cdot \dfrac{g}{k} \\[5pt]
\lambda&=& \dfrac{d_k\cdot g}{a\cdot k} \\[5pt]
\lambda&=& \dfrac{0,052 \;\text{m} \cdot 0,00012\;\text{m}}{5\;\text{m}\cdot 2} \\[5pt]
\lambda&=& 6,24 \cdot 10^{-7} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/a58395438c0fa246c9a79775a592919df3b646de128ecff0410d0e9ae14949c2_light.svg) Das verwendete Laserlicht hat eine Wellenlänge von
Das verwendete Laserlicht hat eine Wellenlänge von 
c)
Die Abstände sind gleich groß, wenn die Kleinwinkelnäherung gilt.
![\(\begin{array}[t]{rll}
\dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a} &\quad \scriptsize \mid \;\cdot a \\[5pt]
\dfrac{a\cdot k \cdot \lambda}{g} &=& d_k \\[5pt]
d_k&=&k\cdot \dfrac{a \cdot \lambda}{g}
\end{array}\)](https://www.schullv.de/resources/formulas/120f5accc71cbc759da308423b67049342945bdf472808fffcf45f09e612b387_light.svg) Die Kleinwinkelnäherung darf angewandt werden, wenn
Die Kleinwinkelnäherung darf angewandt werden, wenn  gilt.
Zu bestimmen ist folglich der größte Winkel, der auftreten kann.
gilt.
Zu bestimmen ist folglich der größte Winkel, der auftreten kann.
![\(\begin{array}[t]{rll}
\tan(\alpha_{\text{max}}) &=& \dfrac{0,15 \;\text{m}}{5,0\;\text{m}} \\[5pt]
\tan(\alpha_{\text{max}})&=& 0,03&\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha_{\text{max}} &=& 1,72^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/33b77b3f7382a228f773afac89d34e6a01418cf2f1da6ea9bca80aa1fde5dc50_light.svg) Es ist
Es ist  womit die Kleinwinkelnäherung verwendet werden darf und die Abstände gleich groß sind.
womit die Kleinwinkelnäherung verwendet werden darf und die Abstände gleich groß sind.
d)
2 Möglichkeiten, mit der die Messungenauigkeiten verringert werden:
- Vergrößerung der Schirmentfernung, hierdurch nimmt der Abstand der hellen Flecken zur Schirmmitte zu.
- Maximum höherer Ordnung wählen
2.
a)
Es gilt  ,
,  für die Beugungswinkel zu den Minima.
Je größer die Breite
für die Beugungswinkel zu den Minima.
Je größer die Breite  des Spalts, desto kleiner der Abstand der Minima zur Mitte.
In Abbildung 2a hat das Minimum erster Ordnung den Abstand
des Spalts, desto kleiner der Abstand der Minima zur Mitte.
In Abbildung 2a hat das Minimum erster Ordnung den Abstand  zur Schirmmitte.
In Abb. 2b sind es
zur Schirmmitte.
In Abb. 2b sind es  und in Abb. 2c sind es
und in Abb. 2c sind es  Die kleinste Spaltbreite ergibt sich aus dem größten Abstand.
Folglich lassen sich die folgenden Zuordnungen machen: die kleinste Spaltbreite hat Abb. 2b, die nächstgrößere Spaltbreite hat Abb. 2c und die größte Spaltbreite hat Abb. 2a.
Die kleinste Spaltbreite ergibt sich aus dem größten Abstand.
Folglich lassen sich die folgenden Zuordnungen machen: die kleinste Spaltbreite hat Abb. 2b, die nächstgrößere Spaltbreite hat Abb. 2c und die größte Spaltbreite hat Abb. 2a.
b)
1. Schritt: Prüfen ob die Kleinwinkelnäherung angewendet werden kann
 Für das Minimum aus Abb. 2 mit
Für das Minimum aus Abb. 2 mit  und
und  folgt:
folgt:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& \dfrac{d_1}{a} &\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha_1&=&\tan^{-1}\left( \dfrac{d_k}{a}\right) \\[5pt]
&\approx & 0,11^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/9d0b4b36558ae77e7b6568f0387be929a697ce6d340a89924b74ef45f0fa3f17_light.svg) Die Winkel für die Abbildungen sind noch kleiner. Somit kann die Kleinwinkelnäherung verwendet werden.
2. Schritt: Kleinwinkelnäherung anwenden
Die Winkel für die Abbildungen sind noch kleiner. Somit kann die Kleinwinkelnäherung verwendet werden.
2. Schritt: Kleinwinkelnäherung anwenden
![\(\begin{array}[t]{rll}
\sin(\alpha_1)&=& \tan(\alpha_1) \\[5pt]
\dfrac{\lambda}{b}&=& \dfrac{d_1}{a}&\quad \scriptsize \mid\;(\;)^{-1}\\[5pt]
\dfrac{b}{\lambda}&=& \dfrac{a}{d_1}&\quad \scriptsize \mid\;\cdot \lambda\\[5pt]
b&=& \dfrac{1}{d_1} \cdot a\cdot \lambda
\end{array}\)](https://www.schullv.de/resources/formulas/4f6726a4720788d1640ebfe841b72831c3a795450226d7cd1ac91c33115f2df4_light.svg) 3. Schritt: Verhältnis der Spaltbreiten bestimmen
Der größte Spalt liegt in Abb. 2a vor, der kleinste in Abb. 2b.
Der Abstand des ersten Minimums in Abb. 2a wird mit
3. Schritt: Verhältnis der Spaltbreiten bestimmen
Der größte Spalt liegt in Abb. 2a vor, der kleinste in Abb. 2b.
Der Abstand des ersten Minimums in Abb. 2a wird mit  bezeichnet, der Abstand des ersten Minimums in Abb. 2b mit
bezeichnet, der Abstand des ersten Minimums in Abb. 2b mit 



 Die Spaltbreite und der Abstand des 1. Minimums sind umgekehrt proportional und das Verhältnis beträgt somit
Die Spaltbreite und der Abstand des 1. Minimums sind umgekehrt proportional und das Verhältnis beträgt somit

Beim Einzelspalt gilt ebenfalls:
 Dabei entspricht
Dabei entspricht  dem Abstand des Minimums für
dem Abstand des Minimums für 

c)
Der größte auf dem Schirm mögliche Winkel entspricht  hierbei ist das Minimum 1. Ordnung grade noch sichtbar. Daraus folgt mit der Kleinwinkelnäherung:
hierbei ist das Minimum 1. Ordnung grade noch sichtbar. Daraus folgt mit der Kleinwinkelnäherung:
![\(\begin{array}[t]{rll}
\sin (\alpha_{\text{max}})&=& \dfrac{\lambda}{b_{\text{min}}}&\quad \scriptsize \mid\;\cdot\dfrac{b_{\text{min}}}{\sin (\alpha_{\text{max}})} \\[5pt]
b_{\text{min}}&=& \dfrac{\lambda}{\sin (\alpha_{\text{max}})} \\[5pt]
&=& \dfrac{628\cdot 10^{-9} \text{m}}{\sin (1,72^{\circ})} \\[5pt]
&=& 2,09\cdot 10^{-5} \;\text{m} \\[5pt]
&=& 20,9 \;\mu \text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/07fd4ffe47ace506a4e132a04165808fb26477349e5bcd72e56e4b49e30cbba4_light.svg) Das Minimum erster Ordnung liegt für kleinere Spaltbreiten nicht mehr auf dem Schirm.
Das Minimum erster Ordnung liegt für kleinere Spaltbreiten nicht mehr auf dem Schirm.
3.
a)
Gegeben: 
 Gesucht:
Gesucht:  Lösung:
Lösung:
![\(\begin{array}[t]{rll}
s_{\text{min}}&=& c\cdot \Delta t \\[5pt]
&=& 3 \cdot 10^8 \;\frac{\text{m}}{s} \cdot 10^{-10} \;\text{m} \\[5pt]
&=& 0,03 \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/5ddb76748527e96ee91c1ac81296c2047c70d4811314f0ca6ab3b6961810e6f4_light.svg) Das Signal durchläuft die Distanz zweimal (hin und zurück) und somit beträgt der kleinste messbare Abstand
Das Signal durchläuft die Distanz zweimal (hin und zurück) und somit beträgt der kleinste messbare Abstand 

b)
Die Lichtgeschwindigkeit im Glas ist niedriger als die Lichtgeschwindigkeit, die im Entfernungsmesser gespeichert ist. Der Entfernungsmesser misst die Laufzeit und multipliziert diese mit der in ihm gespeicherten Lichtgeschwindigkeit um die Strecke anzuzeigen. Da eine zu hohe Lichtgeschwindigkeit hinterlegt ist, zeigt er auch eine zu große Länge an.
c)
Für die Laufzeit des Signals von  gilt:
gilt:


 Somit lässt sich die Lichtgeschwindigkeit in Glas berechnen:
Somit lässt sich die Lichtgeschwindigkeit in Glas berechnen:



d)
1. Schritt: Laufzeit des Lasers berechnen


 2. Schritt: Laufzeit durch
2. Schritt: Laufzeit durch  berechnen
berechnen


 3. Schritt: Laufzeit durch
3. Schritt: Laufzeit durch  berechnen
berechnen



4.
a)
Der Zusammenhang  gilt, wenn
gilt, wenn  konstant ist.
konstant ist.
Da  konstant ist, gilt der Zusammenhang.
konstant ist, gilt der Zusammenhang.
b)
Im elektrischen Feld erhalten die Elektronen die kinetische Energie:
![\(\begin{array}[t]{rll}
\dfrac{1}{2} \cdot m \cdot v^2&=& e\cdot U&\quad \scriptsize \mid\;\cdot \dfrac{2}{m} \\[5pt]
v^2&=& \dfrac{2\cdot e\cdot U}{m}&\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
v&=& \sqrt{\dfrac{2\cdot e\cdot U}{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/698dbd7cd7049c08a7010cd6af3e50e60ead3d91bfd636e10047732be6263cc2_light.svg) Für ihren Impuls gilt:
Für ihren Impuls gilt:


 De-Broglie-Wellenlänge:
De-Broglie-Wellenlänge:

 und somit gilt dann folglich
und somit gilt dann folglich 
c)
Es gilt:
Aus der Tabelle kann aus allen Werten der Mittelwertbestimmt werden. Es folgt als Mittelwert:

 Daraus folgt der Wert für das Plank'sche Wirkungsquantum zu:
Daraus folgt der Wert für das Plank'sche Wirkungsquantum zu: