Aufgabe 3 – Felder
1.
In einem Experiment wird die magnetische Flussdichte  im Mittelpunkt von verschiedenen kreisförmigen, stromdurchflossenen Leiterschleifen gemessen. Diese besitzen jeweils eine Windung und unterscheiden sich nur in ihrem Durchmesser
im Mittelpunkt von verschiedenen kreisförmigen, stromdurchflossenen Leiterschleifen gemessen. Diese besitzen jeweils eine Windung und unterscheiden sich nur in ihrem Durchmesser  Vom Einfluss des Erdmagnetfeldes wird abgesehen.
Vom Einfluss des Erdmagnetfeldes wird abgesehen.
In der ersten Messreihe hat die Leiterschleife einen Durchmesser von
Tabelle 1 enthält die zugehörigen Messwerte.
Tabelle 1
 durchgeführt (siehe Tab. 2).
durchgeführt (siehe Tab. 2).
Tabelle 2
In der ersten Messreihe hat die Leiterschleife einen Durchmesser von
Tabelle 1 enthält die zugehörigen Messwerte.
| 5 | 0,48 |
| 10 | 0,93 |
| 15 | 1,4 |
| 20 | 1,9 |
a)
Zeige, dass die magnetische Flussdichte  proportional zur Stromstärke
proportional zur Stromstärke  ist.
ist.
Eine zweite Messreihe wird bei konstanter Stromstärke von | 1,3 | 1,9 |
| 3,2 | 0,79 |
| 5,7 | 0,43 |
| 7,4 | 0,34 |
| 10,3 | 0,25 |
b)
Stelle für diese Stromstärke die magnetische Flussdichte  in Abhängigkeit vom Durchmesser
in Abhängigkeit vom Durchmesser  in einem Diagramm dar.
in einem Diagramm dar.
c)
Formuliere eine Hypothese für den mathematischen Zusammenhang zwischen  und
und  und bestätige diese anhand der Messwerte.
und bestätige diese anhand der Messwerte.
d)
Stelle mithilfe der Messwerte aus Tabelle 2 eine Formel zur Berechnung der magnetischen Flussdichte in diesen Leiterschleifen auf.
(9 VP)
2.
In einer Versuchsanordnung befindet sich ein homogenes, scharf begrenztes Magnetfeld, dessen magnetische Flussdichte  beträgt und senkrecht in die Zeichenebene weist (siehe Abb. 1). Ein quadratischer Leiterrahmen mit der Kantenlänge
beträgt und senkrecht in die Zeichenebene weist (siehe Abb. 1). Ein quadratischer Leiterrahmen mit der Kantenlänge  und der Windungszahl
und der Windungszahl  bewegt sich mit konstanter Geschwindigkeit von
bewegt sich mit konstanter Geschwindigkeit von  in positive
in positive  -Richtung. Zum Zeitpunkt
-Richtung. Zum Zeitpunkt  befindet sich der Rahmen in der dargestellten Position bei
befindet sich der Rahmen in der dargestellten Position bei 
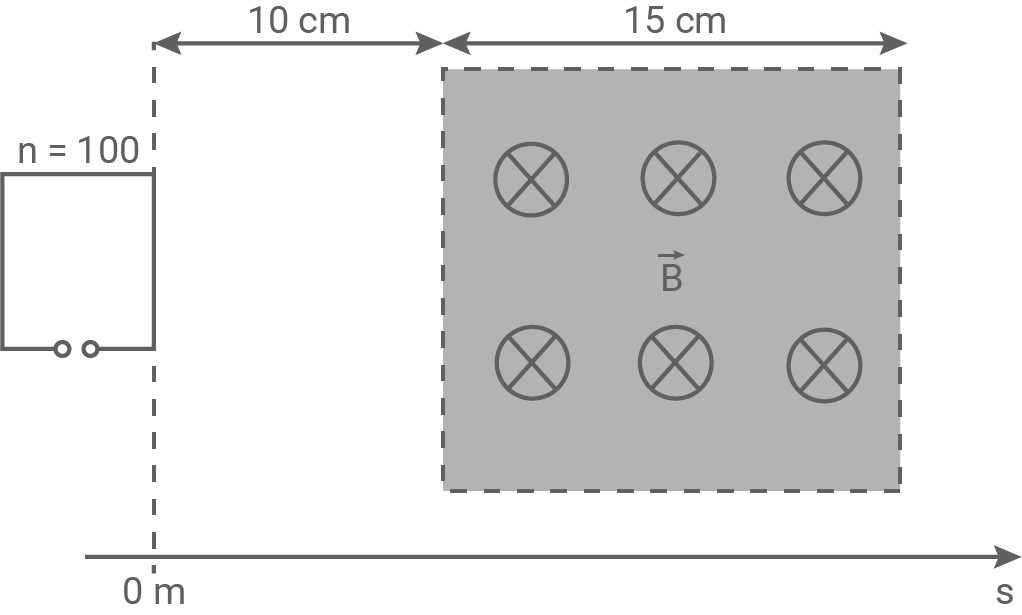
Abbildung 1
a)
Erkläre das zeitweise Auftreten einer Induktionsspannung bei der Bewegung des Rahmens.
b)
Stelle den magnetischen Fluss im Leiterrahmen für das Zeitintervall  in einem Diagramm dar.
in einem Diagramm dar.
Nun werden die Enden des Leiterrahmens mit einem ohmschen Widerstand von 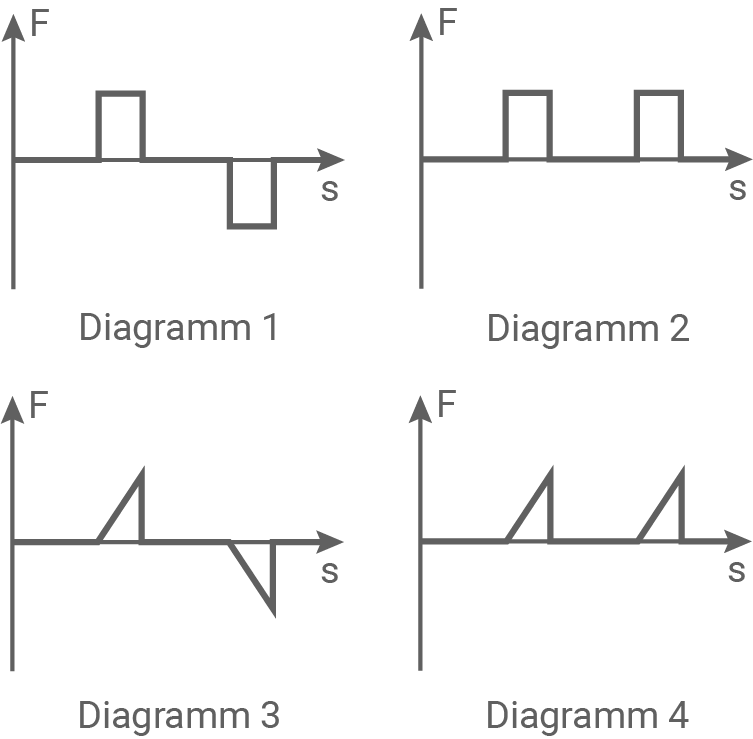
Abbildung 2
c)
Begründe, welches Diagramm den Vorgang am besten darstellt.
d)
Zeichne das von dir ausgewählte  -
- -Diagramm mit den zum Versuch passenden Zahlenwerten.
-Diagramm mit den zum Versuch passenden Zahlenwerten.
e)
Berechne die bei dem Gesamtvorgang aufzuwendende mechanische Energie.
(12 VP)
3.
Ein Drahtrahmen mit 50 Windungen wird in einem homogenen Magnetfeld gedreht (siehe Abb. 3). Im  -
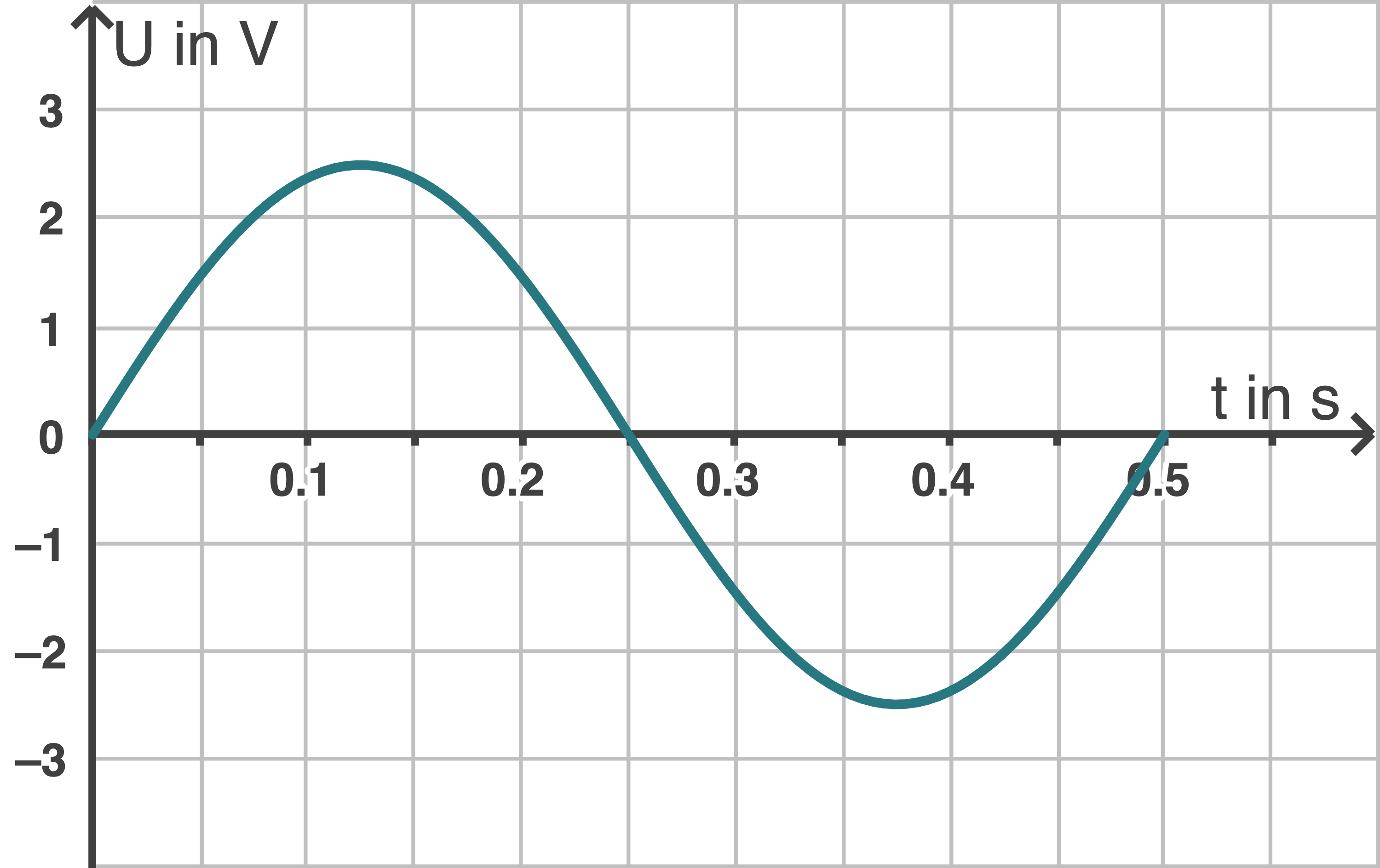
- -Diagramm der Abbildung 4 ist eine sinusförmige Wechselspannung zu sehen, die beim Drehen des Rahmens an den Anschlüssen
-Diagramm der Abbildung 4 ist eine sinusförmige Wechselspannung zu sehen, die beim Drehen des Rahmens an den Anschlüssen  und
und  gemessen wird.
gemessen wird.
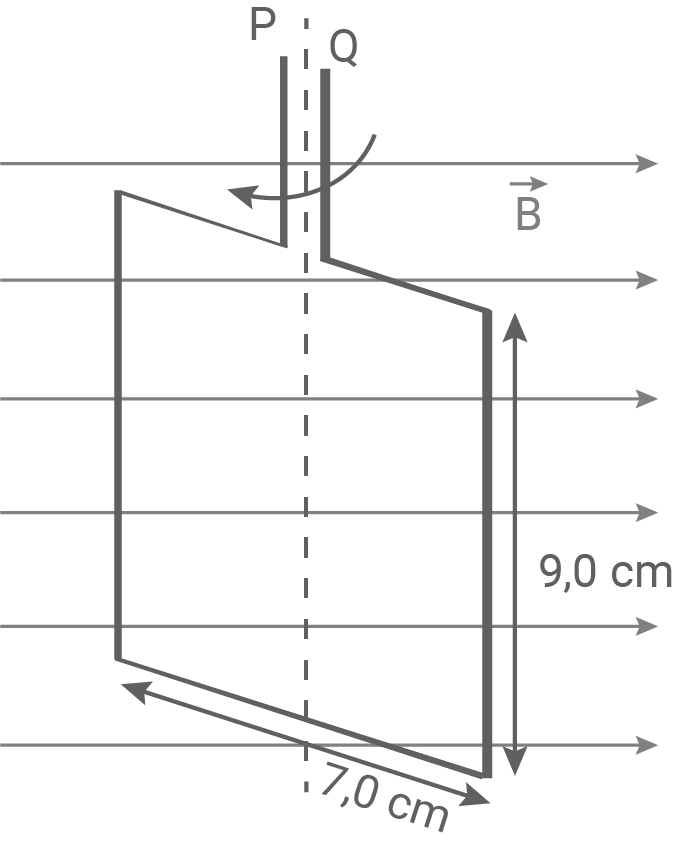
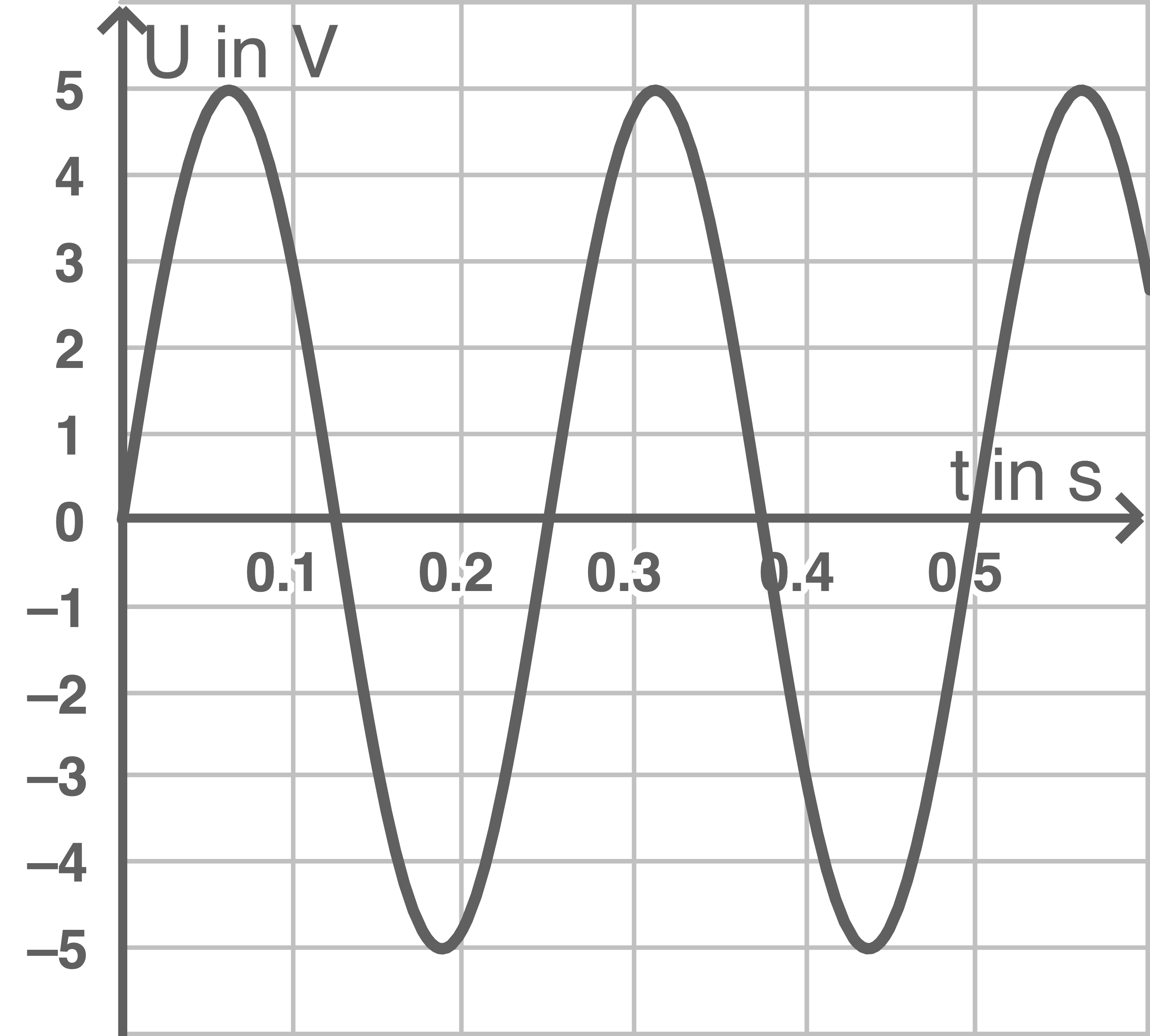

Abbildung 3

Abbildung 4
a)
Bestimme anhand des Diagramms Frequenz und Amplitude der induzierten Wechselspannung.
b)
Gib die Stellung des Rahmens relativ zu den Feldlinien zum Zeitpunkt maximaler Induktionsspannung an. Begründe deine Angabe.
c)
Bestimme die magnetische Flussdichte.
Die Drehfrequenz ist nun halb so groß wie in Teilaufgabe a).
d)
Zeichne das zugehörige  -
- -Diagramm für das Zeitintervall
-Diagramm für das Zeitintervall  .
.
(9 VP)
Lösung 1
a)
| 5 | 0,48 | 10,41 |
| 10 | 0,93 | 10,75 |
| 15 | 1,4 | 10,71 |
| 20 | 1,9 | 10,52 |
b)
-diagramm.png)
B-d-Diagramm
c)
1. Schritt: Hypothese aufstellen
Im Diagramm ist erkennbar: Für größerer Werte für  nimmt die magnetische Flussdichte
nimmt die magnetische Flussdichte  ab.
Damit ist anzunehmen, dass
ab.
Damit ist anzunehmen, dass  und
und  umgekehrt proportional zueinander sind:
umgekehrt proportional zueinander sind:  2. Schritt: Hypothese anhand der Messwerte bestätigen
Wenn die Messwertepaare jeweils das selbe
2. Schritt: Hypothese anhand der Messwerte bestätigen
Wenn die Messwertepaare jeweils das selbe  aus
aus  mit
mit  ergeben, ist die Hypothese bestätigt.
ergeben, ist die Hypothese bestätigt.
Da  für alle Messwertpaare
für alle Messwertpaare  ergibt, ist
ergibt, ist  .
.
| 1,3 | 1,9 | 2,47 |
| 3,2 | 0,79 | 2,528 |
| 5,7 | 0,43 | 2,451 |
| 7,4 | 0,34 | 2,516 |
| 10,3 | 0,25 | 2,575 |
d)
Aus Teilaufgabe 1a folgt:  Aus Teilaufgabe 1c folgt:
Aus Teilaufgabe 1c folgt:  Somit folgt insgesamt:
Somit folgt insgesamt:  bzw.
bzw. 
 Damit folgt als Formel für die magnetische Flussdichte:
Damit folgt als Formel für die magnetische Flussdichte:

Lösung 2
a)
Erklärung mittels Induktionsgesetz
Wenn der Leiterrahmen in das Magnetfeld eintaucht oder dieses verlässt, ändert sich die vom magnetischen Feld durchsetzte Fläche. Dadurch ändert sich der magnetische Fluss wegen  wodurch eine Spannung induziert wird.
Ist der Leiterrahmen ganz ins Magnetfeld eingetaucht, ändert sich die Fläche nicht. Ebenso wenn der Leiterrahmen sich nicht im Magnetfeld befindet. Hier wird folglich keine Spannung induziert.
Erklärung mittels Lorentzkraft
Wird der Leiterrahmen in das Magnetfeld eingtaucht, wirkt die Lotzentkraft auf im Leiterrahmen enthaltenenen Elektronen. Diese bewegen sich frei im Leiterrahmen und verschieben sich während des Eintauchvorgangs nach unten. Es kommt zur Ladungsunterschied, bzw. Elektronenmangel im oberen Teil des Leiterrahmens. Dadurch entsteht eine (Induktions-)Spannung.
Die Induktionsspannung bleibt konstant, bis der Leiterrahmen vollständig ins Magnetfeld eingetaucht ist. Hier ist der Ladungsunterschied wieder ausgeglichen, weswegen keine (Induktions-)Spannung mehr herrscht.
Verlässt der Leiterrahmen das Magnetfeld, so wiederholt sich der Eintauchvorgang, heißt hier entsteht wieder eine (Induktions-)Spannung.
wodurch eine Spannung induziert wird.
Ist der Leiterrahmen ganz ins Magnetfeld eingetaucht, ändert sich die Fläche nicht. Ebenso wenn der Leiterrahmen sich nicht im Magnetfeld befindet. Hier wird folglich keine Spannung induziert.
Erklärung mittels Lorentzkraft
Wird der Leiterrahmen in das Magnetfeld eingtaucht, wirkt die Lotzentkraft auf im Leiterrahmen enthaltenenen Elektronen. Diese bewegen sich frei im Leiterrahmen und verschieben sich während des Eintauchvorgangs nach unten. Es kommt zur Ladungsunterschied, bzw. Elektronenmangel im oberen Teil des Leiterrahmens. Dadurch entsteht eine (Induktions-)Spannung.
Die Induktionsspannung bleibt konstant, bis der Leiterrahmen vollständig ins Magnetfeld eingetaucht ist. Hier ist der Ladungsunterschied wieder ausgeglichen, weswegen keine (Induktions-)Spannung mehr herrscht.
Verlässt der Leiterrahmen das Magnetfeld, so wiederholt sich der Eintauchvorgang, heißt hier entsteht wieder eine (Induktions-)Spannung.
b)
1. Schritt: Änderung des magnetischen Flusses in Abschnitte einteilen
Der Magnetische Fluss  ist von der Fläche abhängig.
ist von der Fläche abhängig.
Wenn die Leiterschleife in das Magnetfeld bei eintritt, steigt der magnetische Fluss an.
Je mehr Fläche der Leiterschleife sich im Magnetfeld befindet, desto höher ist der magnetische Fluss.
Bei
eintritt, steigt der magnetische Fluss an.
Je mehr Fläche der Leiterschleife sich im Magnetfeld befindet, desto höher ist der magnetische Fluss.
Bei  befindet sich die Leiterschleife vollständig im Magnetfeld. Hier ist der Fluss maximal.
Sobald die Leiterschleife bei
befindet sich die Leiterschleife vollständig im Magnetfeld. Hier ist der Fluss maximal.
Sobald die Leiterschleife bei  austritt, sinkt der magnetische Fluss.
Der magnetische Fluss ist wieder null, wenn die Leiterschleife bei
austritt, sinkt der magnetische Fluss.
Der magnetische Fluss ist wieder null, wenn die Leiterschleife bei  vollständig aus dem Magnetfeld ausgetreten ist.
2. Schritt: Zeitpunkte der Abschnitte berechnen
vollständig aus dem Magnetfeld ausgetreten ist.
2. Schritt: Zeitpunkte der Abschnitte berechnen
![\(\begin{array}[t]{rll}
t &=& \dfrac{s}{v} &\quad \scriptsize \\[5pt]
&=& \dfrac{s}{5\, \frac{\text{cm}}{\text{s}}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/92da412abab9e8c7c7d6b99dfd1d841cd9f7aa4058a7a132e9ea1839dcface71_light.svg)
3. Schritt: Maximalen magnetischen Fluss berechnen
![\(\begin{array}[t]{rll}
\Phi_{max} &=& A \cdot B &\quad \scriptsize \\[5pt]
&=& \left( 0,05\,\text{m} \cdot 0,05\, \text{m} \right) \cdot 2,0 \,\text{T} &\quad \scriptsize \\[5pt]
&=& 0,005 \,\text{Tm}^2 &\quad \scriptsize \\[5pt]
&=& 5 \cdot 10^{-3} \text{Tm}^2 &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5b186ad6ee13ecd1ba4cbc6f7a266cb8a583190e7a0a999da9fa595a31f0554c_light.svg) 4. Schritt: Diagramm erstellen
4. Schritt: Diagramm erstellen
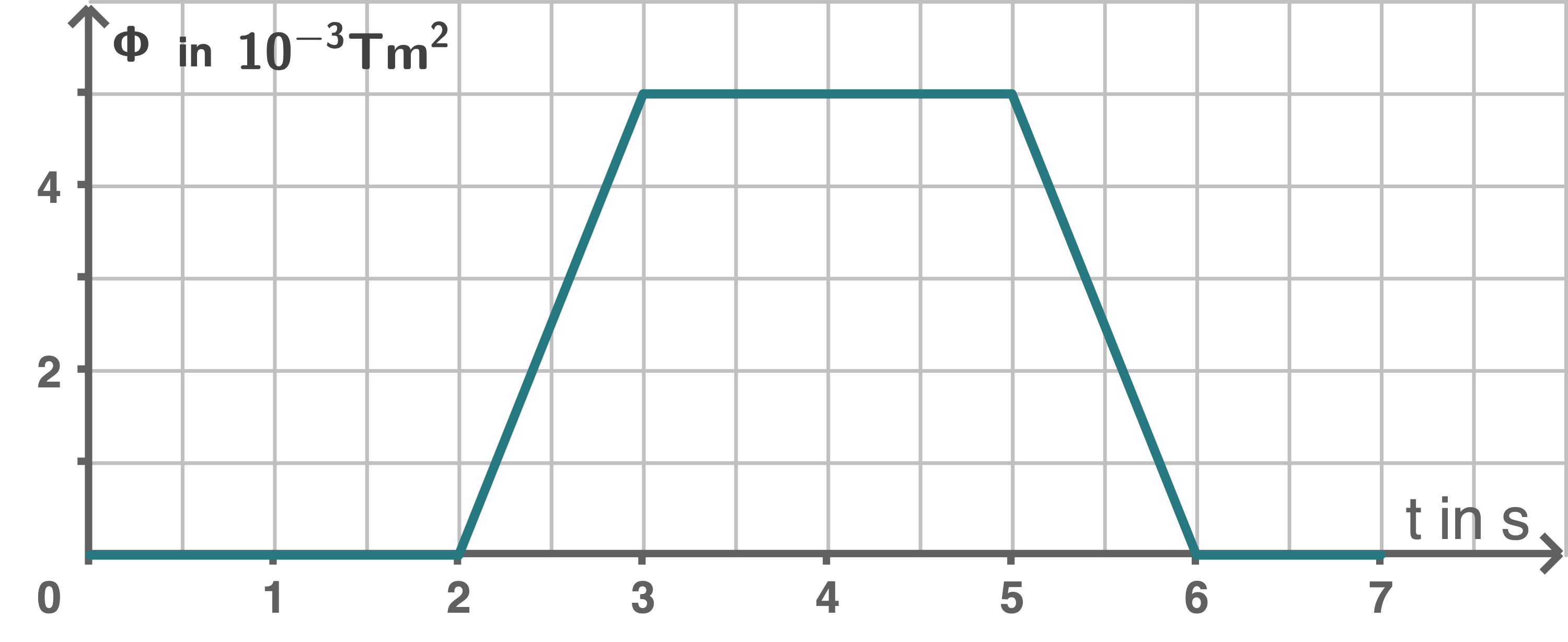
Wenn die Leiterschleife in das Magnetfeld bei
| 10 | 2 |
| 15 | 3 |
| 25 | 5 |
| 30 | 6 |

c)
Es gilt  Somit fließt nur ein Strom, wenn eine Spannung induziert wird, heißt, wenn sich der magnetische Fluss ändert.
Die Lenz'sche Regel besagt, dass der Induktionsstrom immer seiner Ursache entgegenwirkt. Es wird also der Änderung des magnetischen Flusses entgegengewirkt.
Es finden zwei Flussänderungen statt: Beim Eintauchen und beim Verlassen des Magnetfeldes.
Der Änderung wird hierbei entgegengewirkt, indem die Bewegung gebremst wird. Dadurch steigt die zum Bewegen des Rahmens benötigte Kraft.
Es entsteht immer eine konstante Kraft, welche entgegengesetzt der Bewegungsrichtung wirkt, da die Änderung der Flussänderung jeweils einen konstanten Strom erzeugt. Damit hat die entstehende Kraft immer das gleiche Vorzeichen.
Folglich ist das Diagramm
Somit fließt nur ein Strom, wenn eine Spannung induziert wird, heißt, wenn sich der magnetische Fluss ändert.
Die Lenz'sche Regel besagt, dass der Induktionsstrom immer seiner Ursache entgegenwirkt. Es wird also der Änderung des magnetischen Flusses entgegengewirkt.
Es finden zwei Flussänderungen statt: Beim Eintauchen und beim Verlassen des Magnetfeldes.
Der Änderung wird hierbei entgegengewirkt, indem die Bewegung gebremst wird. Dadurch steigt die zum Bewegen des Rahmens benötigte Kraft.
Es entsteht immer eine konstante Kraft, welche entgegengesetzt der Bewegungsrichtung wirkt, da die Änderung der Flussänderung jeweils einen konstanten Strom erzeugt. Damit hat die entstehende Kraft immer das gleiche Vorzeichen.
Folglich ist das Diagramm  das Richtige.
das Richtige.
d)
1. Schritt: Maximale Krafteinwirkung berechnen
Auf den Leiterrahmen wirkt die Lorentzkraft:




 Es gilt:
Es gilt:  Auf einzelne Ladungen wirkt die Lorentzkraft
Auf einzelne Ladungen wirkt die Lorentzkraft  Für die Spannung
Für die Spannung  die in
die in  Schleifen erzeugt wirkt, folgt:
Schleifen erzeugt wirkt, folgt:
![\(\begin{array}[t]{rll}
U&=& n\cdot E\cdot d \\[5pt]
&=& n\cdot \dfrac{F_q}{q}\cdot d \\[5pt]
&=& n\cdot \dfrac{q\cdot v\cdot B}{q}\cdot d \\[5pt]
&=& n\cdot v\cdot B\cdot d
\end{array}\)](https://www.schullv.de/resources/formulas/a3b44dfba7262b58778c73dc425280e18ebd3ad8917dc3de8352ffbf681e927a_light.svg) Somit ergibt sich die Bremskraft zu:
Somit ergibt sich die Bremskraft zu:
![\(\begin{array}[t]{rll}
F_B&=& n\cdot B\cdot I\cdot d\\[5pt]
&=& n\cdot B\cdot \dfrac{U}{R}\cdot d \\[5pt]
&=& n\cdot B\cdot \dfrac{n\cdot v\cdot B\cdot d}{R}\cdot d \\[5pt]
&=& \dfrac{n^2\cdot B^2\cdot d^2\cdot v}{R} \\[5pt]
&=& \dfrac{100^2\cdot 2,0^2\cdot 0,05^2\cdot 0,05}{10}\;\text{N} \\[5pt]
&=& 0,50\;\text{N}
\end{array}\)](https://www.schullv.de/resources/formulas/95bb538c00d942919dd3202c30a870c9c7dff4c603673095781cdb485be133ae_light.svg) 2. Schritt: Zurückgelegte Streckenstücke bestimmen, zu welchen sich die Kraft ändert
Die Kraft ändert sich, sobald sich die rechte und linke Leiterrahmenkant in bzw. aus dem Magnetfeld bewegen. Dies ist der Fall bei
2. Schritt: Zurückgelegte Streckenstücke bestimmen, zu welchen sich die Kraft ändert
Die Kraft ändert sich, sobald sich die rechte und linke Leiterrahmenkant in bzw. aus dem Magnetfeld bewegen. Dies ist der Fall bei  cm,
cm, 
 und
und  3. Schritt: Diagramm zeichnen
3. Schritt: Diagramm zeichnen
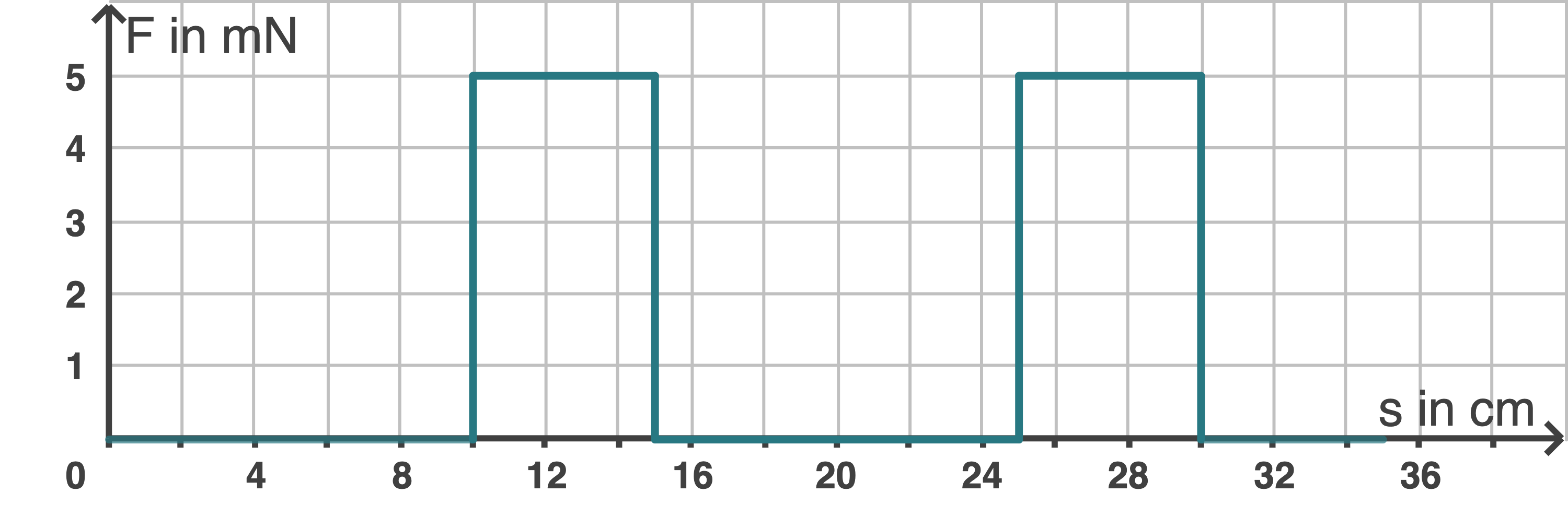

e)
Die aufzuwendende mechanische Energie entspricht der zu verichtenden Arbeit, also  . Die Arbeit muss dabei in verschiedene Abschnitte eingeteilt werden.
. Die Arbeit muss dabei in verschiedene Abschnitte eingeteilt werden.


 Dabei entspricht der Eintritt der Phase, in welcher sich die rechte, nicht aber die linke Kante im Magnetfeld befindet. Beim Austritt entsprechend umgekehrt.
In beiden Fällen ist
Dabei entspricht der Eintritt der Phase, in welcher sich die rechte, nicht aber die linke Kante im Magnetfeld befindet. Beim Austritt entsprechend umgekehrt.
In beiden Fällen ist  da dies die Strecke ist, entlang derer die Kraft wirkt.
Damit folgt mit
da dies die Strecke ist, entlang derer die Kraft wirkt.
Damit folgt mit  und
und  Es muss genauso viel Energie aufgewendet werden den Leiterrahmen aus dem Magnetfeld zu bringen, wie aufgewendet werden muss um den Leiterrahmen in das Magnetfeld zu bringen.
Es muss genauso viel Energie aufgewendet werden den Leiterrahmen aus dem Magnetfeld zu bringen, wie aufgewendet werden muss um den Leiterrahmen in das Magnetfeld zu bringen.
Die insgesamt aufzuwendende mechanische Energie ist somit .
.
Die insgesamt aufzuwendende mechanische Energie ist somit
Lösung 3
a)
Die Frequenz der induzierten Wechselspannung beträgt:
![\(\begin{array}[t]{rll}
f &=& \dfrac{1}{T} &\quad \scriptsize \\[5pt]
&=& \dfrac{1}{0,25 \, \text{s}} &\quad \scriptsize \\[5pt]
&=& 4 \, \text{Hz} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bde0b2fbffe592e93070e5572d426702ad18ea47db3c3de18225c227fb2e4426_light.svg) Die Amplitude kann aus Abbildung 4 abgelesen werden zu
Die Amplitude kann aus Abbildung 4 abgelesen werden zu 
b)
Die Induktionsspannung ist maximal, wenn die stärkste Flächenänderung herrscht.
Die größte Flächenänderung tritt auf, sobald sich die Rahmenfläche parallel zu den Feldlinien befindet.
c)
Gegeben: 

 Gesucht:
Gesucht:  Lösung:
Lösung:

 Der Leiterrahmen dreht sich im Kreis, also um die Strecke
Der Leiterrahmen dreht sich im Kreis, also um die Strecke  Aus Abbildung 3 wird
Aus Abbildung 3 wird 
 abgelesen.
Die Umlaufdauer für eine Umdrehung wird aus Abbildng 4 abgelesen:
abgelesen.
Die Umlaufdauer für eine Umdrehung wird aus Abbildng 4 abgelesen:  Somit folgt:
Somit folgt:
![\(\begin{array}[t]{rll}
v&=& \dfrac{2\cdot \pi \cdot r}{T} \\[5pt]
&=& \dfrac{2\cdot \pi \cdot 0,035\;\text{m}}{0,25 \;\text{s}} \\[5pt]
&=& 0,88 \;\frac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/ac18e5e13fc531dbfe95d2c8c4553b3d1cd5221591df56062f0450a709b78f22_light.svg) Und daraus folgt die magnetische Flussdichte zu:
Und daraus folgt die magnetische Flussdichte zu:
d)
1. Schritt: Die neue Periodendauer bestimmen
![\(\begin{array}[t]{rll}
f_{neu} &=& f \cdot \frac{1}{2} &\quad \scriptsize \\[5pt]
f_{neu} &=& 4 \, \text{Hz} \cdot \frac{1}{2} &\quad \scriptsize \\[5pt]
f_{neu} &=& 2\, \text{Hz} &\quad \scriptsize \\[5pt]
\frac{1}{T_{neu}} &=& 2\, \text{Hz} &\quad \scriptsize \mid \, \cdot T_{neu}\\[5pt]
1 &=& 2\, \text{Hz} \cdot T_{neu} &\quad \scriptsize \mid \, : 2\, \text{Hz}\\[5pt]
T_{neu} &=& 0,5 \, \text{s} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/072fbea176fd6a6633ea9cd0d50ee4e58ed4d4abb070b8164dfef5b13fa81f66_light.svg) Die Periodendauer ist mit der langsameren Drehfrequenz doppelt so groß wie zuvor.
2. Schritt: Berechnung der induzierten Spannung
Anhand der Formel
Die Periodendauer ist mit der langsameren Drehfrequenz doppelt so groß wie zuvor.
2. Schritt: Berechnung der induzierten Spannung
Anhand der Formel  in Teilaufgabe c) ist ersichtlich, dass
in Teilaufgabe c) ist ersichtlich, dass  gilt. Somit halbiert sich die induzierte Spannung auf
gilt. Somit halbiert sich die induzierte Spannung auf  3. Schritt: Diagramm zeichnen
3. Schritt: Diagramm zeichnen