Aufgabe 1 – Mechanische Schwingungen
1.
Ein Körper der Masse  wird an einer Feder befestigt, die auf Zug und Druck belastbar ist. Der Körper wird ausgelenkt und losgelassen (siehe Abb. 1). Er schwingt anschließend harmonisch. Das Diagramm in Abbildung 2 zeigt die Bewegungsenergie
wird an einer Feder befestigt, die auf Zug und Druck belastbar ist. Der Körper wird ausgelenkt und losgelassen (siehe Abb. 1). Er schwingt anschließend harmonisch. Das Diagramm in Abbildung 2 zeigt die Bewegungsenergie  des Körpers in Abhängigkeit von seiner Auslenkung
des Körpers in Abhängigkeit von seiner Auslenkung  aus der Gleichgewichtslage. Energieverluste durch Reibung und die Masse der Feder werden vernachlässigt.
aus der Gleichgewichtslage. Energieverluste durch Reibung und die Masse der Feder werden vernachlässigt.
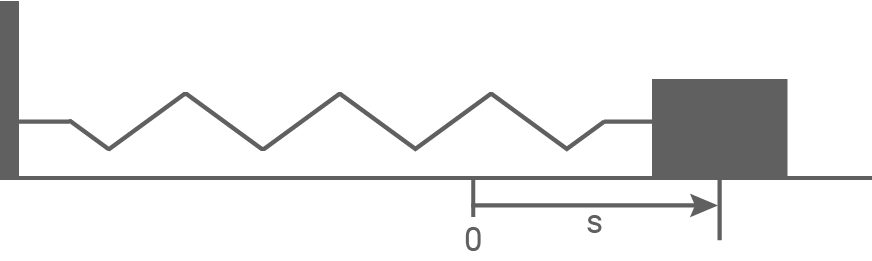
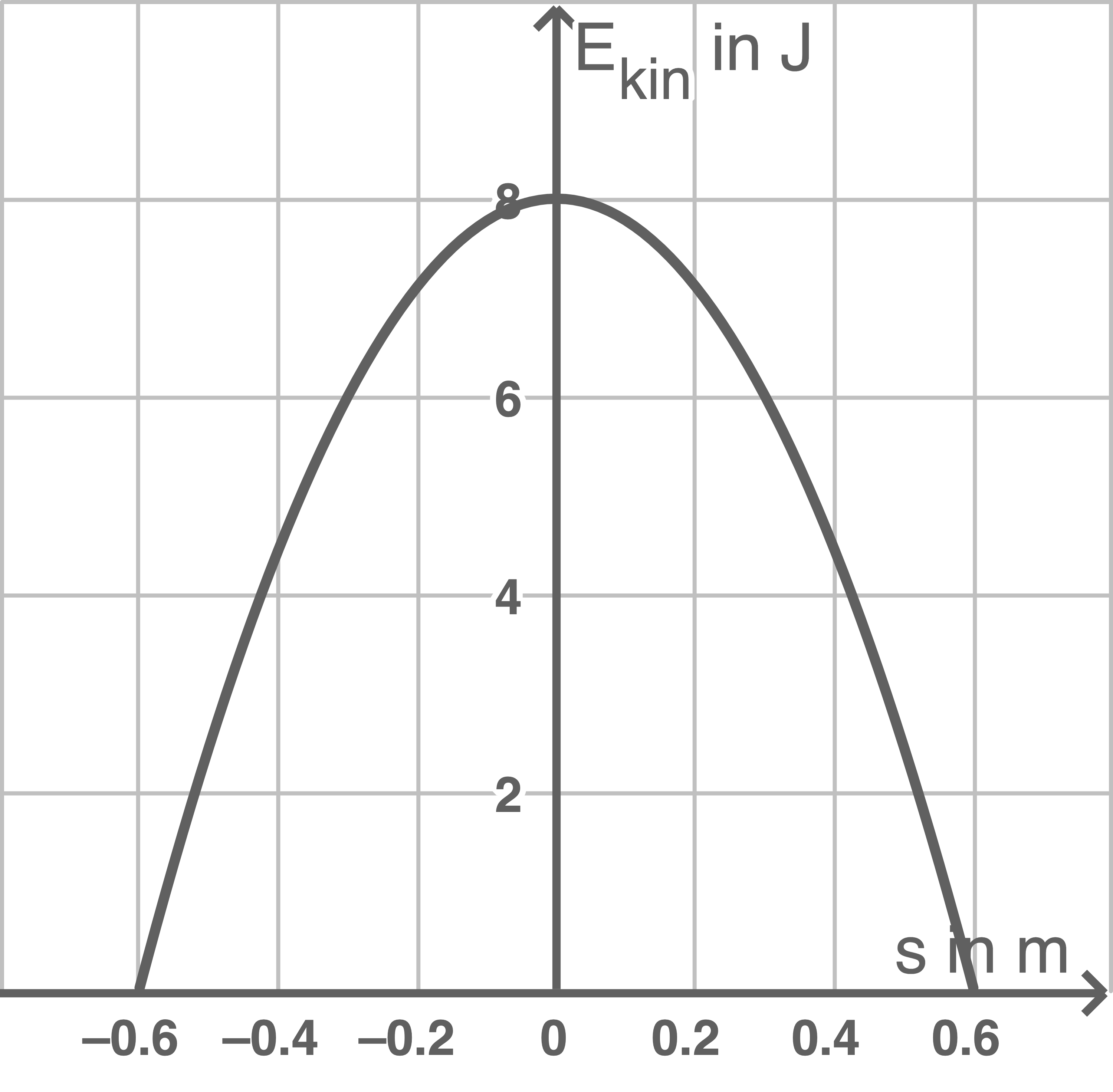

Abbildung 1

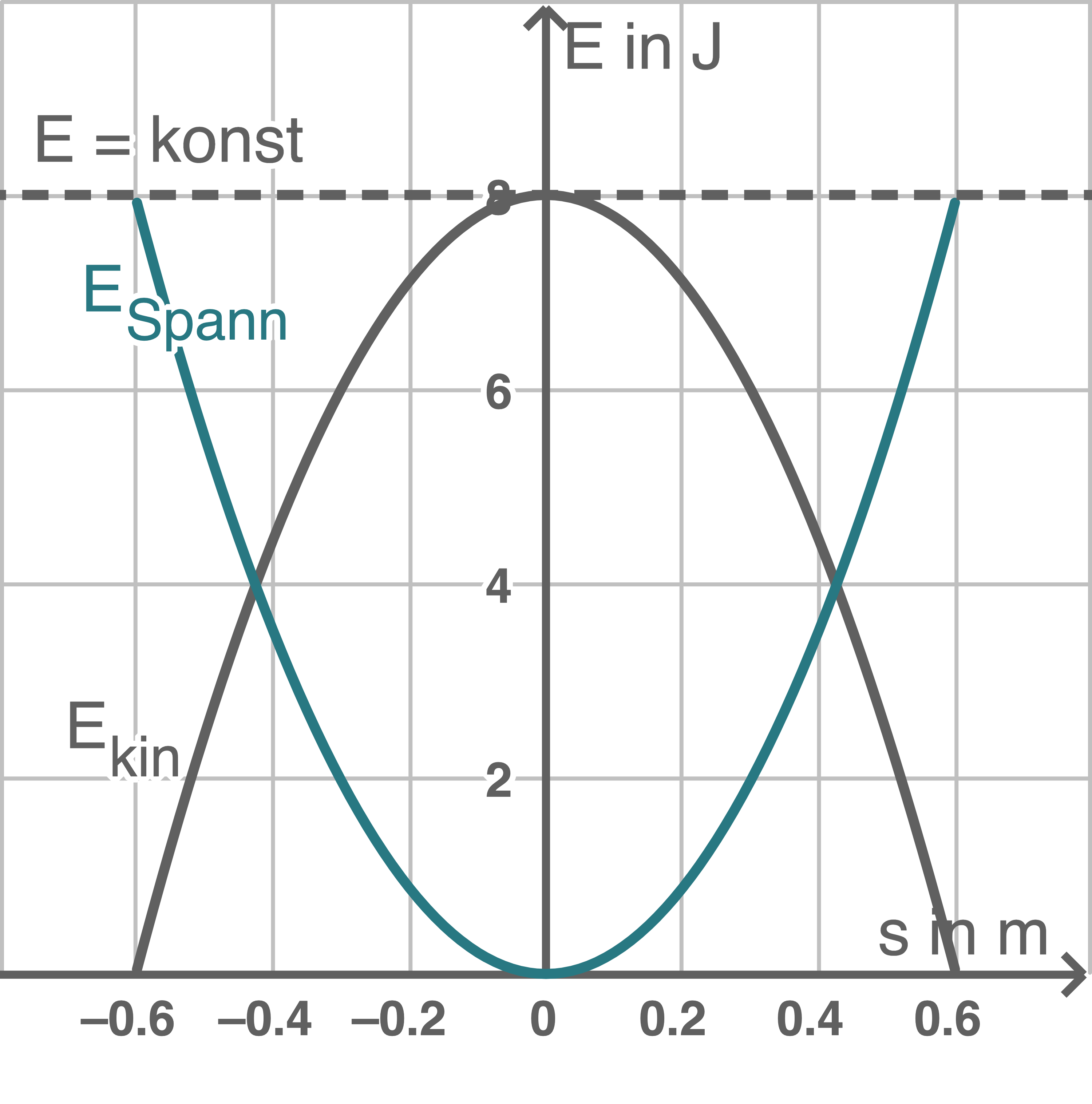
Abbildung 2
a)
Gib die Amplitude der Schwingung an.
b)
Bestimme den Betrag der maximalen Geschwindigkeit  des Körpers.
des Körpers.
c)
Bestimme die Auslenkungen, bei denen der Betrag der Geschwindigkeit  ist.
ist.
d)
Berechne die Richtgröße  der Feder.
der Feder.
e)
Skizziere den Verlauf der Spannenergie in Abhängigkeit der Auslenkung  unter Verwendung von Abbildung 2 und begründe dein Vorgehen.
unter Verwendung von Abbildung 2 und begründe dein Vorgehen.
(10 VP)
2.
In einem Schülerversuch werden Pendelschwingungen untersucht. Als Pendel dienen Stangen unterschiedlicher Länge  die am oberen Ende drehbar, reibungsarm aufgehängt sind. Sie werden um denselben kleinen Winkel ausgelenkt und losgelassen. Es wird jeweils die Dauer
die am oberen Ende drehbar, reibungsarm aufgehängt sind. Sie werden um denselben kleinen Winkel ausgelenkt und losgelassen. Es wird jeweils die Dauer  von 10 Perioden bei den verschiedenen Stangenpendeln gemessen. Tabelle 1 zeigt die Messergebnisse.
von 10 Perioden bei den verschiedenen Stangenpendeln gemessen. Tabelle 1 zeigt die Messergebnisse.
Tabelle 1
Es wird vermutet, dass die Periodendauer  der untersuchten Stangenpendel proportional zu
der untersuchten Stangenpendel proportional zu  ist.
ist.
 berechnen kann.
berechnen kann.  ist die Erdbeschleunigung und
ist die Erdbeschleunigung und  eine Konstante.
eine Konstante.
| Länge |
Dauer |
|---|---|
a)
Zeichne ein geeignetes Diagramm und bestätige damit die Vermutung.
b)
Bestimme mithilfe aller Messwerte eine Gleichung für die Periodendauer  als Funktion der Stangenlänge
als Funktion der Stangenlänge  .
.
Eine Recherche ergibt, dass man die Periodendauer solcher Stangenpendel mit der Gleichung
c)
Bestimme für die untersuchten Stangenpendel die Konstante 
(8 VP)
3.
Am linken Ende eines horizontalen, linearen Wellenträgers der Länge  befindet sich ein Erreger
befindet sich ein Erreger  , am rechten Ende ein Erreger
, am rechten Ende ein Erreger  Beide Erreger schwingen harmonisch mit der Frequenz
Beide Erreger schwingen harmonisch mit der Frequenz  und der Amplitude
und der Amplitude 
Zum Zeitpunkt beginnt
beginnt  aus der Gleichgewichtslage nach unten zu schwingen, während
aus der Gleichgewichtslage nach unten zu schwingen, während  aus der Gleichgewichtslage mit seiner Schwingung nach oben beginnt. Nach
aus der Gleichgewichtslage mit seiner Schwingung nach oben beginnt. Nach  treffen die von
treffen die von  und
und  ausgehenden Wellen aufeinander.
ausgehenden Wellen aufeinander.
 dar.
dar.
 gleichphasig nach oben.
gleichphasig nach oben.
Zum Zeitpunkt
a)
Bestimme die Wellenlänge der von den Erregern ausgehenden Wellen.
b)
Erkläre, weshalb sich die Mitte des Wellenträgers während des gesamten Versuchs nicht bewegt.
c)
Zeichne das Momentanbild des Wellenträgers zum Zeitpunkt  Gib alle Punkte des Wellenträgers an, die zu diesem Zeitpunkt in Ruhe sind.
Gib alle Punkte des Wellenträgers an, die zu diesem Zeitpunkt in Ruhe sind.
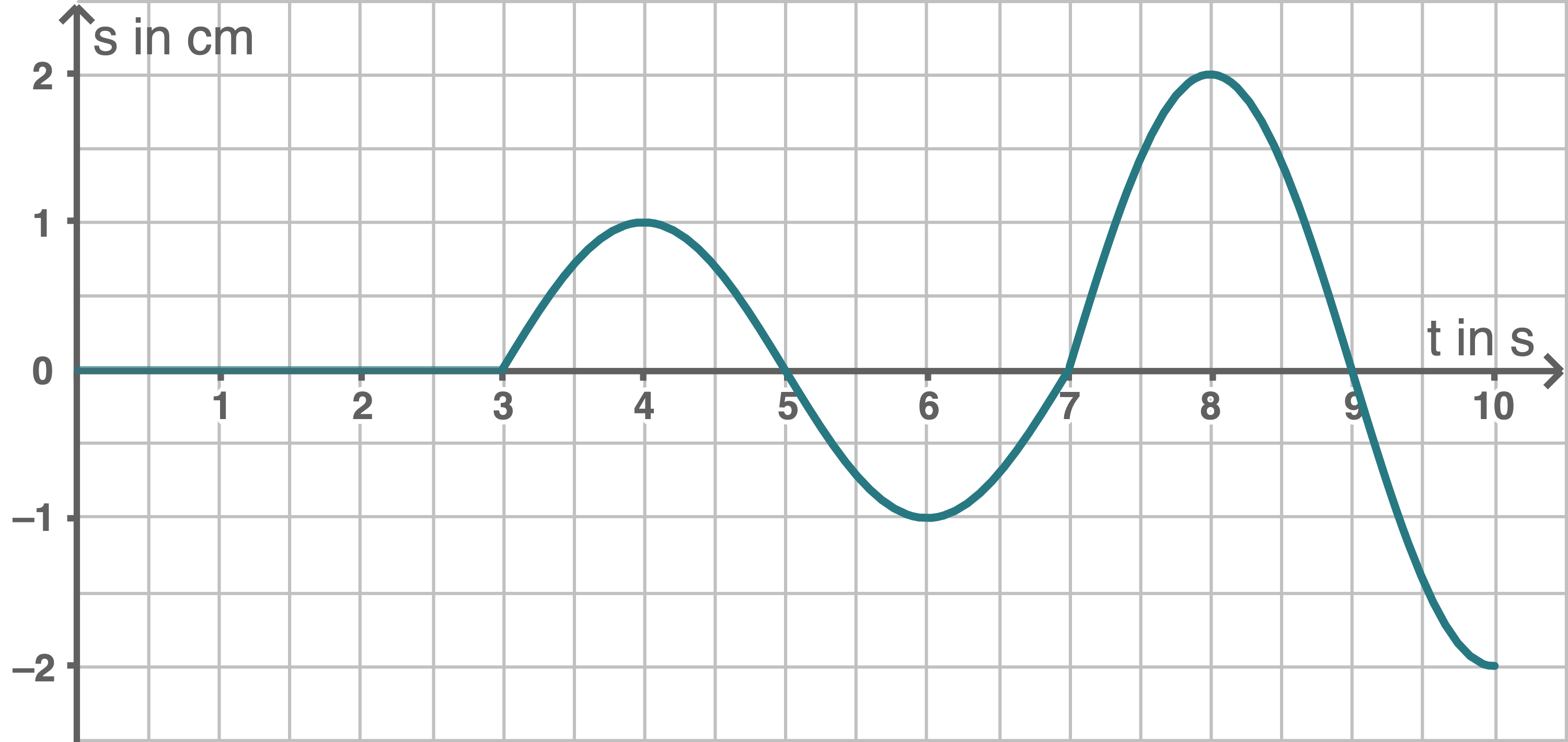
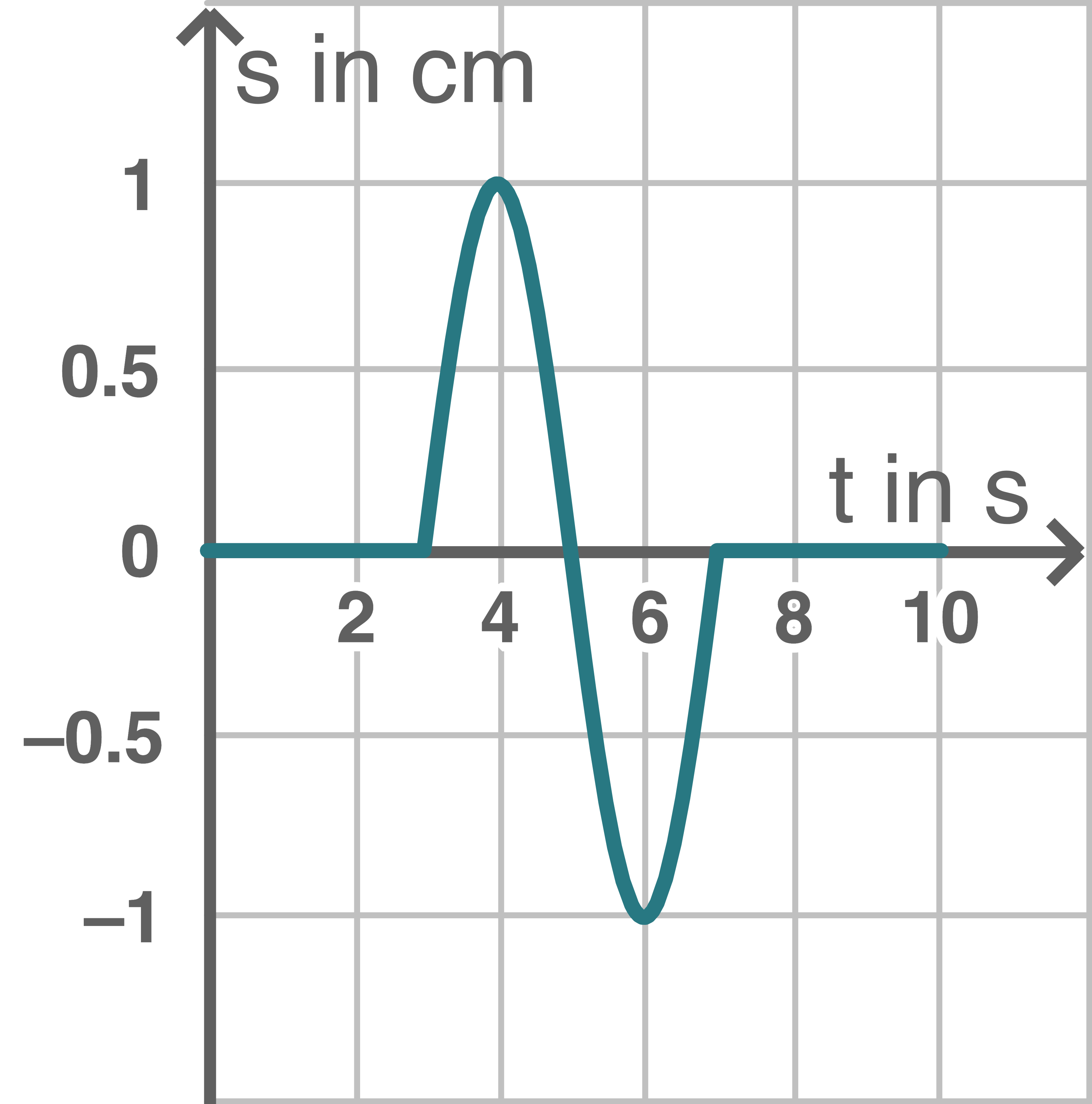
Abbildung 3 stellt die Bewegung eines Teilchens des Wellenträgers im Zeitraum 
Abbildung 3
d)
Erkläre, wie die unterschiedlichen Abschnitte des Schaubilds zustande kommen und bestimme den Ort des Teilchens.
In einem neuen Versuch starten beide Erreger zum Zeitpunkt
e)
Zeichne das Zeit-Auslenkung-Diagramm für das Zeitintervall  des Teilchens, das
des Teilchens, das  vom linken Ende entfernt ist.
vom linken Ende entfernt ist.
(12 VP)
1
a)
Die Amplitude entspricht der maximalen Auslenkung in eine Richtung und ist aus der Abbildung ablesbar mit 
b)
Es gilt  Umstellen nach
Umstellen nach  und einsetzen der Werte ergibt:
und einsetzen der Werte ergibt:
![\(\begin{array}[t]{rll}
E_{kin_{max}} &=& \dfrac{1}{2}\cdot m \cdot {v_{max}}^2&\quad \scriptsize \mid\;\cdot \dfrac{2}{m} \\[5pt]
\dfrac{2\cdot E_{kin_{max}}}{m}&=& {v_{max}}^2 \\[5pt]
{v_{max}}^2 &=& \dfrac{2\cdot E_{kin_{max}}}{m} &\quad \scriptsize \mid\; \sqrt{} \\[5pt]
{v_{max}} &=& \sqrt{\dfrac{2\cdot E_{kin_{max}}}{m}} \\[5pt]
{v_{max}} &=& \sqrt{\dfrac{2\cdot 8 }{2}}\;\frac{\;\text{m}}{\;\text{s}} \\[5pt]
&=& 2,6 \;\frac{\text{m}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/c4b08df169812642be693b6e597d601f803eeeb7d1a72afedc0a958ad317b39b_light.svg)
c)
1. Kinetische Energie für  bestimmen
Es gilt
bestimmen
Es gilt  Halbiert sich die Maximalgeschwindigkeit, so folgt:
Halbiert sich die Maximalgeschwindigkeit, so folgt:
![\(\begin{array}[t]{rll}
E_{kin_{neu}} &=&\dfrac{1}{2}\cdot m \cdot \left(\dfrac{1}{2}\cdot {v_{max}}\right)^2 \\[5pt]
&=&\dfrac{1}{2}\cdot m \cdot \dfrac{1}{4}\cdot {v_{max}}^2 \\[5pt]
&=& \dfrac{1}{4}\cdot \dfrac{1}{2}\cdot m \cdot {v_{max}}^2 \\[5pt]
&=& \dfrac{1}{4}\cdot E_{kin_{max}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ee5f8b2721d8947652bf6444b982c32fdbca34d837727e10ef1712921b78254c_light.svg) Einsetzen der Werte ergibt:
Einsetzen der Werte ergibt:
![\(\begin{array}[t]{rll}
E_{kin_{neu}}&=&\dfrac{1}{4}\cdot 8\;\text{J} \\[5pt]
&=& 2\;\text{J}
\end{array}\)](https://www.schullv.de/resources/formulas/58ac838a3fcd1735609393e6269d1c1dcfa791a84b1bf2404d21365b6ce08eab_light.svg) 2. Die Auslenkung
2. Die Auslenkung  aus dem Graphen ablesen
Der Betrag der Geschwindigkeit ist
aus dem Graphen ablesen
Der Betrag der Geschwindigkeit ist  bei den Auslenkungen
bei den Auslenkungen  und bei
und bei 
d)
Die Spannenergie ist durch  gegeben.
Umstellen nach
gegeben.
Umstellen nach  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
E_{\text{Spann}}&=& \dfrac{1}{2}\cdot D\cdot s^2&\quad \scriptsize \mid\;\cdot 2 \;\mid\; :s^2 \\[5pt]
\dfrac{2\cdot E_{\text{Spann}}}{s^2}&=& D \\[5pt]
D&=& \dfrac{2\cdot E_{\text{Spann}}}{s^2}
\end{array}\)](https://www.schullv.de/resources/formulas/dc938424d3d0cf6cfeebc39b9bd3a1bf3aac9513763c17e39fb9ea418d36cab9_light.svg) Die Spannenergie ist maximal bei maximaler Auslenkung, d.h. bei
Die Spannenergie ist maximal bei maximaler Auslenkung, d.h. bei  und
und  Einsetzen ergibt:
Einsetzen ergibt:
![\(\begin{array}[t]{rll}
D &=& \dfrac{2\cdot 8 \;\text{J}}{\left(0,6\text{m}\right)^2} &\quad \scriptsize \\[5pt]
D &=& \dfrac{2\cdot 8 \; \text{Nm}}{\left(0,6\text{m}\right)^2} &\quad \scriptsize \\[5pt]
D &\approx& 44\; \frac{\text{N}}{\text{m}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c9f97df239114068a83c4559067b51897701cc88bd78dffa32d5aa82de3f59e2_light.svg)
e)
Die Spannenergie ist minimal, wenn die Feder entspannt ist. Das ist der Fall, wenn sie in keine Richtung ausgelenkt ist.
Je stärker die Feder ausgelenkt ist, desto höher die Spannenergie.
Bei maximaler Auslenkung  und bei
und bei  ist die Spannenergie maximal.
Aus diesen drei Koordinaten ergibt sich die nach unten geöffnete Parabel für die Spannenergie.
ist die Spannenergie maximal.
Aus diesen drei Koordinaten ergibt sich die nach unten geöffnete Parabel für die Spannenergie.
 -
- -Diagramm
-Diagramm

2
a)
Die Wertetabelle wird erweitert zu:
Damit folgt das Diagramm:
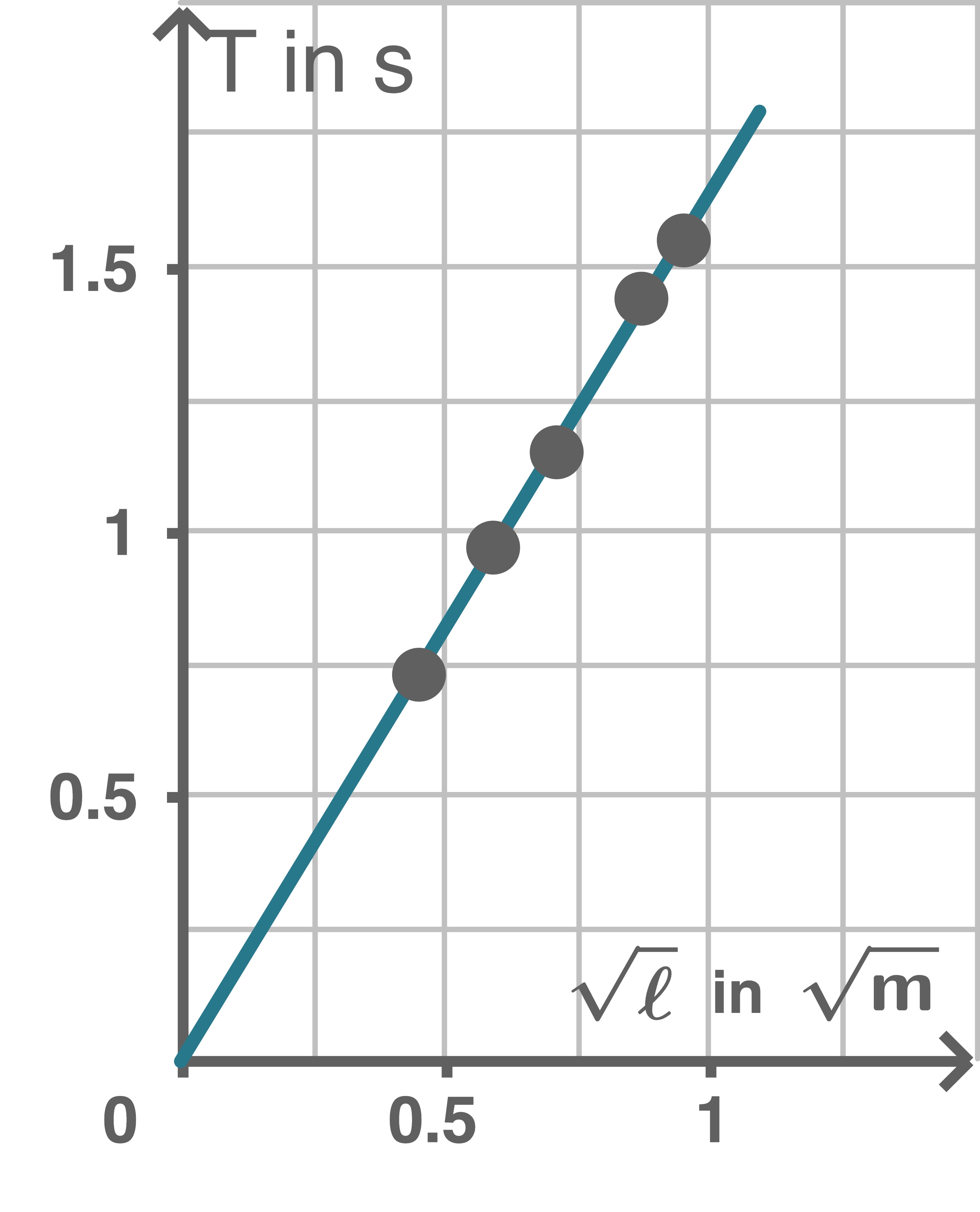 Der Graph entspricht einer Urspungsgeraden. Somit ist die Vermutung bestätigt.
Der Graph entspricht einer Urspungsgeraden. Somit ist die Vermutung bestätigt.
| Länge |
Dauer |
Periodendauer |
|
|---|---|---|---|
| 0,20 | 0,447 | 7,3 | 0,73 |
| 0,35 | 0,592 | 9,7 | 0,97 |
| 0,50 | 0,707 | 11,5 | 1,15 |
| 0,75 | 0,866 | 14,4 | 1,44 |
| 0,90 | 0,95 | 15,5 | 1,55 |

b)
Die Gleichung der Ausgleichsgeraden lässt sich aufstellen zu:
 Konstante k bestimmen
Konstante k bestimmen
![\(\begin{array}[t]{rll}
\text{Steigung} &\hat{=}& \frac{1,25\,\text{s}}{0,725\,\sqrt{\text{m}}} &\quad \scriptsize \\[5pt]
&\approx& 1,67 \;\frac{\text{s}}{\sqrt{\text{m}}}
\end{array}\)](https://www.schullv.de/resources/formulas/ecc93bfeced79b0ba7349824fd7e9535686323391fb5f7e1b139773b0adb34b7_light.svg) Damit gilt für die Periodendauer
Damit gilt für die Periodendauer 
c)
3
a)
Die Geschwindigkeit  , mit welcher sich die Welle von den Erregern ausgehend bewegen, ist:
, mit welcher sich die Welle von den Erregern ausgehend bewegen, ist:
![\(\begin{array}[t]{rll}
v&=& \frac{s}{t} &\quad \scriptsize \\[5pt]
&=& \frac{0,5\; \text{m}}{5,0\; \text{s}} &\quad \scriptsize \\[5pt]
&=& 0,1 \frac{\text{m}}{\text{s}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d5003b485d3fcf943bce6cf85252b60f875a9f013667846c97149c4d6cbef754_light.svg) Für die Wellenlänge gilt:
Für die Wellenlänge gilt:
![\(\begin{array}[t]{rll}
\lambda &=& \frac{v}{f} &\quad \scriptsize \\[5pt]
&=& \dfrac{0,1 \frac{\text{m}}{\text{s}}}{0,25 \text{Hz}} &\quad \scriptsize \\[5pt]
&=& 0,4\dfrac{\frac{\text{m}}{\text{s}}}{\frac{1}{\text{s}}} &\quad \scriptsize \\[5pt]
&=& 0,4\frac{\text{m}}{\text{s}} \cdot \text{s} &\quad \scriptsize \\[5pt]
&=& 0,40 \, \text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/f3c4b19ae528fa67292c5ecd89648bc7e4ee9167d3a545bb35fa9d3f4a3d1af8_light.svg)
b)
Die beiden Erreger werden um die Strecke der Amplitude ausgelenkt. Sie bewegen sich nur in  -Richtung, nicht in
-Richtung, nicht in  -Richtung.
-Richtung.
Da die Wellen eine Wellenlänge von m haben, treffen sie bei
m haben, treffen sie bei  m mit einer jeweils maximal ausgelenkten Amplitude aufeinander. Die von links kommende Welle ist dabei maximal nach unten ausgelenkt. Die von rechts kommende Welle maximal nach oben. Die Amplituden der Wellen addieren sich zu null. Die Wellen löschen sich aus.
m mit einer jeweils maximal ausgelenkten Amplitude aufeinander. Die von links kommende Welle ist dabei maximal nach unten ausgelenkt. Die von rechts kommende Welle maximal nach oben. Die Amplituden der Wellen addieren sich zu null. Die Wellen löschen sich aus.
Die Mitte verlässt ihre anfängliche Ruhelage somit zu keinem Zeitpunkt.
Da die Wellen eine Wellenlänge von
Die Mitte verlässt ihre anfängliche Ruhelage somit zu keinem Zeitpunkt.
c)
Die Wellen sind bei  noch nicht an den gegenüberliegenden Seiten angekommen. Sie befinden sich jeweils
noch nicht an den gegenüberliegenden Seiten angekommen. Sie befinden sich jeweils  von den Enden entfernt. Damit befinden sich die Wellen auf den Streckenabschnitten von
von den Enden entfernt. Damit befinden sich die Wellen auf den Streckenabschnitten von  bis
bis  bei
bei  in Ruhe. Sie sind im Umkehrpunkt ihrer Schwingung.
in Ruhe. Sie sind im Umkehrpunkt ihrer Schwingung.
Die Punkte bei m und bei
m und bei  m befinden sich ebenfalls in Ruhe.
Zu Zeitpunkt
m befinden sich ebenfalls in Ruhe.
Zu Zeitpunkt  haben die Wellen 2,5 Wellenlängen zurückgelegt.
Damit resultiert näherungsweise folgendes Momentanbild des Wellenträgers:
haben die Wellen 2,5 Wellenlängen zurückgelegt.
Damit resultiert näherungsweise folgendes Momentanbild des Wellenträgers:
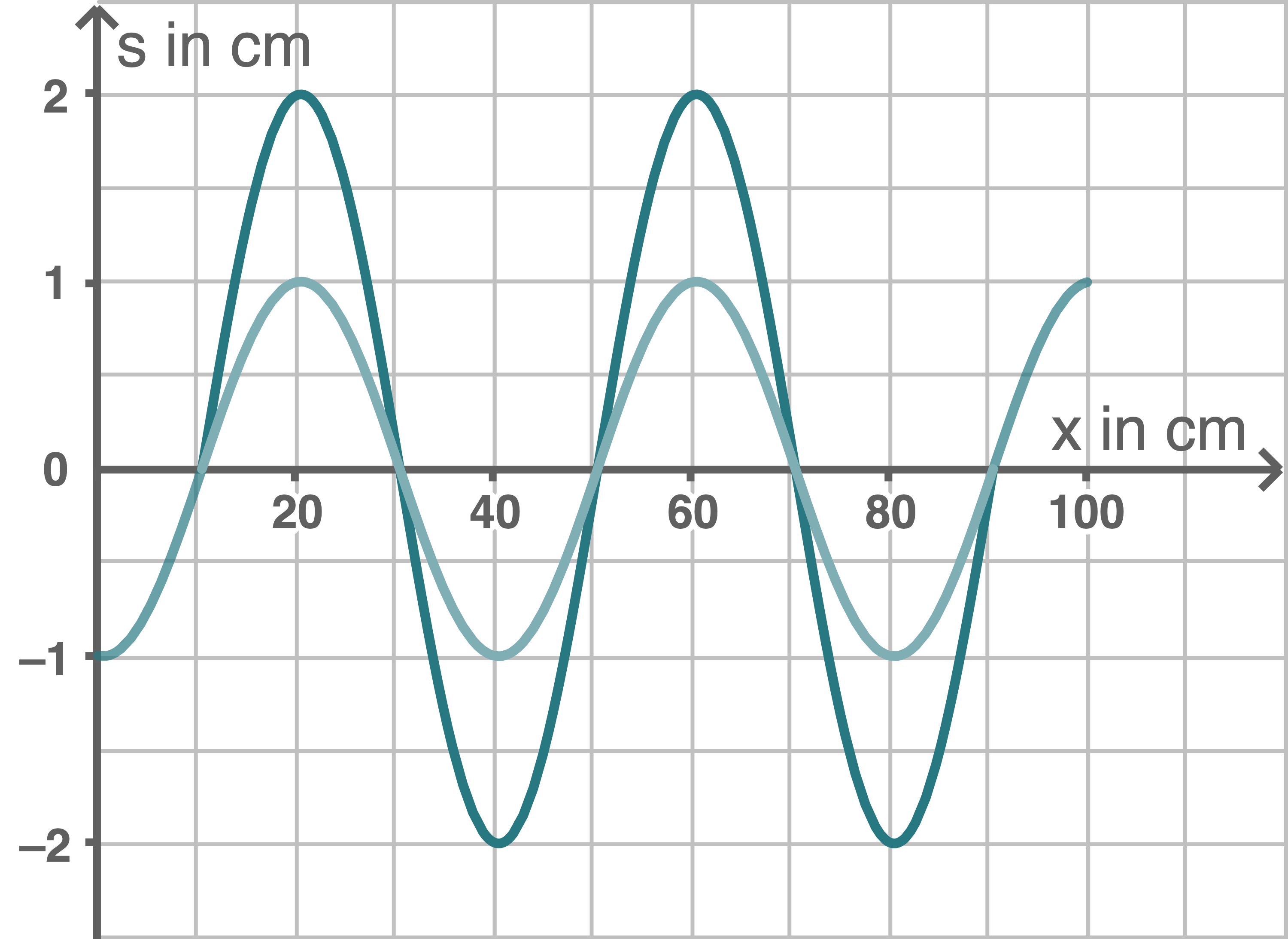
Die Punkte bei

d)
Beschreibung des Schaubilds
Bei  ändert sich der Ort des Teilchens nicht. Hier ist
ändert sich der Ort des Teilchens nicht. Hier ist  Bis
Bis  befindet sich das Teilchen in seiner Gleichgewichtslage. Die Welle von
befindet sich das Teilchen in seiner Gleichgewichtslage. Die Welle von  kommt an.
Nach
kommt an.
Nach  wird das Teilchen nach oben ausgelenkt, bis es sich bei
wird das Teilchen nach oben ausgelenkt, bis es sich bei  an seinem höchsten Punkt befindet.
Bei
an seinem höchsten Punkt befindet.
Bei  passiert das Teilchen die Gleichgewichtslage um schließlich nach
passiert das Teilchen die Gleichgewichtslage um schließlich nach  \;\text{s} seinen tiefsten Punkt zu durchlaufen.
Nach
\;\text{s} seinen tiefsten Punkt zu durchlaufen.
Nach  durchläuft das Teilchen die Gleichgewichtslage erneut und hört auf zu schwingen, bleibt also in Ruhe.
Die Welle von
durchläuft das Teilchen die Gleichgewichtslage erneut und hört auf zu schwingen, bleibt also in Ruhe.
Die Welle von  kommt an, beide Wellen treffen gleichphasig aufeinander und heben sich auf.
Ort des Teilchens bestimmen
Da das Teilchen erst nach
kommt an, beide Wellen treffen gleichphasig aufeinander und heben sich auf.
Ort des Teilchens bestimmen
Da das Teilchen erst nach  maximal nach oben ausgelenkt ist, braucht die Welle vom rechten Erreger bis zum Ort des Teilchens
maximal nach oben ausgelenkt ist, braucht die Welle vom rechten Erreger bis zum Ort des Teilchens  s.
s.
![\(\begin{array}[t]{rll}
s&=& v \cdot t &\quad \scriptsize \\[5pt]
&=& 0,1 \,\frac{\text{m}}{\text{s}} \cdot 3 \,\text{s} &\quad \scriptsize \\[5pt]
&=& 0,3\,\text{m} &\quad \scriptsize \\[5pt]
&=& 30\, \text{cm} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fd6c6ceec29c70fad6294e6c5a903e9ff182af9a4a079d26cd4cc6fa1ac5dc9c_light.svg)
Das Teilchen befindet sich cm links vom rechten Erreger.
cm links vom rechten Erreger.
Das Teilchen befindet sich
e)
Die Welle ausgelöst von Erreger  kommt nach
kommt nach  an. Die Bewegung der Welle wird eine Periodendauer ausgeführt. Zum Zeitpunkt
an. Die Bewegung der Welle wird eine Periodendauer ausgeführt. Zum Zeitpunkt  kommt die Welle von
kommt die Welle von  an.
Die Amplituden überlagern sich aufgrund der gleichphasigen Schwingung, das Teilchen wird doppelt so stark ausgelenkt.
an.
Die Amplituden überlagern sich aufgrund der gleichphasigen Schwingung, das Teilchen wird doppelt so stark ausgelenkt.