Aufgabe 2 – Licht
1.
Das Licht eines Laserpointers der Wellenlänge  fällt senkrecht auf einen Doppelspalt. Parallel zum Doppelspalt befindet sich im Abstand von
fällt senkrecht auf einen Doppelspalt. Parallel zum Doppelspalt befindet sich im Abstand von  ein Schirm. Auf diesem ist ein Streifenmuster erkennbar.
ein Schirm. Auf diesem ist ein Streifenmuster erkennbar.


a)
Erkläre das Zustandekommen des Streifenmusters.
Das Maximum 3. Ordnung hat vom Maximum 0. Ordnung einen Abstand von
b)
Zeige, dass der Spaltmittenabstand  beträgt.
beträgt.
Die Spaltbreite der beiden Spalte beträgt jeweils
c)
Erkläre, warum einige Doppelspaltmaxima nicht beobachtbar sind.
d)
Berechne Lage und Ordnung des ersten nicht beobachtbaren Doppelspaltmaximums auf dem Schirm.
e)
Erkläre, wie sich eine Verdoppelung des Spaltmittenabstandes bei konstanter Spaltbreite auf das lnterferenzbild auswirkt.
(12 VP)
2.
In drei Experimenten wird ein Gitter mit der Gitterkonstanten  nacheinander mit Laserlicht senkrecht beleuchtet. Parallel zum Gitter befindet sich in einem festen Abstand von
nacheinander mit Laserlicht senkrecht beleuchtet. Parallel zum Gitter befindet sich in einem festen Abstand von  ein Schirm.
ein Schirm.
Für die drei Experimente können die Wellenlänge des Lasers und die Anzahl der beleuchteten Spalte unabhängig voneinander variiert werden.
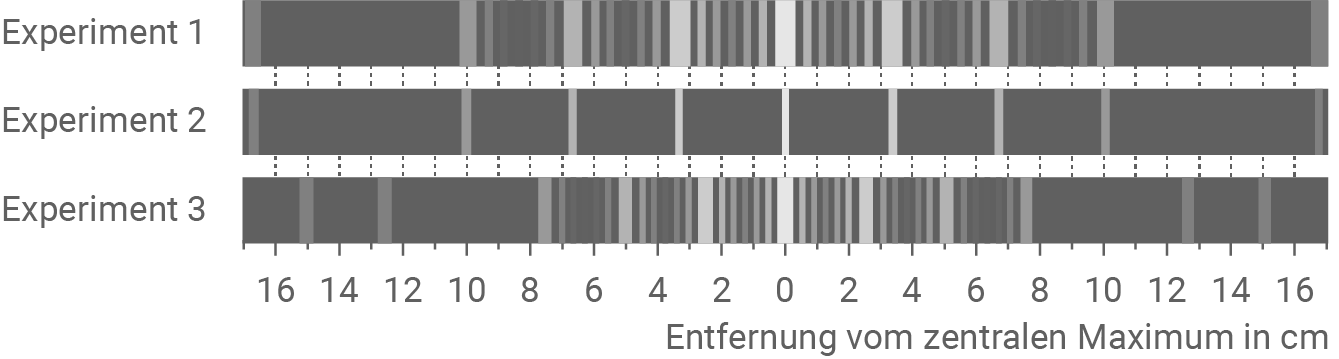
Man erhält die in Abbildung 1 dargestellten Helligkeitsverteilungen. In den Experimenten 1 und 3 erkennt man zwischen zwei Hauptmaxima 5 Nebenmaxima. In Experiment 2 sind keine Nebenmaxima zu beobachten.
Für die drei Experimente können die Wellenlänge des Lasers und die Anzahl der beleuchteten Spalte unabhängig voneinander variiert werden.
Man erhält die in Abbildung 1 dargestellten Helligkeitsverteilungen. In den Experimenten 1 und 3 erkennt man zwischen zwei Hauptmaxima 5 Nebenmaxima. In Experiment 2 sind keine Nebenmaxima zu beobachten.

Abbildung 1
a)
Gib an, wie viele unterschiedliche Wellenlängen in den drei Experimenten verwendet wurden und begründe deine Antwort.
b)
Berechne die Wellenlängen der verwendeten Laser.
c)
Vergleiche die Experimente hinsichtlich der Anzahl der beleuchteten Spalte und begründe deine Antwort.
Mit dem Laser aus Experiment 1 werden in einem weiteren Experiment nun 3 Spalte ausgeleuchtet. Das entstehende Beugungsbild wird mit dem aus Experiment 1 verglichen.
d)
Beschreibe zwei Unterschiede der Beugungsbilder.
(8 VP)
3.
In einem Experiment wird Licht der Wellenlänge  auf eine Fotozelle gerichtet. Die Ablöseenergie beträgt bei dieser Fotozelle
auf eine Fotozelle gerichtet. Die Ablöseenergie beträgt bei dieser Fotozelle 
 bis zu einem konstanten Endwert ansteigt.
bis zu einem konstanten Endwert ansteigt.
a)
Skizziere und beschrifte den schematischen Aufbau einer Fotozelle.
b)
Bestätige durch eine Rechnung, dass das verwendete Licht Elektronen aus dem Kathodenmaterial der Fotozelle auslöst.
Misst man die Spannung zwischen Anode und Kathode, so stellt man fest, dass nach dem Einschalten der Lichtquelle die Spannung von
c)
Erkläre diese Beobachtung.
In einem neuen Versuch wird ein höherer Endwert der Spannung erreicht.
d)
Erkläre, ob eine Veränderung der Intensität oder der Wellenlänge des Lichts diesen Effekt bewirken kann.
(10 VP)
1
a)
Die Entstehung des Interferenzbildes auf dem Schirm erfolgt aufgrund der Beugung des monochromatischen Lichts an den beiden schmalen Spalten im Doppelspalt.
Wenn Licht auf die Spalte trifft, werden die einzelnen Spalte zu neuen Quellen von Elementarwellen, die sich in alle Richtungen ausbreiten. Diese Elementarwellen überlagern sich auf dem Schirm, und an bestimmten Stellen interferieren sie konstruktiv, was zu hellen Streifen führt, während an anderen Stellen destruktive Interferenz auftritt, was zu dunklen Streifen führt.
Das resultierende Interferenzmuster auf dem Schirm besteht aus abwechselnd hellen und dunklen Streifen und wird als Interferenzbild bezeichnet.
b)
Herleitung Kleinwinkelnäherung
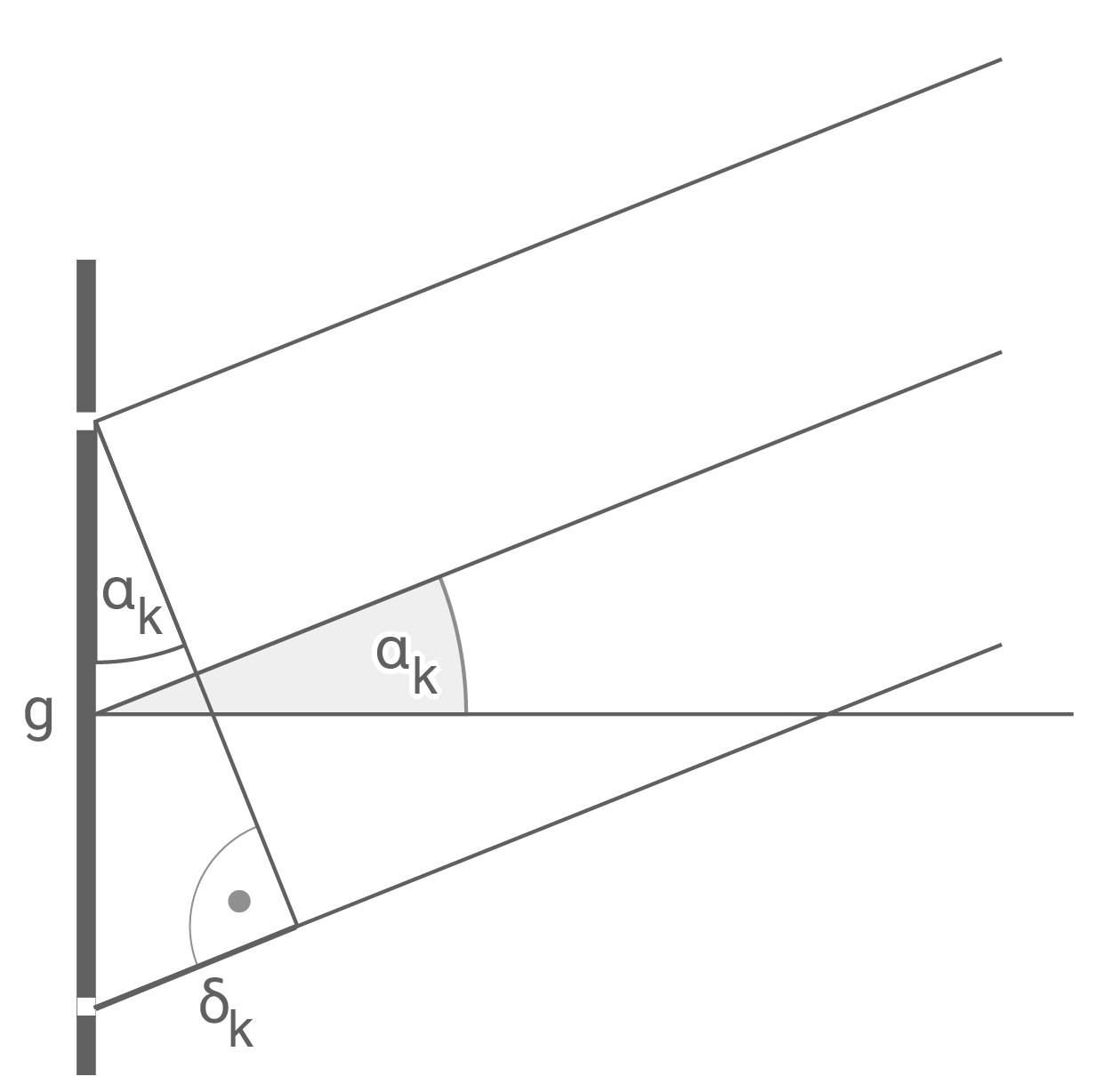 Es gilt:
Es gilt:  Für
Für  entstehen Intensitätsmaxima und für
entstehen Intensitätsmaxima und für  entstehen Intensitätsminima für
entstehen Intensitätsminima für  Für Winkel mit
Für Winkel mit  entstehen Maxima, die Minima liegen dazwischen.
entstehen Maxima, die Minima liegen dazwischen.
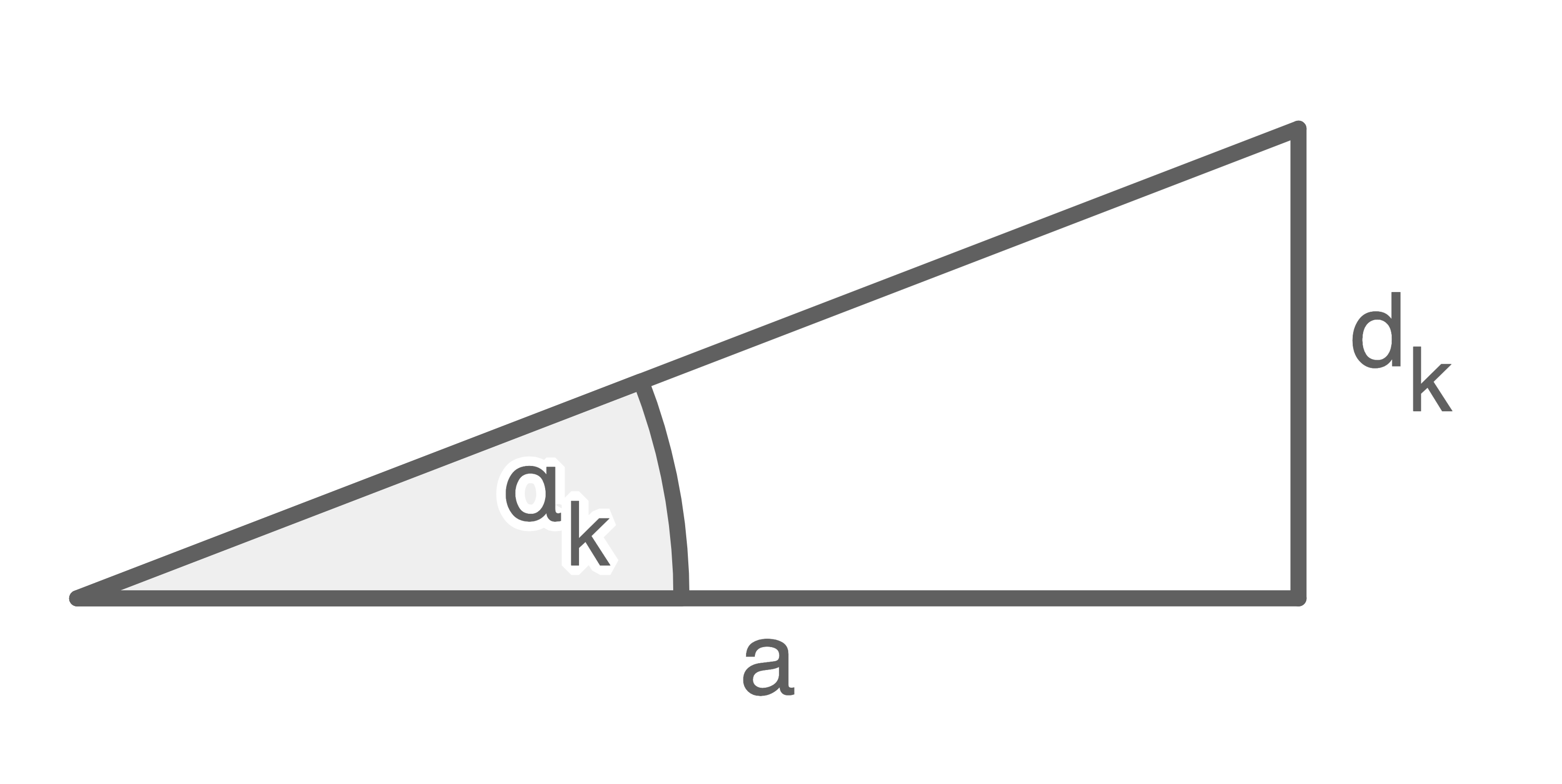 Für kleine Winkel
Für kleine Winkel  gilt:
gilt:
![\(\begin{array}[t]{rll}
\sin (\alpha_k)&=& \tan (\alpha_k) \\[5pt]
\dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a} &\quad \scriptsize \mid\;\cdot a \\[5pt]
\dfrac{k \cdot \lambda}{g}\cdot a&=& d_k \\[5pt]
d_k &=& k\cdot \dfrac{\lambda \cdot a}{g}
\end{array}\)](https://www.schullv.de/resources/formulas/87858f3f9e35ddb457143155293336c3527c8c1a93d2d53abc8e04464d03c5eb_light.svg) Spaltmittenabstand berechnen
Es wird die Kleinwinkelnäherung angewandt, da die Winkel klein sind.
Spaltmittenabstand berechnen
Es wird die Kleinwinkelnäherung angewandt, da die Winkel klein sind.
![\(\begin{array}[t]{rll}
d_k&=& \dfrac{k \cdot \lambda}{g}\cdot a &\quad \scriptsize \mid\;\cdot g \;\mid\;:d_k \\[5pt]
g&=& \dfrac{k \cdot \lambda\cdot a}{d_k}\\[5pt]
g&=& \dfrac{3 \cdot 630\cdot 10^{-9}\cdot 6,9}{0,026}\;\text{m} \\[5pt]
g&=& 5,0 \cdot 10^{-4} \;\text{m} \\[5pt]
g&=& 500 \;\mu\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/81e1bffbc00a124afea249f874cb71ee9d26d5626ccbe062f756e3ad17749ef2_light.svg)

Die Abstände  der Maxima vom Maximum 0. Ordnung lassen sich mit
der Maxima vom Maximum 0. Ordnung lassen sich mit  berechnen.
berechnen.  entspricht dem Abstand des Schirms zum Doppelspalt.
entspricht dem Abstand des Schirms zum Doppelspalt.

c)
Maxima und Minima entstehen bei der Beugung an den Einzelspalten. Wenn ein Doppelspaltmaximum an der Stelle eines Einzelspaltminimums liegt, fällt dieses weg, da von beiden Spalten keine Wellen ankommen, die miteinander interferieren können.
d)
Für die Winkel, bei denen die Einzelspaltminima liegen, gilt:
 für
für 
 entspricht der Spaltbreite.
Anwendung der Kleinwinkelnäherung:
entspricht der Spaltbreite.
Anwendung der Kleinwinkelnäherung:
![\(\begin{array}[t]{rll}
\dfrac{n\cdot \lambda}{b} &=& \dfrac{x_n}{a} &\quad \scriptsize \mid\;\cdot a \\[5pt]
\dfrac{n\cdot \lambda}{b}\cdot a&=& x_n \\[5pt]
x_n&=&\dfrac{n\cdot \lambda}{b}\cdot a
\end{array}\)](https://www.schullv.de/resources/formulas/e9b9f807224b9b8008e611e88a452da0b1454ea65027f6636625829e70a348e8_light.svg) Für
Für  ergeben sich die Abstände der Einzelspaltminima vom Maximum 0. Ordnung:
ergeben sich die Abstände der Einzelspaltminima vom Maximum 0. Ordnung:

 Der Spaltmittenabstand
Der Spaltmittenabstand  ist fünfmal so groß wie die Einzelspaltbreite
ist fünfmal so groß wie die Einzelspaltbreite  und somit fällt jedes fünfte Doppelspaltmaximum weg (außer dem Doppelspaltmaximum 0. Ordnung).
Das erste Maximum, das wegfällt, hat die fünfte Ordnung und liegt
und somit fällt jedes fünfte Doppelspaltmaximum weg (außer dem Doppelspaltmaximum 0. Ordnung).
Das erste Maximum, das wegfällt, hat die fünfte Ordnung und liegt  vom Maximum 0. Ordnung entfernt.
vom Maximum 0. Ordnung entfernt.
e)
Es gilt:  Für die Versopplung des Spaltmittenabstand
Für die Versopplung des Spaltmittenabstand  folgt:
folgt:
![\(\begin{array}[t]{rll}
d_{k_{neu}}&=&k\cdot \dfrac{\lambda \cdot a}{2\cdot g} \\[5pt]
&=&\dfrac{1}{2}\cdot k \cdot \dfrac{\lambda \cdot a}{g} \\[5pt]
&=& \dfrac{1}{2}\cdot d_k
\end{array}\)](https://www.schullv.de/resources/formulas/603778158c1e6eb6664eb61042bc33058a4e55e87c20abc10b2a96ed363ba7f8_light.svg) Wird der Spaltmittenabstand
Wird der Spaltmittenabstand  verdoppelt, so halbiert sich der Abstand
verdoppelt, so halbiert sich der Abstand  der Maxima vom Maximum 0. Ordnung.
Die Einzelspaltbreite bleicht gleich. Daraus folgt, dass die ausfallenden Maxima an denselben Stellen liegen und somit fällt jedes zehnte Maximum weg.
der Maxima vom Maximum 0. Ordnung.
Die Einzelspaltbreite bleicht gleich. Daraus folgt, dass die ausfallenden Maxima an denselben Stellen liegen und somit fällt jedes zehnte Maximum weg.
2
a)
In allen Experimenten kann die Kleinwinkelnäherung verwendet werden, da die Abstände der Maxima untereinander gleich sind.
Es gilt:  In den Experimenten 1 und 2 liegen die Maxima an den gleichen Stellen, weshalb die gleichen Wellenlängen verwendet wurden.
Im dritten Experiment liegen die Maxima näher beieinander, denn die Wellenlängen sind kleiner.
Es wurden also zwei verschiedene Wellenlängen verwendet.
In den Experimenten 1 und 2 liegen die Maxima an den gleichen Stellen, weshalb die gleichen Wellenlängen verwendet wurden.
Im dritten Experiment liegen die Maxima näher beieinander, denn die Wellenlängen sind kleiner.
Es wurden also zwei verschiedene Wellenlängen verwendet.
b)
Das Maximum 3. Ordnung lässt sich in den Experimenten 1 und 2 bei  ablesen.
ablesen.
![\(\begin{array}[t]{rll}
d_k&=&k\cdot \dfrac{\lambda \cdot a}{g} \\[5pt]
d_k \cdot g&=& k\cdot \lambda \cdot a \quad \scriptsize\mid\;:k:a \\[5pt]
\dfrac{d_k \cdot g}{k\cdot a}&=& \lambda \\[5pt]
\lambda_{1,2}&=&\dfrac{d_k \cdot g}{k\cdot a} \\[5pt]
\lambda_{1,2}&=&\dfrac{d_3 \cdot g}{3\cdot a} \\[5pt]
\lambda_{1,2}&=&\dfrac{0,100\cdot 200 \cdot 10^{-6}\;\text{m}}{3\cdot 10,0} \\[5pt]
\lambda_{1,2}&=& 670 \;\text{nm}
\end{array}\)](https://www.schullv.de/resources/formulas/418e0375df5fb140ef04ddfa3ab2fb14cb2a354e5298af6b0e7e8b5e480e04e0_light.svg) Das Maximum 2. Ordnung wird in Experiment 3 mit
Das Maximum 2. Ordnung wird in Experiment 3 mit  abgelesen.
abgelesen.
![\(\begin{array}[t]{rll}
\lambda_3&=&\dfrac{d_2 \cdot g}{2\cdot a} \\[5pt]
\lambda_3&=&\dfrac{0,050\cdot 200 \cdot 10^{-6}\;\text{m}}{2\cdot 10,0} \\[5pt]
\lambda_3&=& 500 \;\text{nm}
\end{array}\)](https://www.schullv.de/resources/formulas/af006f3759e95749e747f3ec9b32c6053a0e75b1426371b4eb46b7b14fb8b3c0_light.svg)
c)
In den Experimenten 1 und 3 können breite Hauptmaxima erkannt werden. Dazwischen liegen fünf Nebenmaxima, also wurden dabei sieben Spalte beleuchtet.
Im Experiment 2 sind scharfe Hauptmaxima sichtbar, jedoch keine Nebenmaxima. Es wurden folglich viele Spalte beleuchtet.
d)
Die Intensität nimmt aufgrund der geringeren Spaltzahl ab, wenn statt sieben Spalten nur noch drei beleuchtet werden.
Die Anzahl der Nebenmaxima beträgt deshalb eins.
(Die Intensitätsverteilung wird unschärfer.)
3
a)
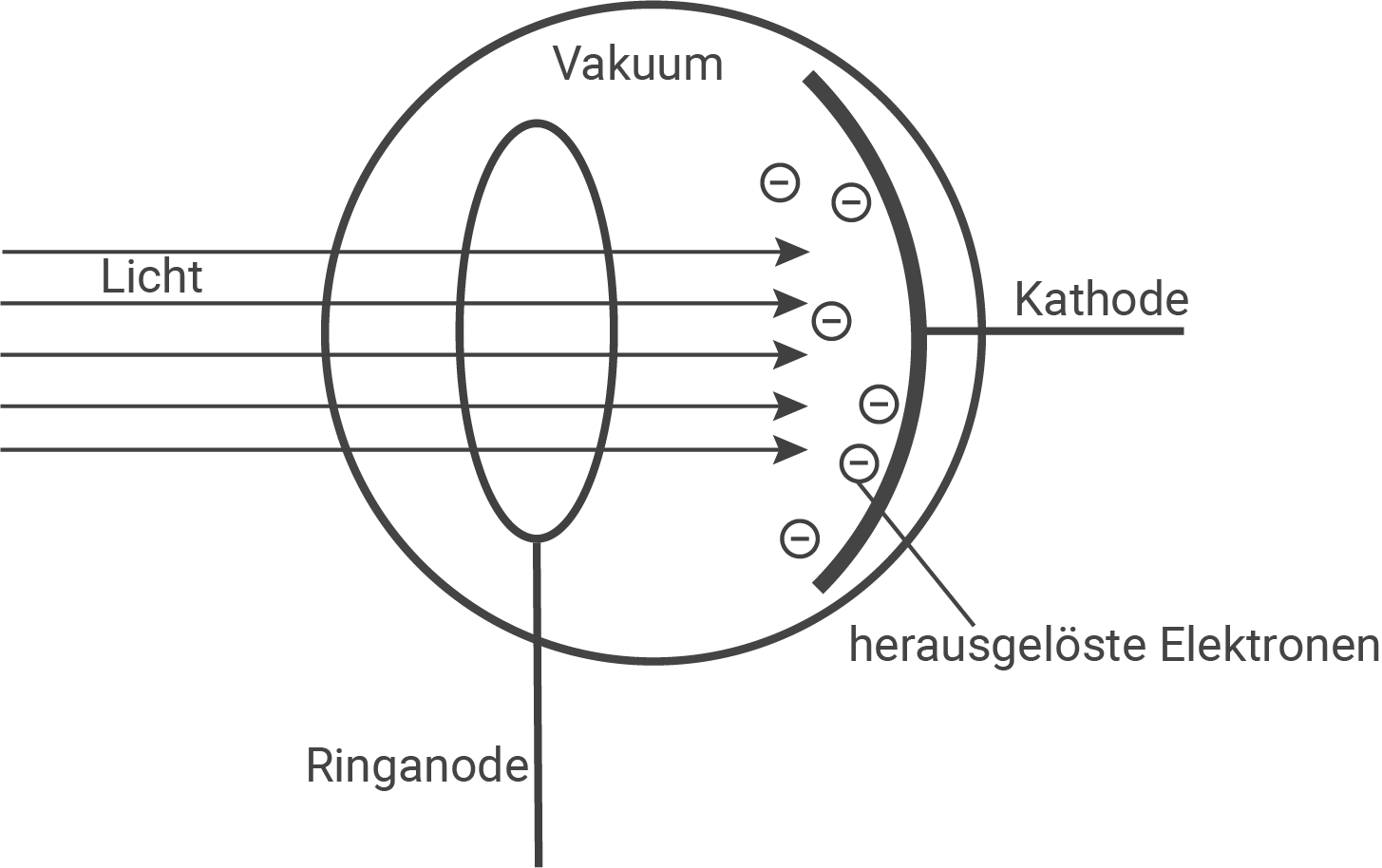
b)
Fotoeffekt: Die Energie des einfallenden Lichtes wird auf die Elektronen der Fotozellen übertragen.
Die Photonenenergie muss größer als die Ablöseenergie  die vom Kathodenmaterial abhängig ist, sein, um Elektronen aus der Kathode auszulösen.
die vom Kathodenmaterial abhängig ist, sein, um Elektronen aus der Kathode auszulösen.





 Somit folgt:
Somit folgt:  und es werden Elektronen aus der Kathode herausgelöst.
und es werden Elektronen aus der Kathode herausgelöst.
c)
Die herausgelösten Elektronen fliegen zur Anode und laden diese negativ auf. Zwischen Kathode und Anode entsteht folglich ein elektrisches Feld. Solange die Elektronen die Anode erreichen können, baut sich eine Gegenspannung  auf.
Wenn die Spannung genügend groß wird, nämlich so dass nur noch die energiereichsten Elektronen der Energie
auf.
Wenn die Spannung genügend groß wird, nämlich so dass nur noch die energiereichsten Elektronen der Energie  gerade noch so ankommen können, ist eine weitere Aufladung nicht mehr möglich und die erreichte Spannung bleibt konstant.
gerade noch so ankommen können, ist eine weitere Aufladung nicht mehr möglich und die erreichte Spannung bleibt konstant.
d)
Wird eine höhere Spannung erreicht, ist die Energie der energiereichsten Elektronen höher.
Die Änderung der Intensität hat keinen Einfluss auf den Spannungsendwert: Bei höherer Intensität würden in gleicher Zeit zwar mehr Photonen auf eine bestimmte Kathodenfläche treffen, womit mehr Elektronen ausgelöst würden. Die Maximalenergie dieser Elektronen würde dabei unverändert bleiben, denn die Energie der Photonen hängt nicht von der Intensität, sondern nur von der Frequenz des Lichts ab.
Die maximale Energie der Elektronen wurde durch eine höhere Frequenz oder eine kürzere Wellenlänge erhöht.