Aufgabe 2 – Licht
1.
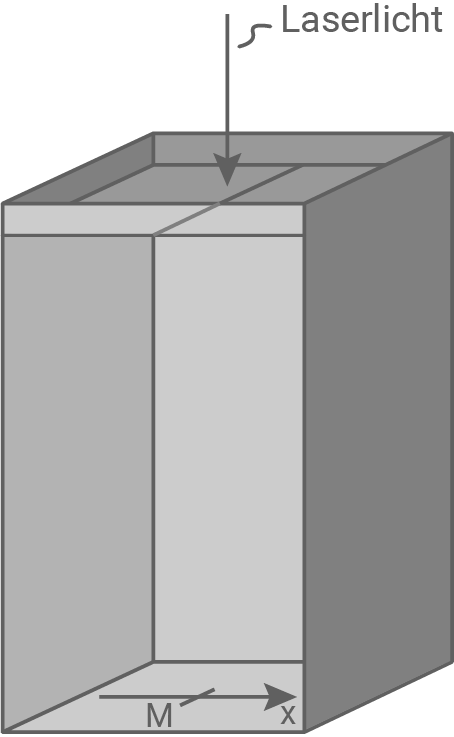
Abbildung 1 zeigt ein geschlossenes, quaderförmiges Gefäß, in dessen Deckplatte sich mittig ein Spalt befindet. Das Gefäß ist zunächst mit Luft gefüllt, der Abstand zwischen der Deckplatte und dem Boden beträgt  Die quadratische Bodenplatte besitzt die Kantenlänge
Die quadratische Bodenplatte besitzt die Kantenlänge  Laserlicht fällt senkrecht auf den Spalt. Dabei registriert man auf dem Boden des Gefäßes längs der
Laserlicht fällt senkrecht auf den Spalt. Dabei registriert man auf dem Boden des Gefäßes längs der  -Achse ein Interferenzmuster.
-Achse ein Interferenzmuster.
 -Achse bei Verwendung des oben beschriebenen Gefäßes. Danach wird das Gefäß vollständig mit Wasser gefüllt.
-Achse bei Verwendung des oben beschriebenen Gefäßes. Danach wird das Gefäß vollständig mit Wasser gefüllt.
Die Lichtgeschwindigkeit des grünen Laserlichts beträgt in Wasser 75 % der Vakuumlichtgeschwindigkeit. Durch geeignete Änderung der Spaltbreite wird erreicht, dass sich die Minima an den gleichen Stellen wie zuvor befinden.
a)
Erkläre mithilfe einer Skizze das Entstehen des Minimums erster Ordnung.
b)
Erläutere, wie sich der Abstand  des Minimums erster Ordnung von der Mitte
des Minimums erster Ordnung von der Mitte  der Bodenplatte berechnen lässt.
der Bodenplatte berechnen lässt.
Um die Breite des Spalts zu bestimmen, wird das Experiment nun nacheinander mit fünf verschiedenen Lasern durchgeführt. Die Tabelle zeigt für jeden Laser den Abstand  des Minimums erster Ordnung von
des Minimums erster Ordnung von 
| Farbe des Laserlichts | Wellenlänge in |
|
|---|---|---|
| violett | 405 | 6,5 |
| blau | 460 | 7,0 |
| grün | 532 | 8,5 |
| orange | 589 | 9,5 |
| rot | 650 | 11,0 |
Tabelle 1

Abbildung 1
c)
Bestimme unter Verwendung aller Messwerte die Breite des Spalts.
d)
Berechne die Anzahl der Intensitätsminima, die bei dieser Versuchsreihe maximal auf der Bodenplatte längs der  -Achse vorhanden sein können.
-Achse vorhanden sein können.
Im Folgenden wird nur mit dem grünen Laserlicht aus Tabelle experimentiert. Zunächst beobachtet man die Lage der Minima längs der Die Lichtgeschwindigkeit des grünen Laserlichts beträgt in Wasser 75 % der Vakuumlichtgeschwindigkeit. Durch geeignete Änderung der Spaltbreite wird erreicht, dass sich die Minima an den gleichen Stellen wie zuvor befinden.
e)
Berechne die dafür erforderliche Spaltbreite.
(12 VP)
2.
Das leere Gefäß aus der 1. Teilaufgabe erhält nun einen neuen Deckel mit einem Doppelspalt mit Spaltmittenabstand  und Spaltbreite
und Spaltbreite  (siehe Abbildung 2). Der Doppelspalt wird zunächst senkrecht mit dem grünen Laserlicht aus der Tabelle aus Aufgabe 1 beleuchtet. Dabei registriert man wieder auf dem Boden des Gefäßes längs der
(siehe Abbildung 2). Der Doppelspalt wird zunächst senkrecht mit dem grünen Laserlicht aus der Tabelle aus Aufgabe 1 beleuchtet. Dabei registriert man wieder auf dem Boden des Gefäßes längs der  -Achse ein Interferenzmuster.
-Achse ein Interferenzmuster.
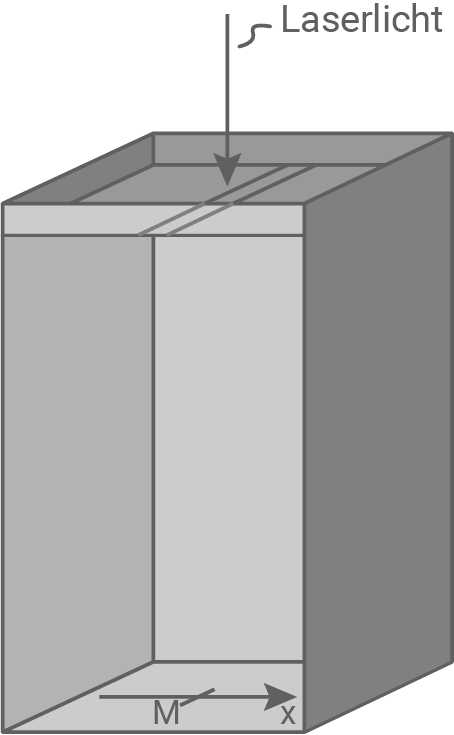
Abbildung 2
a)
Bestimme die Anzahl der Intensitätsmaxima, die auf der Bodenplatte längs der  -Achse vorhanden sind.
-Achse vorhanden sind.
Das Gefäß ist nun zur Hälfte mit Wasser gefüllt. An der Wasseroberfläche kommt es zur Lichtbrechung (siehe Abbildung 3). Abbildung 4 zeigt den Zusammenhang zwischen dem Einfallswinkel 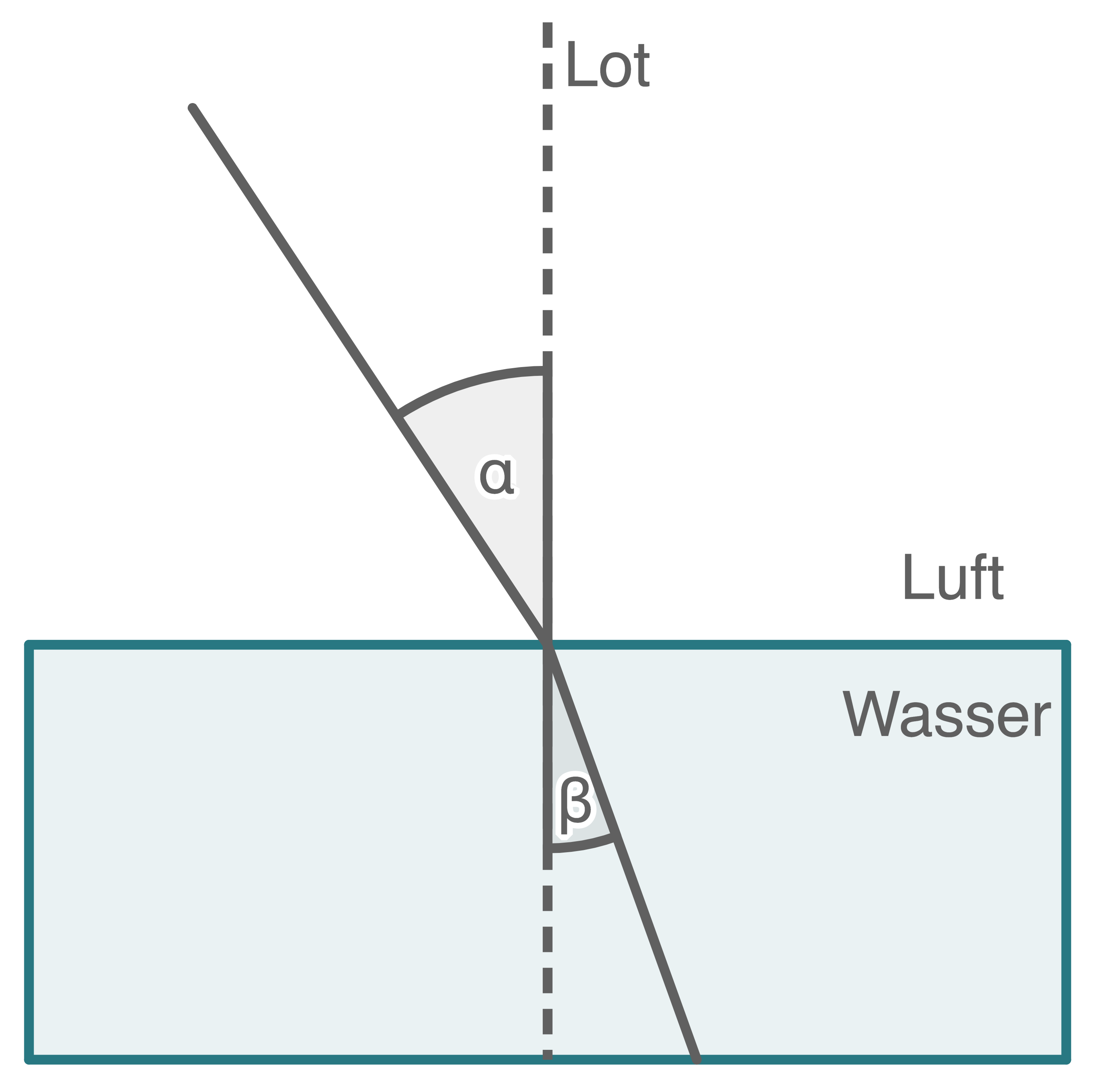
Abbildung 3

Abbildung 4
b)
Beschreibe, wie sich die Lage der Intensitätsmaxima durch die nun vorhandene Wasserfüllung verändert. Begründe deine Antwort.
c)
Bestimme, wie weit sich das Intentsitätsmaximum der 7. Ordnung verschoben hat.
(10 VP)
3.
Verschiedene positiv geladene Ionen mit vernachlässigbarer Anfangsgeschwindigkeit werden mittels einer Spannung von  beschleunigt. Anschließend treten sie senkrecht zu den Feldlinien eines homogenen Magnetfeldes der Flussdichte
beschleunigt. Anschließend treten sie senkrecht zu den Feldlinien eines homogenen Magnetfeldes der Flussdichte  ein. Dort werden die Bahnen der Ionen durch eine geeignete Messapparatur erfasst. Abbildung 5 zeigt Ausschnitte dieser Teilchenbahnen. Das Magnetfeld ist dabei senkrecht in die Abbildungsebene hinein gerichtet.
ein. Dort werden die Bahnen der Ionen durch eine geeignete Messapparatur erfasst. Abbildung 5 zeigt Ausschnitte dieser Teilchenbahnen. Das Magnetfeld ist dabei senkrecht in die Abbildungsebene hinein gerichtet.
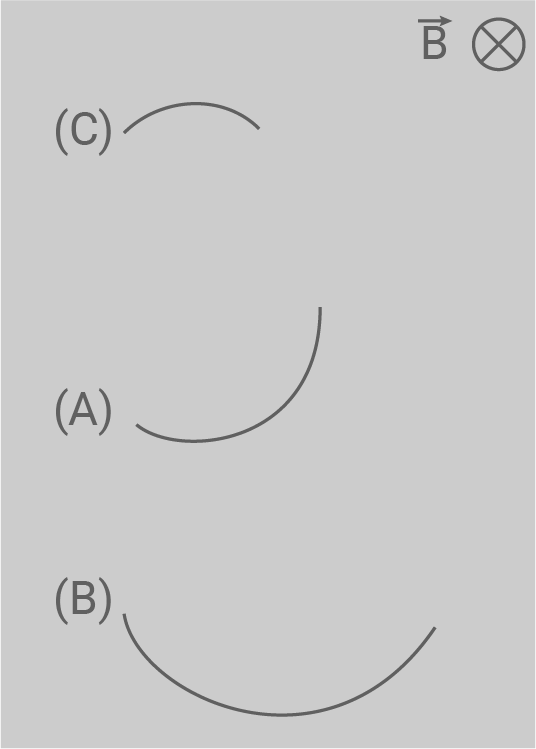
Abbildung 5
a)
Begründe, dass kreisförmige Bahnen zu erwarten sind.
b)
Erläutere, in welche Richtung sich ein Ion entlang der dargestellten Bahn (A) bewegt.
Der Betrag der für eine Kreisbahn notwendigen Zentripetalkraft
c)
Zeige, dass der Bahnradius proportional zur Geschwindigkeit des Ions ist.
Bei den positiv geladenen Ionen handelt es sich um die folgenden vier Sorten, wobei | Masse | Ladungsbetrag | |
|---|---|---|
Tabelle 2
d)
Zeige, dass der Radius von Bahn (A)  beträgt.
beträgt.
e)
Ordne die Bahnen (A), (B) und (C) den Ionensorten aus der Tabelle zu und begründe deine Antwort.
(8 VP)
1
a)
Das Laserlicht wird aufgrund des Huygenssches Prinzips an dem Einzelspalt gebeugt. Dieses besagt, dass jeder Punkt auf der Wellenfront als Ausgangspunkt einer Elementarwelle angesehen werden kann. Je nach Gangunterschied kommt es zu konstruktiver oder destruktiver Interferenz.
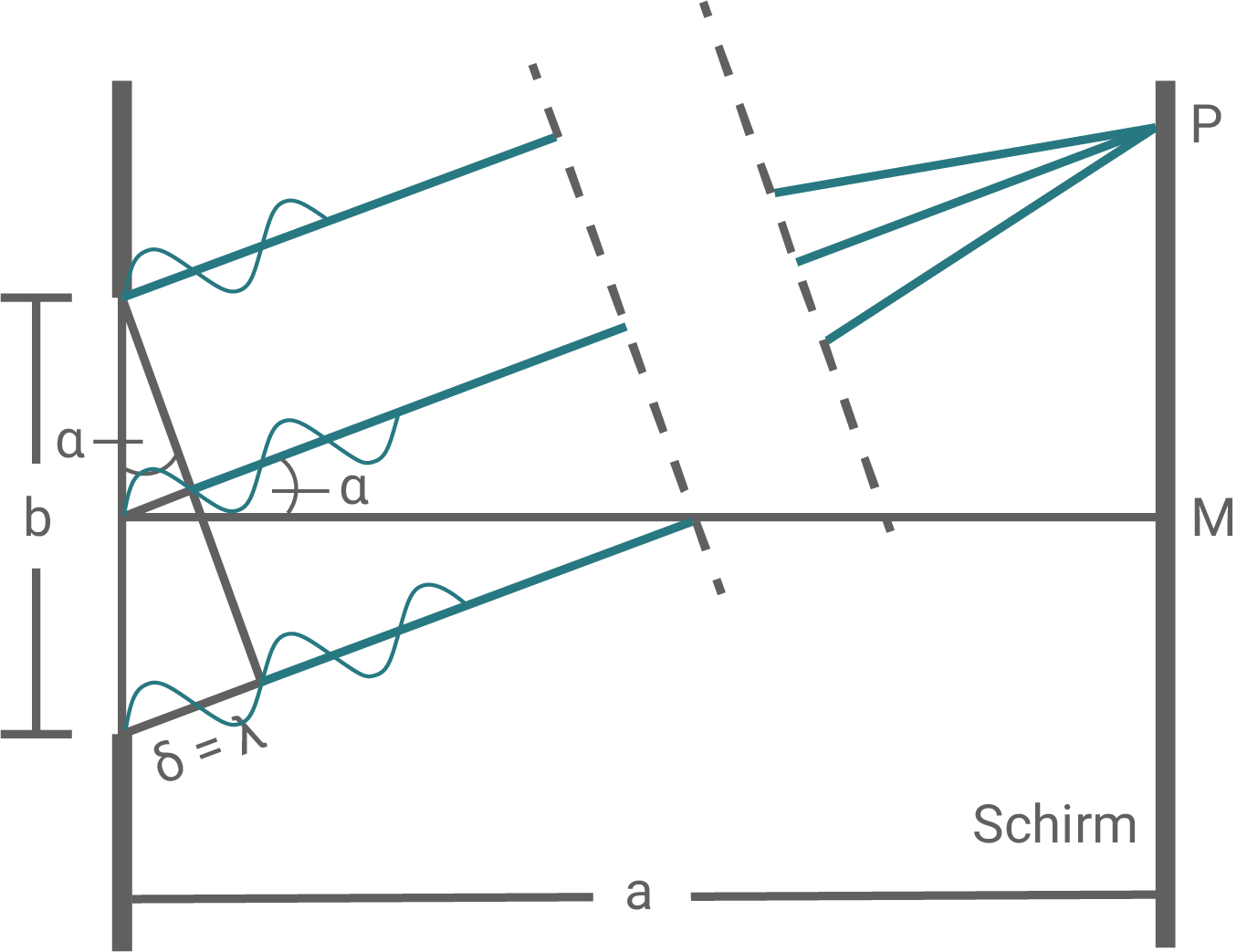 Die Wellenstrahlen, die vom Spalt ausgehen, werden zu parallelen Strahlen vereinfacht.
Der Gangunterschied
Die Wellenstrahlen, die vom Spalt ausgehen, werden zu parallelen Strahlen vereinfacht.
Der Gangunterschied  zwischen zwei Wellen, wird beschrieben durch:
zwischen zwei Wellen, wird beschrieben durch:
 Wenn
Wenn  löschen sich die Wellen gegenseitig aus, wodurch ein Minumum entsteht.
Für das Minimum erster Ordnung gilt:
löschen sich die Wellen gegenseitig aus, wodurch ein Minumum entsteht.
Für das Minimum erster Ordnung gilt:


b)
Die Abstände  der Minima vom Maximum 0. Ordnung lassen sich, wie der Skizze zu entnehmen, mit
der Minima vom Maximum 0. Ordnung lassen sich, wie der Skizze zu entnehmen, mit  mit
mit  berechnen.
berechnen.  entspricht dem Abstand des Schirms zum Doppelspalt.
entspricht dem Abstand des Schirms zum Doppelspalt.
c)
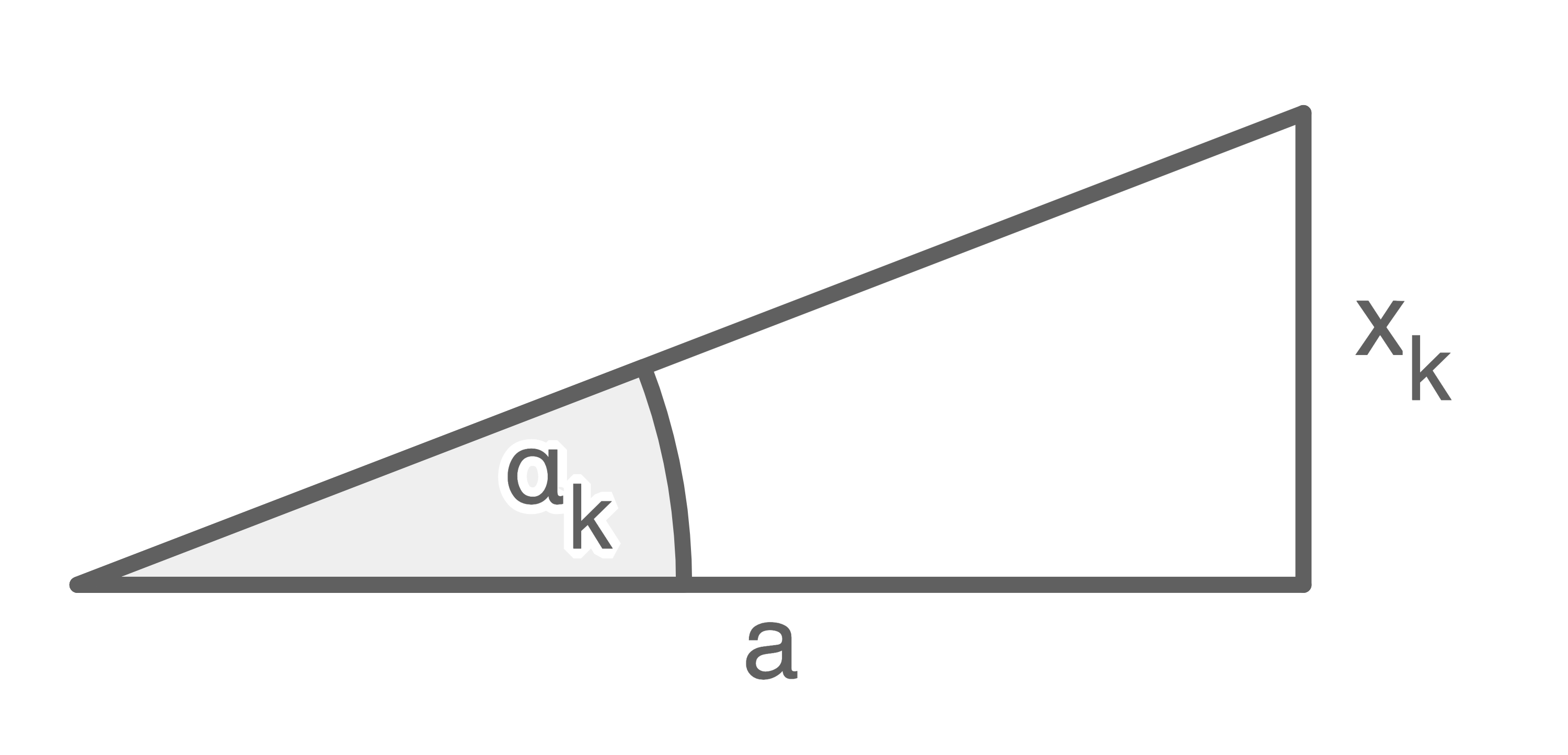
Da die Abstände der ersten Minima zur Mitte im Verglich zum Abstand der Bodenplatte zum Beugungsspalt sehr klein sind, darf die Kleinwinkelnährung angewandt werden. Es ergibt sich folgender Zusammenhang:
![\(\begin{array}[t]{rll}
\sin \alpha_1 &\approx& \tan \alpha_1 \\[5pt]
\dfrac{\lambda}{b}&\approx& \dfrac{x_1}{a} &\quad \scriptsize \mid\; \cdot b \\[5pt]
\lambda&\approx& \dfrac{x_1}{a} \cdot b &\quad \scriptsize \mid\; \cdot \dfrac{a}{x_1} \\[5pt]
\dfrac{\lambda \cdot a}{x_1}&\approx& b \\[5pt]
b &\approx& \dfrac{\lambda \cdot a}{x_1} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/86da860a91623934ee274720de1a3a585ab544c0ad998cc57fecbec0a3b16961_light.svg) Erweitern der Wertetabelle um die Spaltbreite
Erweitern der Wertetabelle um die Spaltbreite  ergibt:
ergibt:
Durch Berechnung des Mittelwerts der Spaltbreiten ergibt sich eine Spaltbreite von 
| Farbe des Laserlichts | Wellenlänge in |
||
|---|---|---|---|
| violett | 405 | 6,5 | 49,8 |
| blau | 460 | 7,0 | 52,6 |
| grün | 532 | 8,5 | 50,1 |
| orange | 589 | 9,5 | 49,6 |
| rot | 650 | 11,0 | 47,3 |
d)
Gegeben: 
 Gesucht:
Gesucht:  Lösung: Da die Bodenplatte
Lösung: Da die Bodenplatte  lang ist und somit der maximale Abstand eines Minimums
lang ist und somit der maximale Abstand eines Minimums  beträgt kann nun nicht mehr die Kleinwinkelnäherung angewandt werden, sondern die beiden Formeln müssen wie folgt einzeln ausgewertet werden:
1. Schritt: Berechnung des maximalen Winkels
beträgt kann nun nicht mehr die Kleinwinkelnäherung angewandt werden, sondern die beiden Formeln müssen wie folgt einzeln ausgewertet werden:
1. Schritt: Berechnung des maximalen Winkels  Der maximale Winkel wird wie folgt berechnet:
2. Schritt: Bestimmung der zu untersuchenden Wellenlänge
Ja kleiner die Wellenlänge ist, desto mehr Minima gibt es. Das violette Licht hat die kleinste Wellenlänge und verursacht somit die meisten Minima.
3. Schritt: Bestimmung des Zusammenhangs zwischen Winkel und der Anzahl des Minimas
Der Zusammenhang zwischen dem Winkel
Der maximale Winkel wird wie folgt berechnet:
2. Schritt: Bestimmung der zu untersuchenden Wellenlänge
Ja kleiner die Wellenlänge ist, desto mehr Minima gibt es. Das violette Licht hat die kleinste Wellenlänge und verursacht somit die meisten Minima.
3. Schritt: Bestimmung des Zusammenhangs zwischen Winkel und der Anzahl des Minimas
Der Zusammenhang zwischen dem Winkel  und der Anzahl des Minimas ist gegeben durch die folgende Formel:
und der Anzahl des Minimas ist gegeben durch die folgende Formel:
![\(\begin{array}[t]{rll}
\sin \alpha_{\text{k}} &=& \dfrac{k \cdot \lambda_{\text{viol}}}{b} &\quad \scriptsize \mid\; \cdot \dfrac{b}{\lambda_{\text{viol}}} \\[5pt]
\sin \alpha_{\text{k}} \cdot \dfrac{b}{\lambda_{\text{viol}}} &=& k
\end{array}\)](https://www.schullv.de/resources/formulas/91cf73c104204fed9210631e6e84a9dcb01cde6ed7137b81818fe2d171c5e9a8_light.svg) 4. Schritt: Bestimmung des Minimums höchster Ordnung
Der maximale Winkel
4. Schritt: Bestimmung des Minimums höchster Ordnung
Der maximale Winkel  beträgt
beträgt  Somit ist:
Somit ist:
![\(\begin{array}[t]{rll}
k&\le& \sin \alpha_{\text{max}} \cdot \dfrac{b}{\lambda_{\text{viol}}} \\[5pt]
k&\le& \sin 20,6^\circ \cdot \dfrac{49,9 \cdot 10^{-6} \text{ m}}{405 \cdot 10^{-9} \text{ m}} \\[5pt]
k&\le& 43,4
\end{array}\)](https://www.schullv.de/resources/formulas/9cc65ce8890007684f42b6fe4026cece2f49965d1d634d00e6a9afe245a8fcec_light.svg) 5. Schritt: Rückschluss auf die maximal Anzahl an Minima
Das Minimum höchster Ordung ist das Minima 43. Ordung. Somit gibt es auf jeder Seite 43 Minima, also 86 Minima insgesamt.
5. Schritt: Rückschluss auf die maximal Anzahl an Minima
Das Minimum höchster Ordung ist das Minima 43. Ordung. Somit gibt es auf jeder Seite 43 Minima, also 86 Minima insgesamt.
e)
Gegeben:  Gesucht:
Gesucht:  Lösung:
1. Schritt: Berechnung der Wellenlänge des grünen Lichts in Wasser
Lösung:
1. Schritt: Berechnung der Wellenlänge des grünen Lichts in Wasser
![\(\begin{array}[t]{rll}
c_{\text{w}} &=& 0,75 \cdot c &\quad \scriptsize \mid\; c=f \cdot \lambda \\[5pt]
f \cdot \lambda_{\text{w}}&=& 0,75 \cdot f \cdot \lambda &\quad \scriptsize \mid\ :f \\[5pt]
\lambda_{\text{w}}&=& 0,75 \cdot \lambda \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7f7f4c06668b772797bbc56e4805e7d49e9b8d7f231db9d9a52ef79b0b2e2cc6_light.svg) Hinweis: Beim Übergang einer Welle von einem Medium in das andere verändert sich die Wellenlänge, aber die Frequenz bleicht gleich.
2. Schritt: Berechnung der benötigten Spaltbreite
Damit die Minima an der gleichen Stelle auftreten muss gelten:
Hinweis: Beim Übergang einer Welle von einem Medium in das andere verändert sich die Wellenlänge, aber die Frequenz bleicht gleich.
2. Schritt: Berechnung der benötigten Spaltbreite
Damit die Minima an der gleichen Stelle auftreten muss gelten:
![\(\begin{array}[t]{rll}
\sin \alpha_{\text{k}} &=& \sin \alpha_{\text{k,w}} \\[5pt]
\dfrac{k \cdot \lambda}{b}&=&\dfrac{k \cdot \lambda_{\text{w}}}{b_{\text{w}}} &\quad \scriptsize \mid\; : k \\[5pt]
\dfrac{ \lambda}{b}&=&\dfrac{ \lambda_{\text{w}}}{b_{\text{w}}} &\quad \scriptsize \mid\; \cdot \dfrac{b_{\text{w}} \cdot b}{\lambda}\\[5pt]
b_{\text{w}} &=&\dfrac{ \lambda_{\text{w}}}{\lambda} \cdot b &\quad \scriptsize \mid\; \lambda_{\text{w}} = 0,75 \cdot \lambda\\[5pt]
b_{\text{w}} &=&\dfrac{ 0,75 \cdot \lambda}{\lambda} \cdot b \\[5pt]
b_{\text{w}} &=& 0,75 \cdot b \\[5pt]
b_{\text{w}} &=& 0,75 \cdot 50 \text{ µm} \\[5pt]
b_{\text{w}} &=& 37,5 \text{ µm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/71f2e28ec514901e5ce546ddac890e4b79f7c666e46dc8ba1950782ddc481abd_light.svg) Die erforderliche Spaltbreite
Die erforderliche Spaltbreite  beträgt
beträgt  µm.
µm.
2
a)
Aus Aufgabe 1d) ist bereits bekannt, dass  ist. Einsetzen in die Formel für den Doppelspalt ergibt:
ist. Einsetzen in die Formel für den Doppelspalt ergibt:
![\(\begin{array}[t]{rll}
\sin \alpha_{\text{k}}&=& \dfrac{k \cdot \lambda}{g} &\quad \scriptsize \mid\; \cdot \dfrac{g}{\lambda} \\[5pt]
\dfrac{\sin \alpha_{\text{k}} \cdot g}{\lambda} &=& k \\[5pt]
\dfrac{\sin 20,6^\circ \cdot 50 \cdot 10^{-6} \text{ m}}{532 \cdot 10^{-9} \text{ m}} &=& k \\[5pt]
33,1 &=& k \\[5pt]
k &=& 33,1
\end{array}\)](https://www.schullv.de/resources/formulas/0ab4ff0044a504f993ec569fa96663f03f4b28e24bda856347db5674b8885060_light.svg) Also ist das Maximum höchster Ordnung das 33. Maximum. Insgesammt kann es also maximal
Also ist das Maximum höchster Ordnung das 33. Maximum. Insgesammt kann es also maximal  Maxima geben.
Diese Rechnung berücksichtigt nicht, dass manche Maxima vom Doppelspalt ausfallen können, da an dieser Stelle die beiden Spalte als Einzelspalt betrachtet ein Minumum erzwingen könnten.
Da der Spaltmittelabstand doppelt so groß ist wie die Einzelspaltbreite
Maxima geben.
Diese Rechnung berücksichtigt nicht, dass manche Maxima vom Doppelspalt ausfallen können, da an dieser Stelle die beiden Spalte als Einzelspalt betrachtet ein Minumum erzwingen könnten.
Da der Spaltmittelabstand doppelt so groß ist wie die Einzelspaltbreite  fällt jedes zweite Maxima aus. Es bleiben alle Maxima ungerader Ordnung übrig. Somit gibt es auf einer Seite
fällt jedes zweite Maxima aus. Es bleiben alle Maxima ungerader Ordnung übrig. Somit gibt es auf einer Seite  Maxima. Insgesammt gibt es also
Maxima. Insgesammt gibt es also  Maxima.
Maxima.
b)
Aus den beiden Abbildungen ist erkennbar, dass der Einfallswinkel stets größer als der Ausfallswinkel ist. Somit verschieben sich die Maxima zur Mitte hin. Desweiteren werden nun zwischen dem Maximum 33. Ordnung und dem Rand weitere Maxima hinzukommen.
c)
1. Schritt: Überlegung
 3. Schritt: Berechnung von
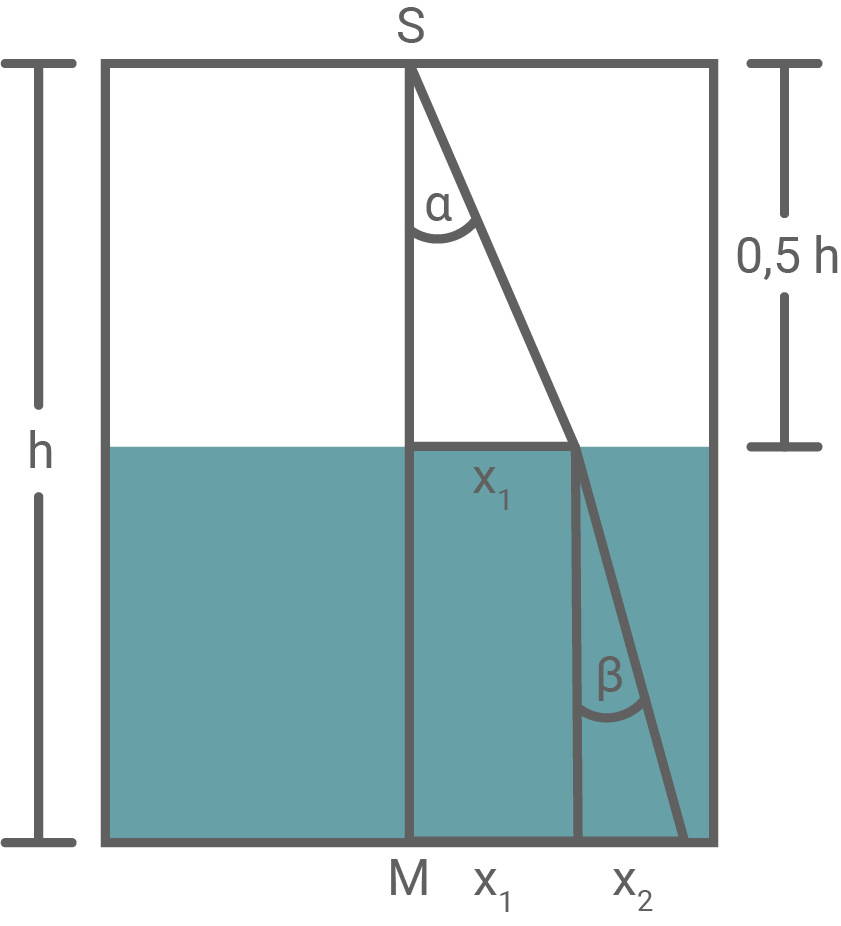
3. Schritt: Berechnung von  Für
Für  lässt sich folgende Dreiecksbeziehung ablesen:
4. Schritt: Bestimmung von
lässt sich folgende Dreiecksbeziehung ablesen:
4. Schritt: Bestimmung von  Aus dem in der Aufgabenstellung gegebenen Diagramm lässt sich ablesen, dass der Einfallswinkel
Aus dem in der Aufgabenstellung gegebenen Diagramm lässt sich ablesen, dass der Einfallswinkel  proportinal zu dem Ausfallswinkel
proportinal zu dem Ausfallswinkel  ist. Der Proportionalitätsfaktor beträgt
ist. Der Proportionalitätsfaktor beträgt  Somit ist
Somit ist 

 5. Schritt: Berechnung von
5. Schritt: Berechnung von  Für
Für  lässt sich folgende Dreiecksbeziehung ablesen:
6. Schritt: Berechnung der Verschiebung des Maximum 7. Ordung
Das neue Maximum 7. Ordnung ist
lässt sich folgende Dreiecksbeziehung ablesen:
6. Schritt: Berechnung der Verschiebung des Maximum 7. Ordung
Das neue Maximum 7. Ordnung ist 
 vom Mittelpunkt der Bodenplatte entfernt. Das alte Maximum 7. Ordnung ist
vom Mittelpunkt der Bodenplatte entfernt. Das alte Maximum 7. Ordnung ist 

 vom Mittelpunkt entfernt.
Das Maximum verschiebt sich also um
vom Mittelpunkt entfernt.
Das Maximum verschiebt sich also um 
 zur Mitte hin.
zur Mitte hin.
Die nebenstehenede Skizze beschreibt die Ausgangssituation. Das Licht wird am Doppelspalt  gebeugt. Der Winkel
gebeugt. Der Winkel  beschreibt den Winkel mit dem der Lichtstrahl gebeugt wird, der das Maximum 7. Ordnung erzeugt. Dieser Lichtstrahl trifft dann auf die Wasseroberfläche und wird um den Winke
beschreibt den Winkel mit dem der Lichtstrahl gebeugt wird, der das Maximum 7. Ordnung erzeugt. Dieser Lichtstrahl trifft dann auf die Wasseroberfläche und wird um den Winke  gebäugt. Schlussendlich trifft er auf den Boden ein.
2. Schritt: Berechnung des Winkels
gebäugt. Schlussendlich trifft er auf den Boden ein.
2. Schritt: Berechnung des Winkels 
![\(\begin{array}[t]{rll}
\sin \alpha_7 &=& \dfrac{7 \cdot \lambda}{g} \\[5pt]
\sin \alpha_7 &=& \dfrac{7 \cdot 532 \cdot 10^{-9} \text{ m}}{50 \cdot 10^{-6} \text{ m}} \\[5pt]
\sin \alpha_7 &=& 0,074 &\quad \scriptsize \mid\; \arcsin(...) \\[5pt]
\alpha_7 &=& 4,27 ^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/785f2cca1c2f46177d1c06bd5cc689ff25d82e1333226de7bf67ebeb19a4c43f_light.svg)

3
a)
Die positiv geladenen Ionen treten laut Aufgabenstellung senkrecht in das homogene Magnetfeld ein. Aufgrunddessen erfahren sie eine Lorenzkraft. Diese wirkt senkrecht auf die Bewegungsrichtung der Ionen und senkrecht auf das Magnetfeld. Somit wirkt diese als Zentripetalkraft und die Ionen bewegen sich im Kreis.
b)
Die Richtung der Ionen kann mit der Rechten-Hand-Regel bestimmt werden. Dabei repräsentiert der Daumen die Bewegungsrichtung eines positiven Ladungsträger, der Zeigefinger repräsentiert die Feldlinien des homogenen Magnetfelds und der Mittelfinger repräsentiert die Wirkungsrichtung der Lorenzkraft.
Wird der Mittelfinger zum Kreismittelpunkt und der Zeigefinger in die Zeichenebene gezeigt, so zeigt der Daumen gegen den Uhrzeigersinn. Die Ionen auf Bahn A bewegen sich also gegen den Uhrzeigersinn.
c)
Die Lorenzkraft ist gegeben durch folgende Formel:  Wie in Teilaufgabe a) aufgeführt, wirkt die Lorenzkraft als Zentripetalkraft. Somit ergibt sich folgender Zusammenhang:
Wie in Teilaufgabe a) aufgeführt, wirkt die Lorenzkraft als Zentripetalkraft. Somit ergibt sich folgender Zusammenhang:
![\(\begin{array}[t]{rll}
F_{\text{L}} &=& F_{\text{Z}} \\[5pt]
B \cdot q \cdot v &=& \dfrac{m \cdot v^2}{r} &\quad \scriptsize \mid\; \cdot \dfrac{r}{B \cdot q \cdot v} \\[5pt]
r &=& \dfrac{m}{B \cdot q} \cdot v \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/65fd0ba3dd255e71eee46a4d42981d6815332961a5a94bc715f0c13b67a9ca68_light.svg) Da der Faktor
Da der Faktor  jeweils für ein Ion konstant ist, sind
jeweils für ein Ion konstant ist, sind 
d)
1. Schritt: Vorüberlegung
Der allgmeine Bahnradius lässt sich mit der Formel aus c) berechnen.
2. Schritt: Formel für die Geschwindigkeit des Ions aufstellen
Die Geschwindigkeit des Ions lässt sich am besten über den Energieerhaltungssatz berechnen. Es gilt:
![\(\begin{array}[t]{rll}
E_{\text{kin}}&=& E_{\text{el}} \\[5pt]
\dfrac{1}{2} \cdot m \cdot v^2 &=& q \cdot U &\quad \scriptsize \mid\; \cdot \dfrac{2}{m} \\[5pt]
v^2 &=& \dfrac{2 \cdot q \cdot U}{m} &\quad \scriptsize \mid\; \sqrt{(...)} \\[5pt]
v &=& \sqrt{ \dfrac{2 \cdot q \cdot U}{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/787a14461356b62593e369e31820e3736ff9e06067bb2aa2bf7a5d4d85e739b1_light.svg) 3. Schritt: Formel für den Bahnradius aufstellen
Formel aus Teilaufgabe c):
3. Schritt: Formel für den Bahnradius aufstellen
Formel aus Teilaufgabe c):
![\(\begin{array}[t]{rll}
r &=& \dfrac{m}{B \cdot q} \cdot v \\[5pt]
r &=& \dfrac{m}{B \cdot q} \cdot \sqrt{ \dfrac{2 \cdot q \cdot U}{m}} \\[5pt]
r &=& \sqrt{ \dfrac{m^2 \cdot 2 \cdot q \cdot U}{B^2 \cdot q^2 \cdot m}} \\[5pt]
r &=& \sqrt{ \dfrac{2 \cdot m\cdot U}{B^2 \cdot q}} \\[5pt]
r &=& \sqrt{ \dfrac{2 \cdot U}{B^2}} \cdot \sqrt{ \dfrac{ m}{ q}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3fd67613eaada85599923f015a9dcbbc6e93a8bf6561fd1239b4d9a61d25e3f1_light.svg) Folglich ist
Folglich ist  4. Schritt: Berechnen aller Massen-Ladungsverhältnisse
4. Schritt: Berechnen aller Massen-Ladungsverhältnisse
5. Schritt: Berechnung des Bahnradius
Aus der Skizze in der Aufgabenstellung lässt sich folgender Sachverhalt ablessen:  Folglich gehört zu der Bahn A ein Massen-Ladungsverhältnis von
Folglich gehört zu der Bahn A ein Massen-Ladungsverhältnis von  Einsetzen in die Formel ergibt:
Folglich hat die Bahn A einen Radius von
Einsetzen in die Formel ergibt:
Folglich hat die Bahn A einen Radius von 
| Masse | Ladungsbetrag | Massen-Ladungs- verhältnis | |
|---|---|---|---|
| 1 |
1 |
1 |
|
| 2 |
1 |
2 |
|
| 4 |
1 |
4 |
|
| 4 |
2 |
2 |
e)
- Bahn A gehört wie in der voherigen Teilaufgabe berechnet zu Ionen mit einem Massen-Ladungsverhältnis von 2. Diese sind die
-Ionen und die
-Ionen.
- Bahn B hat den größten Radius und gehört deshalb zu Ionen mit einem Massen-Ladungsverhältnis von 4. Diese sind die
-Ionen.
- Bahn C hat den kleinsten Radius und gehört deshalb zu Ionen mit einem Massen-Ladungsverhältnis von 1. Diese sind die
-Ionen.