Aufgabe 2 – Licht

Monochromatisches Licht trifft senkrecht auf ein Gitter mit 250 Strichen pro cm. Parallel zur Gitterebene befindet sich im Abstand von $100\,\text{cm}$ ein $10\,\text{cm}$ breiter Schirm, auf dem ein Interferenzmuster zu sehen ist. Das Maximum nullter Ordnung befindet sich in der Mitte des Schirms.

Erkläre die Entstehung der Maxima und leite anhand geeigneter Skizzen eine Beziehung zwischen der Wellenlänge und dem Abstand zwischen den beiden Maxima k-ter Ordnung auf dem Schirm her.

Ein Hersteller gibt die Wellenlängen und Farben des Lichtes zweier von ihm produzierter LEDs wie folgt an: $\lambda_{\text {blau }}=465\,\text{nm}$ und $\lambda_{\text {grün }}=520\,\text{nm}.$ Das obige Gitter wird mit dem Licht der blauen LED beleuchtet und der Abstand gemessen, den die beiden Maxima k-ter Ordnung voneinander haben (siehe Tab.1).

$\color{#fff}{k}$	Abstand in $\color{#fff}{\text{cm}}$
1	2,3
2	4,7
3	7,0
4	9,2

Tabelle 1

Überprüfe die Herstellerangabe für die blaue LED unter Berücksichtigung aller Messwerte.

Bestimme die Anzahl der Maxima, die bei Verwendung der grünen LED auf dem Schirm zu sehen sind.

In einem weiteren Experiment mit obigem Aufbau verwendet man nun eine rote LED und die blaue LED aus Teilaufgabe b). Dabei stellt man fest, dass das Maximum 3. Ordnung des roten Lichts an der gleichen Position erscheint wie das Maximum 4. Ordnung des blauen Lichts.

Berechne die Wellenlänge des Lichtes der roten LED.

(10 VP)

In verschiedenen neuen Experimenten soll der Einfluss verschiedener Gitter und Lichtquellen auf die entstehenden Spektren untersucht werden. Hierzu stehen zunächst Gitter mit verschiedenen Spaltmittenabständen $g$ zur Verfügung (siehe Tab. 2).

Gitterbezeichnung	Spaltmittenabstand $\color{#fff}{g}$ in $\color{#fff}{\mu \text m}$
A	10
B	1
C	0,5

Tabelle 2

Es wird mit weißem Licht experimentiert, welches den gesamten sichtbaren Spektralbereich umfasst. Das komplette sichtbare Spektrum 1. Ordnung soll beobachtet werden.

Gib für jedes Gitter an, ob man mit ihm ein vollständiges Spektrum erzeugen kann, und begründe deine Angabe.

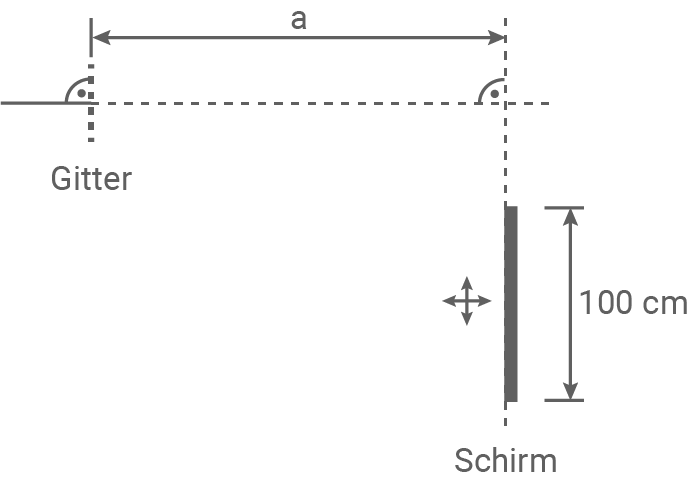
Zur Beobachtung des vollständigen Spektrums 1. Ordnung steht ein $100\,\text{cm}$ breiter Schirm zur Verfügung, welcher senkrecht und parallel zum Gitter verschiebbar ist (siehe Abb. 1). Eines der beiden Spektren 1. Ordnung soll unter Verwendung von Gitter B auf dem Schirm eine Breite von $100\,\text{cm}$ haben.

Abbildung 1

Bestimme den Abstand $a$ von Gitterebene und Schirmebene.

Bei einem weiteren Experiment wurde mit monochromatischem Licht und einem Gitter, dessen Öffnungen einen Mittenabstand von $125 \,\mu\text m$ haben, das in Abbildung 2 dargestellte Beugungsbild aufgenommen.

Abbildung 2

Erkläre, dass an bestimmten Stellen Maxima der Intensität ausfallen.

Bestimme anhand von Abbildung 2 die Breite der einzelnen Gitteröffnungen.

Das Emissionsspektrum des atomaren Wasserstoffs enthält unter anderem die Wellenlängen $\lambda_1=656\,\text{nm},$ $\lambda_2=486\,\text{nm}$ und $\lambda_3=434\,\text{nm}.$ Verwendet man bei einem Beugungsexperiment mit diesem Licht ein Gitter mit genügend großem Spaltmittenabstand $g,$ so kann man auch das Spektrum 2. und 3. Ordnung beobachten.

Zeige allgemein, dass auf jeden Fall eine Überlappung der Spektren 2. und 3. Ordnung auftritt.

(11 VP)

1999 gelang es einer Forschungsgruppe, Interferenz bei $C _{60}$ -Molekülen nachzuweisen. In einem Vakuum wurde ein Strahl aus $C _{60}$ -Molekülen erzeugt, die jeweils eine Masse von $1,20 \cdot 10^{-24}\,\text{kg}$ und eine mittlere Geschwindigkeit von $117 \,\text{m s} ^{-1}$ hatten. In diesen Strahl wurde senkrecht ein Beugungsobjekt eingebracht, das als Gitter aufgefasst werden kann. Mit einem Detektor wurden die auftreffenden Moleküle hinter dem Gitter registriert (siehe Abb. 3). Abbildung 4 zeigt die Anzahl der detektierten $C _{60}$ -Moleküle pro $100\,\text s$ in Abhängigkeit vom Abstand zum nullten Maximum.

Abbildung 3

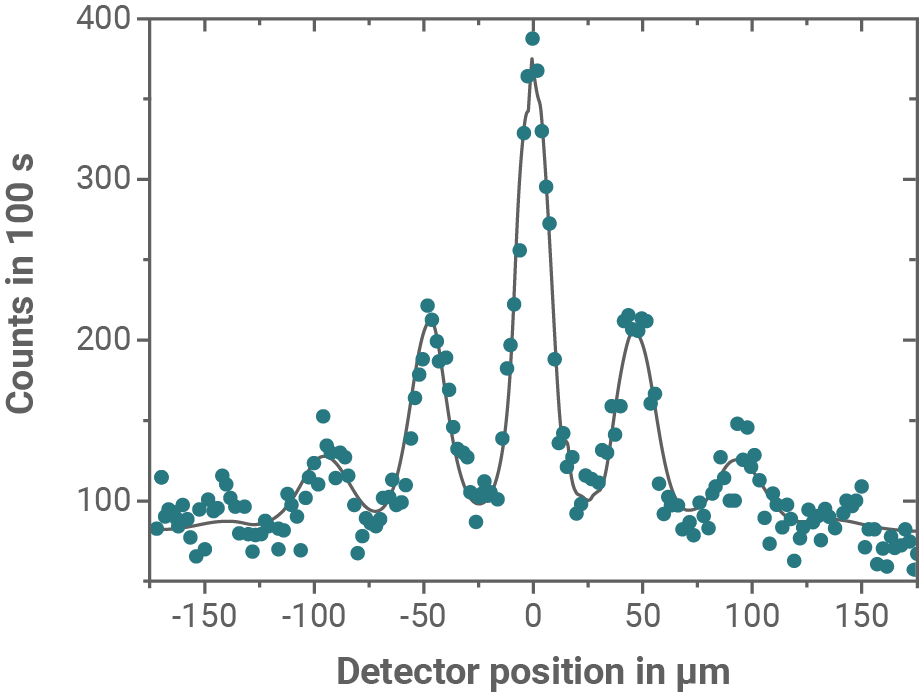
Abbildung 4

Erläutere anhand der Versuchsergebnisse, dass $C _{60}$ - Moleküle als Quantenobjekte aufgefasst werden müssen.

Berechne die mittlere de Broglie-Wellenlänge der $C_{60}$ -Moleküle.

Bestimme anhand von Abbildung 4 den Spaltmittenabstand des verwendeten Gitters.

Erkläre eine Veränderung des Interferenzbildes in Abbildung 4, falls man $C _{60}$ -Moleküle mit höherer mittlerer Geschwindigkeit verwendet.

Nimm an, dass bei einem leicht abgeänderten Experiment die Streuung der Molekülgeschwindigkeiten um den Mittelwert $117\,\text{ms} ^{-1}$ erheblich größer wäre, alle anderen Versuchsbedingungen aber gleich sind. Es ist zu erwarten, dass man ein im Vergleich zu Abbildung 4 verändertes Interferenzbild erhält.

Gib eine mögliche Veränderung an und begründe deine Antwort.

(9 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wenn die Lichtwellen auf den Doppelspalt treffen, werden sie gebeugt an den Spalten. Die Elementarwellen, die von den Spalten ausgehen interferieren miteinander auf dem Schirm.

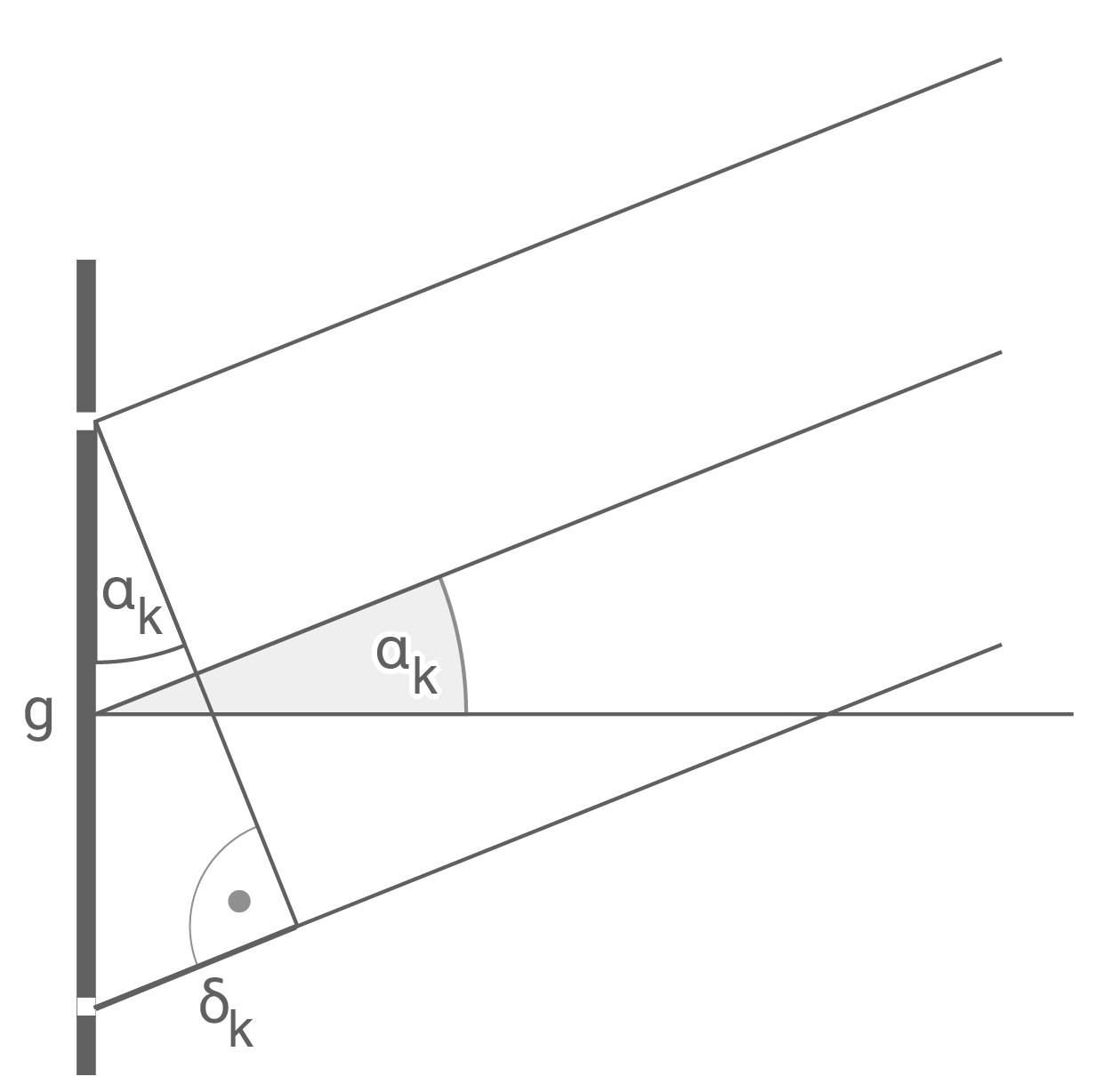Es gilt: $\sin(\alpha_k)=\dfrac{\delta_k}{g}$

Für $\alpha_k = k \cdot \lambda$ entstehen Intensitätsmaxima und für $\alpha_k = \dfrac{2k-1}{2}$ entstehen Intensitätsminima für $k=1;2;3;...$

Für Winkel mit $\sin(\alpha_k)=\dfrac{k \cdot \lambda}{g}$ entstehen Maxima, die Minima liegen dazwischen.

Die Abstände $d_k$ der Maxima vom Maximum 0. Ordnung lassen sich mit $\tan(\alpha_k)=\dfrac{d_k}{a}$ berechnen. $a$ entspricht dem Abstand des Schirms zum Doppelspalt.

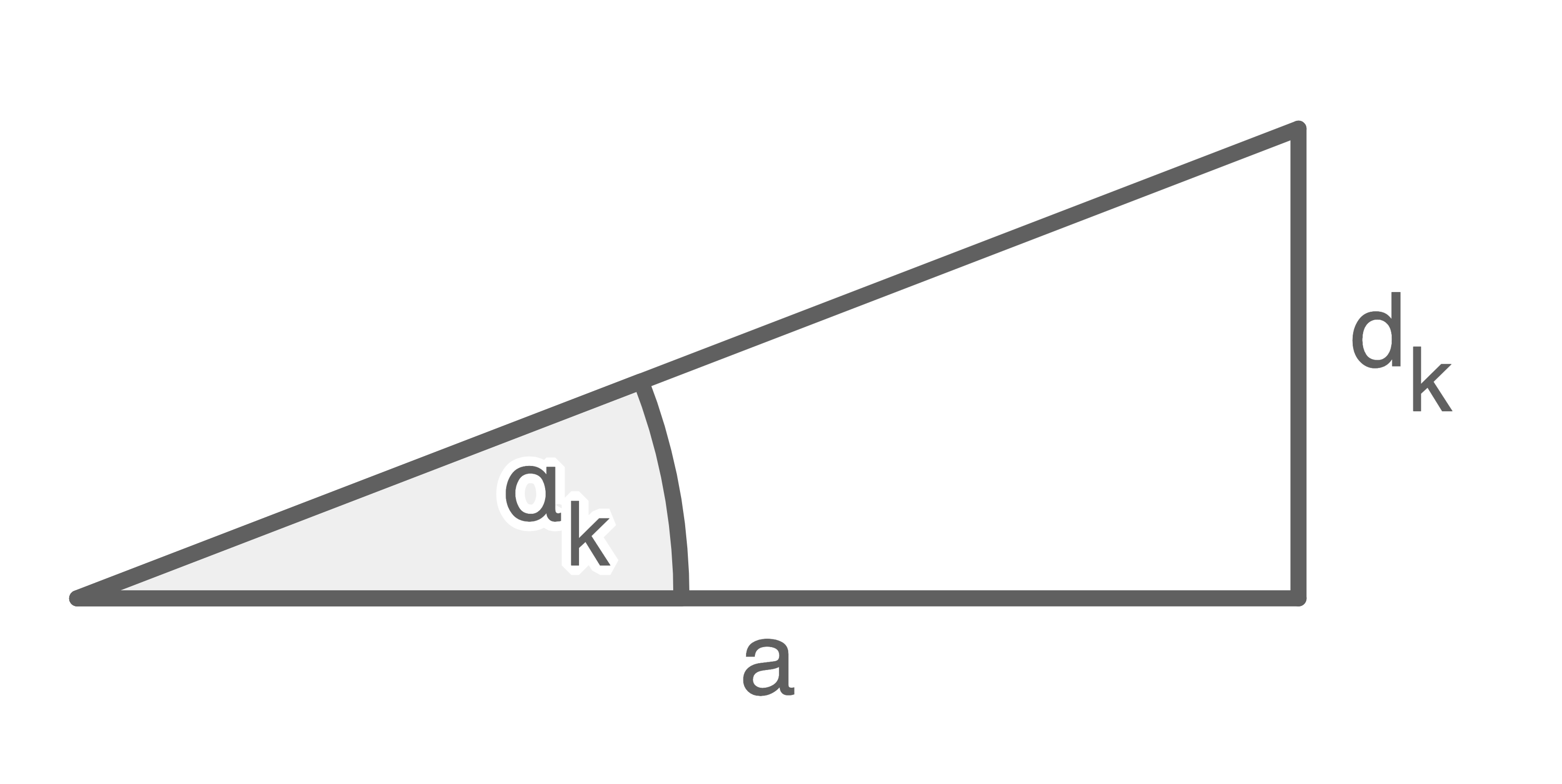Für kleine Winkel $\alpha_k$ gilt:

$\begin{array}[t]{rll} \sin (\alpha_k)&=& \tan (\alpha_k) \\[5pt] \dfrac{k \cdot \lambda}{g}&=& \dfrac{d_k}{a} &\quad \scriptsize \mid\;\cdot g \\[5pt] k \cdot \lambda&=& \dfrac{d_k}{a}\cdot g &\quad \scriptsize \mid\;\cdot\dfrac{1}{k} \\[5pt] \lambda&=& \dfrac{d_k\cdot g}{a\cdot k} &\quad \scriptsize \mid\;\Delta d_K=2 \cdot d_K \\[5pt] \lambda&=& \dfrac{\dfrac{\Delta d_k}{2}\cdot g}{a\cdot k} &\quad \scriptsize \\[5pt] \lambda &=&\dfrac{\Delta d_k\cdot g}{2\cdot a\cdot k} \end{array}$

Der Abstand der Gitteröffnungen $g$ beträgt:

$\begin{array}[t]{rll} g&=& \dfrac{1 \;\text{cm}}{250} &\quad \scriptsize \\[5pt] &=& 4 \cdot 10^{-5} \;\text{m} \end{array}$

Für den Schirmabstand $a$ gilt:

$\begin{array}[t]{rll} a&=& 100 \;\text{cm} &\quad \scriptsize \\[5pt] &=& 1 \;\text{m} &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte in die hergeleiteten Formel für $\lambda = \dfrac{g \cdot d_{k}}{a \cdot k}$ ergibt :

$\begin{array}[t]{rll} \lambda &=& \dfrac{d_{k}\cdot g}{a\cdot k}&\quad \scriptsize \\[5pt] &=& \dfrac{d_{k}\cdot 4 \cdot 10^{-5} \;\text{m}}{1 \;\text{m} \cdot k}&\quad \scriptsize \\[5pt] &=& 4 \cdot 10^{-5} \cdot \dfrac{d_{k}}{k}&\quad \scriptsize \\[5pt] \end{array}$

$\color{#fff}{k}$	$\color{#fff}{d_k}$ in $\color{#fff}{\text{cm}}$	$\color{#fff}{\lambda}$ in $\color{#fff}{\text{nm}}$
1	1,15	460
2	2,35	470
3	3,5	467
4	4,6	460

Für die Ordnung $k$ gilt:

$\begin{array}[t]{rll} \lambda &=& \dfrac{d_{k}\cdot g}{a\cdot k}&\quad \scriptsize \mid\; \cdot k \\[5pt] \lambda \cdot k&=& \dfrac{d_{k}\cdot g}{a} &\quad \scriptsize \mid\;\cdot \dfrac{1}{\lambda}\\[5pt] k&=&\dfrac{d_{k}\cdot g}{a\cdot \lambda} \end{array}$

Für den größtmögliche Abstand eines Maximums zur Schirmmitte $d_k$ gilt:

$\begin{array}[t]{rll} d_k&=& 5 \;\text{cm}&\quad \scriptsize \\[5pt] &=& 5 \cdot 10^{-2} \;\text{m} \end{array}$

Für den Abstand der Gitteröffnungen $g$ gilt:

$\begin{array}[t]{rll} g&=& 4 \cdot 10^{-5} \;\text{m} \end{array}$

Für den Schirmabstand $a$ gilt:

$\begin{array}[t]{rll} a&=& 1 \;\text{m} &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte in den Zusammenhang für $k$ liefert:

$\begin{array}[t]{rll} k&=&\dfrac{d_{k}\cdot g}{a\cdot \lambda_{\text{grün}}} &\quad \scriptsize \\[5pt] &=& \dfrac{4 \cdot 10^{-5} \;\text{m} \cdot 5 \cdot 10^{-2} \;\text{m}}{1 \;\text{m} \cdot 5,2 \cdot 10^{-7} \;\text{m}} &\quad \scriptsize \\[5pt] &=& 3,85 \end{array}$

Folglich sollten für diese Wellenlänge im Experiment $3+3+1=7$ Maxima auf dem Schirm zu sehen sein.

Umstellen der hergleiteten Formel nach $d_k$ lierfert:

$\begin{array}[t]{rll} k&=&\dfrac{d_{k}\cdot g}{a\cdot \lambda} &\quad \scriptsize \mid\;\cdot \dfrac{\lambda \cdot a}{g} \\[5pt] \dfrac{\lambda \cdot a \cdot k}{g}&=& d_k &\quad \scriptsize \\[5pt] d_k&=& \dfrac{\lambda \cdot a \cdot k}{g} \end{array}$

Die Bedingung für das Zusammenfallen der beiden genannten Maxima lautet:

$\begin{array}[t]{rll} d&=& \dfrac{3 \cdot \lambda_{\text {rot }} \cdot a}{g}&\quad \scriptsize \\[5pt] &=& \dfrac{4 \cdot \lambda_{\text {blau }} \cdot a}{g} \end{array}$

Umstellen des Zusammenhangs nach $\lambda_{\text {rot }}$ liefert:

$\begin{array}[t]{rll} \dfrac{3 \cdot \lambda_{\text {rot }} \cdot a}{g}&=& \dfrac{4 \cdot \lambda_{\text {blau }} \cdot a}{g}&\quad \scriptsize \mid\; \cdot \dfrac{g}{a} \\[5pt] 3 \cdot \lambda_{\text {rot }} &=& \dfrac{4 \cdot \lambda_{\text {blau }} \cdot a\cdot g}{g\cdot a}&\quad \scriptsize \mid\; \cdot \dfrac{1}{3} \\[5pt] \lambda_{\text {rot }} &=& \dfrac{4}{3} \cdot \lambda_{\text {blau }} \end{array}$

Einsetzen des Wertes für $\lambda_{\text {blau }}$ liefert:

$\begin{array}[t]{rll} \lambda_{\text {rot }} &=& \dfrac{4}{3} \cdot \lambda_{\text {blau }} &\quad \scriptsize \\[5pt] &=& \dfrac{4}{3} \cdot 465 \;\text{nm} &\quad \scriptsize \\[5pt] &=& 620 \;\text{nm} \end{array}$

Maxima 1.Ordnung der Gitterbeugung treten auf für die Winkel $\alpha_1:$

$\begin{array}[t]{rll} \sin (\alpha_k)&=& \dfrac{k \cdot \lambda}{g}&\quad \scriptsize \mid\; k=1 \\[5pt] \sin (\alpha_1)&=& \dfrac{1 \cdot \lambda}{g} \end{array}$

Die Beugungswinkel nehmen mit abnehmender Gitterkonstante zu. Das Spektrum erster Ordnung ist genau dann unvollständig, wenn für die größte Wellenlänge des sichtbaren Bereichs der Wert $\dfrac{\lambda_{\max }}{g}>1$ ist.

Bei dem Gitter C mit der kleinsten Gitterkonstanten gilt:

$\begin{array}[t]{rll} \dfrac{\lambda_{\max }}{g_C}&=&\dfrac{800 \;\text{nm}}{0,5 \;\mu \text{m}} &\quad \scriptsize \\[5pt] &=& 1,6 \end{array}$

Für Gitter B gilt:

$\begin{array}[t]{rll} \dfrac{\lambda_{\max }}{g_B}&=&\dfrac{800 \;\text{nm}}{1 \;\mu \text{m}} &\quad \scriptsize \\[5pt] &=& 0,8 \end{array}$

Also ist Gitter $C$ ungeeignet zur Erzeugung des vollständigen Spektrums 1. Ordnung. Gitter B, und damit auch Gitter A mit der größten Gitterkonstanten aller Gitter, sind prinzipiell zur Beobachtung geeignet.

Für die Beugungswinkel der Maxima 1. Ordnung gilt:

$\begin{array}[t]{rll} \sin (\alpha_1)&=& \dfrac{1 \cdot \lambda}{g_B} &\quad \scriptsize \mid\; \sin^{-1}\left(\;\right) \\[5pt] \alpha_1&=& \sin^{-1}\left(\dfrac{\lambda}{g_B}\right) \end{array}$

Für die Wellenlänge $400 \;\text{nm}$ beträgt der Grenzwinkel:

Rechenweg anzeigen

$\alpha_{1, \min }= 23,6^{\circ}$

Für die Wellenlänge $800 \;\text{nm}$ beträgt der Grenzwinkel:

Rechenweg anzeigen

$\alpha_{1, \max } = 53,1^{\circ}$

Für den Abstand der Ränder des Spektrums 1.Ordnung auf dem Schirm gilt:

Rechenweg anzeigen

$a=\dfrac{\Delta d}{\tan\left( \alpha_{1, \max }\right)- \tan \left(\alpha_{1, \min }\right)}$

Einsetzen der Werte liefert für die gewünsche Breite $\Delta d$ des Spektrums den gesuchten Schirmabstand $a:$

$\begin{array}[t]{rll} a&=& \dfrac{\Delta d}{\tan\left( \alpha_{1, \max }\right)- \tan \left(\alpha_{1, \min }\right)}&\quad \scriptsize \\[5pt] &=& \dfrac{1 \;\text{m}}{\tan \left(53,1^{\circ}\right)- \tan \left(23,6^{\circ}\right)}&\quad \scriptsize \\[5pt] &=& 1,12 \;\text{m} \end{array}$

Die Intensität der Lichtpunkte wird beeinflusst von der Beugung des Lichts an den einzelnen Öffnungen mit der Breite $b$ , die das jeweilige Gitter besitzt. In den Richtungen, bei denen ein Minimum der Einzelspaltbeugung vorliegt, entfällt ein sonst eigentlich zu erwartendes Maximum der Gitterbeugung.

In Abbildung 2 ist zu erkennen, dass jedes fünfte Maximum der Gitterbeugung nicht zu sehen ist. Die Richtungen zum Maximum fünfter Ordnung der Gitterbeugung und zum Minimum 1.Ordnung der Spaltbeugung stimmen überein. $b$ enspricht der Breite der Gitteröffnung. Es gilt:

$\begin{array}[t]{rll} \dfrac{5 \cdot \lambda}{g}&=& \dfrac{1 \cdot \lambda}{b}&\quad \scriptsize \mid\;\cdot b \\[5pt] \dfrac{5 \cdot \lambda}{g}\cdot b&=& \lambda &\quad \scriptsize \mid\;\cdot \dfrac{g}{5 \cdot \lambda} \\[5pt] b&=& \dfrac{g \cdot \lambda}{5 \cdot \lambda}&\quad \scriptsize \\[5pt] b&=& \dfrac{g}{5 } &\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte liefert für die Breite der Öffnung des vorliegenden Gitters:

$\begin{array}[t]{rll} b&=& \dfrac{g}{5 } &\quad \scriptsize \\[5pt] &=& \dfrac{125 \;\mu\text{m}}{5 } &\quad \scriptsize \\[5pt] &=& 25 \;\mu\text{m} \end{array}$

Eine Überlappung der Spektren 2. und 3. Ordnung des Wasserstoffspektrums liegt vor, wenn der Beugungswinkel für das Licht mit der Wellenlänge $\lambda_1$ in der 2 . Ordnung größer ist als der Beugungswinkel für Licht der Wellenlänge $\lambda_3$ in der 3 . Ordnung.

Für den den Beugungswinkel $\alpha_{2,1}$ der Wellenlänge $\lambda_1$ in der 2 . Ordnung gilt:

$\begin{array}[t]{rll} \sin \left(\alpha_{2,1}\right)&=& \dfrac{2 \cdot \lambda_1}{g}&\quad \scriptsize \\[5pt] &=& \dfrac{2 \cdot 656 \;\text{nm}}{g}&\quad \scriptsize \\[5pt] &=& \dfrac{1312 \;\text{nm}}{g} &\quad \scriptsize \\[5pt] \end{array}$

Für den den Beugungswinkel $\alpha_{3,3}$ der Wellenlänge $\lambda_3$ in der 3 . Ordnung gilt:

$\begin{array}[t]{rll} \sin \left(\alpha_{3,3}\right)&=& \dfrac{3 \cdot \lambda_1}{g}&\quad \scriptsize \\[5pt] &=& \dfrac{3 \cdot 434\;\text{nm}}{g}&\quad \scriptsize \\[5pt] &=& \dfrac{1302 \;\text{nm}}{g} &\quad \scriptsize \\[5pt] \end{array}$

Vergleichen der Ergebnisse für $\sin \alpha_{2,1}$ und $\sin \alpha_{3,3}$ liefert:

$\begin{array}[t]{rll} \dfrac{1312 \;\text{nm}}{g}&>& \dfrac{1302 \;\text{nm}}{g}&\quad \scriptsize \mid\; \cdot g \\[5pt] 1312 \;\text{nm}&>& 1302\;\text{nm} &\quad \scriptsize \\[5pt] \sin \left(\alpha_{2,1}\right)&>& \sin \left(\alpha_{3,3} \right) &\quad \scriptsize \\[5pt] \alpha_{2,1}&>& \alpha_{3,3} \end{array}$

Der Winkel $\alpha_{2,1}$ ist unabhängig von g immer größer als $\alpha_{3,3}$ , daher überlappen sich die Wasserstoffspektren in der 2. und 3.Ordnung.

Treffen die Moleküle mit der genannten Geschwindigkeit auf ein geeignetes Gitter, so sind Beugungserscheinungen mit deutlich ausgeprägten Maxima und Minima der Auftreffwahrscheinlichkeit an den Positionen, die der Detektor durchläuft (siehe Abbildung 4), zu beobachten. Aus diesem Grund lässt sich den Molekülen nach den Gesetzen der Quantenphysik eine Wahrscheinlichkeitswelle zuordnen, und sie können somit als Quantenobjekte aufgefasst werden.

Für die mittlere de Broglie-Wellenlänge der Moleküle gilt:

$\begin{array}[t]{rll} \lambda&=&\dfrac{h}{p} &\quad \scriptsize \\[5pt] &=& \dfrac{h}{m \cdot v} \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} \lambda&=&\dfrac{h}{m \cdot v} &\quad \scriptsize \\[5pt] &=& \dfrac{6,63 \cdot 10^{-34} \;\text{Js}}{1,20 \cdot 10^{-24} \;\text{kg} \cdot 117 \;\text{ms}^{-1}} &\quad \scriptsize \\[5pt] &=& 4,72 \cdot 10^{-12} \;\text{m} \end{array}$

Aus dem Interferenzbild in Abbildung 4 lässt sich ablesen, dass das Maximum 2. Ordnung von dem Maximum 0. Ordnung auf dem Schirm etwa $95 \; \mu \text{m}$ entfernt ist. Der Schirmabstand ist groß, die Kleinwinkelnäherung ist folglich erlaubt. Damit gilt:

$\begin{array}[t]{rll} \dfrac{2 \cdot \lambda}{g}&=&\dfrac{d_2}{a}&\quad \scriptsize \mid\; \cdot g\\[5pt] 2 \cdot \lambda&=& \dfrac{d_2}{a}\cdot g &\quad \scriptsize \mid\; \cdot \dfrac{a}{d_2}\\[5pt] \dfrac{2 \cdot \lambda\cdot a}{d_2}&=& g \end{array}$

Einsetzen der Werte liefert:

$\begin{array}[t]{rll} g&=&\dfrac{2 \cdot \lambda\cdot a}{d_2}&\quad \scriptsize \\[5pt] &=& \dfrac{2 \cdot 4,72 \cdot 10^{-12} \;\text{m} \cdot 1,25 \;\text{m}}{95 \; \mu \text{m}}&\quad \scriptsize \\[5pt] &=& \dfrac{2 \cdot 4,72 \cdot 10^{-12} \;\text{m} \cdot 1,25 \;\text{m}}{95 \cdot 10^{-6} \;\text{m}}&\quad \scriptsize \\[5pt] &=& 1,2 \cdot 10^{-7} \;\text{m} \end{array}$

Bei einer größeren mittleren Molekülgeschwindigkeit $v$ ist die Wellenlänge $\lambda=\dfrac{h}{p}=\dfrac{h}{m \cdot v}$ der Wahrscheinlichkeitswelle kleiner. Der Abstand der Maxima höherer Ordnung zum Maximum 0. Ordnung wird kleiner.

Die Berge und Täler des Beugungsbilds werden nicht mehr so stark ausgeprägt sein wie in Abbildung 4. Durch die größere Streuung der Geschwindigkeitswerte der Moleküle liegen die Maxima für die unterschiedlichen Geschwindigkeiten an verschiedenen Stellen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?