Aufgabe 3 – Felder
1.
Elektronen mit vernachlässigbarer Anfangsgeschwindigkeit werden im homogenen elektrischen Feld eines Plattenkondensators durch die Spannung 
beschleunigt (siehe Abb. 1). Anschließend gelangen die Elektronen durch die rechte Öffnung bei 
in ein homogenes magnetisches Feld mit der Flussdichte 
Die Anordnung befindet sich im Vakuum.
beschleunigt (siehe Abb. 1). Anschließend gelangen die Elektronen durch die rechte Öffnung bei in ein homogenes magnetisches Feld mit der Flussdichte Die Anordnung befindet sich im Vakuum.
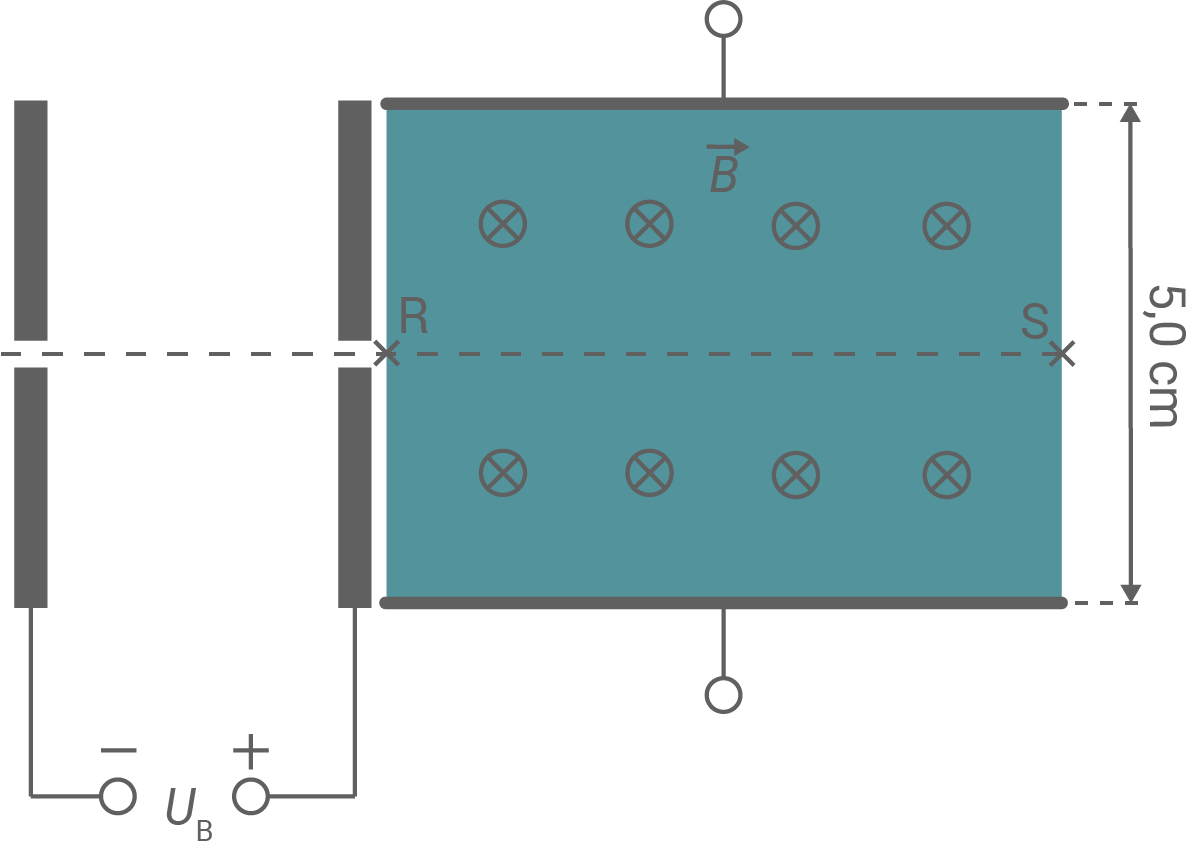
Abbildung 1
a)
Zeige, dass die Elektronen bei die Geschwindigkeit 
besitzen.
die Geschwindigkeit besitzen.
b)
Erkläre, warum die Elektronen beim Eintritt in das Magnetfeld eine Ablenkung erfahren und gib die Richtung der Ablenkung an.
Senkrecht zum magnetischen Feld soll nun mit Hilfe eines weiteren Kondensators mit horizontalen Platten ein elektrisches Feld mit der Feldstärke 
erzeugt werden, damit die Elektronen die Anordnung geradlinig von nach 
durchlaufen (siehe Abb. 1).
c)
Bestimme für diesen Fall den Betrag und die Richtung der elektrischen Feldstärke.
d)
Berechne die Spannung zwischen den horizontalen Platten.
e)
Erkläre das Verhalten der Elektronen direkt nach dem Passieren des Punktes 
, wenn die Beschleunigungsspannung 
verringert wird.
In einem weiteren Experiment werden Teilchen gleicher Ladung , wenn die Beschleunigungsspannung verringert wird.
aber unterschiedlicher Masse in der Apparatur aus Abbildung 1 durch eine Spannung beschleunigt.
f)
Zeige, dass für die Masse 
der Teilchen, welche die gesamte Apparatur geradlinig durchlaufen, folgende Beziehung gilt:
der Teilchen, welche die gesamte Apparatur geradlinig durchlaufen, folgende Beziehung gilt:
(10 VP)
2.
Eine luftgefüllte Zylinderspule besitzt 100 Windungen und hat einen ohmschen Widerstand von 
. Der Radius 
beträgt 
, die Länge 
der Spule ist so veränderbar, dass die Windungen gleichmäßig über die jeweilige Spulenlänge verteilt sind (siehe Abb. 2). An den Spulenenden wird eine Spannung von 
angelegt.
. Der Radius beträgt , die Länge der Spule ist so veränderbar, dass die Windungen gleichmäßig über die jeweilige Spulenlänge verteilt sind (siehe Abb. 2). An den Spulenenden wird eine Spannung von angelegt.
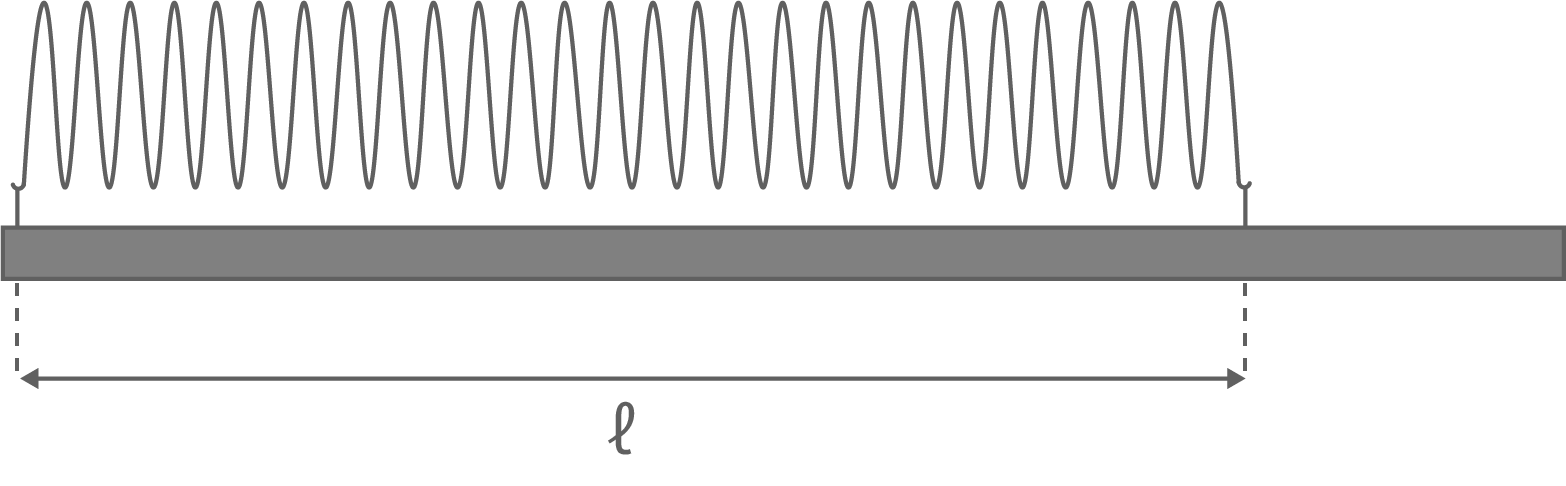
Abbildung 2
in der jeweiligen Spulenmitte von der Spulenlänge abhängt. Tabelle 1 enthält die Messwerte des Versuchs.
 in  |
 in  |
|---|---|
| 0,06 | 6,25 |
| 0,08 | 5,48 |
| 0,10 | 4,95 |
| 0,15 | 3,64 |
| 0,20 | 2,90 |
| 0,30 | 2,05 |
| 0,40 | 1,59 |
| 0,63 | 0,96 |
| 1,50 | 0,40 |
a)
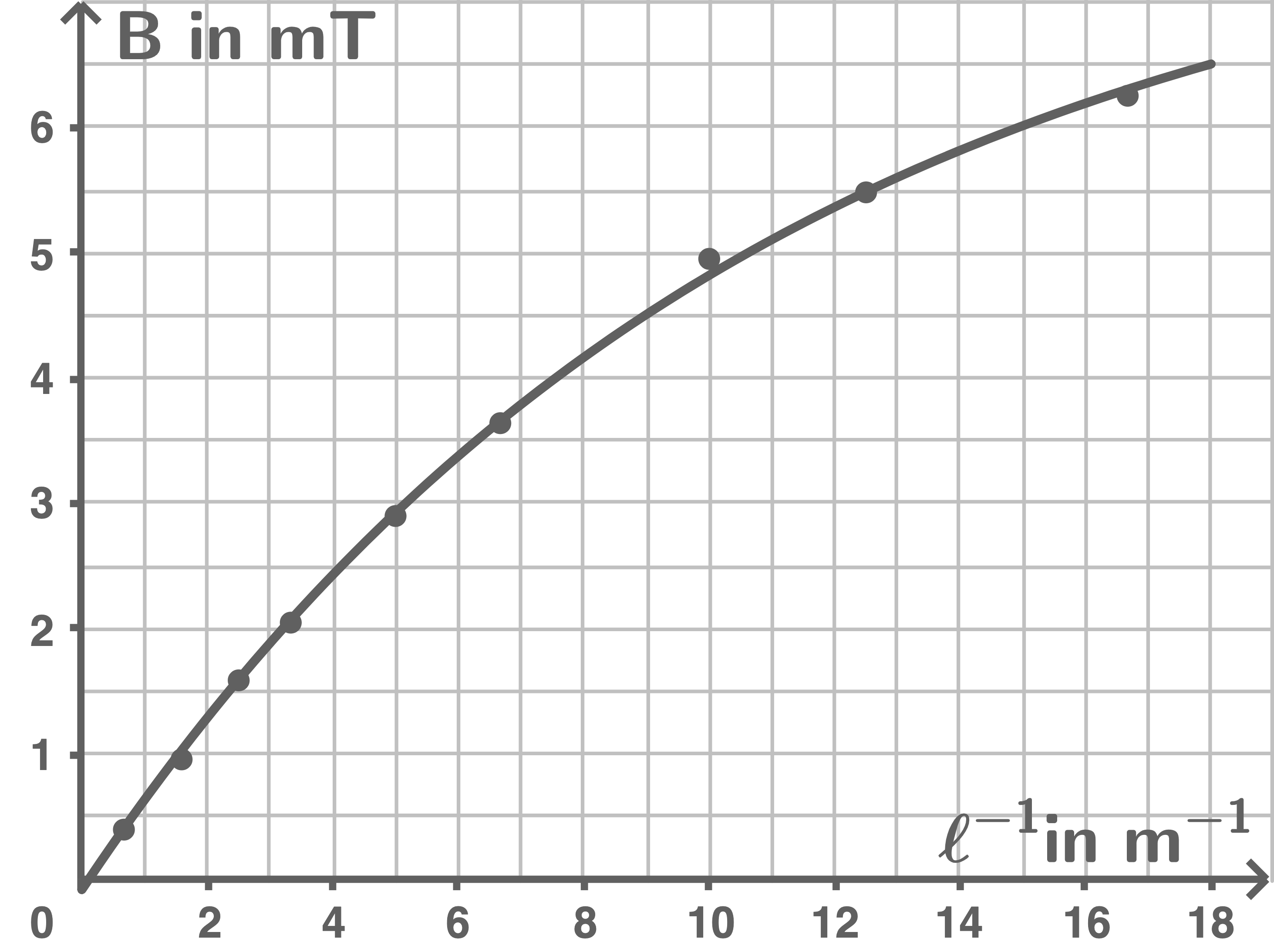
Zeichne ein Diagramm, das die Abhängigkeit der magnetischen Flussdichte vom Kehrwert der Spulenlänge zeigt.
b)
Bestimme die Länge der Spule, bei der die magnetische Flussdichte 
beträgt.
beträgt.
c)
Zeichne in das Diagramm aus Teilaufgabe a) den Verlauf der magnetischen Flussdichte ein, den man bei Verwendung der Formel für langgestreckte Spulen erwarten würde.
In der Versuchsanleitung wird darauf hingewiesen, dass bei diesem Versuch die Formel für die magnetische Flussdichte langgestreckter Spulen 
mit einem Faktor korrigiert werden muss. Es ergibt sich für den korrekten Wert der magnetischen Flussdichte in der Spulenmitte folgenden Zusammenhang:
d)
Bestimme bei der vorliegenden Spule die Mindestlänge, die einzustellen ist, damit um weniger als 
von in der Spulenmitte abweicht.
um weniger als von in der Spulenmitte abweicht.
(8 VP)
3.
Zwischen zwei quadratischen Metallplatten der Kantenlänge 
befinden sich an den Ecken kleine gleichartige Schaumstoffpolster (siehe Abb. 3). Die Anordnung kann in guter Näherung wie ein luftgefüliter Plattenkondensator behandelt werden.
befinden sich an den Ecken kleine gleichartige Schaumstoffpolster (siehe Abb. 3). Die Anordnung kann in guter Näherung wie ein luftgefüliter Plattenkondensator behandelt werden.
Abbildung 3
zentral auf die obere Platte auflegt. An die Anschlüsse 
und 
in Abbildung 3 wird ein elektronisches Kapazitätsmessgerät angeschlossen. Das Diagramm in Abbildung 4 zeigt den Zusammenhang zwischen der gemessenen Kapazität und der Masse des aufgelegten Massestücks.
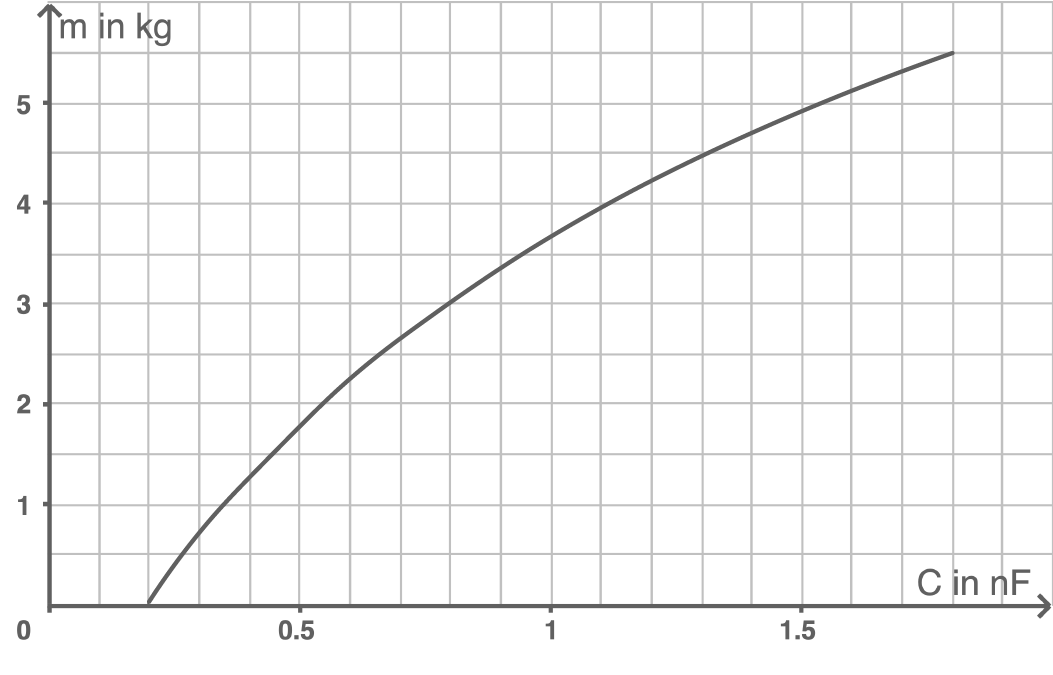
Abbildung 4
a)
Begründe, warum bei größerer gemessener Kapazität die aufgelegte Masse größer sein muss.
b)
Bestimme den Abstand der Platten im unbelasteten Zustand.
Nun wird zum Schutz der Apparatur beim Zusammendrücken der Abstand der beiden Platten auf ein Minimum von 
begrenzt.
c)
Ermittle die maximale Masse, die mit dieser Anordnung dann noch bestimmt werden kann.
Das verwendete Kapazitätsmessgerät liefert über den gesamten Messbereich eine Messgenauigkeit von 
.
d)
Beurteile, ob auch die Genauigkeit der Massenbestimmung über den gesamten Messbereich gleich ist.
Experimentell lässt sich die Kapazität des Kondensators dadurch bestimmen, dass man die Platten mit einer Spannung von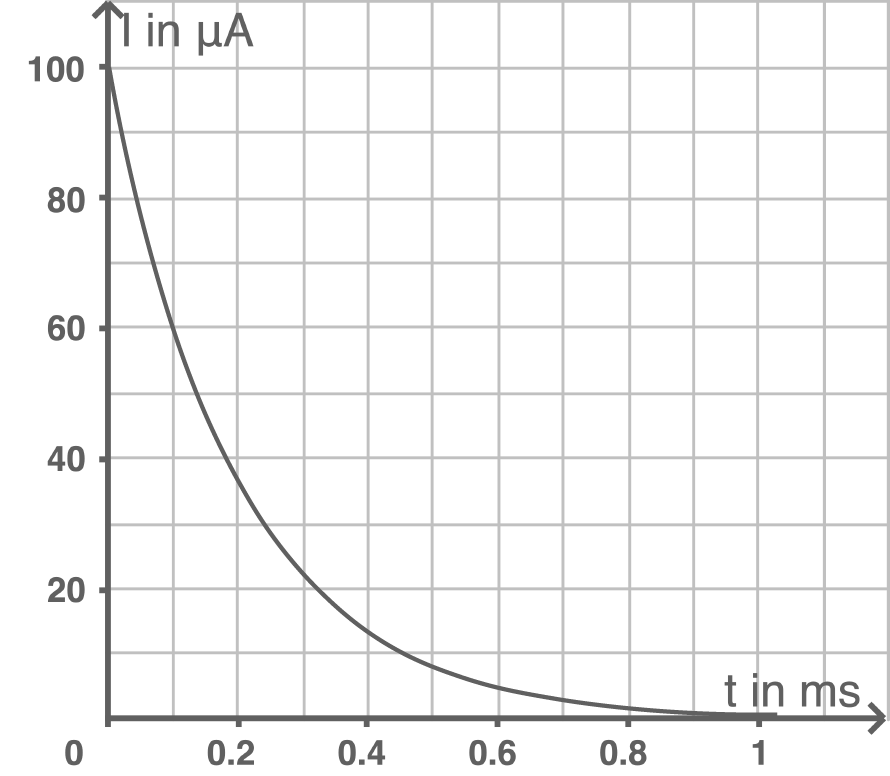 
auflädt und anschließend über einen ohmschen Widerstand entlädt. Abbildung 5 zeigt den Verlauf der Stromstärke ab Beginn des Entladevorgangs bei einem solchen Experiment.
Abbildung 5
e)
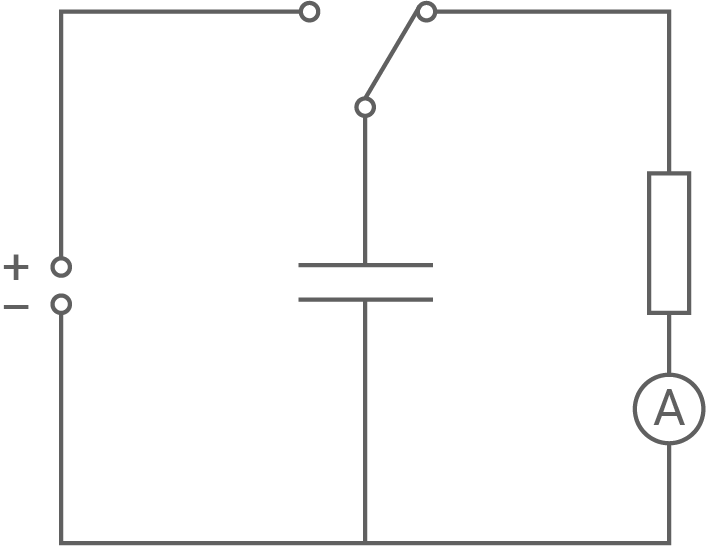
Skizziere eine Schaltung, mit der diese Messung durchgeführt werden kann.
f)
Bestimme unter Verwendung des Zeit - Stromstärke - Diagramms näherungsweise die Kapazität des Kondensators.
(12 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die Elektronen werden mit Hilfe der Spannung 
beschleunigt. Aus dem Energieerhaltungssatz folgt:
beschleunigt. Aus dem Energieerhaltungssatz folgt:
![\(\begin{array}[t]{rll}
E_\text{kin}&=& E_\text{el} \\[5pt]
\dfrac{1}{2} \cdot m \cdot v^2 &=& e \cdot U_\text{B} &\quad \scriptsize \mid\; \cdot \dfrac{2}{m} \\[5pt]
v^2 &=& \dfrac{2 \cdot e \cdot U_\text{B}}{m} &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
v &=& \sqrt{ \dfrac{2 \cdot e \cdot U_\text{B}}{m}} \\[5pt]
v &=& \sqrt{2 \cdot \dfrac{1,60 \cdot 10^{-19} \mathrm{C}}{9,11 \cdot 10^{-31} \mathrm{~kg}} \cdot 800 \mathrm{~V}} \\[5pt]
v &=& 1,68 \cdot 10^{7} \mathrm{~ms}^{-1} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/66bdec7daa1c171713850462abcf5b6d22ac74fa792742e6df5982b0d77d068d_light.svg)
b)
Anwendung der Linken-Hand-Regel
Daumen: Gibt die Richtung negativer Ladungsträger an und zeigt somit nach rechts.
Zeigefinger: Gibt die Richtung der magnetischen Feldlinien an und zeigt somit in die Zeichenebene hinein.
Mittelfinger: Gibt die Richtung der Lorentzkraft an und zeigt folglich nach unten. Somit erfahren die Elektronen eine Lorentzkraft, die senkrecht zur urspünglichen Flugrichtung nach unten wirkt.
Daumen: Gibt die Richtung negativer Ladungsträger an und zeigt somit nach rechts.
Zeigefinger: Gibt die Richtung der magnetischen Feldlinien an und zeigt somit in die Zeichenebene hinein.
Mittelfinger: Gibt die Richtung der Lorentzkraft an und zeigt folglich nach unten. Somit erfahren die Elektronen eine Lorentzkraft, die senkrecht zur urspünglichen Flugrichtung nach unten wirkt.
c)
Da sich die Anordnung im Vakuum befindet, wird die Gravitationskraft nicht berücksichtigt. Folglich fliegen die Elektronen senkrecht durch den Versuchsaufbau, falls die elektrische und die magnetische Feldkraft im Kräftegleichgewicht ist.
![\(\begin{array}[t]{rll}
\overrightarrow{F_\text{el}} &=& \overrightarrow{F_\text{Lor}} \\[5pt]
e \cdot E &=& e \cdot v \cdot B \quad \scriptsize \mid\; : e\\[5pt]
E &=& v \cdot B \\[5pt]
E &=& 1,68 \cdot 10^{7} \mathrm{~ms}^{-1} \cdot 1,8 \cdot 10^{-3} \mathrm{~T} \\[5pt]
E &=& 3,0 \cdot 10^{4} \mathrm{~Vm}^{-1}
\end{array}\)](https://www.schullv.de/resources/formulas/69f81ce4b8ba255c627ec358059b7eeaa2d485fe32c0eece8ced2da2c6f39bc0_light.svg)
Die magnetische Kraft 
zeigt nach unten zeigt und die elektrische Kraft 
nach oben. Deshalb ist die obere Platte positiv geladen und somit zeigen die Feldlinien zur unteren Platte.
Die magnetische Kraft zeigt nach unten zeigt und die elektrische Kraft nach oben. Deshalb ist die obere Platte positiv geladen und somit zeigen die Feldlinien zur unteren Platte.
d)
Es gilt:
![\(\begin{array}[t]{rll}
U &=& E \cdot d \\[5pt]
U &=& 3,0 \cdot 10^{4} \mathrm{~Vm}^{-1} \cdot 5,0 \mathrm{~cm}\\[5pt]
U &=& 1,5 \cdot 10^{3} \mathrm{~V} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5a58ff162bbafb84f17d70b1076286cea6ba3b4b248edfe529ecaf9411d92d31_light.svg)
e)
Die bei ankommenden Elektronen besitzen eine kleinere Energie und damit eine kleinere Geschwindigkeit. Die unveränderte elektrische Kraft ist nun betragsmäßig größer im Vergleich zur Lorentzkraft. Die Elektronen weichen beim Feldeintritt nun in den Bereich oberhalb der Geraden 
ab.
ankommenden Elektronen besitzen eine kleinere Energie und damit eine kleinere Geschwindigkeit. Die unveränderte elektrische Kraft ist nun betragsmäßig größer im Vergleich zur Lorentzkraft. Die Elektronen weichen beim Feldeintritt nun in den Bereich oberhalb der Geraden ab.
f)
Nach Teilaufgabe c) gilt:
![\(\begin{array}[t]{rll}
v \cdot B &=& E &\quad \scriptsize \mid\; :B \\[5pt]
v &=& \dfrac{E}{B}
\end{array}\)](https://www.schullv.de/resources/formulas/6a6155e13b115cfb25079b1a59efb1d637199ae71191afb34a45f50178d2f301_light.svg)
Nach Teilaufgabe a) gilt:
![\(\begin{array}[t]{rll}
v^2 &=& \dfrac{2 \cdot q \cdot U_\text{B}}{m} \\[5pt]
\left( \dfrac{E}{B} \right)^2 &=& \dfrac{2 \cdot q \cdot U_\text{B}}{m} &\quad \scriptsize \mid\; \cdot \dfrac{m \cdot B^2}{E^2} \\[5pt]
m &=& \dfrac{2 \cdot q \cdot U_\text{B} \cdot B^2}{E^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/11ed6775661747c5e9368020f3e75c74af7907ac12f90ee6ebbafbb44316fd86_light.svg)
Nach Teilaufgabe a) gilt:
2
a)
 in |
in |
 in  |
|---|---|---|
| 0,06 | 6,25 | 16,67 |
| 0,08 | 5,48 | 12,50 |
| 0,10 | 4,95 | 10,00 |
| 0,15 | 3,64 | 6,67 |
| 0,20 | 2,90 | 5,0 |
| 0,30 | 2,05 | 3,33 |
| 0,40 | 1,59 | 2,50 |
| 0,63 | 0,96 | 1,59 |
| 1,50 | 0,40 | 0,67 |
b)
Aus dem Diagramm wird abgelesen:
Zur magnetischen Flussdichte 6,00 
auf der horizontalen Achse ein Wert von ca. 
Daraus ergibt sich eine Spulenlänge von 
.
auf der horizontalen Achse ein Wert von ca.
Daraus ergibt sich eine Spulenlänge von .
c)
Für die Steigung im Diagramm gilt:
![\(\begin{array}[t]{rll}
\dfrac{\Delta B}{\Delta \ell^{-1}}&=& \Delta B \cdot \Delta \ell \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/14d8f08f9a2bc11c6e1972e3b3815f061dfbaea1e57cb234c939aa2cd2baa440_light.svg)
Die magnetische Flussdichte einer langgestreckten Spule lässt sich berechnen mit:
Folglich beträgt die Steigung der Ursprungsgerade 
Die magnetische Flussdichte einer langgestreckten Spule lässt sich berechnen mit:
Folglich beträgt die Steigung der Ursprungsgerade 
![\(\begin{array}[t]{rll}
B_{\text {lang }} &=& \mu_{0} \cdot \mu_{r} \cdot \dfrac{n}{\ell} \cdot I &\quad \scriptsize \mid\; I=\dfrac{U}{R} \\[5pt]
B_{\text {lang }} &=& \mu_{0} \cdot \mu_{r} \cdot \dfrac{n}{\ell} \cdot \dfrac{U}{R} &\quad \scriptsize \mid\; \cdot \ell \\[5pt]
B_{\text {lang }} \cdot \ell &=& \mu_{0} \cdot \mu_{r} \cdot n \cdot \dfrac{U}{R} \\[5pt]
B_{\text {lang }} \cdot \ell &=& 1,26 \cdot 10^{-6} \dfrac{\mathrm{Vs}}{\mathrm{Am}} \cdot 1 \cdot 100 \cdot \dfrac{10 \mathrm{~V}}{2 \Omega} \\[5pt]
B_{\text {lang }} \cdot \ell &=& 6,3 \cdot 10^{-4} \mathrm{~Tm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/28d4685d096e6a1c2312a12b3565fad145eac90ebeccee14a2a3c603e7775a12_light.svg)
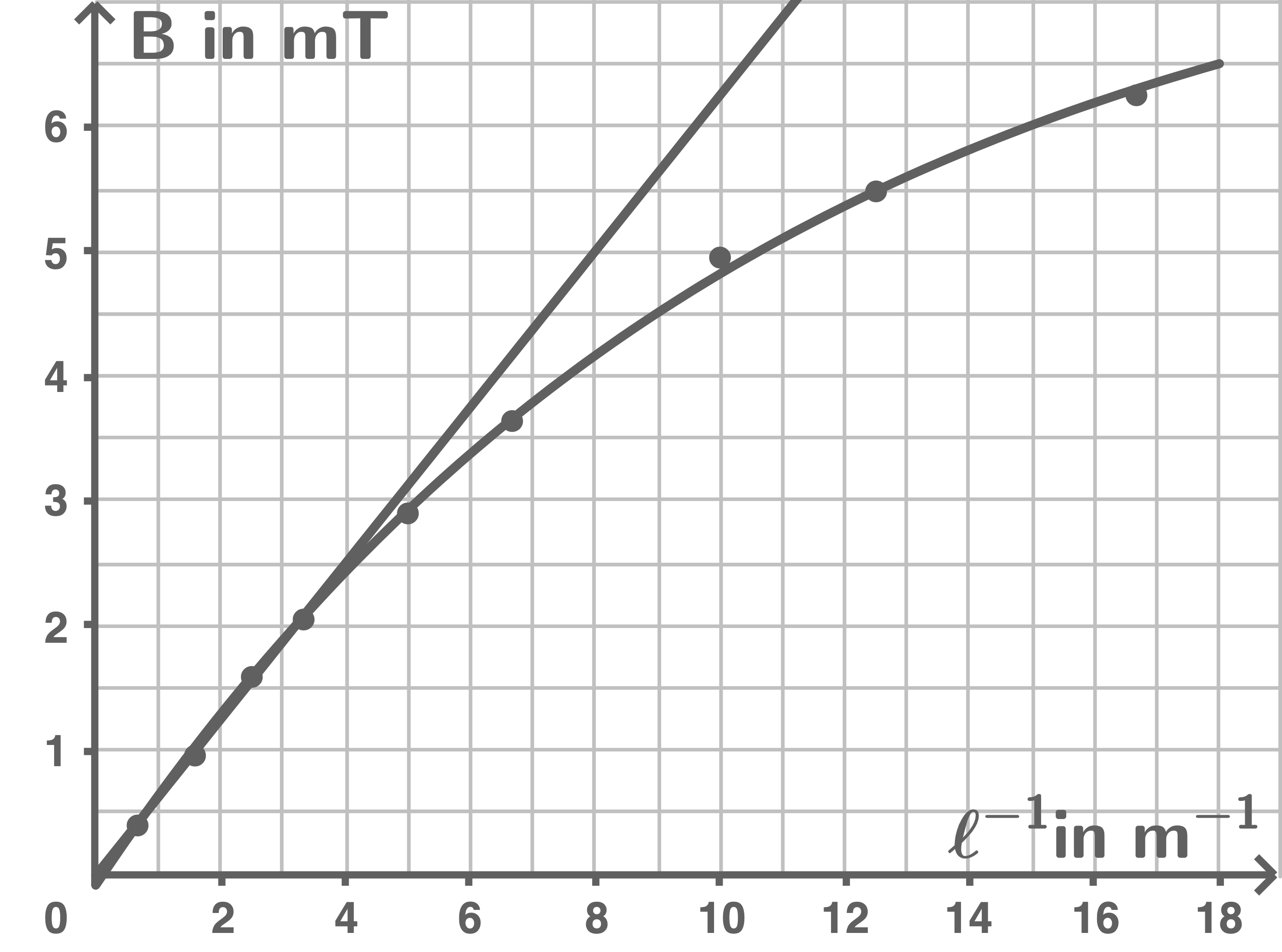
d)
Aus dem Diagramm aus Teilaufgabe c) ergibt sich, dass 
ist. Abweichungen von oder weniger erhält man ab der Spulenlänge, für die gilt:
ist. Abweichungen von oder weniger erhält man ab der Spulenlänge, für die gilt:
![\(\begin{array}[t]{rll}
\dfrac{B_{\text {lang }}-B}{B} &\lt& 0,05 \\[5pt]
\dfrac{B_{\text {lang }}}{B} - \dfrac{B}{B} &\lt& 0,05 \\[5pt]
\dfrac{B_{\text {lang }}}{B} - 1 &\lt& 0,05 &\quad \scriptsize \mid\; + 1 \\[5pt]
\dfrac{B_{\text {lang }}}{B} &\lt& 1,05 \\[5pt]
\sqrt{1+\dfrac{4 \cdot r^{2}}{\ell^{2}}} &\lt& 1,05 &\quad \scriptsize \mid\; (\;)^2 \\[5pt]
1+\dfrac{4 \cdot r^{2}}{\ell^{2}} &\lt& 1,05^2 &\quad \scriptsize \mid\; -1 \\[5pt]
\dfrac{4 \cdot r^{2}}{\ell^{2}} &\lt& 1,05^2 - 1 &\quad \scriptsize \mid\; \cdot \dfrac{\ell^{2}}{1,05^2 - 1} \\[5pt]
\dfrac{4 \cdot r^{2}}{1,05^2 - 1} &\lt& \ell^{2} &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\dfrac{2 \cdot r}{\sqrt{1,05^2 - 1}} &\lt& \ell \\[5pt]
\ell &\gt& \dfrac{2 \cdot r}{\sqrt{1,05^2 - 1}} \\[5pt]
\ell &\gt& \dfrac{2 \cdot 4,0 \text{ cm}}{\sqrt{1,05^2 - 1}} \\[5pt]
\ell &\gt& 25,0 \text{ cm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b659b023ffddf06be9346b752938dcf76610eb3e9027830388ef4f4ae2d754d2_light.svg)
3
a)
Da die Kapazität umgekehrt proportional zum Plattenabstand ist, muss bei größerer gemessener Kapazität der Plattenabstand kleiner werden. Dies ist dann der Fall, wenn eine größere Masse auflegt wird.
b)
Aus dem Schaubild wird als kleinste Kapazität ca. 
abgelesen. Diese gehört zum unbelasteten Kondensator.
Der Plattenabstand ergibt sich aus:
![\(\begin{array}[t]{rll}
C &=& \varepsilon_{0} \cdot \varepsilon_{r} \cdot \dfrac{A}{d} \quad \quad \scriptsize \mid\; \cdot d \; \mid \; :C\\[5pt]
d &=& \varepsilon_{0} \cdot \varepsilon_{r} \cdot \dfrac{A}{C} \\[5pt]
d &=& 8,85 \cdot 10^{-12} \dfrac{\text{As}}{\text{Vm}} \cdot 1 \cdot \dfrac{(0,5 \mathrm{~m})^{2}}{0,2 \text{nF}}\\[5pt]
d &=& 11,1 \mathrm{~mm}
\end{array}\)](https://www.schullv.de/resources/formulas/9de3a7e428f8bf4bbd5405414ea20ff3708cbc1adcd9fe8efc5e0a3458b4a73f_light.svg)
abgelesen. Diese gehört zum unbelasteten Kondensator.
Der Plattenabstand ergibt sich aus:
c)
Beim Abstand 
hat der Kondensator eine Kapazität von
![\(\begin{array}[t]{rll}
C &=& \varepsilon_{0} \cdot \varepsilon_{r} \cdot \frac{A}{d} \\[5pt]
C &=& 8,85 \cdot 10^{-12} \dfrac{\mathrm{Vs}}{\mathrm{Am}} \cdot 1 \cdot \dfrac{(0,5 \mathrm{~m})^{2}}{1,5 \;\mathrm{mm}}\\[5pt]
C &=& 1,48 \; \mathrm{nF}
\end{array}\)](https://www.schullv.de/resources/formulas/cc2c588364dc826491efac4e38b444dca5103f921d9e21cb208eda36d384f5b0_light.svg)
Dazu gehört eine aufgelegte Masse von ca. 
.
hat der Kondensator eine Kapazität von
Dazu gehört eine aufgelegte Masse von ca. .
d)
Dem Schaubild wird entnommen, dass bei einem zuvor unbelasteten Kondensator für eine Kapazitätsänderung von 
ca. 
aufgelegt werden. Bei einem zuvor z.B. mit 
belasteten Kondensator genügt für eine Kapazitätssteigerung von schon das Auflegen einer Zusatzmasse von ca. 
.
Das zeigt, dass die Genauigkeit der Massenbestimmung nicht über den gesamten Bereich gleich ist.
ca. aufgelegt werden. Bei einem zuvor z.B. mit belasteten Kondensator genügt für eine Kapazitätssteigerung von schon das Auflegen einer Zusatzmasse von ca. .
Das zeigt, dass die Genauigkeit der Massenbestimmung nicht über den gesamten Bereich gleich ist.
e)
f)
Ein Maß für die abgeflossene Ladung ist der Flächeninhalt unter der Stromkurve. Sie lässt sich z.B. durch das Legen einer Sekante im Schaubild ermitteln, sodass ein flächengleiches Dreieck entsteht. Aus einer Höhe von 
und der Grundseite von 
ergibt sich als Ladung:
![\(\begin{array}[t]{rll}
Q &=& \dfrac{1}{2} \cdot 100 \; \mu \mathrm{A} \cdot 0,4 \mathrm{~ms} \\[5pt]
Q &=& 20 \; \mathrm{nC}
\end{array}\)](https://www.schullv.de/resources/formulas/aca1a244e0f4ed49ad871804da881d34a35d67398033cc84714fd8d99d0e9f6c_light.svg)
Damit ergibt sich eine Kapazität
![\(\begin{array}[t]{rll}
C &=& \dfrac{Q}{U} \\[5pt]
C &=& \dfrac{20 \mathrm{nC}}{50 \mathrm{~V}} \\[5pt]
C &=& 400 \; \mathrm{pF}
\end{array}\)](https://www.schullv.de/resources/formulas/f3b981adb22d44a31d8c4609be3e3c9451fc319be17b3d289a30bc4fc09edac5_light.svg)
und der Grundseite von ergibt sich als Ladung:
Damit ergibt sich eine Kapazität