Aufgabe 3 – Elektromagnetismus
1.
Ein ungeladener Kondensator und ein dazu in Reihe geschalteter Widerstand von  werden zum Zeitpunkt
werden zum Zeitpunkt  an ein Netzgerät mit einer konstanten Gleichspannung angeschlossen. Mithilfe eines Messwerterfassungssystems, welches parallel zum Widerstand geschaltet ist, werden die Werte für die Stromstärke beim Ladevorgang im Sekundenabstand aufgezeichnet (siehe Tabelle 1).
an ein Netzgerät mit einer konstanten Gleichspannung angeschlossen. Mithilfe eines Messwerterfassungssystems, welches parallel zum Widerstand geschaltet ist, werden die Werte für die Stromstärke beim Ladevorgang im Sekundenabstand aufgezeichnet (siehe Tabelle 1).
 beschreiben.
beschreiben.
| 0 | 500 |
| 1,00 | 322 |
| 2,00 | 205 |
| 3,00 | 130 |
| 4,00 | 78,5 |
| 5,00 | 51,0 |
| 6,00 | 32,0 |
| 7,00 | 22,0 |
| 8,00 | 13,0 |
| 9,00 | 10,0 |
| 10,00 | 5,50 |
Tabelle 1
a)
Zeichne für dieses Experiment ein Schaltbild.
b)
Zeichne das zugehörige Zeit-Stromstärke-Diagramm.
c)
Zeige, dass die Spannung am Netzgerät  beträgt.
beträgt.
Der Verlauf der Stromstärke lässt sich mithilfe der Funktion
d)
Bestimme einen Wert für die Kapazität des Kondensators.
e)
Ermittle die Ladungsmenge, die in den ersten zwei Sekunden auf den Kondensator fließt, und vergleiche diesen Wert mit der Ladungsmenge des vollständig geladenen Kondensators.
2.
Die Abbildung 1 zeigt das Schnittbild einer kugelförmigen und einer quaderförmigen Metallelektrode sowie im Bereich dazwischen elektrische Feldlinien. Zusätzlich sind Linien gleichen Potenzials, sogenannte Äquipotenziallinien, gestrichelt eingezeichnet. Die Potenzialdifferenz zwischen den dargestellten benachbarten Äquipotenziallinien ist konstant. Diese Potenzialdifferenz besteht auch zwischen den Elektroden und der nächstliegenden Äquipotenziallinie. Die quaderförmige Elektrode hat das Potenzial  und die kugelförmige Elektrode das Potenzial
und die kugelförmige Elektrode das Potenzial 
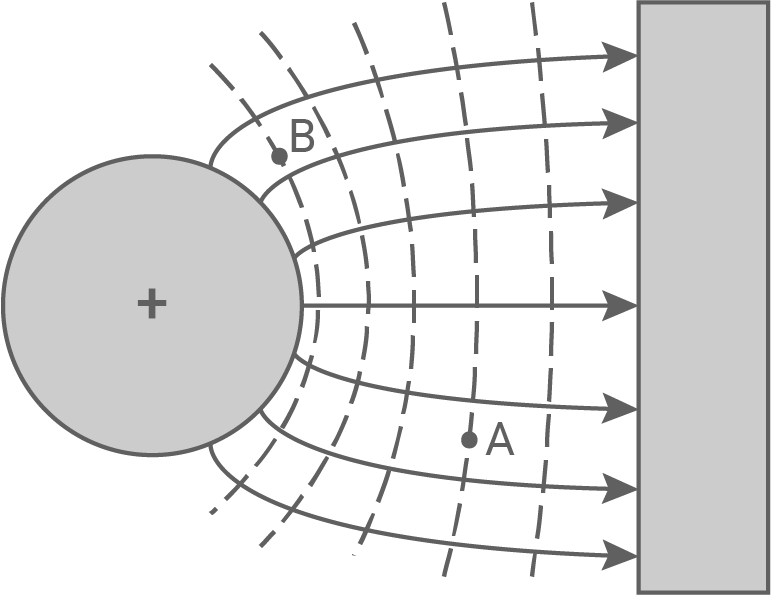
Abbildung 1
a)
Bestimme das Potenzial im Punkt 
b)
Bestimme die Energie, die notwendig wäre, um ein Proton von  nach
nach  zu verschieben.
zu verschieben.
Nun wird die quaderförmige Elektrode entfernt. In das Feld der kugelförmigen Elektrode wird eine kleine Kugel mit der Ladung In einer Versuchsreihe wird die elektrische Kraft
| 5,00 | 24,5 |
| 10,00 | 6,05 |
| 20,0 | 1,52 |
| 30,0 | 0,68 |
| 50,0 | 0,24 |
c)
Untersuche, welcher der folgenden Zusammenhänge durch die Messung bestätigt wird. Dabei ist  eine Konstante.
(1)
eine Konstante.
(1)  (2)
(2)  (3)
(3)  (4)
(4)  (5)
(5) 
Für die Konstante
d)
Berechne unter Verwendung aller Messwerte die Ladung  der kugelförmigen Elektrode.
der kugelförmigen Elektrode.
(7 VP)
3.
In dem in der Abbildung dargestellten Schaltkreis befinden sich zwei baugleiche Lämpchen  und
und  ein ohmscher Widerstand R und eine Spule
ein ohmscher Widerstand R und eine Spule 
Für die folgenden Überlegungen soll angenommen werden, dass der Widerstand der Lämpchen jeweils konstant beträgt.
beträgt.
Der Widerstand und die Spule SP haben jeweils den ohmschen Widerstand
und die Spule SP haben jeweils den ohmschen Widerstand  Die Induktivität der Spule beträgt
Die Induktivität der Spule beträgt 
Zum Zeitpunkt wird der Schalter
wird der Schalter  geschlossen. Man beobachtet, dass
geschlossen. Man beobachtet, dass  gegenüber
gegenüber  zeitverzögert zu leuchten beginnt.
zeitverzögert zu leuchten beginnt.
Für die folgenden Überlegungen soll angenommen werden, dass der Widerstand der Lämpchen jeweils konstant
Der Widerstand
Zum Zeitpunkt
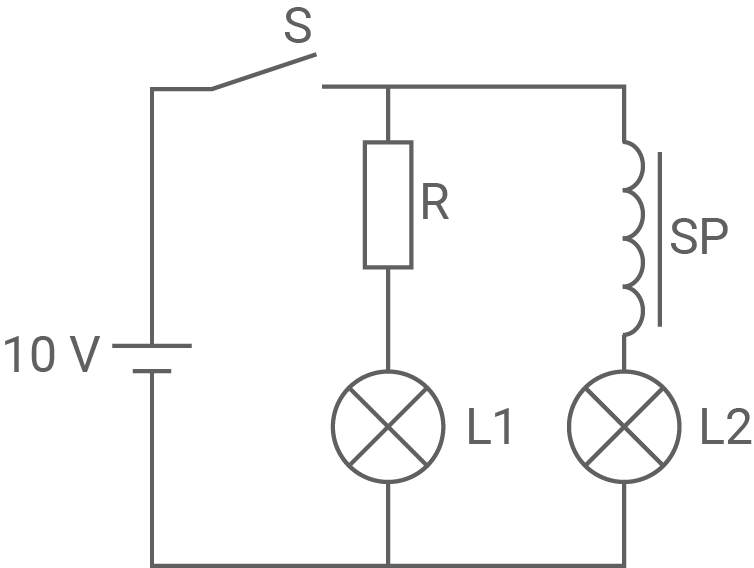
Abbildung 2
a)
Erkläre diese Beobachtung.
Nun wird der Schalter wieder geöffnet.
b)
Beschreibe, wie sich die Lämpchen nun verhalten, und begründe deine Antwort.
c)
Begründe, warum der Betrag der in der Spule induzierten Spannung unmittelbar nach dem Öffnen des Schalters  beträgt.
beträgt.
Abbildung 3 zeigt den Verlauf der elektrischen Stromstärke in der Spule für diesen Ein- und Ausschaltvorgang.
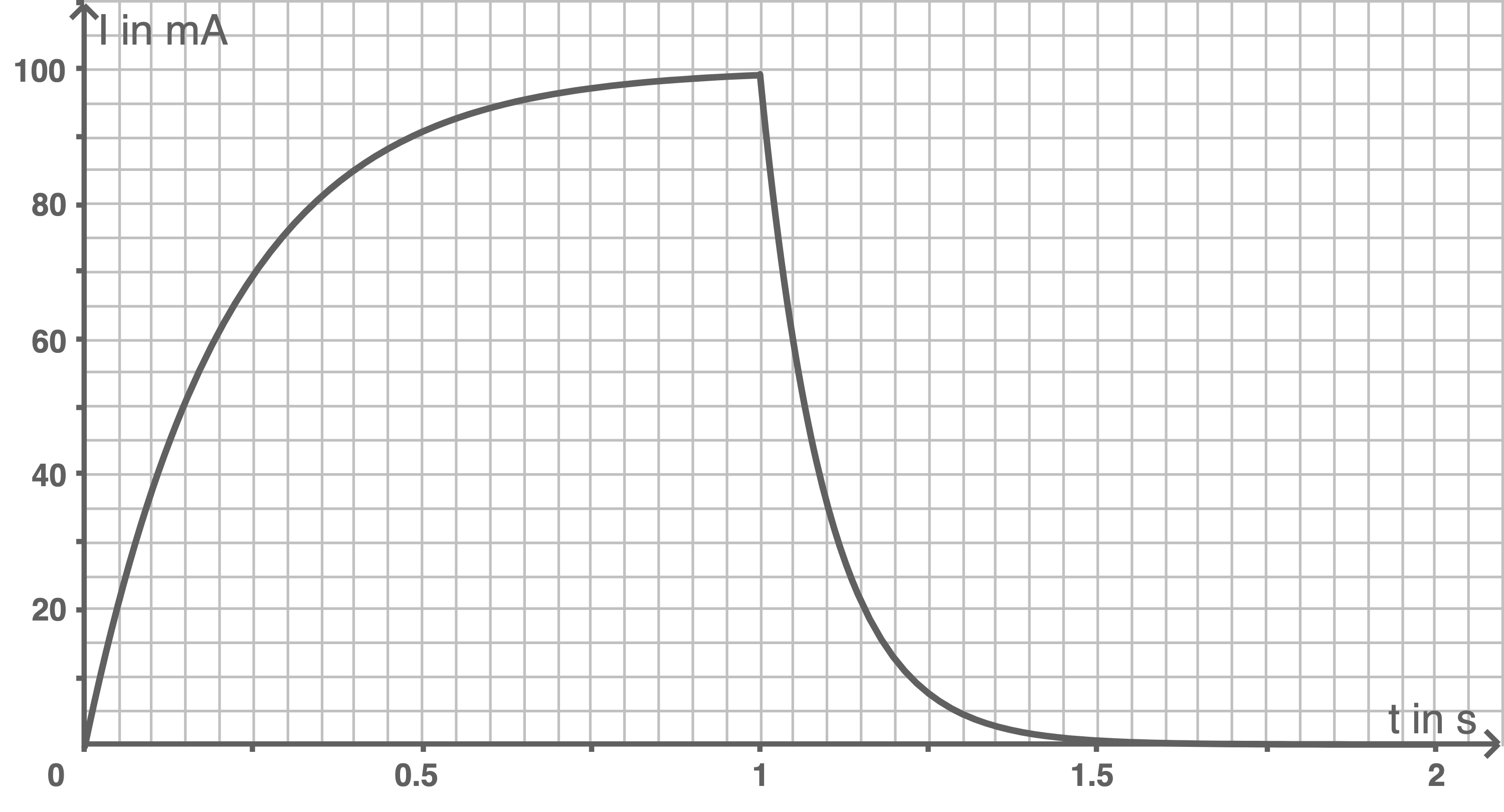
Abbildung 3
d)
Bestimme näherungsweise die Werte der in der Spule induzierten Spannung für die Zeitpunkte  und
und 
e)
Skizziere den Verlauf der in der Spule induzierten Spannung in das Koordinatensystem von Abbildung 4 unter Verwendung der in den Teilaufgaben c und d bestimmten Werte.
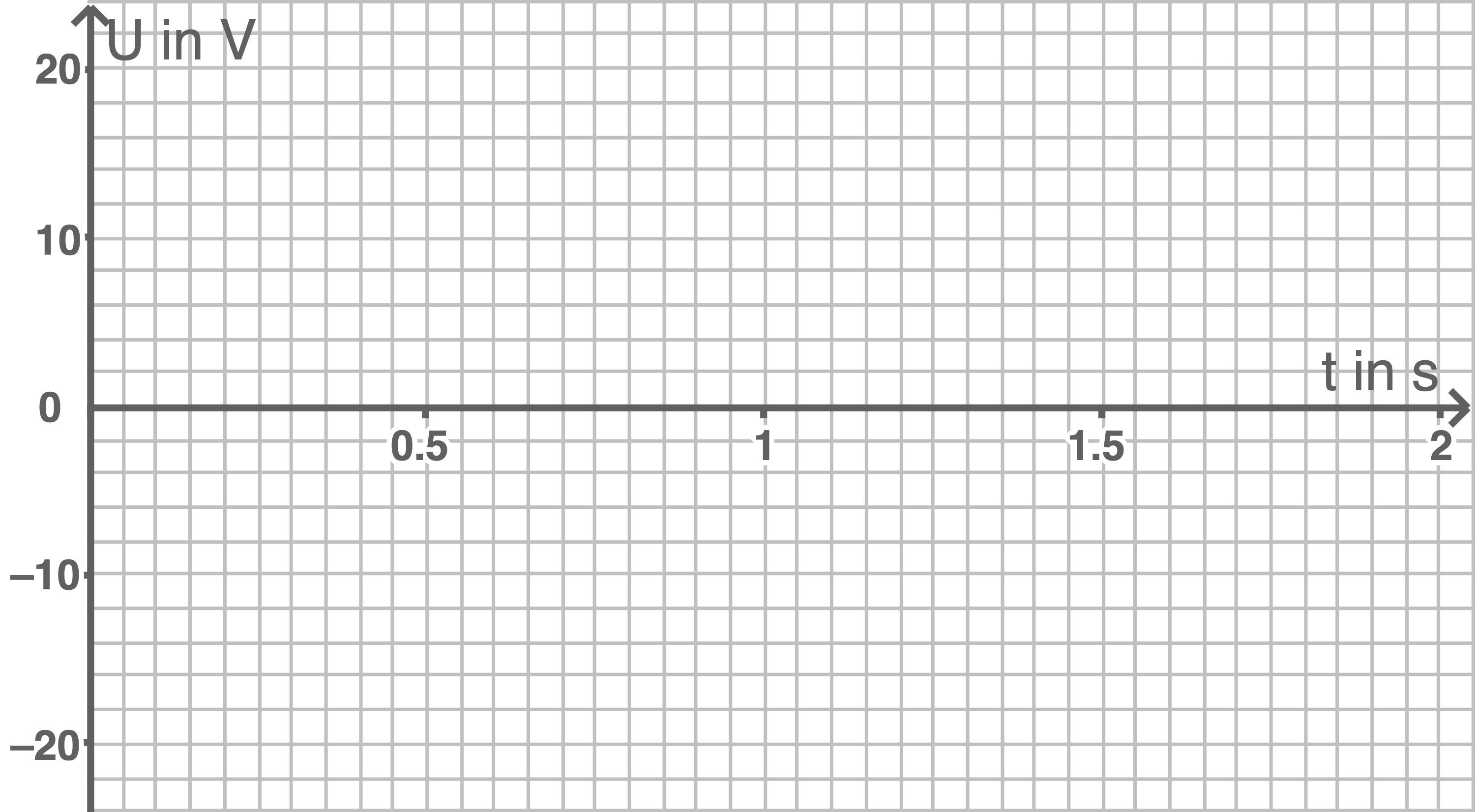

Abbildung 4
(9 VP)
4.
Bei einem Experiment befindet sich ein kleiner Magnet am oberen Ende eines Kunststoffrohrs, das von drei baugleichen Spulen der Länge  umgeben ist (siehe Abbildung 5).
umgeben ist (siehe Abbildung 5).
Zum Zeitpunkt wird der Dauermagnet aus der Ruhe heraus losgelassen. Mit einem Messwerterfassungssystem wird der zeitliche Verlauf der an den Spulen entstehenden Spannung zwischen den Anschlüssen 1 und 2 gemessen.
wird der Dauermagnet aus der Ruhe heraus losgelassen. Mit einem Messwerterfassungssystem wird der zeitliche Verlauf der an den Spulen entstehenden Spannung zwischen den Anschlüssen 1 und 2 gemessen.
Zum Zeitpunkt
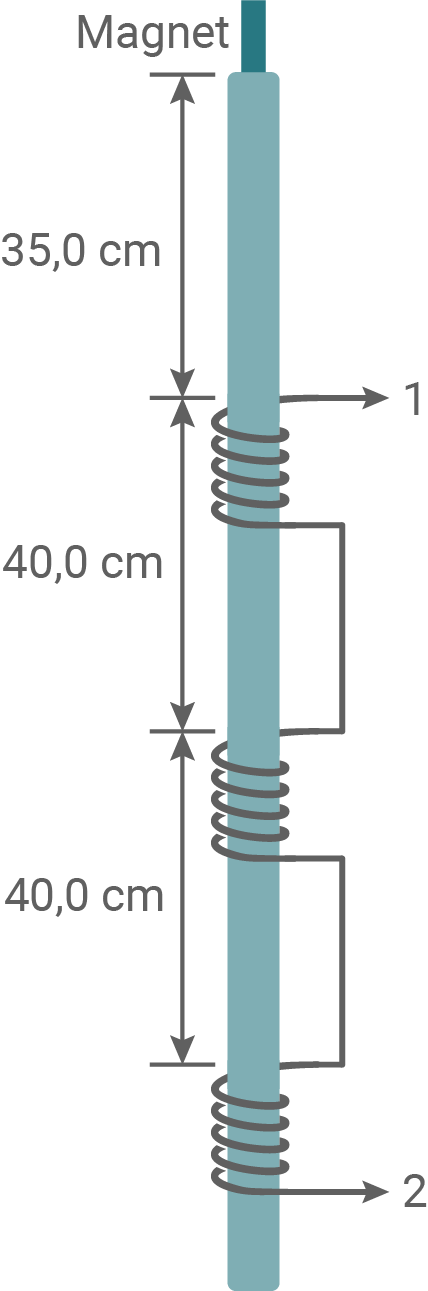
Abbildung 5
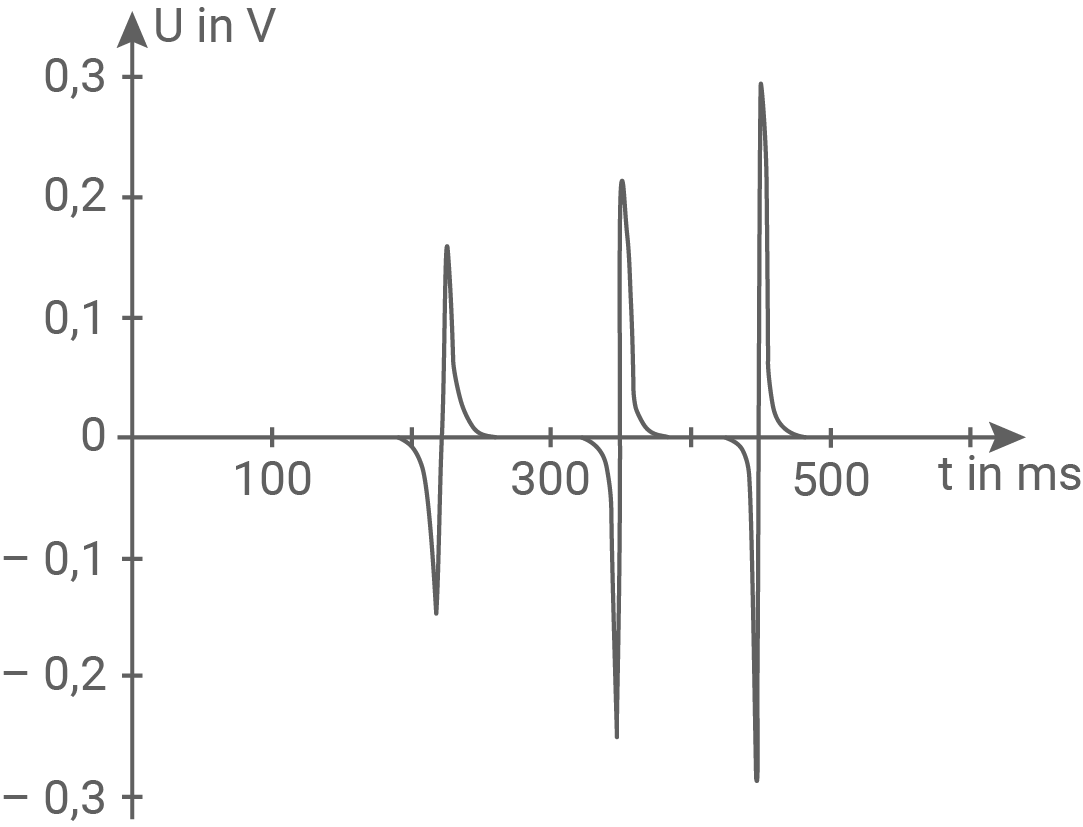
Abbildung 6
a)
Erläutere den Kurvenverlauf im Zeitintervall 
Der gesamte Kurvenverlauf entspricht in einigen charakteristischen Merkmalen den theoretischen Erwartungen.
b)
Nenne zwei solche Merkmale und begründe deine Angabe.
c)
Nenne ein Merkmal, das den theoretischen Erwartungen nicht entspricht, und begründe deine Angabe.
(7 VP)
1
a)
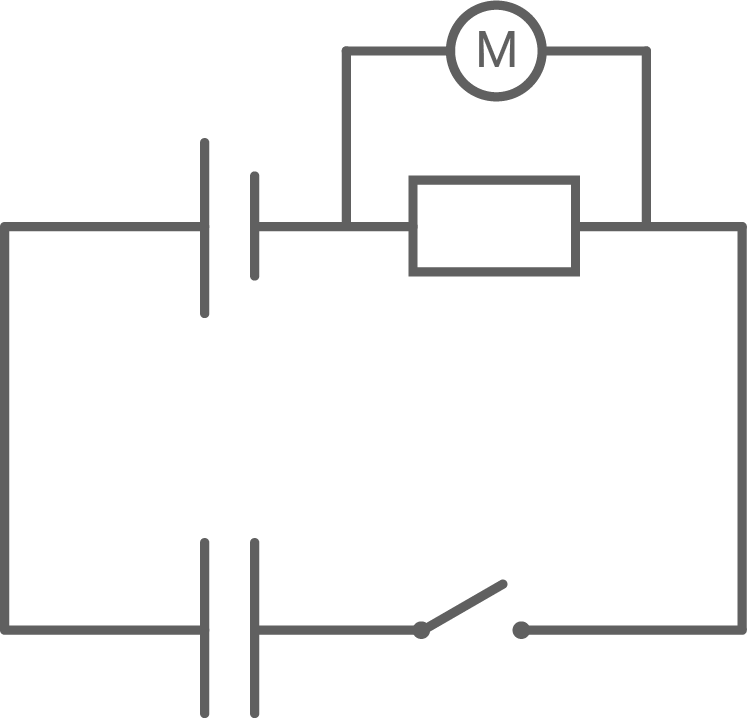
b)
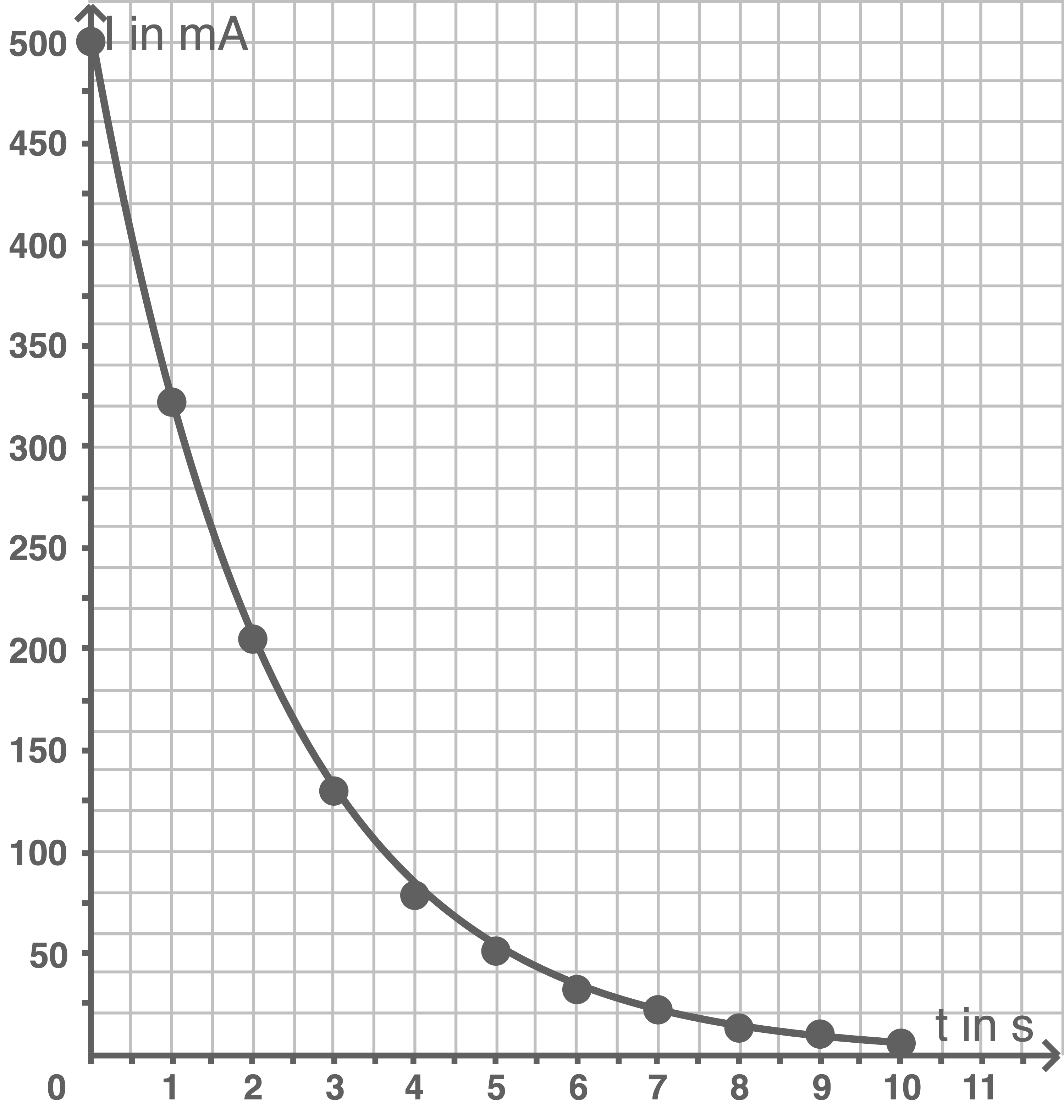
Zeit-Stromstärke-Diagramm
c)
Zum Zeitpunkt  ist der Kondensator ungeladen. Somit fällt an ihm keine Spannung ab. Das heißt, die gesammte Spannung fällt an den Wiederstand ab. Durch das Messwerterfassungssystem ist bekannt, dass die Stromstärke zum diesem Zeitpunkt
ist der Kondensator ungeladen. Somit fällt an ihm keine Spannung ab. Das heißt, die gesammte Spannung fällt an den Wiederstand ab. Durch das Messwerterfassungssystem ist bekannt, dass die Stromstärke zum diesem Zeitpunkt  beträgt. Die Spannung kann wie folgt berechnet werden:
beträgt. Die Spannung kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
U &=& R \cdot I \\[5pt]
U &=& 10,0 \text{ } \Omega \cdot 0,500 \text{ A} \\[5pt]
U &=& 5,00 \text{ V}
\end{array}\)](https://www.schullv.de/resources/formulas/31af61d5f5fc375a936e5ec38d284a021effe7b0f13b1550f882a40d8d49fc1e_light.svg)
d)
Die Kapazität wird mit der in der Aufgabenstellung angegebenen Formel berechnet:
Hinweis zu der Gleichung: Es kann ein beliebiges  aus der Wertetabelle in die Formel eingesetzt werden. Dafür ändern sich jedoch die Werte für
aus der Wertetabelle in die Formel eingesetzt werden. Dafür ändern sich jedoch die Werte für  leicht.
leicht.
e)
1. Schritt: Überlegung
Die Ladungsmenge entspricht dem Flächeninhalt unterhalb der Stromstärkenkurve. Dieser kann entweder durch Kästchen zählen bestimmt werden (ungenau), oder durch das Berechnen des Integrals. Im folgenden wird der zweite Ansatz verfolgt.
2. Schritt: Berechnen der Ladungsmenge in den ersten zwei Minuten
![\(\begin{array}[t]{rll}
\Delta Q &=& \displaystyle\int_{0 \text{ s}}^{2 \text{ s}}I(t)\;\mathrm dt \\[5pt]
\Delta Q &=& \displaystyle\int_{0 \text{ s}}^{2 \text{ s}} I(0 \text{ s}) \cdot \mathrm{e}^{- \frac{1}{R \cdot C} \cdot t} \;\mathrm dt \\[5pt]
\Delta Q &=& \left[ - I(0 \text{ s}) \cdot R \cdot C\cdot \mathrm{e}^{- \frac{1}{R \cdot C} \cdot t} \right]^{2 \text{ s}}_{0 \text{ s}} \\[5pt]
\Delta Q &=& 0,66 \text{ C}
\end{array}\)](https://www.schullv.de/resources/formulas/b30a06546a554f1e9cedaf1ca1568a6beb3cdbeda83a17529e8203e2e7c2d4af_light.svg) 3. Schritt: Berechnen der gesammten Ladungsmenge
Die maximale Ladung kann durch Umstellen der Formel für die Kapazität berechtet werden:
3. Schritt: Berechnen der gesammten Ladungsmenge
Die maximale Ladung kann durch Umstellen der Formel für die Kapazität berechtet werden:
![\(\begin{array}[t]{rll}
C &=& \dfrac{Q_{\text{max}}}{U} &\quad \scriptsize \mid\; \cdot U \\[5pt]
Q_{\text{max}} &=& C \cdot U \\[5pt]
Q_{\text{max}} &=& 0,23 \text{ F} \cdot 5,0 \text{ V} \\[5pt]
Q_{\text{max}} &=& 1,15 \text{ C} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c8c023ae81a647dcad39584a8d1f2ad0e921d7c972b89581584f8a8c90375d06_light.svg) 4. Schritt: Vergleich der beiden Ladungsmengen
Das Verhältniss zwischen der Lagung, die innerhalb der ersten zwei Sekunden auf den Kondensator fließt, und der gesammt Ladung kann wie folgt berechnet werden:
4. Schritt: Vergleich der beiden Ladungsmengen
Das Verhältniss zwischen der Lagung, die innerhalb der ersten zwei Sekunden auf den Kondensator fließt, und der gesammt Ladung kann wie folgt berechnet werden:


 Der Kondensator ist nach 2 Sekunden zu ca.
Der Kondensator ist nach 2 Sekunden zu ca.  aufgeladen.
aufgeladen.
2
a)
Da laut Aufgabenstellung die Potenzialdifferenz konstant ist, können in der Abbildung die Linien gezählt werden, dass dann mit der Liniendifferenzen gerechnet wird.
Es sind insgesammt 5 Äquipotenziallinien eingezeichnet. Somit gibt es 6 Stufen, in denen das Potenzial gleich ansteigt. In einem Stufen steigt das Potenzial um:
 Der Punkt A ist 2 Stufen von der quaderförmigen Elektrode mit dem Potential von
Der Punkt A ist 2 Stufen von der quaderförmigen Elektrode mit dem Potential von  entfernt und sein Potenzial lässt sich wie folgt ausrechnen:
entfernt und sein Potenzial lässt sich wie folgt ausrechnen:


Es sind insgesammt 5 Äquipotenziallinien eingezeichnet. Somit gibt es 6 Stufen, in denen das Potenzial gleich ansteigt. In einem Stufen steigt das Potenzial um:
b)
Um vom Punkt A nach B zu kommen, müssen drei Potenzialstufen überwuden werden. Somit beträgt die Potenzialdifferenz  Ein Proton hat eine Ladung von
Ein Proton hat eine Ladung von  Die benötigte Energie um das Proton von Punkt A nach Punkt B zu verschieben lässt sich mit der folgeneden Formel berechenen:
Die benötigte Energie um das Proton von Punkt A nach Punkt B zu verschieben lässt sich mit der folgeneden Formel berechenen:
![\(\begin{array}[t]{rll}
W &=& q \cdot U \\[5pt]
W &=& 1,60 \cdot 10^{-19} \text{ C} \cdot 4,5 \text{ kV} \\[5pt]
W &=& 7,2 \cdot 10^{-16} \text{ J} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/843209aad0951904ca515e50b64443ef1d5b75cdafbf719b8e0dffe4525b3763_light.svg)
c)
Aus der Wertetabelle kann abgelesen werden, dass sich mit wachsendem Abstand die elektrische Kraft verringert. Somit fallen Zusammenhänge (1), (3) und (5) weg.
Desweiteren lässt sich aus der Tabelle ablesen, dass wenn sich der Abstand von auf
auf  verdoppelt, sich die elektrische Kraft grob viertelt. Somit bleibt nur noch noch Ansatz (4) übrig:
verdoppelt, sich die elektrische Kraft grob viertelt. Somit bleibt nur noch noch Ansatz (4) übrig:
![\(\begin{array}[t]{rll}
F_{\text{el}} &=& \dfrac{k}{r^2} &\quad \scriptsize \mid\; \cdot r^2 \\[5pt]
k &=& F_{\text{el}} \cdot r^2
\end{array}\)](https://www.schullv.de/resources/formulas/705db0422d078b96c2dfdd1b12b581797f8dc73027f64f5019e7aef9e57ba90f_light.svg)
Es ist erkennbar, dass der Wert  annähernd konstant ist. Somit haben die Messwerte Ansatz (4) bestätigt.
annähernd konstant ist. Somit haben die Messwerte Ansatz (4) bestätigt.
Desweiteren lässt sich aus der Tabelle ablesen, dass wenn sich der Abstand von
| 5,00 | 24,5 | 613 |
| 10,00 | 6,05 | 605 |
| 20,0 | 1,52 | 608 |
| 30,0 | 0,68 | 612 |
| 50,0 | 0,24 | 600 |
d)
1. Schritt: Überlegung
Die in der Aufgabenstellung gegebenen Formel muss lediglich nach  umgestellt werden und der Mittelwert der
umgestellt werden und der Mittelwert der  aus Aufgabenteil c) muss eingesetzt werden.
2. Schritt: Berechnung des Durchschnitts von
aus Aufgabenteil c) muss eingesetzt werden.
2. Schritt: Berechnung des Durchschnitts von  Der Durchschnitt von
Der Durchschnitt von  wird mit den Messwerten aus c) bestimmt:
3. Schritt: Berechnung der Ladungsmenge
wird mit den Messwerten aus c) bestimmt:
3. Schritt: Berechnung der Ladungsmenge 
3
a)
Wenn der Schalter geschlossen wird, beginnt der Stromfluss anzusteigen. Der Strom fließt sowohl durch den Zweig mit dem Widerstand als auch durch den Zweig mit der Spule. In dem Zweig mit dem Widerstand fängt die Lampe sofort an zu Leuchten. In dem Zweig mit der Spule beginnt die Lampe erst später zu leuchten.
Wenn in einer Spule die Stromstärke anfängt zu steigen, so baut sich in dieser ein Magnetfeld auf. Dieses ist nach der Lenzischen Regel seiner Ursache, also dem ansteigenedem Strommfluss entgegengerichtet. Somit wird in die Spule eine Spannung induziert, die dem ansteigenedem Strommfluss entgegenwirkt. Aufgrunddessen steigt die tatsächliche Stromstärke merklich langsamer, als die in dem Zweig mit dem Widerstand.
b)
Wird der Schalter geöffnet, besteht der Stromkreis nur noch aus den zwei Zweigen. Die Lämpchen sind nun also in Reihe geschaltet. Die Stromstärke nimmt nicht sofort ab, da die Eigeninduktion der Spule den Abstieg verlangsamt. Somit gehen die Lämpchen, die in Reihe liegen, merklich nach dem Öffnen des Schalters gleichzeitig aus.
c)
Die einzige Spannung, die nach dem Öffnen des Schalters anliegt, ist die von der Spule induzierte Spannung. Diese wird durch folgende Formel beschrieben:
 Diese Spannung kann auch durch die bekannte Formel
Diese Spannung kann auch durch die bekannte Formel  ausgedrückt werden. Der Gesamtwiderstand
ausgedrückt werden. Der Gesamtwiderstand  des Stromkreises beträgt
des Stromkreises beträgt 
 Der Widerstand der Spule beträgt
Der Widerstand der Spule beträgt  und der Widerstand einer Lampe beträgt
und der Widerstand einer Lampe beträgt  Somit beträgt der Widerstand
Somit beträgt der Widerstand  des zweiten Zweige
des zweiten Zweige  Zum Zeitpunkt des Ausschaltens fließt ein Strom von:
Zum Zeitpunkt des Ausschaltens fließt ein Strom von:
![\(\begin{array}[t]{rll}
I_2 &=& \dfrac{U_0}{R_2} \\[5pt]
I_2 &=& \dfrac{10 \text{ V}}{100 \; \Omega} \\[5pt]
I_2 &=& 0,10 \text{ A}
\end{array}\)](https://www.schullv.de/resources/formulas/bc08d3aaa1d4fcd1f1dbe88522ec7ccc82ddb32383dbec1f3e9c0991e727ef7b_light.svg) Somit beträgt die induzierte Spannung:
Somit beträgt die induzierte Spannung:
![\(\begin{array}[t]{rll}
U_{\text{ind}} &=& U \\[5pt]
U_{\text{ind}} &=& R_{\text{ges}} \cdot I \\[5pt]
U_{\text{ind}} &=& 200 \; \Omega \cdot 0,10 \text{ A} \\[5pt]
U_{\text{ind}} &=& 20 \text{ V}
\end{array}\)](https://www.schullv.de/resources/formulas/4664173f1148b280a07c11834eb8ba588892e551d29182504dac1916597339c5_light.svg)
d)
1. Schritt: Überlegung
Die induzierte Spannung kann mit folgender Formel berechnet werden:  Die Induktivität der Spule beträgt laut Aufgabenstellung
Die Induktivität der Spule beträgt laut Aufgabenstellung  Die Änderung der Stromstärke kann durch die Steigung der Stromstärkekurve in Abbildung 3 bestimmt werden.
2. Schritt: Ablesen der Stromstärkenänderung
Um die Stromstärkenänderung zu einem Zeitpunkt
Die Änderung der Stromstärke kann durch die Steigung der Stromstärkekurve in Abbildung 3 bestimmt werden.
2. Schritt: Ablesen der Stromstärkenänderung
Um die Stromstärkenänderung zu einem Zeitpunkt  zu bestimmen, muss an der Stelle
zu bestimmen, muss an der Stelle  in dem Schaubild auf dem Graphen eine Tangente angelegt werden. Die Steigung der Tangente entspricht der Änderung der Stromstärke. Es können folgende Stromstärkenänderungen abgelesen werden:
in dem Schaubild auf dem Graphen eine Tangente angelegt werden. Die Steigung der Tangente entspricht der Änderung der Stromstärke. Es können folgende Stromstärkenänderungen abgelesen werden:

 3. Schritt: Berechnung der induzierten Spannung
Berechnen der induzierten Spannung mit der Formel aus dem 1. Schritt und mit den Werten aus dem zweiten Schritt ergibt:
3. Schritt: Berechnung der induzierten Spannung
Berechnen der induzierten Spannung mit der Formel aus dem 1. Schritt und mit den Werten aus dem zweiten Schritt ergibt:
![\(\begin{array}[t]{rll}
U_{\text{ind}}(0,15 \text{ s}) &=& - L \cdot \dot{I}(0,15 \text{ s}) \\[5pt]
U_{\text{ind}}(0,15 \text{ s}) &=& - 20 \text{ H} \cdot 0,23 \; \dfrac{\text{A}}{\text{s}} \\[5pt]
U_{\text{ind}}(0,15 \text{ s}) &=& -4,6 \text{ V} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b254eb88a8bb88d1ff079a86260c029e96e3cd7602bd513f1c11efd4c9eb71b1_light.svg)
![\(\begin{array}[t]{rll}
U_{\text{ind}}(1,15 \text{ s}) &=& - L \cdot \dot{I}(0,15 \text{ s}) \\[5pt]
U_{\text{ind}}(1,15 \text{ s}) &=& - 20 \text{ H} \cdot \left( - 0,22 \; \dfrac{\text{A}}{\text{s}} \right) \\[5pt]
U_{\text{ind}}(1,15 \text{ s}) &=& 4,4 \text{ V} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e6a1ccb36a77b0c51b53450f2ad5f1adce1e03975e41e49c20281e88118a186d_light.svg)
e)
Es sind bereits folgende Wertepaare bekannt:
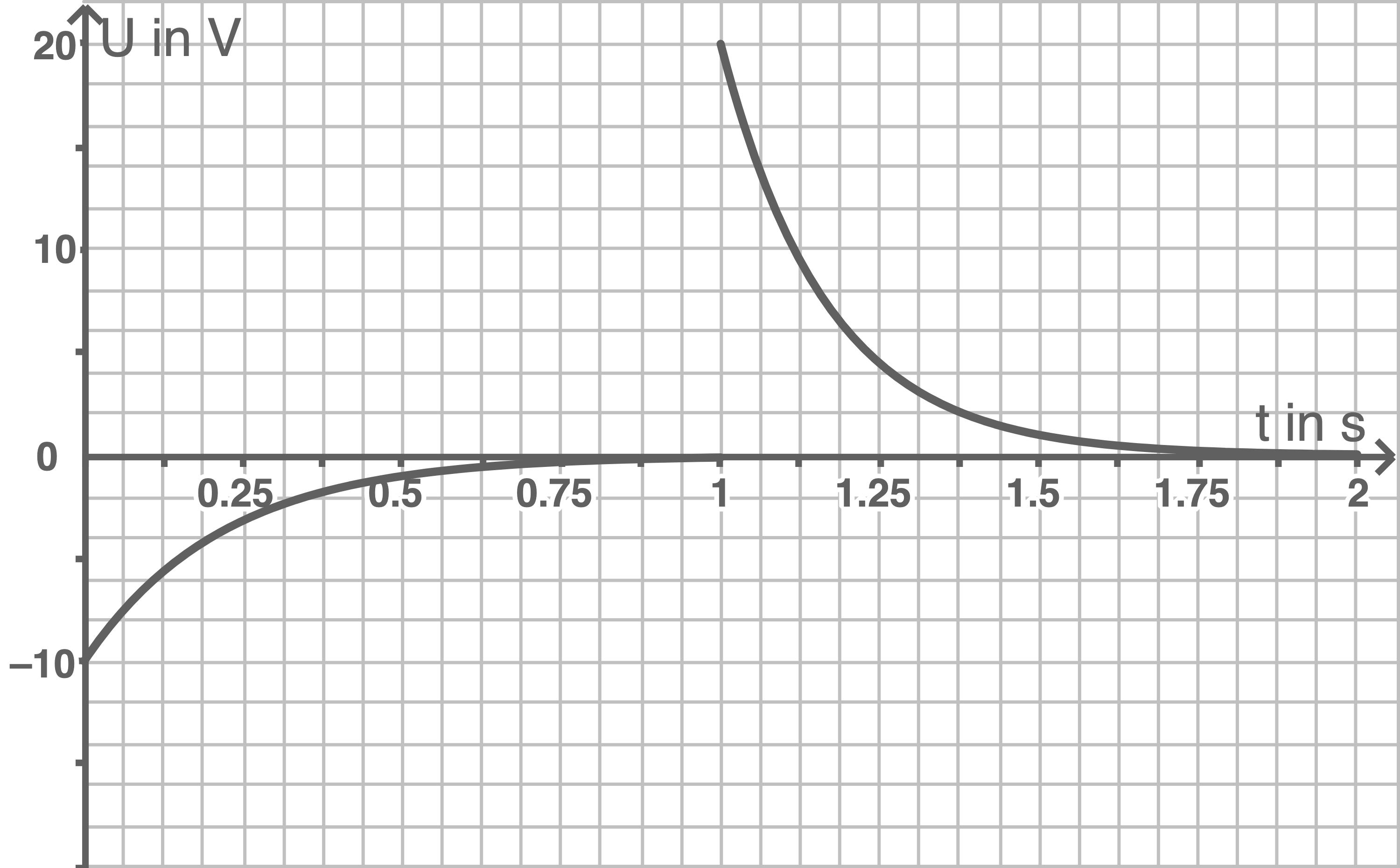
- Wird der Schalter zum Zeitpunkt
geschlossen, dann gilt:
. Da eine Spannung von
anliegt, beträgt die induzierte Spannung
. Somit ist
- Aus Teilaufgabe d) ist folgendes Wertepaar bekannt:
- Aus Abbildung 3 ist ersichtlich, dass zum Zeitpunkt
der Schalter geschlossen wird. Aus Teilaufgabe c) ist somit folgendes Wertepaar bekannt:
- Aus Teilaufgabe d) ist folgendes Wertepaar bekannt:

4
a)
Der Magnet durchquert in diesem Zeitraum die oberste Spule. Der magnetische Fluss nimmt beim Eintreten des Magneten in die Spule zu. Somit wird eine Spannung induziert. Diese vergrössert sich, bis der Magnet bis zu der Mitte der Spule vorgedrungen ist. Nun wechselt das Vorzeichen der Spannung. Der Betrag der Spannung ist jetzt höher, da der Magnet an Geschwindigkeit zugenommen hat. Nun nimmt die Spannung wieder ab und erreicht die Null Volt, wenn der Magnet vollständig aus der Spule ausgetreten ist.
b)
Der Kurvenverlauf zeigt folgende theoretischen Merkmale:
- Das Vorzeichen der Spannung verändert sich beim Durchfliegen einer Spule durch den Magneten.
- Jeder Abschnitt im Diagramm, in dem der Magnet eine Spule durchläuft, muss kleiner werden, da der Magnet immer weniger Zeit benötigt durch eine Spule zu fliegen, da er schneller wird.
- Die Fallzeit des Magneten zwischen einzelnen Spulen mit gleichem Abstand nimmt ab, da der Magnet durch die Gravitation beschleunigt wird.
c)
Der Magnet wird durch die Gravitation durchgehend beschleunigt. Somit nimmt die Geschwindigkeit des Magneten kontinuierlich zu. Somit sollte auch immer der Betrag der induzierten Spannung beim Austritt des Magneten aus einer Spule größer sein, als beim Eintritt in die Spule.
Dies steht im Widerspruch zum Diagramm: Die zweite positive Spannungsspitze ist betragsmäßig kleiner als die zweite negative Spannungsspitze.
Dies steht im Widerspruch zum Diagramm: Die zweite positive Spannungsspitze ist betragsmäßig kleiner als die zweite negative Spannungsspitze.