Aufgabe 1A
Der Sprung eines Fallschirmspringers soll in drei Phasen modelliert werden. In Phase A, beginnend zum Zeitpunkt  , wird der Springer bei geschlossenem Fallschirm immer schneller. In Phase B fällt er aufgrund des Luftwiderstandes mit konstanter Sinkgeschwindigkeit. Mit Öffnen des Fallschirms soll Phase C beginnen, in der der Fallschirm den Springer zunächst deutlich abbremst, so dass er schließlich eine zum Landen geeignete nahezu konstante Sinkgeschwindigkeit erreicht. Während des gesamten Sprungs werden die Höhe in Metern über dem Boden und die Zeit in Sekunden gemessen.
, wird der Springer bei geschlossenem Fallschirm immer schneller. In Phase B fällt er aufgrund des Luftwiderstandes mit konstanter Sinkgeschwindigkeit. Mit Öffnen des Fallschirms soll Phase C beginnen, in der der Fallschirm den Springer zunächst deutlich abbremst, so dass er schließlich eine zum Landen geeignete nahezu konstante Sinkgeschwindigkeit erreicht. Während des gesamten Sprungs werden die Höhe in Metern über dem Boden und die Zeit in Sekunden gemessen.
a) Der Springer misst während der Phase B zum Zeitpunkt  die Höhe
die Höhe  und zum Zeitpunkt
und zum Zeitpunkt  die Höhe
die Höhe  .
Weisen Sie mithilfe dieser Daten nach, dass sich die Höhe des Fallschirmspringers in Abhängigkeit von der Zeit
.
Weisen Sie mithilfe dieser Daten nach, dass sich die Höhe des Fallschirmspringers in Abhängigkeit von der Zeit  im Zeitraum der Phase B durch die Funktion
im Zeitraum der Phase B durch die Funktion  mit
mit  beschreiben lässt.
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion
beschreiben lässt.
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion  mit
mit  modelliert werden. Diese soll zum Zeitpunkt
modelliert werden. Diese soll zum Zeitpunkt  stetig und differenzierbar an
stetig und differenzierbar an  anschließen. Ihr Graph soll durch den Punkt
anschließen. Ihr Graph soll durch den Punkt  verlaufen.
Bestimmen Sie mithilfe dieser Informationen die Funktionsgleichung für
verlaufen.
Bestimmen Sie mithilfe dieser Informationen die Funktionsgleichung für  .
Skizzieren Sie die entsprechenden Graphen für die Phasen A und B bis zum Zeitpunkt
.
Skizzieren Sie die entsprechenden Graphen für die Phasen A und B bis zum Zeitpunkt  und markieren Sie die Grenze zwischen den beiden Phasen.
und markieren Sie die Grenze zwischen den beiden Phasen.
(17P)
b) Nach 16 Sekunden öffnet der Springer den Fallschirm und leitet damit die Phase C ein.
Die Höhe in dieser Phase soll durch die Funktion  mit
mit  modelliert werden.
Berechnen Sie den Zeitpunkt, zu dem der Springer den Boden erreicht.
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von
modelliert werden.
Berechnen Sie den Zeitpunkt, zu dem der Springer den Boden erreicht.
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von  erreichen.
Bestimmen Sie den Zeitpunkt
erreichen.
Bestimmen Sie den Zeitpunkt  , zu dem eine Geschwindigkeit erreicht wird, die nur noch
, zu dem eine Geschwindigkeit erreicht wird, die nur noch  von dem Richtwert abweicht.
Begründen Sie anhand des Terms der Geschwindigkeitsfunktion, dass ab dem Zeitpunkt
von dem Richtwert abweicht.
Begründen Sie anhand des Terms der Geschwindigkeitsfunktion, dass ab dem Zeitpunkt  die Sinkgeschwindigkeit nicht mehr als
die Sinkgeschwindigkeit nicht mehr als  vom Richtwert abweicht.
vom Richtwert abweicht.
(14P)
c) Unabhängig von der obigen Modellierung kann die Sinkgeschwindigkeit mit Fallschirm auch durch die Funktion  mit
mit  ,
,  in Sekunden,
in Sekunden,  in Metern pro Sekunde, beschrieben werden.
Zeigen Sie, dass diese Funktion die Differentialgleichung des begrenzten Wachstums
in Metern pro Sekunde, beschrieben werden.
Zeigen Sie, dass diese Funktion die Differentialgleichung des begrenzten Wachstums
 , mit
, mit  , für geeignete Werte von
, für geeignete Werte von  und
und  erfüllt.
Klassifizieren Sie die Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang, indem Sie die Vorzeichen der Parameter
erfüllt.
Klassifizieren Sie die Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang, indem Sie die Vorzeichen der Parameter  und
und  variieren.
variieren.
(15P)
(46P)
a)  Funktionsterm für Phase B überprüfen
Der Springer misst während der Phase B zum Zeitpunkt
Funktionsterm für Phase B überprüfen
Der Springer misst während der Phase B zum Zeitpunkt  die Höhe
die Höhe  und zum Zeitpunkt
und zum Zeitpunkt  die Höhe
die Höhe  .
Um zu überprüfen, ob Phase B durch die gegebene Gerade modelliert wird, deren Form gegeben ist durch
.
Um zu überprüfen, ob Phase B durch die gegebene Gerade modelliert wird, deren Form gegeben ist durch  , setze die oben angegebenen Bedingungen ein.
, setze die oben angegebenen Bedingungen ein.
 Beide Bedingungen sind erfüllt, Phase B kann also durch
Beide Bedingungen sind erfüllt, Phase B kann also durch  modelliert werden.
modelliert werden.
 Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion
Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion  mit
mit  modelliert werden. Diese soll zum Zeitpunkt
modelliert werden. Diese soll zum Zeitpunkt  stetig und differenzierbar an
stetig und differenzierbar an  anschließen. Das bedeutet, dass die beiden Funktionen für
anschließen. Das bedeutet, dass die beiden Funktionen für  den gleichen Funktionswert haben, es gilt also
den gleichen Funktionswert haben, es gilt also  :
:
 Der Graph von
Der Graph von  verläuft also durch den Punkt
verläuft also durch den Punkt  .
Der Übergang soll stetig und differenzierbar sein, das bedeutet, dass die Graphen der Funktionen in
.
Der Übergang soll stetig und differenzierbar sein, das bedeutet, dass die Graphen der Funktionen in  die gleiche Steigung haben müssen, es gilt also
die gleiche Steigung haben müssen, es gilt also  :
:
 mit
mit  Für die Ableitung von
Für die Ableitung von  gilt also
gilt also  .
Der Graph soll außerdem durch den Punkt
.
Der Graph soll außerdem durch den Punkt  verlaufen.
Du hast nun 3 Bedingungen um den Funktionsterm für
verlaufen.
Du hast nun 3 Bedingungen um den Funktionsterm für  bestimmen zu können.
1. Bedingung:
bestimmen zu können.
1. Bedingung:  2. Bedingung:
2. Bedingung:  3. Bedingung:
3. Bedingung:  Definiere dir die Funktion und deren Ableitung in deinem Taschenrechner und löse dann das lineare Gleichungssystem.
menu:
Definiere dir die Funktion und deren Ableitung in deinem Taschenrechner und löse dann das lineare Gleichungssystem.
menu:  3:
3:  7:
7:  1:
1:
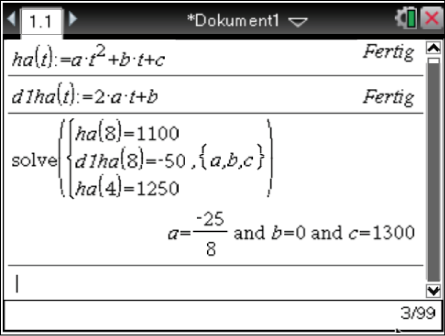 Für die gesuchten Parameter gilt
Für die gesuchten Parameter gilt  ,
,  und
und  .
Die Funktionsgleichung für
.
Die Funktionsgleichung für  ist gegeben durch
ist gegeben durch  .
.
 Skizze der Phase A und B
Du kannst Phase A und B skizzieren, indem du dir vor Augen führst welche Form die jeweiligen Funktionsterme haben:
Skizze der Phase A und B
Du kannst Phase A und B skizzieren, indem du dir vor Augen führst welche Form die jeweiligen Funktionsterme haben:
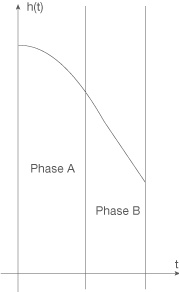

- Phase A: Der Graph, der Phase A beschreibt ist die rechte Hälfte einer nach unten geöffneten Parabel, da die zugehörige Funktion zweiten Grades ist und einen negativen Höchstkoeffizienten besitzt.
- Phase B: Der Graph, der Phase B beschreibt ist eine fallende Gerade, die am Übergang direkt an den Graphen von Phase A anschließt. Zudem liegt die Nullstelle dieses Graphen nicht innerhalb des Intervalls, indem Phase B liegt.

b)  Zeitpunkt der Landung berechnen
Die Höhe in dieser Phase wird durch
Zeitpunkt der Landung berechnen
Die Höhe in dieser Phase wird durch  modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Taschenrechner ein und berechne die Nullstelle.
modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Taschenrechner ein und berechne die Nullstelle.
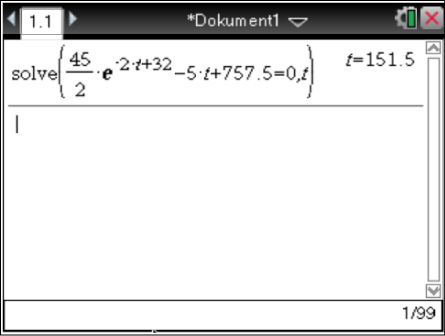 Die Nullstelle ist gegeben durch
Die Nullstelle ist gegeben durch  , somit ist der Zeitpunkt der Landung nach
, somit ist der Zeitpunkt der Landung nach  Sekunden .
Sekunden .
 Zeitpunkt für Erreichen des zulässigen Bereichs der Landegeschwindigkeit
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von
Zeitpunkt für Erreichen des zulässigen Bereichs der Landegeschwindigkeit
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von  erreichen. Du sollst den Zeitpunkt
erreichen. Du sollst den Zeitpunkt  bestimmen, zu dem eine Geschwindigkeit erreicht wird, die nur noch
bestimmen, zu dem eine Geschwindigkeit erreicht wird, die nur noch  von dem Richtwert abweicht.
Um die Funktion der Sinkgeschwindigkeit zu erhalten, leite die Funktion
von dem Richtwert abweicht.
Um die Funktion der Sinkgeschwindigkeit zu erhalten, leite die Funktion  ab:
ab:
 Für den zulässigen Bereich muss
Für den zulässigen Bereich muss  erfüllt sein:
Definiere dir die Funktion
erfüllt sein:
Definiere dir die Funktion  und nutze den solve-Befehl und die Ableitung um den gesuchten Zeitpunkt
und nutze den solve-Befehl und die Ableitung um den gesuchten Zeitpunkt  zu ermitteln. Die Ableitung erhältst du mit
menu:
zu ermitteln. Die Ableitung erhältst du mit
menu:  4:
4:  1:
1:
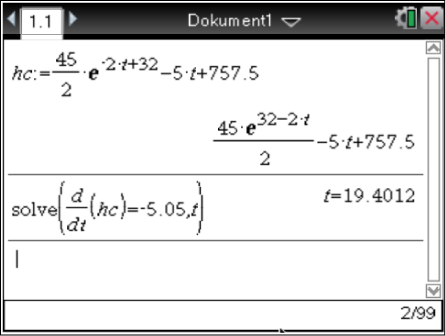 Der Zeitpunkt
Der Zeitpunkt  , zu dem eine Geschwindigkeit erreicht wird, die nur noch 0,05 m/s von dem Richtwert abweicht, ist gegeben durch
, zu dem eine Geschwindigkeit erreicht wird, die nur noch 0,05 m/s von dem Richtwert abweicht, ist gegeben durch  s.
s.
 Begründung für Abweichung vom Richtwert
Der Grenzwert der Geschwindigkeitsfunktion ist -5, da der Exponent für größer werdende
Begründung für Abweichung vom Richtwert
Der Grenzwert der Geschwindigkeitsfunktion ist -5, da der Exponent für größer werdende  gegen
gegen  läuft, somit gilt für
läuft, somit gilt für  . Die Ableitung der Geschwindigkeitsfunktion ist gegeben durch:
. Die Ableitung der Geschwindigkeitsfunktion ist gegeben durch:
 Da die Ableitung für alle
Da die Ableitung für alle  positiv ist, ist die Geschwindigkeitsfunktion streng monoton steigend. Der Geschwindigkeitswert kann somit nicht mehr unter den Wert
positiv ist, ist die Geschwindigkeitsfunktion streng monoton steigend. Der Geschwindigkeitswert kann somit nicht mehr unter den Wert  sinken.
Die Abweichung bleibt somit im geforderten Bereich.
sinken.
Die Abweichung bleibt somit im geforderten Bereich.


c)  Parameter der Differentialgleichung bestimmen
Du hast die Funktion
Parameter der Differentialgleichung bestimmen
Du hast die Funktion  (
( in Sekunden,
in Sekunden,  in Metern pro Sekunde) und deren Ableitung
in Metern pro Sekunde) und deren Ableitung  gegeben. Du sollst zeigen, dass diese Funktion die Differentialgleichung des begrenzten Wachstums
gegeben. Du sollst zeigen, dass diese Funktion die Differentialgleichung des begrenzten Wachstums  , mit
, mit  , für geeignete Werte von
, für geeignete Werte von  und
und  erfüllt.
Setze die beiden Funktionen in die Differentialgleichung ein und bestimme
erfüllt.
Setze die beiden Funktionen in die Differentialgleichung ein und bestimme  und
und  durch Koeffizientenvergleich.
durch Koeffizientenvergleich.
 Jetzt muss gelten:
Jetzt muss gelten:
 Weiter muss gelten:
Weiter muss gelten:
 Die Funktion
Die Funktion  erfüllt die Differentialgleichung des begrenzten Wachstums mit den Parametern
erfüllt die Differentialgleichung des begrenzten Wachstums mit den Parametern  .
.
 Lösungen der Differentialgleichung klassifizieren
Du sollst den Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang klassifizieren, indem du die Vorzeichen der Parameter
Lösungen der Differentialgleichung klassifizieren
Du sollst den Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang klassifizieren, indem du die Vorzeichen der Parameter  und
und  variierst.
Betrachte zuerst den Parameter
variierst.
Betrachte zuerst den Parameter  , der den Grenzwert des Graphen in
, der den Grenzwert des Graphen in  -Richtung verschiebt:
-Richtung verschiebt:
 , dieser entspricht der Wachstumskonstanten. Der Graph hat eine Asymptote, der er sich annähert, da es sich um begrenztes Wachstum handelt.
, dieser entspricht der Wachstumskonstanten. Der Graph hat eine Asymptote, der er sich annähert, da es sich um begrenztes Wachstum handelt.
: Der Grenzwert liegt oberhalb der
-Achse.
: Der Grenzwert liegt unterhalb der
-Achse.
: Der Graph nähert sich für
der Asymptote.
: Der Graph nähert sich für
der Asymptote.
a)  Funktionsterm für Phase B überprüfen
Der Springer misst während der Phase B zum Zeitpunkt
Funktionsterm für Phase B überprüfen
Der Springer misst während der Phase B zum Zeitpunkt  die Höhe
die Höhe  und zum Zeitpunkt
und zum Zeitpunkt  die Höhe
die Höhe  .
Um zu überprüfen, ob Phase B durch die gegebene Gerade modelliert wird, deren Form gegeben ist durch
.
Um zu überprüfen, ob Phase B durch die gegebene Gerade modelliert wird, deren Form gegeben ist durch  , setze die oben angegebenen Bedingungen ein.
, setze die oben angegebenen Bedingungen ein.
 Beide Bedingungen sind erfüllt, Phase B kann also durch
Beide Bedingungen sind erfüllt, Phase B kann also durch  modelliert werden.
modelliert werden.
 Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion
Quadratische Funktion für Höhe des Fallschirmspringers in Phase A bestimmen
Die Höhe des Fallschirmspringers in Phase A soll näherungsweise durch eine quadratische Funktion  mit
mit  modelliert werden. Diese soll zum Zeitpunkt
modelliert werden. Diese soll zum Zeitpunkt  stetig und differenzierbar an
stetig und differenzierbar an  anschließen. Das bedeutet, dass die beiden Funktionen für
anschließen. Das bedeutet, dass die beiden Funktionen für  den gleichen Funktionswert haben, es gilt also
den gleichen Funktionswert haben, es gilt also  :
:
 Der Graph von
Der Graph von  verläuft also durch den Punkt
verläuft also durch den Punkt  .
Der Übergang soll stetig und differenzierbar sein, das bedeutet, dass die Graphen der Funktionen in
.
Der Übergang soll stetig und differenzierbar sein, das bedeutet, dass die Graphen der Funktionen in  die gleiche Steigung haben müssen, es gilt also
die gleiche Steigung haben müssen, es gilt also  :
:
 mit
mit  Für die Ableitung von
Für die Ableitung von  gilt also
gilt also  .
Der Graph soll außerdem durch den Punkt
.
Der Graph soll außerdem durch den Punkt  verlaufen.
Du hast nun 3 Bedingungen um den Funktionsterm für
verlaufen.
Du hast nun 3 Bedingungen um den Funktionsterm für  bestimmen zu können.
1. Bedingung:
bestimmen zu können.
1. Bedingung:  2. Bedingung:
2. Bedingung:  3. Bedingung:
3. Bedingung:  Definiere dir die Funktion und deren Ableitung in deinem Taschenrechner und löse dann das lineare Gleichungssystem.
Den Befehl für eine Ableitung findest du unter
Keyboard
Definiere dir die Funktion und deren Ableitung in deinem Taschenrechner und löse dann das lineare Gleichungssystem.
Den Befehl für eine Ableitung findest du unter
Keyboard  2D
2D  CALC
Den Befehl für ein Gleichungssystem findest du unter
Keyboard
CALC
Den Befehl für ein Gleichungssystem findest du unter
Keyboard  2D
2D
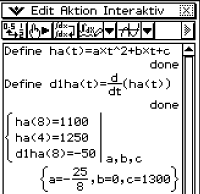 Für die gesuchten Parameter gilt
Für die gesuchten Parameter gilt  ,
,  und
und  .
Die Funktionsgleichung für
.
Die Funktionsgleichung für  ist gegeben durch
ist gegeben durch  .
.
 Skizze der Phase A und B
Du kannst Phase A und B skizzieren, indem du dir vor Augen führst welche Form die jeweiligen Funktionsterme haben:
Skizze der Phase A und B
Du kannst Phase A und B skizzieren, indem du dir vor Augen führst welche Form die jeweiligen Funktionsterme haben:


- Phase A: Der Graph, der Phase A beschreibt ist die rechte Hälfte einer nach unten geöffneten Parabel, da die zugehörige Funktion zweiten Grades ist und einen negativen Höchstkoeffizienten besitzt.
- Phase B: Der Graph, der Phase B beschreibt ist eine fallende Gerade, die am Übergang direkt an den Graphen von Phase A anschließt. Zudem liegt die Nullstelle dieses Graphen nicht innerhalb des Intervalls, indem Phase B liegt.

b)  Zeitpunkt der Landung berechnen
Die Höhe in dieser Phase wird durch
Zeitpunkt der Landung berechnen
Die Höhe in dieser Phase wird durch  modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Taschenrechner ein und berechne die Nullstelle mit dem solve-Befehl des CAS.
modelliert.
Du sollst den Zeitpunkt, zu dem der Springer den Boden erreicht, berechnen. Gib die Funktion in deinen Taschenrechner ein und berechne die Nullstelle mit dem solve-Befehl des CAS.
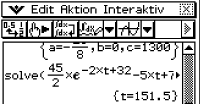 Die Nullstelle ist gegeben durch
Die Nullstelle ist gegeben durch  , somit ist der Zeitpunkt der Landung nach
, somit ist der Zeitpunkt der Landung nach  Sekunden .
Sekunden .
 Zeitpunkt für Erreichen des zulässigen Bereichs der Landegeschwindigkeit
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von
Zeitpunkt für Erreichen des zulässigen Bereichs der Landegeschwindigkeit
Für eine sichere Landung sollte die Sinkgeschwindigkeit in etwa den Richtwert von  erreichen. Du sollst den Zeitpunkt
erreichen. Du sollst den Zeitpunkt  bestimmen, zu dem eine Geschwindigkeit erreicht wird, die nur noch
bestimmen, zu dem eine Geschwindigkeit erreicht wird, die nur noch  von dem Richtwert abweicht.
Um die Funktion der Sinkgeschwindigkeit zu erhalten, leite die Funktion
von dem Richtwert abweicht.
Um die Funktion der Sinkgeschwindigkeit zu erhalten, leite die Funktion  ab:
ab:
 Für den zulässigen Bereich muss
Für den zulässigen Bereich muss  erfüllt sein:
Definiere dir die Funktion
erfüllt sein:
Definiere dir die Funktion  und
und  mit dem Define-Befehl und nutze den solve-Befehl um den gesuchten Zeitpunkt
mit dem Define-Befehl und nutze den solve-Befehl um den gesuchten Zeitpunkt  zu ermitteln.
zu ermitteln.
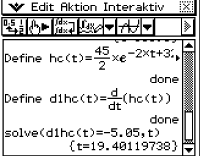 Der Zeitpunkt
Der Zeitpunkt  , zu dem eine Geschwindigkeit erreicht wird, die nur noch 0,05 m/s von dem Richtwert abweicht, ist gegeben durch
, zu dem eine Geschwindigkeit erreicht wird, die nur noch 0,05 m/s von dem Richtwert abweicht, ist gegeben durch  s.
s.
 Begründung für Abweichung vom Richtwert
Der Grenzwert der Geschwindigkeitsfunktion ist -5, da der Exponent für größer werdende
Begründung für Abweichung vom Richtwert
Der Grenzwert der Geschwindigkeitsfunktion ist -5, da der Exponent für größer werdende  gegen
gegen  läuft, somit gilt für
läuft, somit gilt für  . Die Ableitung der Geschwindigkeitsfunktion ist gegeben durch:
. Die Ableitung der Geschwindigkeitsfunktion ist gegeben durch:
 Da die Ableitung für alle
Da die Ableitung für alle  positiv ist, ist die Geschwindigkeitsfunktion streng monoton steigend. Der Geschwindigkeitswert kann somit nicht mehr unter den Wert
positiv ist, ist die Geschwindigkeitsfunktion streng monoton steigend. Der Geschwindigkeitswert kann somit nicht mehr unter den Wert  sinken.
Die Abweichung bleibt somit im geforderten Bereich.
sinken.
Die Abweichung bleibt somit im geforderten Bereich.


c)  Parameter der Differentialgleichung bestimmen
Du hast die Funktion
Parameter der Differentialgleichung bestimmen
Du hast die Funktion  (
( in Sekunden,
in Sekunden,  in Metern pro Sekunde) und deren Ableitung
in Metern pro Sekunde) und deren Ableitung  gegeben. Du sollst zeigen, dass diese Funktion die Differentialgleichung des begrenzten Wachstums
gegeben. Du sollst zeigen, dass diese Funktion die Differentialgleichung des begrenzten Wachstums  , mit
, mit  , für geeignete Werte von
, für geeignete Werte von  und
und  erfüllt.
Setze die beiden Funktionen in die Differentialgleichung ein und bestimme
erfüllt.
Setze die beiden Funktionen in die Differentialgleichung ein und bestimme  und
und  durch Koeffizientenvergleich.
durch Koeffizientenvergleich.
 Jetzt muss gelten:
Jetzt muss gelten:
 Weiter muss gelten:
Weiter muss gelten:
 Die Funktion
Die Funktion  erfüllt die Differentialgleichung des begrenzten Wachstums mit den Parametern
erfüllt die Differentialgleichung des begrenzten Wachstums mit den Parametern  .
.
 Lösungen der Differentialgleichung klassifizieren
Du sollst den Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang klassifizieren, indem du die Vorzeichen der Parameter
Lösungen der Differentialgleichung klassifizieren
Du sollst den Graphen der Lösungen der Differentialgleichung unabhängig von dem Sachzusammenhang klassifizieren, indem du die Vorzeichen der Parameter  und
und  variierst.
Betrachte zuerst den Parameter
variierst.
Betrachte zuerst den Parameter  , der den Grenzwert des Graphen in
, der den Grenzwert des Graphen in  -Richtung verschiebt:
-Richtung verschiebt:
 , dieser entspricht der Wachstumskonstanten. Der Graph hat eine Asymptote, der er sich annähert, da es sich um begrenztes Wachstum handelt.
, dieser entspricht der Wachstumskonstanten. Der Graph hat eine Asymptote, der er sich annähert, da es sich um begrenztes Wachstum handelt.
: Der Grenzwert liegt oberhalb der
-Achse.
: Der Grenzwert liegt unterhalb der
-Achse.
: Der Graph nähert sich für
der Asymptote.
: Der Graph nähert sich für
der Asymptote.