Aufgabe 3A
Aufgabe 3A
Ein Betrieb stellt Fruchtgummi aus der Grundsubstanz| Z1 | Z2 | Z3 | |
|---|---|---|---|
| R1 | 13 | 12 | 12 |
| R2 | 3 | 2 | 2 |
| R3 | 0 | 1 | 3 |
| R4 | 2 | 3 | 1 |
| E1 | E2 | |
|---|---|---|
| Z1 | a | 16 |
| Z2 | 20 | b |
| Z3 | 15 | 17 |
 Abb. 1: Produktionsprozess
Abb. 1: Produktionsprozess
a)
Gib die fehlenden Werte für  und
und  aus Tabelle
aus Tabelle  an.
an.
Erläutere die Bedeutung des Eintrags in Tabelle
in Tabelle  im Sachzusammenhang.
im Sachzusammenhang.
Im Lager befinden sich noch ME der Grundsubstanz
ME der Grundsubstanz  ,
,  ME des Fruchtsaftkonzentrats
ME des Fruchtsaftkonzentrats  und
und  Stück der Fruchtgummitiere
Stück der Fruchtgummitiere  . Es sollen
. Es sollen  Tüten des Sortiments
Tüten des Sortiments  und
und  Tüten des Sortiments
Tüten des Sortiments  produziert werden. Dabei sollen alle vorhandenen Materialien vollständig verwendet werden.
produziert werden. Dabei sollen alle vorhandenen Materialien vollständig verwendet werden.
Bestimme die ME der Grundsubstanz und die ME aller Fruchtsaftkonzentrate, die für diese Produktion nachbestellt werden müssen.
Erläutere die Bedeutung des Eintrags
Im Lager befinden sich noch
Bestimme die ME der Grundsubstanz und die ME aller Fruchtsaftkonzentrate, die für diese Produktion nachbestellt werden müssen.
(9P)
b)
Bisher wurden von den Tüten der Sortimente  und
und  gleich viele produziert. Die Produktion der Tüten des Sortiments
gleich viele produziert. Die Produktion der Tüten des Sortiments  soll um
soll um  und die Produktion der Tüten von Sortiment
und die Produktion der Tüten von Sortiment  soll um
soll um  gesteigert werden.
gesteigert werden.
Berechne, um wie viel Prozent der Bedarf für das Fruchtsaftkonzentrat steigt.
steigt.
Eine Tüte eines neuen Sortiments soll unter folgenden Bedingungen zusammengestellt werden:
soll unter folgenden Bedingungen zusammengestellt werden:
 unter diesen Bedingungen zusammengestellt werden kann.
unter diesen Bedingungen zusammengestellt werden kann.
Berechne, um wie viel Prozent der Bedarf für das Fruchtsaftkonzentrat
Eine Tüte eines neuen Sortiments
- Sie enthält insgesamt
Stück der Fruchtgummitiere
,
und
,
- es werden genau
ME des Fruchtsaftkonzentrats
und
ME des Fruchtsaftkonzentrats
verwendet,
- von der Grundsubstanz
und dem Fruchtsaftkonzentrat
stehen beliebig viele ME zur Verfügung.
(5P)
c)
Unabhängig vom Sachzusammenhang sind die Vektoren  mit
mit  gegeben.
gegeben.
Bestimme alle Vektoren , die die folgende Gleichung lösen:
, die die folgende Gleichung lösen:  .
.
Damit mit
mit  Lösungen hat, müssen
Lösungen hat, müssen  unabhängig von
unabhängig von  und
und  eine Bedingung erfüllen, die als Gleichung formuliert werden kann.
eine Bedingung erfüllen, die als Gleichung formuliert werden kann.
Leite diese Gleichung her. Dokumentiere hierzu einen Lösungsweg, der ohne den Einsatz des Rechners nachvollziehbar ist.
Bestimme alle Vektoren
Damit
Leite diese Gleichung her. Dokumentiere hierzu einen Lösungsweg, der ohne den Einsatz des Rechners nachvollziehbar ist.
(7P)
Bildnachweise [nach oben]
© 2016 - SchulLV.
Aufgabe 3A
a)
| Grundsubstanz |
|
| Fruchtsaftkonzentrat |
|
| Fruchtgummitiere |
b)
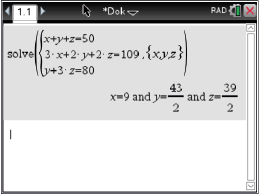 Abb. 1: lineares Gleichungssystem lösen
Abb. 1: lineares Gleichungssystem lösen
c)
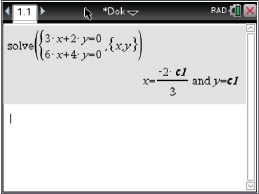 Abb. 2: lineares Gleichungssystem lösen
Abb. 2: lineares Gleichungssystem lösen
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabe 3A
a)
| Grundsubstanz |
|
| Fruchtsaftkonzentrat |
|
| Fruchtgummitiere |
b)
 Abb. 1: lineares Gleichungssystem lösen
Abb. 1: lineares Gleichungssystem lösen
c)
 Abb. 2: lineares Gleichungssystem lösen
Abb. 2: lineares Gleichungssystem lösen
© 2016 - SchulLV.
© 2016 - SchulLV.