Aufgabe 3A
Auf einem ebenen, horizontalen Gelände steht ein 
hoher Mast, an dem drei rechteckige Werbeflächen befestigt sind. In der Abbildung 1 ist eine der Werbeflächen grau dargestellt.
Der Mast ist zylinderförmig und hat einen Durchmesser von 
Er verläuft ebenso wie die seitlichen Kanten der Werbeflächen vertikal.
In einem Koordinatensystem wird das Gelände durch die 
-Ebene beschrieben; eine Längeneinheit im Koordinatensystem entspricht 
in der Wirklichkeit.
Der Mittelpunkt der Grundfläche des Masts wird durch den Koordinatenursprung dargestellt. Die Punkte 
und 
stellen Eckpunkte der Werbeflächen dar.
hoher Mast, an dem drei rechteckige Werbeflächen befestigt sind. In der Abbildung 1 ist eine der Werbeflächen grau dargestellt.
Der Mast ist zylinderförmig und hat einen Durchmesser von Er verläuft ebenso wie die seitlichen Kanten der Werbeflächen vertikal.
In einem Koordinatensystem wird das Gelände durch die -Ebene beschrieben; eine Längeneinheit im Koordinatensystem entspricht in der Wirklichkeit.
Der Mittelpunkt der Grundfläche des Masts wird durch den Koordinatenursprung dargestellt. Die Punkte und stellen Eckpunkte der Werbeflächen dar.
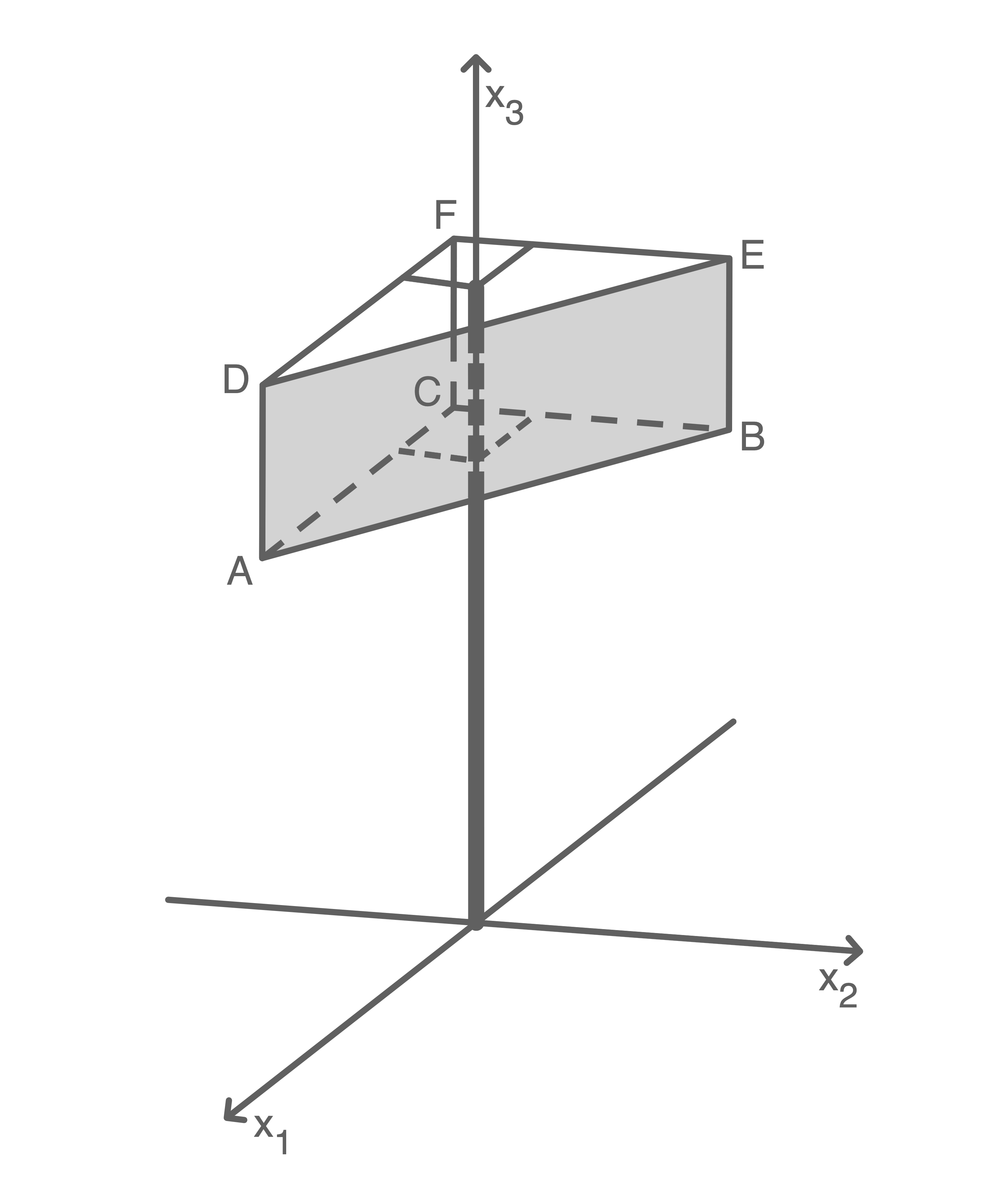
Abbildung 1
a)
Bestimme den Flächeninhalt der grau dargestellten Werbefläche.
Untersuche, ob die beiden anderen Werbeflächen einen rechten Winkel einschließen.
(6 BE)
b)
Die grau dargestellte Werbefläche liegt im Modell in einer Ebene, deren Gleichung in der Form 
dargestellt werden kann.
Ermittle passende Werte von 
und 
dargestellt werden kann.
Ermittle passende Werte von und
(3 BE)
c)
Begründe, dass der Abstand der grau dargestellten Werbefläche zum Mast mit dem Abstand des Mittelpunkts der oberen Kante dieser Werbefläche zum Mast übereinstimmt.
(5 BE)
Auf dem Gelände befindet sich ein Sportplatz. Von dort aus blickt ein Kind zur grau dargestellten Werbefläche. Die Sicht des Kindes wird durch eine Mauer eingeschränkt.
Die obere Kante der Mauer wird durch die Strecke zwischen den Punkten 
und 
dargestellt. Der Punkt, von dem der Blick des Kindes ausgeht, wird durch 
beschrieben.
Das Kind kann denjenigen Teil der Werbefläche, der durch das Dreieck 
mit 
dargestellt wird, nicht sehen (siehe Abbildung 2).
und dargestellt. Der Punkt, von dem der Blick des Kindes ausgeht, wird durch beschrieben.
Das Kind kann denjenigen Teil der Werbefläche, der durch das Dreieck mit dargestellt wird, nicht sehen (siehe Abbildung 2).
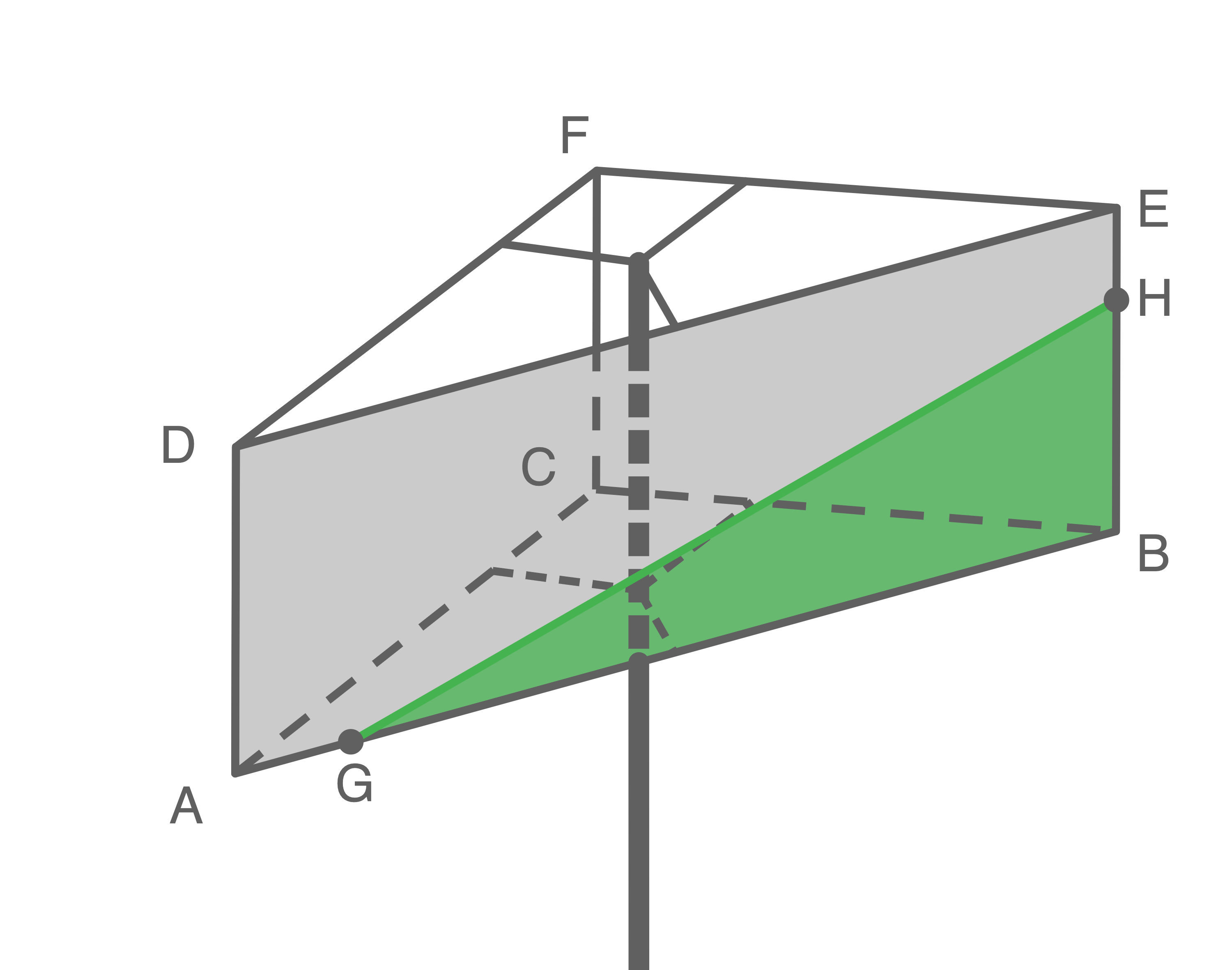
Abbildung 2
d)
Eine Sichtlinie verläuft von 
zu 
Berechne die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände.
zu
Berechne die Größe des Winkels dieser Sichtlinie gegenüber dem horizontalen Gelände.
(3 BE)
e)
Berechne die Koordinaten von 
Auf dem Sportplatz wird ein Fußball geschossen. Die Flugbahn des Balls wird durch Punkte der Form
(5 BE)
mit 
beschrieben. Dabei ist 
die seit dem Schuss vergangene Zeit in Sekunden.
f)
Beschreibe, wie man ermitteln könnte, ob der Ball die Mauer trifft, bevor er den Boden berührt.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Flächeninhalt bestimmen
Der Flächeninhalt der Werbefläche beträgt somit ca. 
Winkel prüfen
Die beiden Werbeflächen schließen somit einen rechten Winkel ein.
![\( A \approx 39,6 \left[\,\text{m}^2\right] \)](https://www.schullv.de/resources/formulas/73f896de125e66fdf52185b80d309140d0afc9c44495eeb86d577df82c2988d4_light.svg)
![\(\begin{array}[t]{rll}
A&=& |\overrightarrow{AB}|\cdot |\overrightarrow{BE}|& \\[5pt]
&=& \left| \pmatrix{-2-5\\5-(-2)\\11-11} \right| \cdot \left| \pmatrix{-2-(-2)\\5-5\\15-11} \right| & \\[5pt]
&=& \sqrt{(-7)^2+7^2+0^2}\cdot \sqrt{0^2+0^2+4^2} & \\[5pt]
&\approx& 39,6 \left[\,\text{m}^2\right]
\end{array}\)](https://www.schullv.de/resources/formulas/0a6499d86573326bba0e51de54f15e8f67a09b5458db171566cfb88c0a44fcc7_light.svg)
Winkel prüfen
Die beiden Werbeflächen schließen somit einen rechten Winkel ein.
![\(\begin{array}[t]{rll}
\overrightarrow{FD}\circ\overrightarrow{FD}&=& \pmatrix{5-(-2)\\-2-(-2)\\15-15}\circ \pmatrix{-2-(-2)\\5-(-2)\\15-15} & \\[5pt]
&=& \pmatrix{7\\0\\0}\circ \pmatrix{0\\7\\0} & \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/674f5165da2e2e0ced3a661b16705a838fbf92f32712cf3f358320d6445d37ef_light.svg)
b)
Einsetzen der Koordinaten von 
in die Ebenengleichung liefert:
![\(\begin{array}[t]{rll}
a\cdot 5+a\cdot (-2)&=& b& \\[5pt]
3a&=& b
\end{array}\)](https://www.schullv.de/resources/formulas/a870d6c55f696768f96e4964e6e63692e57a9bb7378b4c0be2d8d0b9a81009f8_light.svg)
Passende Werte für und 
die diese Gleichung lösen, sind beispielsweise 
und 
in die Ebenengleichung liefert:
Passende Werte für und die diese Gleichung lösen, sind beispielsweise und
c)
Die 
-Achse entspricht der Symmetrieachse des Masts und stellt somit dessen Mittelgerade dar.
Da die Punkte 
und 
den gleichen Abstand zum Punkt 
auf der -Achse haben, ist der Abstand des Mittelpunkts 
der Strecke 
zur -Achse aus Symmetriegründen am kleinsten. Es hat also kein anderer Punkt auf der Strecke einen kleineren Abstand zur -Achse.
Aufgrund des vertikalen Verlaufs der Seitenkanten 
und 
gilt dies für alle weiteren Punkte innerhalb des Vierecks 
Diejenigen Punkte, die vertikal unterhalb von liegen, haben somit den gleichen Abstand zur -Achse wie 
während der Abstand aller anderen Punkte innerhalb der Werbefläche zur -Achse größer ist.
-Achse entspricht der Symmetrieachse des Masts und stellt somit dessen Mittelgerade dar.
Da die Punkte und den gleichen Abstand zum Punkt auf der -Achse haben, ist der Abstand des Mittelpunkts der Strecke zur -Achse aus Symmetriegründen am kleinsten. Es hat also kein anderer Punkt auf der Strecke einen kleineren Abstand zur -Achse.
Aufgrund des vertikalen Verlaufs der Seitenkanten und gilt dies für alle weiteren Punkte innerhalb des Vierecks
Diejenigen Punkte, die vertikal unterhalb von liegen, haben somit den gleichen Abstand zur -Achse wie während der Abstand aller anderen Punkte innerhalb der Werbefläche zur -Achse größer ist.
d)
Winkel berechnen
Vektor der Sichtlinie bestimmen:
![\(\begin{array}[t]{rll}
\overrightarrow{GK}&=& \pmatrix{24\\15\\1}-\pmatrix{4\\-1\\11}& \\[5pt]
&=& \pmatrix{20\\16\\-10}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8357dc3ed1504d681e016eae9d85deb06643454009239948f3d4d455b53b592c_light.svg)
Ein Normalenvektor der Horizontalen ist beispielsweise 
Der Winkel der Sichtlinie gegenüber der Horizontalen ergibt sich nun durch:
Die Größe des Winkels der Sichtlinie gegenüber der Horizontalen beträgt somit ca. 
Ein Normalenvektor der Horizontalen ist beispielsweise
Der Winkel der Sichtlinie gegenüber der Horizontalen ergibt sich nun durch:
Die Größe des Winkels der Sichtlinie gegenüber der Horizontalen beträgt somit ca. 
![\(\begin{array}[t]{rll}
\sin (\alpha)&=& \dfrac{\left|\overrightarrow{GK} \circ \overrightarrow{n}\right|}{\left| \overrightarrow{GK} \right|\cdot \left| \overrightarrow{n} \right|} &\\[5pt]
\sin (\alpha)&=& \dfrac{\left| \pmatrix{20\\16\\-10} \circ \pmatrix{0\\0\\1} \right|}{ \left| \pmatrix{20\\16\\-10} \right|\cdot \left| \pmatrix{0\\0\\1} \right|}& \\[5pt]
\sin (\alpha)&=&\dfrac{10}{\sqrt{20^2+16^2+(-10)^2}\cdot 1} &\\[5pt]
\sin (\alpha)&\approx& 0,364 &\quad \scriptsize \mid \sin^{-1} \\[5pt]
\alpha&\approx& 21,35^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/ca9f1339b5d59b3a143b09c52ebea4966475ac736c7d6d54f7a76507bdd0eabd_light.svg)
e)
ist der Schnittpunkt der Gerade 
mit der Ebene, die die Punkte 
und 
enthält.
Eine Geradengleichung der Gerade 
ist beispielsweise gegeben durch:
![\(\begin{array}[t]{rll}
g_{BE}: \overrightarrow{x}&=& \overrightarrow{O B}+ s \cdot \overrightarrow{B E} & \\[5pt]
&=& \pmatrix{-2\\5\\11} +s\cdot \pmatrix{0\\0\\4}
\end{array}\)](https://www.schullv.de/resources/formulas/af4e3288cb8baabf09adef4cb60d1fae650c00ec13608a39057ea39a5360303f_light.svg)
Eine Ebenengleichung der Ebene 
folgt mit:
Gleichsetzen der beiden Gleichungen liefert folgendes Gleichungssystem:
![\(\begin{array}[t]{rll}
E_{KPQ}: \overrightarrow{x}&=& \overrightarrow{OK}+ t \cdot \overrightarrow{KP}+ u \cdot \overrightarrow{KQ}& \\[5pt]
&=& \pmatrix{24\\15\\1} +t\cdot \pmatrix{-4\\-20\\2} +u\cdot \pmatrix{-4\\10\\2}
\end{array}\)](https://www.schullv.de/resources/formulas/9685297ac862420ccbc9f97bc415ca00a3bfdf72f33f12fc544c63e2cf517a05_light.svg)
Das CAS liefert nun 
Einsetzen in 
ergibt:
![\(\begin{array}[t]{rll}
\overrightarrow{OH}&=& \pmatrix{-2\\5\\11} +\dfrac{3}{4} \cdot \pmatrix{0\\0\\4} \\[5pt]
&=& \pmatrix{-2\\5\\14}
\end{array}\)](https://www.schullv.de/resources/formulas/503360188f95f7e535330d3e4303621d333c4f044cf824f7f644a76fafbfcfc9_light.svg)
Die Koordinaten von folgen also mit 
f)
Jeder Punkt der Mauer hat die 
-Koordinate 20. Die Gleichung 
liefert eine Lösung 
.
Die Mauer hat eine Höhe von 
. Wenn 
gilt, trifft der Ball die Mauer, bevor er den Boden berührt.
-Koordinate 20. Die Gleichung liefert eine Lösung .
Die Mauer hat eine Höhe von . Wenn gilt, trifft der Ball die Mauer, bevor er den Boden berührt.