Aufgabe 2A
Betrachtet wird ein Glücksrad mit zwei Sektoren.

a) Beim Drehen dieses Glücksrads wird der Sektor „Stern“ mit einer Wahrscheinlichkeit von 40 % angezeigt.
Die Zufallsgröße  beschreibt die Anzahl der Ergebnisse „Stern“, wenn das Rad dreimal gedreht wird.
beschreibt die Anzahl der Ergebnisse „Stern“, wenn das Rad dreimal gedreht wird.
Geben Sie die Wahrscheinlichkeitsverteilung von an.
an.
Bestimmen Sie die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt.
Die Zufallsgröße beschreibt die Anzahl der Ergebnisse „Stern“, wenn das Rad 90-mal gedreht wird.
beschreibt die Anzahl der Ergebnisse „Stern“, wenn das Rad 90-mal gedreht wird.
Bestimmen Sie den Erwartungswert von .
.
Erläutern Sie, wie man ohne weitere Berechnungen die Wahrscheinlichkeiten für ,
,  und
und  bei 90 Drehungen vergleichen kann.
bei 90 Drehungen vergleichen kann.
Geben Sie die Wahrscheinlichkeitsverteilung von
Bestimmen Sie die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt.
Die Zufallsgröße
Bestimmen Sie den Erwartungswert von
Erläutern Sie, wie man ohne weitere Berechnungen die Wahrscheinlichkeiten für
(12P)
b) Ein Glücksrad steuert die Bewegung einer Spielfigur auf dem unten abgebildeten Spielfeld nach folgenden Regeln:
Für dieses Glücksrad gibt  den Anteil des Sektors „Stern“ an.
Erläutern Sie, dass die Wahrscheinlichkeit für das Erreichen eines der beiden Zielfelder durch den Term
den Anteil des Sektors „Stern“ an.
Erläutern Sie, dass die Wahrscheinlichkeit für das Erreichen eines der beiden Zielfelder durch den Term  berechnet werden kann.
Die Wahrscheinlichkeit für das Erreichen eines der beiden Zielfelder soll mindestens 15 % betragen.
Ermitteln Sie die möglichen Werte für
berechnet werden kann.
Die Wahrscheinlichkeit für das Erreichen eines der beiden Zielfelder soll mindestens 15 % betragen.
Ermitteln Sie die möglichen Werte für  . (Genauigkeit der Angaben: zwei Nachkommastellen)
. (Genauigkeit der Angaben: zwei Nachkommastellen)
- Zeigt das Rad „Stern“, so wird die Figur um ein Feld nach rechts gerückt.
- Zeigt das Rad nicht „Stern“, so wird die Figur um ein Feld nach links gerückt.
- Ist eines der beiden Zielfelder erreicht, so ist das Spiel beendet.
- Das Glücksrad wird bei einem Spiel höchstens sechsmal gedreht.
| Ziel | Start | Ziel |
(12P)
(24P)
a)  Wahrscheinlichkeitsverteilung von
Wahrscheinlichkeitsverteilung von  angeben
Deine Aufgabe ist es, die Wahrscheinlichkeitsverteilung der Zufallsvariablen
angeben
Deine Aufgabe ist es, die Wahrscheinlichkeitsverteilung der Zufallsvariablen  anzugeben. Der Aufgabenstellung kannst du dabei entnehmen, dass
anzugeben. Der Aufgabenstellung kannst du dabei entnehmen, dass  die Anzahl der Ergebnisse „ Stern “, beschreibt, wenn das Glücksrad dreimal gedreht wird.
die Anzahl der Ergebnisse „ Stern “, beschreibt, wenn das Glücksrad dreimal gedreht wird.
Überlege dir nun, welche Arten der Wahrscheinlichkeitsverteilungen du kennst. Wähle anschließend die passende aus und gib die entsprechenden Parameter an. Gib anschließend die Wahrscheinlichkeiten der einzelnen Wahrscheinlichkeiten an, also ,
,  ,
,  und
und  .
Du kennst beispielsweise die Binomialverteilung. Diese kommt häufig im Zusammenhang mit der Anzahl des Auftretens eines bestimmten Ereignisses vor.
.
Du kennst beispielsweise die Binomialverteilung. Diese kommt häufig im Zusammenhang mit der Anzahl des Auftretens eines bestimmten Ereignisses vor.
Damit eine Zufallsvariable als binomialverteilt angenommen werden kann, müssen zwei Bedingungen erfüllt sein: diese Bedingungen erfüllt. Ist dies der Fall, so ist
diese Bedingungen erfüllt. Ist dies der Fall, so ist  binomialverteilt.
zwei Ausprägungen
In diesem Fall beschreibt
binomialverteilt.
zwei Ausprägungen
In diesem Fall beschreibt  , wie oft das Ergebnis „Stern“, in drei Runden auftritt. Das heißt, dass hier nur die beiden Ausprägungen „Stern“, und „nicht Stern“, betrachtet werden. Diese Bedingung ist also erfüllt.
gleiche Wahrscheinlichkeit
Bei jedem Dreh bleibt die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird gleich groß. Daher ist auch diese Bedingung erfüllt.
, wie oft das Ergebnis „Stern“, in drei Runden auftritt. Das heißt, dass hier nur die beiden Ausprägungen „Stern“, und „nicht Stern“, betrachtet werden. Diese Bedingung ist also erfüllt.
gleiche Wahrscheinlichkeit
Bei jedem Dreh bleibt die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird gleich groß. Daher ist auch diese Bedingung erfüllt.
Die Zufallsvariable ist also binomialverteilt.
ist also binomialverteilt.
Eine Zufallsvariable ist immer mit zwei Parametern binomialverteilt: , weil dreimal gedreht wird, und
, weil dreimal gedreht wird, und  , da die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird
, da die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird  beträgt.
Berechne nun noch die elemantaren Wahrscheinlichkeiten. Dies kannst du mit Hilfe der Formel für die Binomialverteilung oder mit deinem GTR tun. Die entsprechende Formel lautet:
beträgt.
Berechne nun noch die elemantaren Wahrscheinlichkeiten. Dies kannst du mit Hilfe der Formel für die Binomialverteilung oder mit deinem GTR tun. Die entsprechende Formel lautet:

 Lösungsweg A: Formel für die Binomialverteilung
Setzt du hier
Lösungsweg A: Formel für die Binomialverteilung
Setzt du hier  und
und  , sowie nacheinander
, sowie nacheinander  ,
,  ,
,  und
und  ein, so erhältst du:
ein, so erhältst du:




 Lösungsweg B: CAS
Hierzu kannst du den binomPdf-Befehl deines CAS verwenden. Diesen findest du unter
menu:
Lösungsweg B: CAS
Hierzu kannst du den binomPdf-Befehl deines CAS verwenden. Diesen findest du unter
menu:  5:
5:  5:
5:  D:
Dort musst du die entsprechenden Parameter eingeben.
D:
Dort musst du die entsprechenden Parameter eingeben.
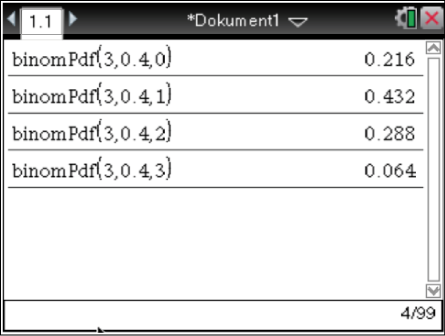 Du erhältst dann:
Du erhältst dann:
 ,
,  ,
,  und
und  Die Zufallsvariable
Die Zufallsvariable  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und  . Dabei gilt:
. Dabei gilt:
 ,
,  ,
,  und
und 
 Mindestanzahl der Drehungen
Bestimme die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt. Es soll also gelten:
Mindestanzahl der Drehungen
Bestimme die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt. Es soll also gelten:
 Es müssen mindestens 10 Drehungen erfolgen.
Es müssen mindestens 10 Drehungen erfolgen.
 Erwartungswert von
Erwartungswert von  bestimmen
Hier sollst du nun den Erwartungswert einer neuen Zufallsvariablen
bestimmen
Hier sollst du nun den Erwartungswert einer neuen Zufallsvariablen  bestimmen. Der Aufgabenstellung kannst du dabei entnehmen, dass
bestimmen. Der Aufgabenstellung kannst du dabei entnehmen, dass  die Anzahl der Ergebnisse „Stern“, beschreibt, wenn 90-mal gedreht wird. Aus den gleichen Gründen wie oben, kann auch
die Anzahl der Ergebnisse „Stern“, beschreibt, wenn 90-mal gedreht wird. Aus den gleichen Gründen wie oben, kann auch  als binomialverteilt angenommen werden mit den Parametern
als binomialverteilt angenommen werden mit den Parametern  und
und  .
.
Den Erwartungswert einer binomialverteilten Zufallsvariablen kannst du mit Hilfe folgender Formel berechnen:
einer binomialverteilten Zufallsvariablen kannst du mit Hilfe folgender Formel berechnen:
 Da du
Da du  und
und  kennst, kannst du hier einfach einsetzen:
kennst, kannst du hier einfach einsetzen:
 Der Erwartungswert der Zufallsvariablen
Der Erwartungswert der Zufallsvariablen  beträgt
beträgt  .
.
 Vergleich der drei Wahrscheinlichkeiten
Nun sollst du angeben, wie man die drei Wahrscheinlichkeiten für
Vergleich der drei Wahrscheinlichkeiten
Nun sollst du angeben, wie man die drei Wahrscheinlichkeiten für  ,
,  und
und  vergleichen kann ohne diese zu berechnen.
vergleichen kann ohne diese zu berechnen.
Da du bisher nur die Wahrscheinlichkeitsverteilung und den Erwartungswert von kennst, muss dieser Vergleich mit Hilfe dieser Informationen stattfinden. Dabei kann dir die folgende Information helfen:
Ist eine Zufallsvariable
kennst, muss dieser Vergleich mit Hilfe dieser Informationen stattfinden. Dabei kann dir die folgende Information helfen:
Ist eine Zufallsvariable  binomialverteilt mit dem Erwartungswert
binomialverteilt mit dem Erwartungswert  , so liegt das Maximum der Verteilung bei
, so liegt das Maximum der Verteilung bei  . Das heißt
. Das heißt  ist größer als alle anderen Wahrscheinlichkeiten
ist größer als alle anderen Wahrscheinlichkeiten  , wenn
, wenn  gilt.
gilt.
Je weiter andere Werte für von
von  abweichen, desto kleiner ist auch die Wahrscheinlichkeit
abweichen, desto kleiner ist auch die Wahrscheinlichkeit  .
Diese Information kannst du nun mit Hilfe von
.
Diese Information kannst du nun mit Hilfe von  auf die gegebene Problemstellung übertragen.
Da
auf die gegebene Problemstellung übertragen.
Da  binomialverteilt ist und für den Erwartungswert
binomialverteilt ist und für den Erwartungswert  gilt, ist
gilt, ist  das Maximum. Da
das Maximum. Da  stärker vom Erwartungswert
stärker vom Erwartungswert  abweicht, als
abweicht, als  muss
muss  kleiner sein als
kleiner sein als  . Damit gilt insgesamt:
. Damit gilt insgesamt:
 .
.
Überlege dir nun, welche Arten der Wahrscheinlichkeitsverteilungen du kennst. Wähle anschließend die passende aus und gib die entsprechenden Parameter an. Gib anschließend die Wahrscheinlichkeiten der einzelnen Wahrscheinlichkeiten an, also
Damit eine Zufallsvariable als binomialverteilt angenommen werden kann, müssen zwei Bedingungen erfüllt sein:
- Das betrachtete Merkmal darf nur zwei verschiedene Ausprägungen besitzen.
- Die Wahrscheinlichkeiten für diese Ausprägungen müssen in jedem Durchgang gleich bleiben (Ziehen mit Zurücklegen).
Die Zufallsvariable
Eine Zufallsvariable ist immer mit zwei Parametern binomialverteilt:
ist der Stichprobenumfang.
ist die Wahrscheinlichkeit des Merkmals das betrachtet wird.

Den Erwartungswert
Da du bisher nur die Wahrscheinlichkeitsverteilung und den Erwartungswert von
Je weiter andere Werte für
b)  Erläutern der Wahrscheinlichkeit
Du kannst die Wahrscheinlichkeit erläutern, indem du jeden Summanden einzeln betrachtest.
Um das linke Zielfeld zu erreichen muss 6 mal „nicht Stern“ auftreten:
Erläutern der Wahrscheinlichkeit
Du kannst die Wahrscheinlichkeit erläutern, indem du jeden Summanden einzeln betrachtest.
Um das linke Zielfeld zu erreichen muss 6 mal „nicht Stern“ auftreten:  Um das rechte Zielfeld zu erreichen gibt es zwei Möglichkeiten:
Um das rechte Zielfeld zu erreichen gibt es zwei Möglichkeiten:
 Ermittle mögliche Werte für p
Du sollst die Werte für
Ermittle mögliche Werte für p
Du sollst die Werte für  ermitteln, sodass in mindestens
ermitteln, sodass in mindestens  der Fälle das Ziel erreicht wird:
der Fälle das Ziel erreicht wird:
 Gib diese Funktion in deinen Taschenrechner ein, es interessieren dich nur die Bereiche Zwischen 0 und 1, da
Gib diese Funktion in deinen Taschenrechner ein, es interessieren dich nur die Bereiche Zwischen 0 und 1, da  eine Wahrscheinlichkeit ist.
eine Wahrscheinlichkeit ist.
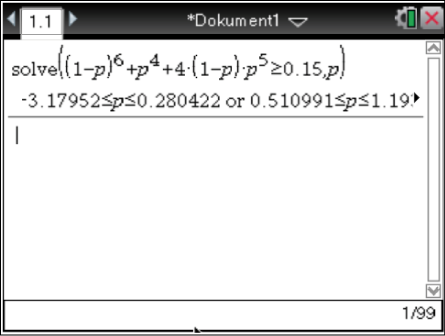 Die Bereiche, in denen die Wahrscheinlichkeit größer als 0,15 ist, sind dann gegeben durch
Die Bereiche, in denen die Wahrscheinlichkeit größer als 0,15 ist, sind dann gegeben durch ![\(\boldsymbol{[0;0,28]}\)](https://www.schullv.de/resources/formulas/d2509fcf3e2d76240687c57972d46a89e6c4d86b41266ef0af32eeec5ce6cb6c_light.svg) und
und ![\(\boldsymbol{[0,51;1]}\)](https://www.schullv.de/resources/formulas/7a04fe00f6d5d60182141596df4ef5f14036b426377f7ae210a5642e4fd0f385_light.svg) .
.
- 4 mal „Stern“:
- 1 mal „nicht Stern“ und 5 mal „Stern“:
(für diese Wahrscheinlichkeit gibt es 4 mögliche Reihenfolgen)

a)  Wahrscheinlichkeitsverteilung von
Wahrscheinlichkeitsverteilung von  angeben
Deine Aufgabe ist es, die Wahrscheinlichkeitsverteilung der Zufallsvariablen
angeben
Deine Aufgabe ist es, die Wahrscheinlichkeitsverteilung der Zufallsvariablen  anzugeben. Der Aufgabenstellung kannst du dabei entnehmen, dass
anzugeben. Der Aufgabenstellung kannst du dabei entnehmen, dass  die Anzahl der Ergebnisse „ Stern “, beschreibt, wenn das Glücksrad dreimal gedreht wird.
die Anzahl der Ergebnisse „ Stern “, beschreibt, wenn das Glücksrad dreimal gedreht wird.
Überlege dir nun, welche Arten der Wahrscheinlichkeitsverteilungen du kennst. Wähle anschließend die passende aus und gib die entsprechenden Parameter an. Gib anschließend die Wahrscheinlichkeiten der einzelnen Wahrscheinlichkeiten an, also ,
,  ,
,  und
und  .
Du kennst beispielsweise die Binomialverteilung. Diese kommt häufig im Zusammenhang mit der Anzahl des Auftretens eines bestimmten Ereignisses vor.
.
Du kennst beispielsweise die Binomialverteilung. Diese kommt häufig im Zusammenhang mit der Anzahl des Auftretens eines bestimmten Ereignisses vor.
Damit eine Zufallsvariable als binomialverteilt angenommen werden kann, müssen zwei Bedingungen erfüllt sein: diese Bedingungen erfüllt. Ist dies der Fall, so ist
diese Bedingungen erfüllt. Ist dies der Fall, so ist  binomialverteilt.
zwei Ausprägungen
In diesem Fall beschreibt
binomialverteilt.
zwei Ausprägungen
In diesem Fall beschreibt  , wie oft das Ergebnis „Stern“, in drei Runden auftritt. Das heißt, dass hier nur die beiden Ausprägungen „Stern“, und „nicht Stern“, betrachtet werden. Diese Bedingung ist also erfüllt.
gleiche Wahrscheinlichkeit
Bei jedem Dreh bleibt die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird gleich groß. Daher ist auch diese Bedingung erfüllt.
, wie oft das Ergebnis „Stern“, in drei Runden auftritt. Das heißt, dass hier nur die beiden Ausprägungen „Stern“, und „nicht Stern“, betrachtet werden. Diese Bedingung ist also erfüllt.
gleiche Wahrscheinlichkeit
Bei jedem Dreh bleibt die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird gleich groß. Daher ist auch diese Bedingung erfüllt.
Die Zufallsvariable ist also binomialverteilt.
ist also binomialverteilt.
Eine Zufallsvariable ist immer mit zwei Parametern binomialverteilt: , weil dreimal gedreht wird, und
, weil dreimal gedreht wird, und  , da die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird
, da die Wahrscheinlichkeit dafür, dass „Stern“, gedreht wird  beträgt.
Berechne nun noch die elemantaren Wahrscheinlichkeiten. Dies kannst du mit Hilfe der Formel für die Binomialverteilung oder mit deinem GTR tun. Die entsprechende Formel lautet:
beträgt.
Berechne nun noch die elemantaren Wahrscheinlichkeiten. Dies kannst du mit Hilfe der Formel für die Binomialverteilung oder mit deinem GTR tun. Die entsprechende Formel lautet:

 Lösungsweg A: Formel für die Binomialverteilung
Setzt du hier
Lösungsweg A: Formel für die Binomialverteilung
Setzt du hier  und
und  , sowie nacheinander
, sowie nacheinander  ,
,  ,
,  und
und  ein, so erhältst du:
ein, so erhältst du:




 Lösungsweg B: CAS
Hierzu kannst du den Binompdf-Befehl deines CAS verwenden. Diesen findest du im Statistik-Menü unter
CALC
Lösungsweg B: CAS
Hierzu kannst du den Binompdf-Befehl deines CAS verwenden. Diesen findest du im Statistik-Menü unter
CALC  Verteilung
Verteilung  Binom. Einzelwkt.
Bestätigst du mit Weiter, so musst du die entsprechenden Parameter eingeben. In ersten Bilders ist dies beispielhaft für
Binom. Einzelwkt.
Bestätigst du mit Weiter, so musst du die entsprechenden Parameter eingeben. In ersten Bilders ist dies beispielhaft für  dargestellt:
dargestellt:
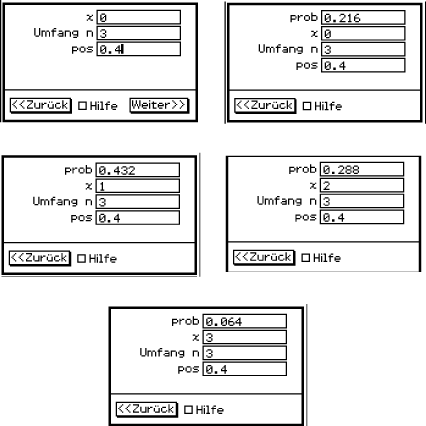 Du erhältst dann:
Du erhältst dann:
 ,
,  ,
,  und
und  Die Zufallsvariable
Die Zufallsvariable  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und  . Dabei gilt:
. Dabei gilt:
 ,
,  ,
,  und
und 
 Mindestanzahl der Drehungen
Bestimme die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt. Es soll also gelten:
Mindestanzahl der Drehungen
Bestimme die Mindestanzahl der Drehungen so, dass mit einer Wahrscheinlichkeit von mehr als 99 % mindestens einmal das Ergebnis „Stern“ auftritt. Es soll also gelten:
 Es müssen mindestens 10 Drehungen erfolgen.
Es müssen mindestens 10 Drehungen erfolgen.
 Erwartungswert von
Erwartungswert von  bestimmen
Hier sollst du nun den Erwartungswert einer neuen Zufallsvariablen
bestimmen
Hier sollst du nun den Erwartungswert einer neuen Zufallsvariablen  bestimmen. Der Aufgabenstellung kannst du dabei entnehmen, dass
bestimmen. Der Aufgabenstellung kannst du dabei entnehmen, dass  die Anzahl der Ergebnisse „Stern“, beschreibt, wenn 90-mal gedreht wird. Aus den gleichen Gründen wie oben, kann auch
die Anzahl der Ergebnisse „Stern“, beschreibt, wenn 90-mal gedreht wird. Aus den gleichen Gründen wie oben, kann auch  als binomialverteilt angenommen werden mit den Parametern
als binomialverteilt angenommen werden mit den Parametern  und
und  .
.
Den Erwartungswert einer binomialverteilten Zufallsvariablen kannst du mit Hilfe folgender Formel berechnen:
einer binomialverteilten Zufallsvariablen kannst du mit Hilfe folgender Formel berechnen:
 Da du
Da du  und
und  kennst, kannst du hier einfach einsetzen:
kennst, kannst du hier einfach einsetzen:
 Der Erwartungswert der Zufallsvariablen
Der Erwartungswert der Zufallsvariablen  beträgt
beträgt  .
.
 Vergleich der drei Wahrscheinlichkeiten
Nun sollst du angeben, wie man die drei Wahrscheinlichkeiten für
Vergleich der drei Wahrscheinlichkeiten
Nun sollst du angeben, wie man die drei Wahrscheinlichkeiten für  ,
,  und
und  vergleichen kann ohne diese zu berechnen.
vergleichen kann ohne diese zu berechnen.
Da du bisher nur die Wahrscheinlichkeitsverteilung und den Erwartungswert von kennst, muss dieser Vergleich mit Hilfe dieser Informationen stattfinden. Dabei kann dir die folgende Information helfen:
Ist eine Zufallsvariable
kennst, muss dieser Vergleich mit Hilfe dieser Informationen stattfinden. Dabei kann dir die folgende Information helfen:
Ist eine Zufallsvariable  binomialverteilt mit dem Erwartungswert
binomialverteilt mit dem Erwartungswert  , so liegt das Maximum der Verteilung bei
, so liegt das Maximum der Verteilung bei  . Das heißt
. Das heißt  ist größer als alle anderen Wahrscheinlichkeiten
ist größer als alle anderen Wahrscheinlichkeiten  , wenn
, wenn  gilt.
gilt.
Je weiter andere Werte für von
von  abweichen, desto kleiner ist auch die Wahrscheinlichkeit
abweichen, desto kleiner ist auch die Wahrscheinlichkeit  .
Diese Information kannst du nun mit Hilfe von
.
Diese Information kannst du nun mit Hilfe von  auf die gegebene Problemstellung übertragen.
Da
auf die gegebene Problemstellung übertragen.
Da  binomialverteilt ist und für den Erwartungswert
binomialverteilt ist und für den Erwartungswert  gilt, ist
gilt, ist  das Maximum. Da
das Maximum. Da  stärker vom Erwartungswert
stärker vom Erwartungswert  abweicht, als
abweicht, als  muss
muss  kleiner sein als
kleiner sein als  . Damit gilt insgesamt:
. Damit gilt insgesamt:
 .
.
Überlege dir nun, welche Arten der Wahrscheinlichkeitsverteilungen du kennst. Wähle anschließend die passende aus und gib die entsprechenden Parameter an. Gib anschließend die Wahrscheinlichkeiten der einzelnen Wahrscheinlichkeiten an, also
Damit eine Zufallsvariable als binomialverteilt angenommen werden kann, müssen zwei Bedingungen erfüllt sein:
- Das betrachtete Merkmal darf nur zwei verschiedene Ausprägungen besitzen.
- Die Wahrscheinlichkeiten für diese Ausprägungen müssen in jedem Durchgang gleich bleiben (Ziehen mit Zurücklegen).
Die Zufallsvariable
Eine Zufallsvariable ist immer mit zwei Parametern binomialverteilt:
ist der Stichprobenumfang.
ist die Wahrscheinlichkeit des Merkmals das betrachtet wird.

Den Erwartungswert
Da du bisher nur die Wahrscheinlichkeitsverteilung und den Erwartungswert von
Je weiter andere Werte für
b)  Erläutern der Wahrscheinlichkeit
Du kannst die Wahrscheinlichkeit erläutern, indem du jeden Summanden einzeln betrachtest.
Um das linke Zielfeld zu erreichen muss 6 mal „nicht Stern“ auftreten:
Erläutern der Wahrscheinlichkeit
Du kannst die Wahrscheinlichkeit erläutern, indem du jeden Summanden einzeln betrachtest.
Um das linke Zielfeld zu erreichen muss 6 mal „nicht Stern“ auftreten:  Um das rechte Zielfeld zu erreichen gibt es zwei Möglichkeiten:
Um das rechte Zielfeld zu erreichen gibt es zwei Möglichkeiten:
 Ermittle mögliche Werte für p
Du sollst die Werte für
Ermittle mögliche Werte für p
Du sollst die Werte für  ermitteln, sodass in mindestens
ermitteln, sodass in mindestens  der Fälle das Ziel erreicht wird:
der Fälle das Ziel erreicht wird:
 Gib diese Funktion in deinen Taschenrechner ein, es interessieren dich nur die Bereiche Zwischen 0 und 1, da
Gib diese Funktion in deinen Taschenrechner ein, es interessieren dich nur die Bereiche Zwischen 0 und 1, da  eine Wahrscheinlichkeit ist.
eine Wahrscheinlichkeit ist.
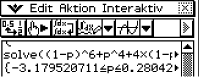 Die Bereiche, in denen die Wahrscheinlichkeit größer als 0,15 ist, sind dann gegeben durch
Die Bereiche, in denen die Wahrscheinlichkeit größer als 0,15 ist, sind dann gegeben durch ![\(\boldsymbol{[0;0,28]}\)](https://www.schullv.de/resources/formulas/d2509fcf3e2d76240687c57972d46a89e6c4d86b41266ef0af32eeec5ce6cb6c_light.svg) und
und ![\(\boldsymbol{[0,51;1]}\)](https://www.schullv.de/resources/formulas/7a04fe00f6d5d60182141596df4ef5f14036b426377f7ae210a5642e4fd0f385_light.svg) .
.
- 4 mal „Stern“:
- 1 mal „nicht Stern“ und 5 mal „Stern“:
(für diese Wahrscheinlichkeit gibt es 4 mögliche Reihenfolgen)
