Aufgabe 2A

Das Spiel „Die goldene Zehn“ wird mit einem idealen Würfel gespielt, bei dem eine Seitenfläche mit einem „V“, zwei Seitenflächen mit einer „ $2$ “, zwei mit einer „ $5$ “ und eine mit einer „ $10$ “ bedruckt sind.

Es gelten folgende Spielregeln:

Zu Beginn eines Spiels beträgt die Punktzahl des Spielers null.
Zeigt der Würfel nach einem Wurf eine Zahl, wird diese zur bisherigen Punktzahl addiert.
Der Spieler gewinnt, wenn er genau die Punktzahl $10$ erreicht.
Er verliert, wenn er eine Punktzahl größer als $10$ erreicht oder ein „V“ würfelt.
Das Spiel ist beendet, wenn der Spieler gewonnen oder verloren hat.

Der Spieler zahlt vor dem Spiel einen Einsatz von einem Euro an den Spielleiter. Gewinnt der Spieler, so bekommt er pro Wurf in diesem Spiel zwei Euro ausgezahlt.

Das Spiel wird einmal gespielt. Bestimme die Wahrscheinlichkeit dafür, dass der Spieler mit zwei Würfen die Punktzahl $12$ erreicht.

(3P)

Die Zufallsgröße $X$ beschreibt den an den Spieler ausgezahlten Betrag in Euro.

Für die Wahrscheinlichkeitsverteilung von $X$ gilt:

$k$	$0$	$2$	$4$	$10$
$P(X=k)$	$\dfrac{349}{486}$	$\dfrac{1}{6}$	$\dfrac{1}{9}$	$\dfrac{1}{243}$

Begründe, dass $X$ nur die Werte $0$ , $2$ , $4$ oder $10$ annehmen kann.

Begründe, dass das Spiel nicht fair ist.

Untersuche, ob bei unverändertem Einsatz von einem Euro der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair wird.

(9P)

Bestimme die Wahrscheinlichkeit dafür, dass der Spieler von $120$ Spielen mindestens $30$ und höchstens $50$ gewinnt.

Erläutere, welche Wahrscheinlichkeit im Sachzusammenhang des Spiels ‚Die goldene Zehn‘ mit dem Term $1-19\cdot\dfrac{349}{486}\cdot\left(\dfrac{137}{486}\right)^{18}$ berechnet werden kann.

(8P)

Unabhängig vom Sachzusammenhang ist über eine Urne Folgendes bekannt:

In der Urne befinden sich neben anderen Kugeln genau fünf gelbe Kugeln.
Es werden zwei Kugeln gleichzeitig aus der Urne gezogen.
Die Wahrscheinlichkeit, genau eine gelbe Kugel zu erhalten, beträgt $\dfrac{1}{3}$ .

Leite eine Gleichung zur Bestimmung der Anzahl aller Kugeln in der Urne her.

(4P)

Aufgabe 2A

$\blacktriangleright$ Wahrscheinlichkeit berechnen

In dieser Aufgabe sollst du die Wahrscheinlichkeit $P(X=12)$ dafür berechnen, dass der Spieler mit zwei Würfen die Punktzahl $12$ erreicht. Ein Spieler kann hierbei nur die Punktzahl $12$ erreichen, wenn er eine $2$ und anschließend eine $10$ würfelt. Falls der Spieler zuerst eine $10$ würfelt, hätte der Spieler gewonnen und das Spiel wäre beendet.

Die einzige Möglichkeit ist somit, dass der Spieler zuerst eine $2$ würfelt und anschließend eine $10$ . Die Wahrscheinlichkeit, eine $2$ zu würfeln, liegt hierbei bei $P(X=2)=\dfrac{2}{6}$ und eine $10$ zu würfeln bei $P(X=10)=\dfrac{1}{6}$ . Somit ergibt sich mit der Pfadregel folgende Wahrscheinlichkeit:

$P(X=12)=\dfrac{1}{18}$

Vollständige Lösung anzeigen

Somit beträgt die Wahrscheinlichkeit dafür, dass ein Spieler mit zwei Würfen die Punktzahl $12$ erreicht, $P(X=12)=\dfrac{1}{18}$ .

$\blacktriangleright$ $\boldsymbol{X}$ -Werte begründen

In dieser Teilaufgabe sollst du begründen, dass $X$ nur die Werte $0$ , $2$ , $4$ oder $10$ annehmen kann. $X$ gibt hierbei den an den Spieler ausgezahlten Betrag in Euro an.

Der Spieler kann in einem Spiel verlieren oder gewinnen. Verliert der Spieler, bekommt er $0$ Euro ausgezahlt. Gewinnt der Spieler, bekommt er pro Wurf in diesem Spiel $2$ Euro ausgezahlt. Hierbei ist zu beachten, dass ein Spieler nur dann gewinnt, wenn er genau die Punktzahl $10$ erreicht. Es ist also zu überlegen, welche Möglichkeiten es gibt, genau die Punktzahl $10$ zu erreichen.

Eine Möglichkeit besteht darin, dass der Spieler beim ersten Wurf die Punktzahl $10$ würfelt. Somit würde der Spieler einen Betrag von $2$ Euro ausgezahlt bekommen, da er nur einmal gewürfelt hat.

Eine weitere Möglichkeit ist, dass der Spieler zweimal die Punktzahl $5$ würfelt. Somit würde der Spieler $4$ Euro ausgezahlt bekommen, da er zweimal gewürfelt hat.

Die letzte Möglichkeit ist, dass der Spieler fünfmal die Punktzahl $2$ würfelt. Dadurch würde der Auszahlungsbetrag auf $10$ Euro ansteigen.

Dies sind alle Möglichkeiten, die für den Auszahlungsbetrag auftreten können. Deshalb kann $X$ nur die Werte $0$ , $2$ , $4$ oder $10$ annehmen.

$\blacktriangleright$ Begründen, dass das Spiel nicht fair ist

In dieser Teilaufgabe sollst du begründen, dass das Spiel nicht fair ist. Dazu muss der Erwartungswert berechnet werden. Der Erwartungswert lässt sich mit folgender Formel berechnen:

E(X) = ∑_i=1ⁿ k_i · P(X=k_i) = k₁·P(X=k₁) + k₂·P(X=k₂) + … + kₙ·P(X=kₙ)

$X$ bezeichnet hierbei den ausgezahlten Betrag in Euro. Zuerst wird der Erwartungswert für den ausgezahlten Betrag berechnet. Um zu begründen, dass das Spiel nicht fair ist, wird anschließend noch der Einsatz von $1$ Euro abgezogen. Damit das Spiel fair ist, muss $E(X)=0$ gelten.

Für den Erwartungswert des Spiels folgt mit der angegebenen Wahrscheinlichkeitsverteilung und dem Einsatz $S=1\,\text{€}$ :

$E(X)=-\dfrac{44}{243}\,\text{€}$

Vollständige Lösung anzeigen

Somit beträgt der Erwartungswert $E(X)=- \dfrac{44}{243}\,\text{€}$ und dies ist ungleich Null. Deshalb ist das Spiel nicht fair.

$\blacktriangleright$ Auszahlungsbetrag verändern

In dieser Teilaufgabe sollst du untersuchen, ob bei einem unveränderten Einsatz von $1\,\text{€}$ der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair ist. Bezeichne hierbei den Auszahlungsbetrag pro Wurf mit $Y$ . Nun wird der Auszahlungsbetrag pro Wurf so abgeändert, dass $E(X)=0$ gilt. Stelle dazu den Erwartungswert in Abhängigkeit des Auszahlungsbetrags dar und löse nach $Y$ auf.

$Y=\dfrac{486}{199}\,\text{€}$

Vollständige Lösung anzeigen

Somit gilt: Für einen Auszahlungsbetrag von $\dfrac{486}{199}\,\text{€}$ ist das Spiel fair.

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür bestimmen, dass der Spieler von $120$ Spielen mindestens $30$ und höchstens $50$ gewinnt. Somit ist die gesuchte Wahrscheinlichkeit $P(30 \leq X \leq 50)$ . Die Wahrscheinlichkeit, dass ein Spieler verliert, liegt bei $P(X=0)=\dfrac{349}{486}$ . Entsprechend gilt für die Gewinnwahrscheinlichkeit $p$ (Gegenereignis):

$\begin{array}[t]{rll} p &=& 1 - P(X=0)\\[5pt] &=& 1 - \dfrac{349}{486}\\[5pt] &=& \dfrac{137}{486} \end{array}$

Die gesuchte Wahrscheinlichkeit kann mit der Binomialverteilung berechnet werden. Man kann schreiben:

$P(30 \leq X \leq 50)=P(X\leq 50)-P(X\leq 29)$

Vollständige Lösung anzeigen

Zudem ist gegeben, dass der Spieler insgesamt $n=120$ Spiele spielt. Verwende den binomcdf-Befehl deines CAS. Diesen findest du unter

5: Wahrscheinlichkeiten → 5: Verteilungen → E: Binomial Cdf.

Für die Wahrscheinlichkeiten folgt mit deinem CAS:

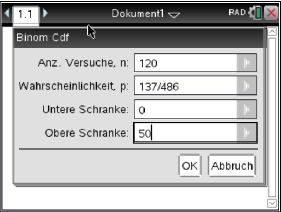Screenshot eines Fensters mit Eingabefeldern für eine binomiale Verteilung.

Abb. 1: Eingetragene Daten

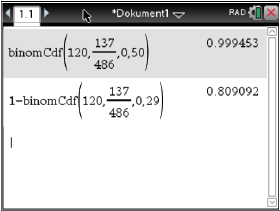Mathematik-Dokument mit Berechnungen zur Binomialverteilung.

Abb. 2: Ergebnis

Somit beträgt die Wahrscheinlichkeit, dass der Spieler von $120$ Spielen mindestens $30$ und höchstens $50$ gewinnt, $P(30 \leq X \leq 50)\approx 0{,}809$ .

$\blacktriangleright$ Wahrscheinlichkeit erläutern

In dieser Teilaufgabe sollst du erläutern, welche Wahrscheinlichkeit mit dem Term $1- 19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ berechnet werden kann. Der Term $19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ gibt hierbei die Wahrscheinlichkeit dafür an, dass ein Spieler von $19$ Spielen einmal verliert und $18$ -mal gewinnt. Dies lässt sich auch durch die folgende Formel zur Berechnung der Wahrscheinlichkeit bei einer Binomialverteilung verdeutlichen:

$P(X=k)=\binom{n}{k}\cdot p^k\cdot (1-p)^{n-k}$

In diesem Fall gilt $k=1$ , $n=19$ und $p=\dfrac{349}{486}$ .

Der gesamte Term $1- 19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ bezeichnet das Gegenereignis des Terms $19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ . Somit berechnet der gegebene Term die Wahrscheinlichkeit dafür, dass ein Spieler von $19$ Spielen nicht genau einmal verliert und nicht $18$ -mal gewinnt.

$\blacktriangleright$ Gleichung herleiten

In dieser Aufgabe sollst du eine Gleichung zur Bestimmung der Anzahl aller Kugeln in einer Urne herleiten. Hierfür ist gegeben, dass sich neben anderen Kugeln genau fünf gelbe Kugeln befinden. Außerdem ist bekannt, dass wenn zwei Kugeln gleichzeitig aus der Urne gezogen werden, die Wahrscheinlichkeit, eine gelbe zu bekommen, $\dfrac{1}{3}$ beträgt. Zur Hilfe kann ein zweistufiges Baumdiagramm mit den Pfaden „gelb“ oder „nicht gelb“ gezeichnet werden.

Bezeichne die Gesamtanzahl aller Kugeln in der Urne mit $n$ . Somit folgt für die Anzahl aller nicht gelben Kugeln $n-5$ , da in der Urne genau $5$ gelbe Kugeln sind. Es handelt sich um Ziehen ohne Zurücklegen, d. h. beim zweiten Ziehen befinden sich nur noch $n-1$ Kugeln in der Urne.

Das Baumdiagramm mit den einzelnen Wahrscheinlichkeiten ergibt sich dann wie folgt:

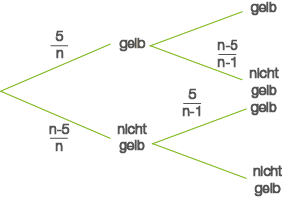Baumdiagramm mit Wahrscheinlichkeiten für die Farben gelb und nicht gelb.

Abb. 3: Baumdiagramm

Gegeben ist die Wahrscheinlichkeit dafür, dass genau eine der beiden gezogenen Kugeln gelb ist. Dafür gibt es zwei Möglichkeiten: zuerst „nicht gelb“, dann „gelb“ oder zuerst „gelb“, dann „nicht gelb“.

Für die Wahrscheinlichkeit $P$ , dass beim Ziehen von zwei Kugeln genau eine gelb ist, folgt:

Da $P=\dfrac{1}{3}$ gilt, folgt die Gleichung $\frac{1}{3}=2\cdot \frac{5}{n}\cdot\frac{n-5}{n-1}$ zur Bestimmung der Gesamtanzahl $n$ der Kugeln in der Urne.

Bildnachweise [nach oben]

[1]

[2]

[3]

Aufgabe 2A

$\blacktriangleright$ Wahrscheinlichkeit berechnen

In dieser Aufgabe sollst du die Wahrscheinlichkeit $P(X=12)$ dafür berechnen, dass der Spieler mit zwei Würfen die Punktzahl $12$ erreicht. Ein Spieler kann hierbei nur die Punktzahl $12$ erreichen, wenn er eine $2$ und anschließend eine $10$ würfelt. Falls der Spieler zuerst eine $10$ würfelt hätte der Spieler gewonnen und das Spiel wäre beendet.

Die einzige Möglichkeit ist somit, dass der Spieler zuerst eine $2$ würfelt und anschließend eine $10$ . Die Wahrscheinlichkeit eine $2$ zu würfeln liegt hierbei bei $P(X=2)=\dfrac{2}{6}$ und eine $10$ zu würfeln bei $P(X=10)=\dfrac{1}{6}$ . Somit ergibt sich mit der Pfadregel folgende Wahrscheinlichkeit:

$P(X=12) =\dfrac{1}{18}$

Vollständige Lösung anzeigen

Somit beträgt die Wahrscheinlichkeit dafür, dass ein Spieler mit zwei Würfen die Punktzahl $12$ erreicht $P(X=12)=\dfrac{1}{18}$ .

$\blacktriangleright$ $\boldsymbol{X}$ -Werte begründen

In dieser Teilaufgabe sollst du begründen, dass $X$ nur die Werte $0$ , $2$ , $4$ oder $10$ annehmen kann. $X$ gibt hierbei den an den Spieler ausgezahlten Betrag in Euro an.

Der Spieler kann in einem Spiel verlieren oder gewinnen. Verliert der Spieler bekommt er $0$ Euro ausgezahlt. Gewinnt der Spieler bekommt er pro Wurf in diesem Spiel $2$ Euro ausgezahlt. Hierbei musst du beachten, dass ein Spieler nur dann gewinnt, wenn er genau die Punktzahl $10$ erreicht. Du musst dir also überlegen, welche Möglichkeiten es gibt, dass ein Spieler genau die Punktzahl $10$ erreicht.

Eine weitere Möglichkeit ist, dass der Spieler zweimal die Punktzahl $5$ würfelt. Somit würde der Spieler $4$ Euro ausgezahlt bekommen, da er zweimal gewürfelt hat.

Die letzte Möglichkeit ist, dass der Spieler fünfmal die Punktzahl $2$ würfelt. Dadurch würde der Auszahlungsbetrag auf $10$ Euro ansteigen.

Dies sind alle Möglichkeiten, die für den Auszahlungsbetrag auftreten können. Deshalb kann $X$ nur die Werte $0$ , $2$ , $4$ oder $10$ annehmen.

$\blacktriangleright$ Begründen, dass das Spiel nicht fair ist

In dieser Teilaufgabe sollst du begründen, dass das Spiel nicht fair ist. Dazu musst du den Erwartungswert berechnnen. Den Erwartungswert lässt sich mit folgender Formel berechnen:

$E(X)$ = $\displaystyle\sum\limits_{i=1}^{n} k_i \cdot P(X=k_i)$ = $k_1 \cdot P(X=k_1)$ + $k_2\cdot P(X=k_2)$ + $...$ + $k_n \cdot P(X=k_n)$

$X$ bezeichnet hierbei den ausgezahlten Betrag in Euro. Zuerst kannst du somit den Erwartungswert für den ausgezahlten Betrag berechnen. Um zu begründen, dass das Spiel nicht fair ist musst du anschließend noch den Einsatz von $1$ Euro abziehen. Damit das Spiel fair ist muss $E(X)=0$ gelten.

Für den Erwartungswert des Spiels folgt mit der angegeben Wahrscheinlichkeitsverteilung und dem Einsatz $S=1 €$ :

$E(X)=-\dfrac{44}{243} €$

Vollständige Lösung anzeigen

Somit beträgt der Erwartungswert $E(X)=- \dfrac{44}{243}€$ und dies ist ungleich Null. Deshalb ist das Spiel nicht fair.

$\blacktriangleright$ Auszahlungsbetrag verändern

In dieser Teilaufgabe sollst du untersuchen, ob bei einem unveränderten Einsatz von $1€$ der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair ist. Bezeichne hierbei den Auszahlungsbetrag pro Wurf mit $Y$ . Nun musst du den Auszahlungsbetrag pro Wurf abändern, sodass $E(X)=0$ gilt. Stelle dazu den Erwartungswert in Abhängigkeit des Auszahlungsbetrags dar und löse nach $Y$ auf.

$Y=\dfrac{486}{199} €$

Vollständige Lösung anzeigen

Somit gilt für einen Auszahlungsbetrag von $\dfrac{486}{199} €$ , dass das Spiel fair ist.

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür betimmen, dass der Spieler von $120$ Spielen mindestens $30$ und höchstens $50$ gewinnt. Somit ist die gesuchte Wahrscheinlichkeit $P(30 \leq X \leq 50)$ . Die Wahrscheinlichkeit, dass ein Spieler verliert liegt bei $P(X=0)=\dfrac{349}{486}$ . Entsprechend gilt für die Wahrscheinlichkeit $p$ , dass ein Spieler gewinnt mit dem Gegenereigniss:

$\begin{array}[t]{rll} p &=& 1 - P(X=0)\\[5pt] &=& 1 - \dfrac{349}{486}\\[5pt] &=& \dfrac{137}{486}\\[5pt] \end{array}$

Du kannst hierbei nun die gesuchte Wahrscheinlichkeit mit der Binomialverteilung berechnen. Die Wahrscheinlichkeit $P(30 \leq X \leq 50)$ kannst du außerdem wie folgt umschreiben:

$P(30 \leq X \leq 50) =\dotsc$

Vollständige Lösung anzeigen

Zudem ist gegeben, dass der Spieler insgessamt $n=120$ Spiele spielt. Verwende den binomcdf-Befehl deines CAS. Diesen findest du unter

Interaktiv $\to$ Verteilungsfkt. $\to$ Diskret $\to$ binomialCDf.

Für die Wahrscheinlichkeiten folgt mit deinem CAS:

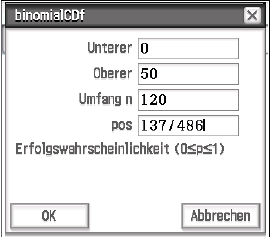Dialogfenster einer Software zur Berechnung der binomialen kumulierten Verteilungsfunktion.

Abb. 1: Eingetragene Daten

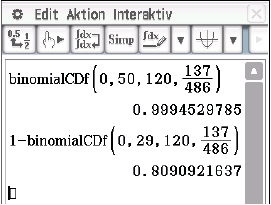Screenshot einer mathematischen Software mit Berechnungen zur binomialen kumulativen Verteilungsfunktion.

Abb. 2: Ergebnis

Somit beträgt die Wahrscheinlichkeit, dass der Spieler von $120$ Spielen mindestens $30$ und höchstens $50$ gewinnt $P(30 \leq X \leq 50)\approx 0,809$ .

$\blacktriangleright$ Wahrscheinlichkeit erläutern

In dieser Teilaufgabe sollst du erläutern welche Wahrscheinlichkeit mit dem Term $1- 19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ berechnet werden kann. Der Term $19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ gibt hierbei die Wahrscheinlichkeit dafür an, dass ein Spieler von $19$ Spielen einmal verliert und $18$ -mal gewinnt. Dies lässt sich auch durch die folgende Formel zur Berechnung der Wahrscheinlichkeit bei einer Binomialverteilung verdeutlichen:

$P(X=k) = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}.$

In diesem Fall gilt $k=1$ , $n=19$ und $p=\dfrac{349}{486}$ .

Der gesamte Term $1- 19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ bezeichnet das Gegenereignis des Terms $19 \cdot \dfrac{349}{486} \cdot \left(\dfrac{137}{486}\right)^{18}$ . Somit berechnet der gegebene Term die Wahrcheinlichkeit dafür, dass ein Spieler von $19$ Spielen nicht einmal verliert und nicht $18$ -mal gewinnt.

$\blacktriangleright$ Gleichung herleiten

In dieser Aufgabe sollst du eine Gleichung zur Bestimmung der Anzahl aller Kugeln in einer Urne herleiten. Hierfür hast du gegeben, dass sich neben anderen Kugeln genau fünf gelbe Kugeln befinden. Außerdem ist bekannt, dass wenn zwei Kugeln gleichzeitig aus der Urne gezogen werden, die Wahrscheinlichkeit eine gelbe zu bekommen $\dfrac{1}{3}$ beträgt. Du kannst hierbei zur Hilfe ein zweistufiges Baumdiagramm zeichnen mit den Pfaden gelb oder nicht gelb.

Bezeichne hierbei die Gesamtanzahl aller Kugeln in einer Urne mit $n$ . Somit folgt für die gesamte Anzahl aller nicht gelben Kugeln $n-5$ , da in der Urne genau $5$ gelbe Kugeln sind. Es handelt sich hierbei um Ziehen ohne Zurücklegen. Das bedeutet, dass sich beim zweiten Ziehen nur noch $n-1$ Kugeln in der Urne befinden.

Das Baumdiagramm mit den einzelnen Wahrscheinlichkeiten ergibt sich dann wie folgt:

Abb. 3: Baumdiagramm

Du hast in der Aufgabenstellung die Wahrscheinlichkeit dafür gegeben, dass eine der beiden gezogenen Kugeln gelb ist. Hierfür gibt es zwei Möglichkeiten, da du zuerst eine Kugel ziehen kannst, die nicht gelb ist und anschließend eine gelbe Kugel oder zuerst eine gelbe Kugel und anschließend eine nicht gelbe Kugel.

Für die Wahrscheinlichkeit $P$ , dass beim Ziehen von zwei Kugeln eine der beiden Kugeln gelb ist folgt somit:

$P=\dotsc$

Vollständige Lösung anzeigen

Da du hierbei gegeben hast, dass $P=\dfrac{1}{3}$ gilt, folgt der Term $\dfrac{1}{3}=2 \cdot \dfrac{5}{n} \cdot \dfrac{n-5}{n-1}$ für die Gesamtanzahl $n$ an Kugeln in der Urne.

Bildnachweise [nach oben]

[1]

[2]

[3]