Analysis

Aufgabe 1A

Gegeben ist die Schar der in $\mathbb R$ definierten Funktionen $f_a$ mit $f_a(x) = \dfrac{1}{a^3} x^3 - \dfrac{1}{a} x^2 + x$ und $a \in \mathbb{R}^+$ .

Skizziere den Graphen von $f_4$ in Abbildung 1.

Gib die Extrempunkte von $f_4$ an.

niedersachsen ga cas abi koordinatensystem

Abbildung 1

(5 BE)

Ermittle die Koordinaten der gemeinsamen Punkte der Graphen von $f_1$ und $f_4.$

Weise nach, dass es nur einen Punkt gibt, der auf allen Graphen der Schar liegt.

(5 BE)

Die Gleichung $f_a(x) = 0$ hat in Abhängigkeit von $a$ die Lösungen $\dfrac{a^2 - \sqrt{a^3 \cdot (a - 4)}}{2}$ und $0$ und $\dfrac{a^2 + \sqrt{a^3 \cdot (a - 4)}}{2}.$

Gib die Anzahl der Nullstellen von $f_a$ in Abhängigkeit von $a$ an und begründe deine Angabe anhand der obigen Terme.

(6 BE)

Der Graph jeder Funktion $f_a$ hat genau einen Wendepunkt.

Bestimme den Wert von $a$ zu dem Wendepunkt mit der größten $y$ -Koordinate.

(5 BE)

Für ein Umweltschutzprojekt nehmen zwei Unterwasserdrohnen $U_1$ und $U_2$ in einem See Messungen in unterschiedlichen Tiefen vor. Sie bewegen sich nur in vertikaler Richtung, d.h. senkrecht zur Wasseroberfläche des Sees. Ihre Geschwindigkeiten werden für $0 \leq t \leq 30$ durch die in $\mathbb R$ definierten Funktionen $v$ bzw. $w$ beschrieben, wobei gilt:

$v(t) = -\dfrac{6}{25} t \cdot (4t - 25) \cdot \mathrm e^{-\frac{1}{5}t} \quad$ und $\quad w(t) = \dfrac{1}{216} t^3 - \frac{1}{6} t^2 + t$

Dabei ist $t$ die seit Beobachtungsbeginn vergangene Zeit in Minuten. $v(t)$ ist die Geschwindigkeit von $U_1$ in Meter pro Minute und $w(t)$ ist die Geschwindigkeit von $U_2$ in Meter pro Minute. Wenn die Geschwindigkeit positiv ist, steigt die Unterwasserdrohne.

Bestimme die Koordinaten des Tiefpunktes des Graphen von $v$ und interpretiere die Werte im Sachkontext.

(4 BE)

Mit $\( v$ wird die erste Ableitungsfunktion von $v$ bezeichnet. Innerhalb eines bestimmten Zeitraums gilt für jeden Zeitpunkt $t$ die folgende Aussage: $v(t) \lt 0$ und $\( v$

Interpretiere dies in Bezug auf die Bewegung von $U_1$ in diesem Zeitraum.

(3 BE)

Im Beobachtungszeitraum beträgt der geringste Abstand von $U_1$ zur Wasseroberfläche des Sees 10 Meter.

Ermittle den Abstand von $U_1$ zur Wasseroberfläche zu Beobachtungsbeginn.

(6 BE)

$U_2$ ist zu Beobachtungsbeginn 5 Meter tiefer als $U_1$ und steigt langsamer als $U_1$ . Der Graph in Abbildung 2 zeigt für die ersten Minuten des Beobachtungszeitraums die zeitliche Entwicklung des vertikalen Abstands der beiden Unterwasserdrohnen zueinander. Im dargestellten Bereich hat der Graph nur einen Hochpunkt $H(t_H \mid y_H).$

Erläutere, wie man $t_H$ anhand der Graphen von $v$ und $w$ ermitteln kann, und gib einen Term zur Berechnung von $y_H$ an.

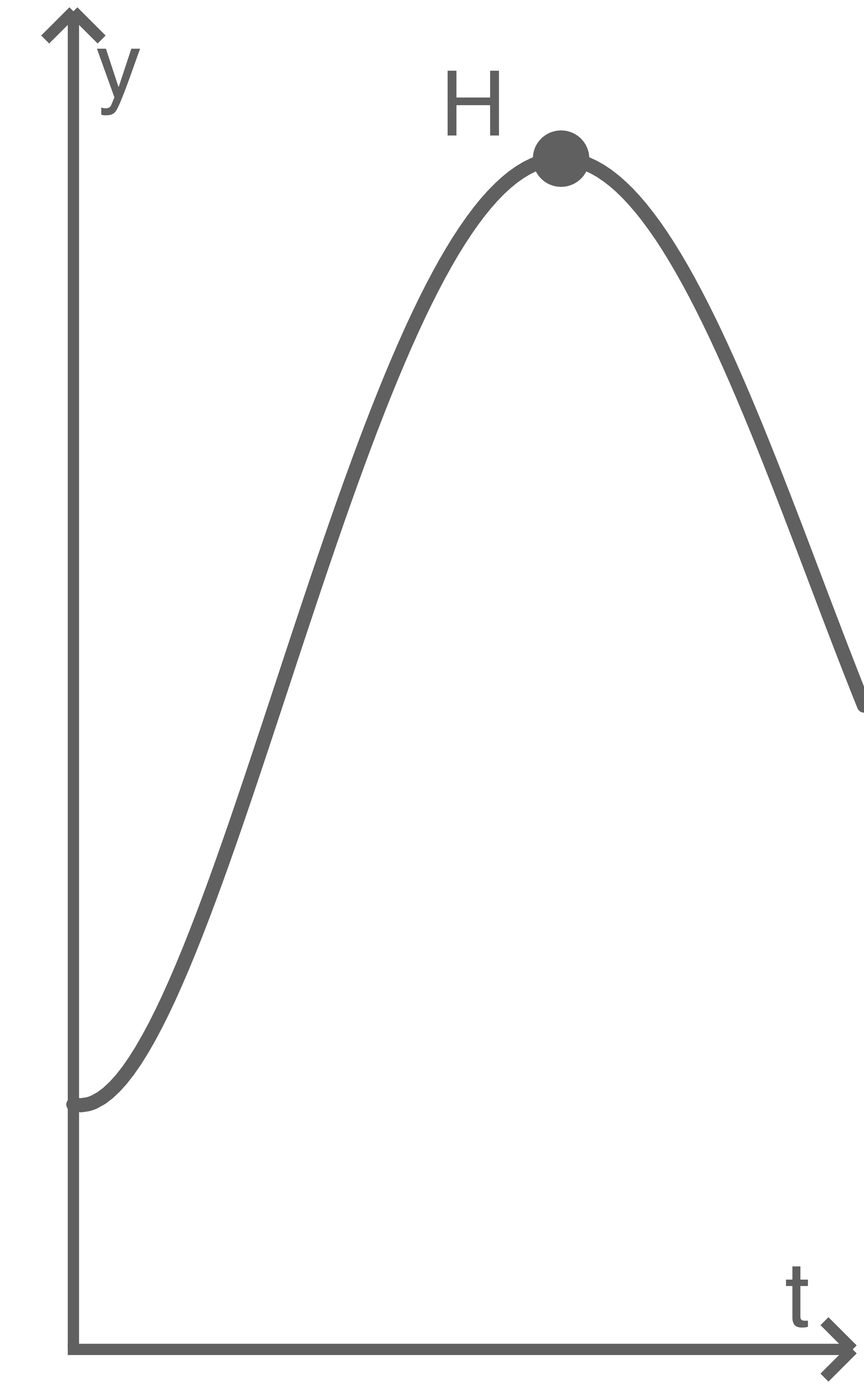
Abbildung 2

(6 BE)

Aufgabe 1B

Die zeitliche Entwicklung der Blutalkoholkonzentration (BAK) kann für eine bestimmte Person nach dem Verzehr von zwei Gläsern Wein durch die auf $\mathbb R$ definierte Funktion $f$ mit $f(t) = 1,081 \cdot (1 - \mathrm{e}^{-t}) - 0,15 \cdot t$ beschrieben werden. Dabei gibt $t$ die Zeit nach dem Trinken in Stunden an und $f(t)$ die BAK in Gramm pro Kilogramm $\left(\frac{\text{g}}{\text{kg}}\right).$ Es soll vereinfacht davon ausgegangen werden, dass die gesamte Menge Wein auf einmal konsumiert wird.

Gib die Nullstellen von $f$ an.

Begründe, dass das Intervall $[0;7,2]$ eine angemessene Einschränkung des Definitionsbereichs der Funktion $f$ für den Sachzusammenhang ist.

(3 BE)

Berechne die maximale BAK der betrachteten Person.

Bei einer BAK von $0,5 \,\frac{\text{g}}{\text{kg}}$ oder mehr darf die Person in Deutschland kein Auto mehr fahren.

Bestimme den Zeitraum, in dem die Person nicht Auto fahren darf.

(6 BE)

Mit Hilfe einer linearen Funktion können Näherungswerte für die BAK berechnet werden.

Für jede Person ergibt sich je nach individuellen Eigenschaften und konsumierter Alkoholmenge eine andere lineare Funktion. Der $y$ -Achsenabschnitt des Graphen der linearen Funktion wird als theoretische maximale BAK bezeichnet.

Für die betrachtete Person wird die auf $\mathbb R$ definierte Funktion $h$ mit $h(t)=1,081-0,15\cdot t$ verwendet. Dabei beschreibt $t$ die Zeit nach dem Trinken in Stunden und $h(t)$ Näherungswerte der BAK in $\frac{\text{g}}{\text{kg}}.$

Zeige, dass die theoretische maximale BAK für die betrachtete Person $1,081\,\frac{\text{g}}{\text{kg}}$ beträgt.

Zur Bestimmung der linearen Funktion für eine zweite Person werden zwei Messungen durchgeführt: 4 Stunden nach dem Verzehr beträgt die BAK $0,48 \,\frac{\text{g}}{\text{kg}}$ und weitere 30 Minuten später $0,39 \,\frac{\text{g}}{\text{kg}}.$

Berechne damit die theoretische maximale BAK der zweiten Person.

(5 BE)

Begründe mit Hilfe des Terms von $f ,$ dass die Werte der BAK der ersten betrachteten Person zu jedem Zeitpunkt kleiner sind als ihre theoretische maximale BAK.

(3 BE)

Zeige, dass $f$ eine Lösung der Differenzialgleichung

$\(f$

mit $k=1,$ $G=1,081$ und $m=0,15$ ist.

(4 BE)

Für verschiedene Personen ergeben sich individuelle zeitliche Verläufe der BAK.

Für $0 \lt m \lt 1,081$ werden die auf $\mathbb R$ definierten Funktionen $f_m$ mit $f_m(t) = 1,081 \cdot (1 - \mathrm e^{-t}) - m \cdot t$ betrachtet. $t$ beschreibt die Zeit nach dem Trinken in Stunden und $f_m(t)$ die BAK in $\frac{\text{g}}{\text{kg}}.$

Bestimme alle Werte von $m ,$ so dass die BAK zu keinem Zeitpunkt den Wert von $0,5 \,\frac{\text{g}}{\text{kg}}$ überschreitet.

(7 BE)

Unabhängig vom Sachkontext wir die auf $\mathbb R$ definierte Funktionenschar $p_a$ für $a\gt 0$ betrachtet mit $p_a(x)=2\cdot(1-\mathrm e^{-a\cdot x})-\dfrac{1}{5}\cdot x.$

Zeige, dass jede Funktion der Schar ein lokales Maximum an der Stelle $x = \frac{\ln(10 \cdot a)}{a}$ hat.

Begründe, dass die $x$ -Koordinaten der Hochpunkte für $a \gt \dfrac{\mathrm e}{10}$ mit wachsenden Werten von $a$ kleiner werden.

(7 BE)

Der Inhalt der Fläche zwischen den Graphen von $p_{0,5}$ und $p_3$ auf dem Intervall $[0;1]$ soll an der Stelle $u$ durch eine Parallele zur $y$ -Achse halbiert werden.

Bestimme $u .$

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1A

Graph skizzieren

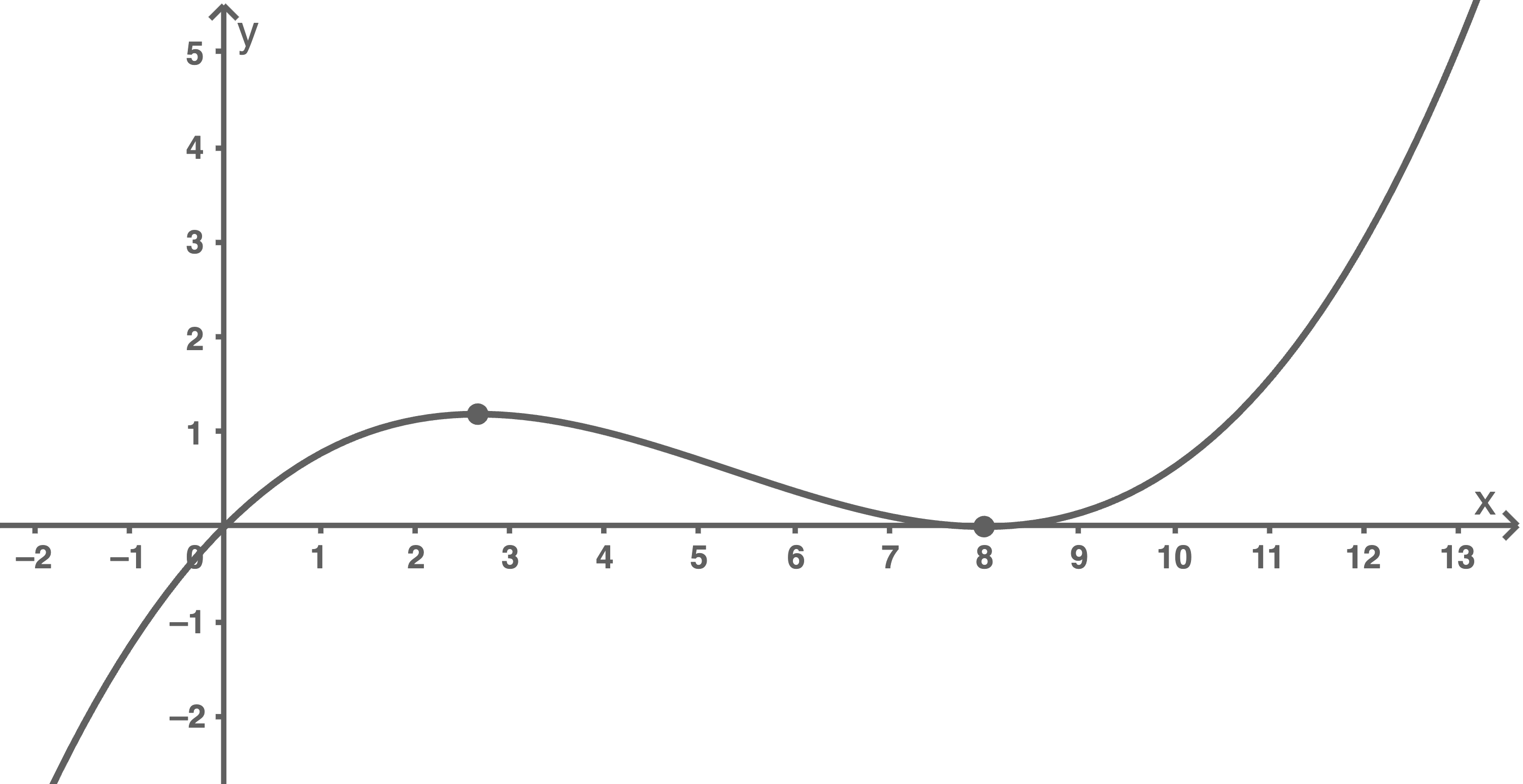Mathematisches Diagramm mit einer Kurve im Koordinatensystem, zeigt den Verlauf von y in Abhängigkeit von x.

Abbildung 1

Extrempunkte angeben

Die Extrempunkte können aus dem Graphen abgelesen werden und besitzen die Koordinaten $T(8 \mid 0)$ sowie etwa $H(2,7 \mid 1,2).$

Koordinaten ermitteln

Gesucht sind die Punkte, an denen gilt:

Mit dem solve-Befehl des CAS ergibt sich:

$x_1=0$ und $x_2\approx 0,76$

$y$ -Koordinaten bestimmen:

$\begin{array}[t]{rll} f_1(0)&=& 0^3- 0^2+0 & \\[5pt] &=& 0 \end{array}$

$\begin{array}[t]{rll} f_1(0,76)&=& 0,76^3- 0,76^2+0,76 & \\[5pt] &\approx& 0,62 \end{array}$

Die gemeinsamen Punkte von $f_1$ und $f_4$ besitzen somit die Koordinaten $P_1(0 \mid 0)$ und $P_2(0,76 \mid 0,62).$

Gemeinsamen Punkt nachweisen

Da $f_a(0)=0$ unabhängig von $a$ gilt, liegt der Punkt $(0 \mid 0)$ auf allen Graphen der Schar.

Ein weiterer möglicher gemeinsamer Punkt wäre $P_2(0,76 \mid 0,62).$

Vergleich mit anderen Funktionen der Schar liefert allerdings:

$f_3\left(0,76\right) \approx 0,58 \neq f_1\left(0,76\right)$

Da dieser Punkt neben dem Ursprung der einzige gemeinsame Punkt von $f_1$ und $f_4$ ist, liegt nur der Ursprung und somit genau ein Punkt auf allen Graphen der Schar.

Die Anzahl der Nullstellen hängt von dem Radikanden, also dem Term unter der Wurzel, ab:

$a^3(a-4)\lt 0 \quad \rightarrow$ eine Nullstelle $(x_1=0)$
$a^3(a-4) = 0 \quad \rightarrow$ zwei Nullstellen $\left(x_1=0,\; x_2=\dfrac{a^2}{2}\right)$
$a^3(a-4)\gt 0 \quad \rightarrow$ drei Nullstellen

Die Graphen von $f_a$ besitzen somit für $a \lt 4$ eine Nullstelle, für $a=4$ zwei Nullstellen und für $a\gt 4$ drei Nullstellen.

1. Schritt: Wendestelle bestimmen

Notwendige Bedingung für Wendepunkte anwenden:

$\(\begin{array}[t]{rll} f_a$

Da vorausgesetzt ist, dass der Graph der Funktion $f_a$ genau einen Wendepunkt hat, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.

2. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

Für die $y$ -Werte an der Stelle $x=\dfrac{a^2}{3}$ ergibt sich mit dem CAS:

Rechenweg anzeigen

$f_a\left(\dfrac{a^2}{3}\right) = -\dfrac{2}{27} a^3+\dfrac{1}{3} a^2$

3. Schritt: Ableitung bestimmen

Ableiten nach $a$ ergibt:

$\(\begin{array}[t]{rll} f_a$

4. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_a$

Mit dem CAS folgt $a_1=0$ und $a_2=3.$

Da $a \in \mathbb{R}^+,$ ist $a=3$ die einzige mögliche Extremstelle.

Aus der Aufgabenstellung geht hervor, dass eine größte $y$ -Koordinate und somit genau ein Maximum existiert. Dieses muss sich also bei $a=3$ befinden.

Der Wendepunkt hat somit für $a=3$ die größte $y$ -Koordinate.

Koordinaten bestimmen

Dem Graphen kann der Tiefpunkt mit den Koordinaten $T\left(14 \mid -6,3\right)$ entnommen werden.

Werte interpretieren

Die Unterwasserdrohne $U1$ hat etwa 14 Minuten nach Beobachtungsbeginn die größte Sinkgeschwindigkeit von etwa $6,3 \dfrac{\text{m}}{\text{min}}.$

Wegen $v(t)\lt0$ sinkt $U1.$ Wegen $\(v$ ist die momentane Änderungsrate ihrer Geschwindigkeit positiv.

Die Unterwasserdrohne $U1$ sinkt in diesem Zeitraum somit immer langsamer.

1. Schritt: Nullstellen berechnen:

$\begin{array}[t]{rll} v(t)&=& 0 & \\[5pt] -\dfrac{6}{25} t \cdot(4 t-25) \cdot \mathrm{e}^{-\frac{1}{5} t}&=& 0 &\quad \scriptsize \mid\; :\mathrm{e}^{-\frac{1}{5} t} \\[5pt] -\dfrac{6}{25} t \cdot(4 t-25) &=& 0 & \\[5pt] \end{array}$

Mit dem CAS folgt:

$t_1=0$ und $t_2=6,25.$

2. Schritt: Abstand bestimmen

Aus dem Graphen von $v$ ergibt sich, dass $v(t)\gt 0$ für $0\lt t \lt 6,25$ und $v(t)\lt 0$ für $6,25\lt t\lt 30$ gilt.

$U1$ hat somit 6,25 Minuten nach Beobachtungsbeginn den kleinsten Abstand von 10 Metern zur Wasseroberfläche.

Für die Strecke, die $U1$ seit Beobachtungsbeginn bis zum Zeitpunkt $t=6,25$ zurückgelegt hat, folgt mit dem CAS:

$\displaystyle\int_{0}^{6,25}v(t)\;\mathrm dt \approx 21,7$

Der Abstand von $U1$ zur Wasseroberfläche beträgt zu Beobachtungsbeginn somit ca. $10+21,7=31,7$ Meter.

Bei der $t$ -Koordinate $t_S$ des einzigen Schnittpunkts der Graphen von $v$ und $w$ innerhalb der ersten Minuten wechselt $w(t)\lt v(t)$ zu $v(t)\lt w(t)$ .

Somit nimmt der vertikale Abstand von $U1$ und $U2$ bis zum Zeitpunkt $t_S$ zu und danach wieder ab.

Folglich ist $t_H=t_S.$

Ein Term zur Berechnung von $y_h$ ist somit:

$y_H=5+\displaystyle\int_{0}^{t_s}v(t)-w(t)\;\mathrm dt$

Lösung 1B

Nullstellen angeben

Die Nullstellen können aus dem Graphen der Funktion $f$ abgelesen werden. Es ergeben sich:

$t_1=0$ und $t_2 \approx 7,20$

Intervall begründen

Da die Blutalkoholkonzentration nur positive Werte annehmen kann, sollte der Definitionsbereich auf das Intervall zwischen den Nullstellen eingeschränkt werden, in welchem der Graph oberhalb der $x$ -Achse verläuft.

Dies ist genau das Intervall $[0; 7,2].$

Maximale BAK berechnen

Notwendige Bedingung für Extremstellen anwenden:

$\begin{array}[t]{rll} f(t)&=& 0 & \\[5pt] 1,081 \cdot\left(1-\mathrm{e}^{-t}\right)-0,15 \cdot t&=& 0 &\\[5pt] \end{array}$

Mit dem solve-Befehl des CAS ergibt sich $t \approx 1,975.$

Funktionswert berechnen:

$f(1,975) \approx 0,63$

Die maximale BAK beträgt somit etwa $0,63 \dfrac{\text{g}}{\text{kg}}.$

Zeitraum bestimmen

Es gilt:

$\begin{array}[t]{rll} f(t) &=& 0,5 &\quad \scriptsize \mid\; CAS\\[5pt] t_1&=& 0,88 &\\[5pt] t_2 &=& 3,69 \end{array}$

Im Zeitraum von etwa 0,88 Stunden bis 3,69 Stunden nach dem Trinken darf die Person somit kein Auto fahren.

Maximale BAK nachweisen

Laut der Aufgabenstellung entspricht die maximale BAK dem $y$ -Achsenabschnitt des Graphen von $h.$

Für diesen gilt:

$\begin{array}[t]{rll} h(0) &=& 1,081-0,15 \cdot 0& \\[5pt] &=& 1,081 \; \left[\dfrac{\text{g}}{\text{kg}}\right] \end{array}$

Theoretische maximale BAK berechnen

Die Steigung des Graphen der entsprechenden linearen Funktion beträgt $\dfrac{0,39-0,48}{0,5}=-0,18.$

Der $y$ -Achsenabschnitt ergibt sich damit zu:

$0,48+0,18 \cdot 4=1,2$

Die theoretische maximale BAK ist somit $1,2 \; \dfrac{\text{g}}{\text{kg}}.$

Für $t \geq 0$ gilt $1-\mathrm{e}^{-t} \lt 1.$

Damit folgt $1,081 \cdot\left(1-\mathrm{e}^{-t}\right)-0,15 \cdot t\lt 1,081.$

Somit sind die Werte der BAK der ersten betrachteten Person zu jedem Zeitpunkt $t\geq 0$ kleiner als die theoretisch maximale BAK von $1,081 \; \dfrac{\text{g}}{\text{kg}}.$

Ableitung von $f$ bestimmen:

$\(\begin{array}[t]{rll} f$

Einsetzen der gegebenen Parameter in die Differenzialgleichung liefert:

$\( f$

Rechenweg anzeigen

Da die Terme somit übereinstimmen, ist $f$ eine Lösung der Differenzialgleichung mit den gegebenen Werten für $k,G$ und $m.$

1. Schritt: Maximum berechnen

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} f_m$

Hinreichende Bedingung für Extremstellen anwenden:

$\(f_m$

Somit besitzen alle Graphen der Schar ein lokales Maximum an der Stelle $t=\ln \left(\dfrac{1081}{1000 \cdot m}\right).$

Werte bestimmen

Es gilt:

$\begin{array}[t]{rll} f_m\left(\ln \left(\dfrac{1081}{1000 \cdot m}\right)\right)&=& 0,5 &\quad \scriptsize \mid\; CAS \\[5pt] m_1&\approx & 0,227& \\[5pt] m_2& \approx &2,277 & \\[5pt] \end{array}$

Darstellen des Graphen von $f_m\left(\ln \left(\dfrac{1081}{1000 \cdot m}\right)\right)$ mit dem CAS liefert, dass die BAK für alle $m$ mit $m_1 \lt m \lt m_2$ kleiner als $0,5$ ist.

Wegen $0 \lt m \lt 1,081$ ergeben sich die gesuchten Werte von $m$ also zu:

$0,227 \lt m \lt 1,081$

Maximum nachweisen

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} p_a$

Hinreichende Bedingung für Extremstellen anwenden:

Für die zweite Ableitung gilt: $\(\; p_a$

Somit gilt auch insbesondere $\(p_a$

An der Stelle $x = \dfrac{\ln (10 \cdot a)}{a}$ besitzt somit jede Funktion ein lokales Maximum.

Begründung

Darstellen des Graphen der Funktion $q$ mit $q(a)=\dfrac{\ln (10-a)}{a}$ mit dem CAS zeigt, dass $q$ bei $a=\dfrac{\mathrm{e}}{10}$ das einzige Maximum hat.

Für $a\gt\dfrac{\mathrm{e}}{10}$ werden deshalb die $x$ -Koordinaten der Hochpunkte für wachsende Werte von $a$ kleiner.

Darstellen der Graphen mit dem CAS liefert, dass für alle $0\leq x \leq 1$ gilt:

$p_{0,5}(x)\lt p_3(x)$

Es soll nun also gelten:

Gleichung anzeigen

Das CAS liefert:

$u \approx 0,59$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?