Aufgabe 3B

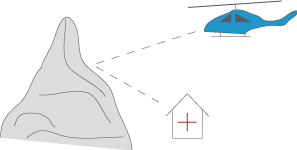
Drei blaue Hubschrauber fliegen zu einem Haus neben einem Berg.

Eine Gruppe Bergsteiger gerät am Berg in Not und funkt nach Hilfe.
In einem passenden Koordinatensystem befindet sich die Bergwacht im Ursprung $O(0\mid0\mid0)$ .
Ein Hubschrauber befindet sich im Punkt $H(-4\mid6\mid1)$ . Alle Koordinaten haben die Einheit km.

a) Der Notruf der Bergsteiger wird von der Bergwacht aus der Richtung $\vec{u}=\begin{pmatrix}1\\-3\\2\end{pmatrix}$ aufgenommen.

Der Hubschrauber nimmt den Notruf aus der Richtung $\vec{v}=\begin{pmatrix}2\\-4\\1\end{pmatrix}$ auf.
Berechnen Sie die Koordinaten des Punktes $N$ , in dem sich die Bergsteigergruppe aufhält.

(Zur Kontrolle: $N(2\mid-6\mid4)$ )

Der Hubschrauber fliegt sofort zum Aufenthaltsort der Bergsteigergruppe. Vereinfachend wird angenommen, dass seine Geschwindigkeit konstant $250\frac{\text{km}}{\text{h}}$ beträgt.

Berechnen Sie seine Flugzeit bis zum Eintreffen im Punkt $N$ in Minuten.

(9P)

Der Hubschrauber nimmt die Bergsteigergruppe auf und fliegt vom Aufenthaltsort in Punkt $N$ zur Bergwacht. Dabei fliegt er die Bergwacht jedoch nicht direkt an, sondern er fliegt zunächst zu einem Punkt $P$ und von dort weiter zur Bergwacht.

b) Der Hubschrauber fliegt vom Punkt $N$ aus zunächst mit dem Kurs $\vec{k}=\begin{pmatrix}-1\\0\\-2\end{pmatrix}$ bis zum Punkt $P$ und ändert dort seinen Kurs zu $\overrightarrow{m}=\begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$ .

Bestimmen Sie die Koordinaten des Punktes $P$ .

(Zur Kontrolle: $P(1,5\mid-6\mid3)$ )

Berechnen Sie den Winkel, unter dem der Hubschrauber seinen Kurs im Punkt $P$ ändert.

(8P)

c) Der Pilot überlegt eine alternative Route von $N$ über einen Punkt $P_{z}(1,5\mid-6\mid z)$ zur Bergwacht. Er möchte so fliegen, dass er seinen Kurs in $P_z$ unter einem Winkel von 90° ändert.
Untersuchen Sie, ob es entsprechende Werte für $z$ gibt.

(7P)

(24P)

a) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{N}$ , in dem sich die Bergsteigergruppe befindet

Der Notruf der Bergsteiger wird von der Bergwacht aus der Richtung $\vec{u}=\begin{pmatrix}1\\-3\\2\end{pmatrix}$ aufgenommen. Der Hubschrauber nimmt den Notruf aus der Richtung $\vec{v}=\begin{pmatrix}2\\-4\\1\end{pmatrix}$ auf.
Du sollst die Koordinaten des Punktes $N$ , in dem sich die Bergsteigergruppe aufhält, berechnen. Lege dafür eine Gerade durch den Ort der Bergwacht und eine zweite Gerade durch den Aufenthaltsort des Hubschraubers. Anschließend kannst du den Schnittpunkt dieser beiden Geraden berechnen. Die Richtungsvektoren der Geraden sind dir in der Aufgabenstellung gegeben:

Bergwacht: $\vec{x} = O + s\cdot \vec{u} = \begin{pmatrix}0\\0\\0\end{pmatrix} + s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}$

Hubschrauber: $\vec{x} = H + t\cdot \vec{v} = \begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}$

Um den Aufenthaltsort der Bergsteigergruppe zu bestimmen, musst du den Schnittpunkt der beiden Geraden berechnen.

$\begin{array}{rll} s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}&=&\begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}& \end{array}$

Dafür kannst du deinen Taschenrechner nutzen.

menu: 7: 1: 1:

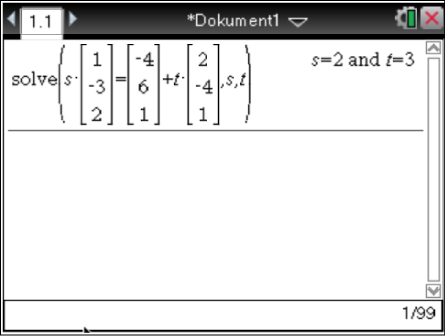Mathematische Gleichung zur Lösung von Variablen s und t in einer Matrixdarstellung.

Daraus folgt $s=2$ und $t = 3$ . Das Einsetzen von $s$ oder $t$ in die jeweilige Geradengleichung liefert dann den Schnittpunkt der Geraden. Setze also $s$ in die Geradengleichung der Bergwacht ein:

$N = 2\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = \begin{pmatrix}2\\-6\\4\end{pmatrix}$

Der Punkt $\boldsymbol{N(2\mid -6\mid 4)}$ gibt den Aufenthaltsort der Bergsteigergruppe an.

$\blacktriangleright$ Flugzeit berechnen

Du sollst seine Flugzeit bis zum Eintreffen im Punkt $N$ in Minuten berechnen. Vereinfachend wird angenommen, dass seine Geschwindigkeit konstant $250\frac{\text{km}}{\text{h}}$ beträgt.

Berechne dafür zuerst du Länge der Strecke $\overline{HN}$ über den Betrag des entsprechenden Verbindungsvektors:

$\mid \overline{HN} \mid = \left|\begin{pmatrix}6\\-12\\3\end{pmatrix}\right| = \sqrt{36 + 144 + 9} = \sqrt{189} = 13,75$ km

Die Entfernung vom Hubschrauber zur Bergsteigergruppe beträgt 13,75 km.
Die Zeit bis der Hubschrauber eintrifft kannst du mithilfe der angegebenen Geschwindigkeit berechnen:

$\dfrac{13,75 \text{km}}{250 \frac{\text{km}}{\text{h}}} = 0,055 \text{h}$

Rechne die Stundenangabe jetzt noch in Minuten um, indem du das Ergebnis mit 60 multiplizierst:

$t = 0,055 \cdot 60 = 3,3$ min

Der Hubschrauber braucht also 3,3 Minuten um zum Ort der Bergsteiger zu gelangen.

b) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{P}$ bestimmen

Du sollst die Koordinaten des Punktes $P$ bestimmen. Lege dafür eine Gerade $g_1$ durch den Punkt $N$ mit Richtung $\vec{k}$ und eine Gerade $g_2$ durch $O$ mit der Richtung $\overrightarrow{m}$ . Der Punkt $P$ ist gerade der Schnittpunkt der beiden Geraden.

$g_1: \vec{x} = \overrightarrow{ON} + t\cdot \vec{k} = \begin{pmatrix}2\\-6\\4\end{pmatrix} + t\cdot \begin{pmatrix}-1\\0\\-2\end{pmatrix}$

$g_2: \vec{x} = \overrightarrow{O} + u\cdot \overrightarrow{m} = u\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$

Setze diese beiden Geradengleichungen nun gleich um den Schnittpunkt zu bestimmen:

$\begin{array}{rcll} \begin{pmatrix}2\\-6\\4\end{pmatrix} + t\cdot \begin{pmatrix}-1\\0\\-2\end{pmatrix}&=&u\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}& \end{array}$

Du kannst dieses lineare Gleichungssystem mit deinem Taschenrechner lösen:

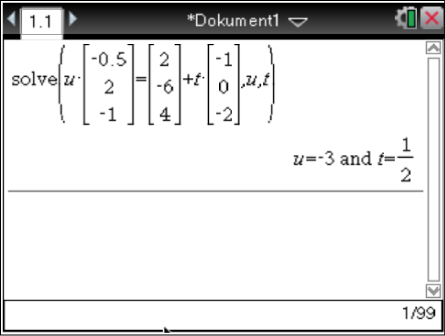Mathematische Gleichung zur Lösung eines Systems mit Variablen u und t in einem Dokument.

Es folgt $u=-3$ und $t=0,5$ .

Setze $u$ oder $t$ nun in die passende Gerade ein, um die Koordinaten von $P$ zu berechnen.

$P = (-3) \cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix} = \begin{pmatrix}1,5\\-6\\3\end{pmatrix}$

Die gesuchten Koordinaten sind gegeben durch $\boldsymbol{P(1,5\mid -6\mid 3)}$ .

$\blacktriangleright$ Winkel berechnen

Der gesuchte Winkel ist der Winkel zwischen den Geraden $g_1$ und $g_2$ . Den Winkel zwischen zwei Geraden berechnest du mit folgender Formel:

$\boldsymbol{\alpha = \arccos\left(\dfrac{\mid \overrightarrow{a_1} \cdot \overrightarrow{a_2}\mid}{\mid \overrightarrow{a_1}\mid \cdot \mid \overrightarrow{a_2}\mid}\right)}$

Wobei $\overrightarrow{a_1}$ und $\overrightarrow{a_2}$ die Richtungsvektoren der Geraden sind. Die Richtungsvektoren der Geraden sind $\vec{k}$ und $\overrightarrow{m}$ . Berechne also den Winkel, indem du zunächst die benötigten Beträge und das Skalarprodukt berechnest:

$\mid \vec{k} \cdot \overrightarrow{m}\mid$ $= \left|\begin{pmatrix}-1\\0\\-2\end{pmatrix} \cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}\right|$ $= \mid (-1)\cdot (-0,5) + 0 \cdot 2 + (-2) \cdot (-1)\mid = 2,5$
$\mid \vec{k}\mid$ $= \left|\begin{pmatrix}-1\\0\\-2\end{pmatrix}\right|$ $= \sqrt{(-1)^2 + 0^2 + (-2)^2}$ $= \sqrt{5}$
$\mid \overrightarrow{m}\mid$ $= \left|\begin{pmatrix}-0,5\\2\\-1\end{pmatrix}\right|$ $= \sqrt{(-0,5)^2 + 2^2 + (-1)^2}$ $= \sqrt{5,25}$

Für den Winkel ergibt sich dann:

$\alpha = \arccos\left(\dfrac{\mid \vec{k} \cdot \overrightarrow{m}\mid}{\mid \vec{k}\mid \cdot \mid \overrightarrow{m}\mid}\right)$ $= \dfrac{2,5}{\sqrt{5}\cdot \sqrt{5,25}}= 60,8\;^{\circ}$

Der Hubschrauber ändert seinen Kurs im Punkt $P$ um $\boldsymbol{60,8\;^{\circ}}$ .

c) $\blacktriangleright$ Den Wert $\boldsymbol{z}$ bestimmen

Der Kurs in $P_z(1,5\mid-6\mid z)$ soll sich unter einem Winkel von $90\;^{\circ}$ ändern. Du sollst nun alle Werte für $z$ bestimmen.

Der Winkel von $90\;^{\circ}$ bedeutet gerade, dass das Skalarprodukt der beiden Richtungen 0 ergibt. Berechne also das Skalarprodukt in Abhängigkeit von $z$ und setze anschließend mit $0$ gleich um die möglichen Werte für $z$ zu bestimmen.

Die beiden Richtungen sind gegeben durch:

$\overrightarrow{NP_z} = \begin{pmatrix}1,5\\-6\\z\end{pmatrix} - \begin{pmatrix}2\\-6\\4\end{pmatrix}$ $= \begin{pmatrix}-0,5\\0\\z-4\end{pmatrix}$

$\overrightarrow{P_z O} = \begin{pmatrix}0\\0\\0\end{pmatrix}-\begin{pmatrix}1,5\\-6\\z\end{pmatrix}$ $= \begin{pmatrix}-1,5\\6\\-z\end{pmatrix}$

Berechne nun das Skalarprodukt der beiden Richtungen in Abhängigkeit von $z$ :

$\mid \overrightarrow{NP_z} \cdot \overrightarrow{P_z O}\mid$ $= \left|\begin{pmatrix}-0,5\\0\\z-4\end{pmatrix} \cdot \begin{pmatrix}-1,5\\6\\-z\end{pmatrix}\right|$ $=\mid (-0,5)\cdot (-1,5) + 0 \cdot 6 + (z-4) \cdot (-z) \mid$ $= \mid -z^2 + 4z +0,75\mid$

Dieses Skalarprodukt soll 0 sein, berechne also die Nullstellen der quadratischen Funktion mit dem solve-Befehl deines Taschenrechners.

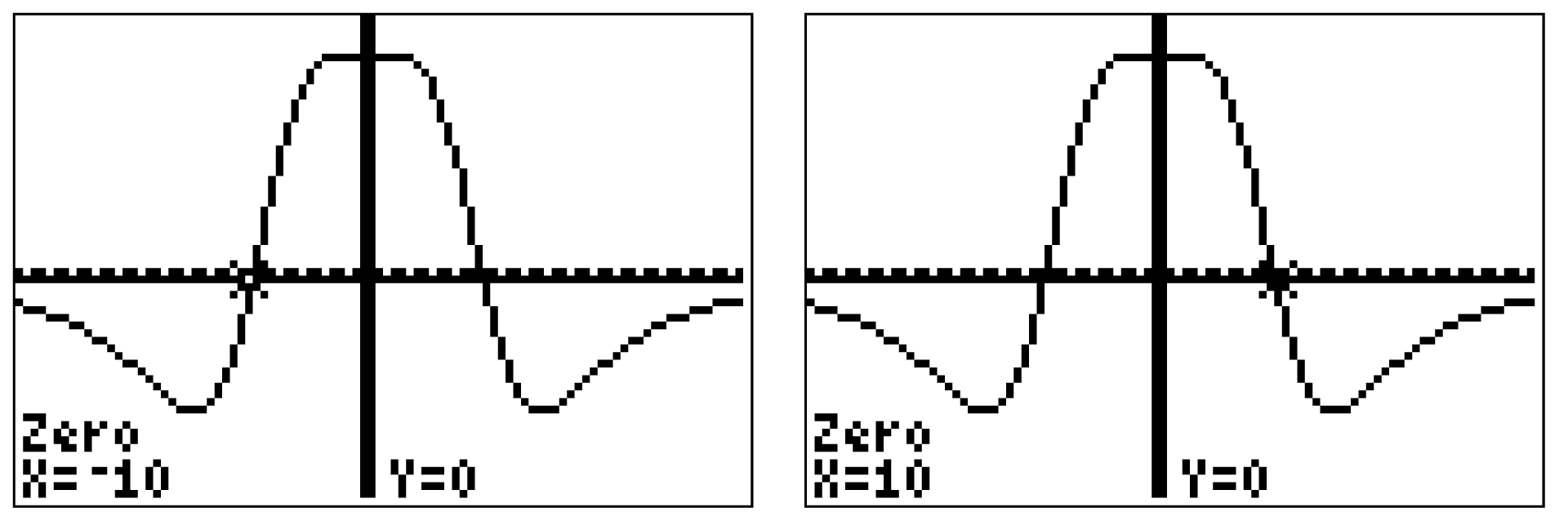Zwei Diagramme mit grafischen Darstellungen von Funktionen, jeweils mit Achsenbeschriftungen.

Du erhältst zwei Nullstellen $z_1 = -0,179$ und $z_2 = 4,179$ . Es existieren somit zwei passende Werte für $\boldsymbol{z}$ .

a) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{N}$ , in dem sich die Bergsteigergruppe befindet

Bergwacht: $\vec{x} = O + s\cdot \vec{u} = \begin{pmatrix}0\\0\\0\end{pmatrix} + s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}$

Hubschrauber: $\vec{x} = H + t\cdot \vec{v} = \begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}$

Um den Aufenthaltsort der Bergsteigergruppe zu bestimmen, musst du den Schnittpunkt der beiden Geraden berechnen.

$\begin{array}{rll} s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}&=&\begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}& \end{array}$

Daraus ergibt sich folgendes lineares Geichungssystem:

$\begin{array}{l@{\qquad}*{3}{rc}r@{\qquad}l} (1)&s&=&-4&+&2t&&\\ (2)&-3\cdot s&=&6&-&4t&&&\\ (3)&2 \cdot s&=&1&+&t&&& \end{array}$

Um dieses zu lösen kannst du deinen Taschenrechner nutzen. Den Befehl für ein Gleichungssystem findest du unter

Keyboard 2D

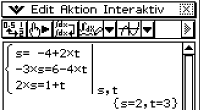Mathematische Gleichungen und Interaktionen auf einem Bildschirm dargestellt.

Daraus folgt $s=2$ und $t = 3$ . Das Einsetzen von $s$ oder $t$ in die jeweilige Geradengleichung liefert dann den Schnittpunkt der Geraden. Setze also $s$ in die Geradengleichung der Bergwacht ein:

$N = 2\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = \begin{pmatrix}2\\-6\\4\end{pmatrix}$

Der Punkt $\boldsymbol{N(2\mid -6\mid 4)}$ gibt den Aufenthaltsort der Bergsteigergruppe an.

$\blacktriangleright$ Flugzeit berechnen

Du sollst seine Flugzeit bis zum Eintreffen im Punkt $N$ in Minuten berechnen. Vereinfachend wird angenommen, dass seine Geschwindigkeit konstant $250\frac{\text{km}}{\text{h}}$ beträgt.

Berechne dafür zuerst du Länge der Strecke $\overline{HN}$ über den Betrag des entsprechenden Verbindungsvektors:

$\mid \overline{HN} \mid = \left|\begin{pmatrix}6\\-12\\3\end{pmatrix}\right| = \sqrt{36 + 144 + 9} = \sqrt{189} = 13,75$ km

Die Entfernung vom Hubschrauber zur Bergsteigergruppe beträgt 13,75 km.
Die Zeit bis der Hubschrauber eintrifft kannst du mithilfe der angegebenen Geschwindigkeit berechnen:

$\dfrac{13,75 \text{km}}{250 \frac{\text{km}}{\text{h}}} = 0,055 \text{h}$

Rechne die Stundenangabe jetzt noch in Minuten um, indem du das Ergebnis mit 60 multiplizierst:

$t = 0,055 \cdot 60 = 3,3$ min

Der Hubschrauber braucht also 3,3 Minuten um zum Ort der Bergsteiger zu gelangen.

b) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{P}$ bestimmen

$g_1: \vec{x} = \overrightarrow{ON} + t\cdot \vec{k} = \begin{pmatrix}2\\-6\\4\end{pmatrix} + t\cdot \begin{pmatrix}-1\\0\\-2\end{pmatrix}$

$g_2: \vec{x} = \overrightarrow{O} + u\cdot \overrightarrow{m} = u\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$

Setze diese beiden Geradengleichungen nun gleich um den Schnittpunkt zu bestimmen:

$\begin{array}{rcll} \begin{pmatrix}2\\-6\\4\end{pmatrix} + t\cdot \begin{pmatrix}-1\\0\\-2\end{pmatrix}&=&u\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}& \end{array}$

Aus dieser Gleichung ergibt sich das folgende lineare Gleichungssystem welches du wieder mit dem CAS lösen kannst:

$\begin{array}{lrcccr} (1)&-0,5 \cdot u&=&2&-&t&&\\ (2)&2 \cdot u&=&-6&+&0&&\\ (3)&-u&=&4&-&2 \cdot t&&& \end{array}$

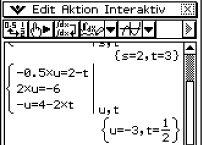Bildschirmaufnahme eines interaktiven Editortools mit mathematischen Gleichungen.

Es folgt $u=-3$ und $t=0,5$ .

Setze $u$ oder $t$ nun in die passende Gerade ein, um die Koordinaten von $P$ zu berechnen.

$P = (-3) \cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix} = \begin{pmatrix}1,5\\-6\\3\end{pmatrix}$

Die gesuchten Koordinaten sind gegeben durch $\boldsymbol{P(1,5\mid -6\mid 3)}$ .

$\blacktriangleright$ Winkel berechnen

Der gesuchte Winkel ist der Winkel zwischen den Geraden $g_1$ und $g_2$ . Den Winkel zwischen zwei Geraden berechnest du mit folgender Formel:

$\boldsymbol{\alpha = \arccos\left(\dfrac{\mid \overrightarrow{a_1} \cdot \overrightarrow{a_2}\mid}{\mid \overrightarrow{a_1}\mid \cdot \mid \overrightarrow{a_2}\mid}\right)}$

$\mid \vec{k} \cdot \overrightarrow{m}\mid$ $= \left|\begin{pmatrix}-1\\0\\-2\end{pmatrix} \cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}\right|$ $= \mid (-1)\cdot (-0,5) + 0 \cdot 2 + (-2) \cdot (-1)\mid = 2,5$
$\mid \vec{k}\mid$ $= \left|\begin{pmatrix}-1\\0\\-2\end{pmatrix}\right|$ $= \sqrt{(-1)^2 + 0^2 + (-2)^2}$ $= \sqrt{5}$
$\mid \overrightarrow{m}\mid$ $= \left|\begin{pmatrix}-0,5\\2\\-1\end{pmatrix}\right|$ $= \sqrt{(-0,5)^2 + 2^2 + (-1)^2}$ $= \sqrt{5,25}$

Für den Winkel ergibt sich dann:

$\alpha = \arccos\left(\dfrac{\mid \vec{k} \cdot \overrightarrow{m}\mid}{\mid \vec{k}\mid \cdot \mid \overrightarrow{m}\mid}\right)$ $= \dfrac{2,5}{\sqrt{5}\cdot \sqrt{5,25}}= 60,8\;^{\circ}$

Der Hubschrauber ändert seinen Kurs im Punkt $P$ um $\boldsymbol{60,8\;^{\circ}}$ .

c) $\blacktriangleright$ Den Wert $\boldsymbol{z}$ bestimmen

Der Kurs in $P_z(1,5\mid-6\mid z)$ soll sich unter einem Winkel von $90\;^{\circ}$ ändern. Du sollst nun alle Werte für $z$ bestimmen.

Die beiden Richtungen sind gegeben durch:

$\overrightarrow{NP_z} = \begin{pmatrix}1,5\\-6\\z\end{pmatrix} - \begin{pmatrix}2\\-6\\4\end{pmatrix}$ $= \begin{pmatrix}-0,5\\0\\z-4\end{pmatrix}$

$\overrightarrow{P_z O} = \begin{pmatrix}0\\0\\0\end{pmatrix}-\begin{pmatrix}1,5\\-6\\z\end{pmatrix}$ $= \begin{pmatrix}-1,5\\6\\-z\end{pmatrix}$

Berechne nun das Skalarprodukt der beiden Richtungen in Abhängigkeit von $z$ :

Dieses Skalarprodukt soll 0 sein, berechne also die Nullstellen der quadratischen Funktion mit dem solve-Befehl deines Taschenrechners.

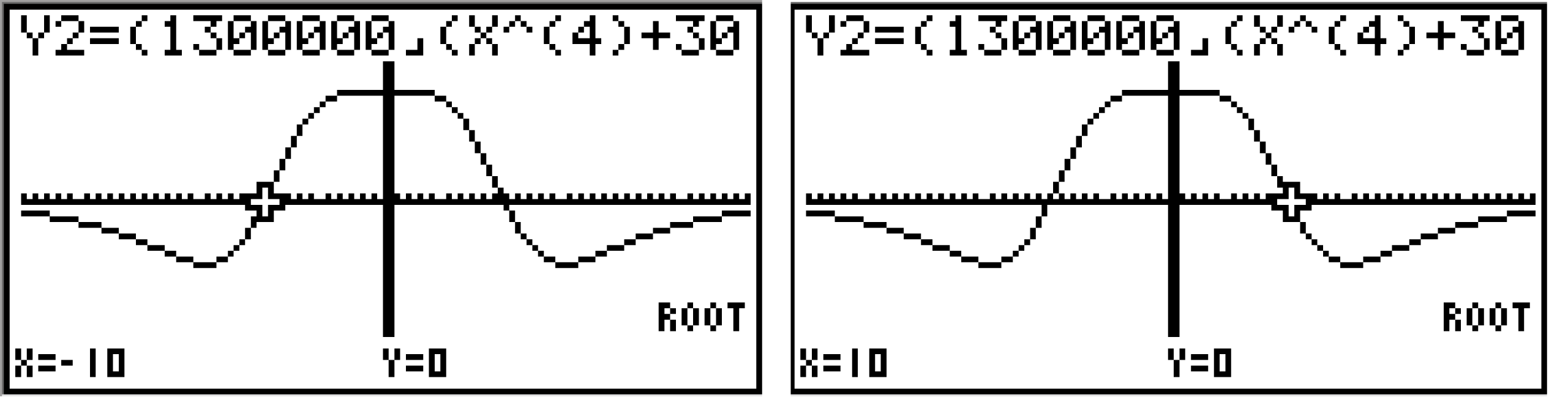Diagramm mit mathematischen Funktionen, das zwei Kurven und ihre Schnittpunkte darstellt.

Du erhältst zwei Nullstellen $z_1 = -0,179$ und $z_2 = 4,179$ . Es existieren somit zwei passende Werte für $\boldsymbol{z}$ .