Aufgabe 2B
In der Zeitung „DIE ZEIT“ vom 21.03.2013 war zum Intelligenzquotienten (IQ) Folgendes zu lesen:
 , die jeder zufällig ausgewählten Person ihren IQ zuordnet, wird als normalverteilt angenommen.
, die jeder zufällig ausgewählten Person ihren IQ zuordnet, wird als normalverteilt angenommen.
„Der IQ gibt an, wie intelligent eine Testperson im Vergleich zu anderen Gleichaltrigen aus derselben Bevölkerung ist. Intelligenzvergleiche zwischen sehr unterschiedlichen Gruppen, etwa Völkern, verbieten sich, weil Intelligenztests kulturell geprägt sind. Mit einem IQ von 100 verfügt man über durchschnittliche Intelligenz [...]. Zwei Drittel der Bevölkerung haben einen IQ zwischen 85 und 115. Rund 17 Prozent können mit einem IQ von mehr als 115 als überdurchschnittlich intelligent gelten, und 2 Prozent mit einem IQ von mehr als 130 als hochbegabt.“
Die Zufallsgröße
a) Erläutern Sie, dass unter diesen Voraussetzungen der Erwartungswert  und die Standardabweichung
und die Standardabweichung  der Zufallsgröße
der Zufallsgröße  mit den Aussagen des obigen Textes näherungsweise ermittelt werden können.
Berechnen Sie mithilfe der Zufallsgröße
mit den Aussagen des obigen Textes näherungsweise ermittelt werden können.
Berechnen Sie mithilfe der Zufallsgröße  die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist.
Berechnen Sie mithilfe der Zufallsgröße
die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist.
Berechnen Sie mithilfe der Zufallsgröße  den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist.
den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist.
(9P)
b) Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von etwa 2,3 % hochbegabt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich unter 120 zufällig ausgewählten Personen mindestens eine hochbegabte Person befindet.
Der Wahrscheinlichkeitswert von 2,3 % für das Vorhandensein einer Hochbegabung wird angezweifelt. Es wird deshalb eine Stichprobe von 450 zufällig ausgewählten Personen untersucht. Die Untersuchung ergibt, dass sich in der Stichprobe 16 hochbegabte Personen befinden.
Entscheiden Sie mithilfe eines Vertrauensintervalls, ob man bei einer Vertrauenswahrscheinlichkeit von  davon ausgehen kann, dass die Zweifel berechtigt sind.
davon ausgehen kann, dass die Zweifel berechtigt sind.
(8P)
c) Für die obige normalverteilte Zufallsgröße  ist
ist  mit
mit  die Dichtefunktion.
Bestimmen Sie in den beiden Gleichungen
die Dichtefunktion.
Bestimmen Sie in den beiden Gleichungen  und
und  die Werte für
die Werte für  und
und  .
Es soll gelten:
.
Es soll gelten:  Begründen Sie, dass daraus
Begründen Sie, dass daraus  folgt.
folgt.
(7P)
(24P)
a)  Erwartungswert und Varianz erläutern
Du findest im Text die Aussage, dass ein IQ von 100 eine durchschnittliche Intelligenz bedeutet, daraus kannst du folgern, dass der Erwartungswert
Erwartungswert und Varianz erläutern
Du findest im Text die Aussage, dass ein IQ von 100 eine durchschnittliche Intelligenz bedeutet, daraus kannst du folgern, dass der Erwartungswert  entspricht. Wenn du etwas grob rundest sind
entspricht. Wenn du etwas grob rundest sind  , das ist gerade die Wahrscheinlichkeit des
, das ist gerade die Wahrscheinlichkeit des  -Bereichs von
-Bereichs von  . Die
. Die  sind der Bereich von 85 bis 115. Daraus folgt eine Standardabweichung von
sind der Bereich von 85 bis 115. Daraus folgt eine Standardabweichung von  .
.
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist. Die Zufallsvariable
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist. Die Zufallsvariable  ist normalverteilt, du kannst also die Tabelle der Standardnormalverteilung nutzen. Du sollst also berechnen:
ist normalverteilt, du kannst also die Tabelle der Standardnormalverteilung nutzen. Du sollst also berechnen:
 Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist, beträgt
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist, beträgt  .
Berechne den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist. Du sollst also berechnen:
.
Berechne den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist. Du sollst also berechnen:
 Der Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105, beträgt
Der Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105, beträgt  .
.
b)  Wahrscheinlichkeit bestimmen
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von etwa 2,3 % hochbegabt. Du sollst die Wahrscheinlichkeit berechnen, dass sich unter 120 zufällig ausgewählten Personen mindestens eine hochbegabte Person befindet. Sei
Wahrscheinlichkeit bestimmen
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von etwa 2,3 % hochbegabt. Du sollst die Wahrscheinlichkeit berechnen, dass sich unter 120 zufällig ausgewählten Personen mindestens eine hochbegabte Person befindet. Sei  die Anzahl der Hochbegabten, diese ist binomialverteilt mit
die Anzahl der Hochbegabten, diese ist binomialverteilt mit  und
und  , da hier nur zwei Ausprägungen betrachtet werden: „hochbegabt“ und „nicht hochbegabt“. Zudem ist für jede Person die Wahrscheinlichkeit gleich, dass diese hochbegabt ist. Die gesuchte Wahrscheinlichkeit berechnest du wie folgt:
, da hier nur zwei Ausprägungen betrachtet werden: „hochbegabt“ und „nicht hochbegabt“. Zudem ist für jede Person die Wahrscheinlichkeit gleich, dass diese hochbegabt ist. Die gesuchte Wahrscheinlichkeit berechnest du wie folgt:
 Unter 120 zufällig ausgewählten Personen befindet sich mit einer Wahrscheinlichkeit von ca.
Unter 120 zufällig ausgewählten Personen befindet sich mit einer Wahrscheinlichkeit von ca.  mindestens eine hochbegabte Person.
mindestens eine hochbegabte Person.
 Vertrauensintervall bestimmen
Du sollst nun ein Vertrauensintervall
Vertrauensintervall bestimmen
Du sollst nun ein Vertrauensintervall  für den Anteil der Hochbegabten bestimmen.
Sei
für den Anteil der Hochbegabten bestimmen.
Sei  zunächst jene Zufallsgröße, welche die Anzahl der Hochbegabten in der Stichprobe angibt.
zunächst jene Zufallsgröße, welche die Anzahl der Hochbegabten in der Stichprobe angibt.  kann näherungsweise als binomialverteilte Zufallsgröße angenommen werden mit
kann näherungsweise als binomialverteilte Zufallsgröße angenommen werden mit  und
und  unbekannt. Einen ersten Schätzwert für
unbekannt. Einen ersten Schätzwert für  kannst du über die Angabe ermitteln, dass 16 von 450 hochbegabt sind:
kannst du über die Angabe ermitteln, dass 16 von 450 hochbegabt sind:  .
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil
.
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil  der Hochbegabten mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die
der Hochbegabten mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die  -Regeln. Diese dürfen angewandt werden, wenn das Laplace-Kriterium
-Regeln. Diese dürfen angewandt werden, wenn das Laplace-Kriterium  erfüllt ist. Tatsächlich ergibt sich z.B. mit dem Schätzwert
erfüllt ist. Tatsächlich ergibt sich z.B. mit dem Schätzwert  für
für  die Standardabweichung
die Standardabweichung
 .
Selbstverständlich kann dies nur als Näherung gesehen werden. Tendenziell kann aber davon ausgegangen werden, dass die Bedingung
.
Selbstverständlich kann dies nur als Näherung gesehen werden. Tendenziell kann aber davon ausgegangen werden, dass die Bedingung  erfüllt ist.
Du kannst also so vorgehen:
erfüllt ist.
Du kannst also so vorgehen:
 -Regel auswählen
Du findest die Regel
-Regel auswählen
Du findest die Regel
 2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über
2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über  trifft. Du kennst bereits:
trifft. Du kennst bereits:
![\(\begin{array}[t]{rcccll}
\mu-1,96\sigma&\leq &Y&\leq&\mu+1,96\sigma&\\
n\cdot p-1,96\sigma&\leq &Y&\leq&n\cdot p+1,96\sigma&\\
n\cdot p-1,96\cdot\sqrt{n\cdot p\cdot (1-p)}&\leq &Y&\leq&n\cdot p+1,96\sqrt{n\cdot p\cdot (1-p)}&\\
p-1,96\cdot\sqrt{\dfrac{p\cdot (1-p)}{n}}&\leq &\dfrac{Y}{n}&\leq&p+1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}&\\
-1,96\cdot\sqrt{\dfrac{p\cdot (1-p)}{n}}&\leq &\dfrac{Y}{n}-p&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}\\
\left|\dfrac{Y}{n}-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}&&&\\
\left|0,036-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{450}}
\end{array}\)](https://www.schullv.de/resources/formulas/45fce54f2546d69c2dbce6fa0fc35f0920c13df177638395e5b716c9d96fbfc4_light.svg) 3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach
3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach  auflösen.
auflösen.
![\(\begin{array}[t]{rcll}
\left|0,036-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{450}}&\\
(0,036-p)^2&\leq&(1,96)^2\cdot\dfrac{p\cdot(1-p)}{450}\\
0,036^2-2\cdot0,036\cdot p+p^2&\leq&\dfrac{3,8416}{450}\cdot p\cdot(1-p)\\
0,036^2-2\cdot0,036\cdot p+p^2&\leq&\dfrac{3,8416}{450}p-\dfrac{3,8416}{450}p^2&\\
p^2+\dfrac{3,8416}{450}p^2-2\cdot0,036\cdot p-\dfrac{3,8416}{450}p+0,036^2&\leq&0
\end{array}\)](https://www.schullv.de/resources/formulas/d16f5001df4d943a079ed1772cc0ef56434dbe71eb671bddd1d132142189bf63_light.svg) Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm
Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm  einer Funktion
einer Funktion  auf. Der Graph von
auf. Der Graph von  ist eine nach oben geöffnete Parabel.
Gesucht ist der Bereich, in welchem
ist eine nach oben geöffnete Parabel.
Gesucht ist der Bereich, in welchem  negative Funktionswerte annimmt, d.h. der Bereich, in dem die Parabel unterhalb der
negative Funktionswerte annimmt, d.h. der Bereich, in dem die Parabel unterhalb der  -Achse verläuft. Du kannst diese Ungleichung mit dem solve-Befehl deines Taschenrechners lösen:
-Achse verläuft. Du kannst diese Ungleichung mit dem solve-Befehl deines Taschenrechners lösen:
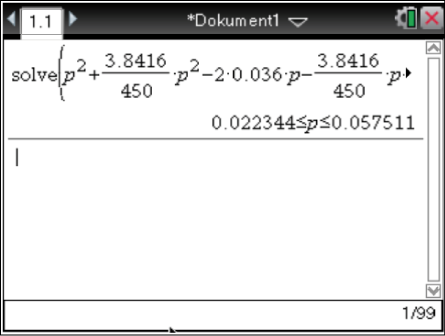 Der Taschenrechner liefert den Bereich
Der Taschenrechner liefert den Bereich  .
Damit folgt: der tatsächliche Anteil
.
Damit folgt: der tatsächliche Anteil  der Hochbegabten liegt mit einer Wahrscheinlichkeit von 95 % im Intervall
der Hochbegabten liegt mit einer Wahrscheinlichkeit von 95 % im Intervall ![\(\boldsymbol{[0,022\,;\,0,058]}\)](https://www.schullv.de/resources/formulas/7ddde72326e0ecee3f2f666a094fd62c13642dabc446252a05360cfec4fb0c77_light.svg) . Da dieses Intervall den Wert
. Da dieses Intervall den Wert  überdeckt, kann man von dieser Stichprobe ausgehend nicht folgern, dass die Zweifel berechtigt sind.
überdeckt, kann man von dieser Stichprobe ausgehend nicht folgern, dass die Zweifel berechtigt sind.
- Wähle die
-Regel, welche eine Aussage über ein 95 %-Konfidenzintervall um den Erwartungswert
trifft.
- Bedenke:
. Forme den Ausdruck in der
-Regel also so um, dass er eine Aussage über
trifft. Hieraus ergibt sich:
.
- Löse die Ungleichung nach
auf und berechne so die Grenzen des Intervalls.
- die relative Häufigkeit

c)  Werte für
Werte für  und
und  bestimmen
Du sollst die Werte für
bestimmen
Du sollst die Werte für  und
und  bestimmen, nutze dafür deinen Taschenrechner. Die oben angegebene Normalverteilung hat den Mittelwert
bestimmen, nutze dafür deinen Taschenrechner. Die oben angegebene Normalverteilung hat den Mittelwert  und die Standardabweichung
und die Standardabweichung  .
menu:
.
menu:  5:
5:  5:
5:  3:
Die oben angegebene Normalverteilung hat den Mittelwert
3:
Die oben angegebene Normalverteilung hat den Mittelwert  und die Standardabweichung
und die Standardabweichung  .
.
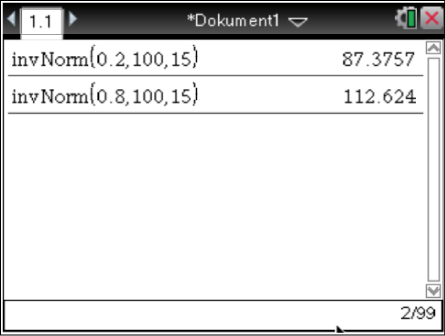 Du erhältst folgende Werte
Du erhältst folgende Werte  und
und  .
.
 Begründe die Aussage
Es soll gelten:
Begründe die Aussage
Es soll gelten:
 Du sollst begründen, warum daraus
Du sollst begründen, warum daraus  folgt.
Die Integraldarstellung lässt sich umschreiben in:
folgt.
Die Integraldarstellung lässt sich umschreiben in:
 Die Dichtefunktion
Die Dichtefunktion  ist symmetrisch zu
ist symmetrisch zu  , deshalb ist der Mittelwert von
, deshalb ist der Mittelwert von  und
und  gerade
gerade  und es gilt
und es gilt  .
.

a)  Erwartungswert und Varianz erläutern
Du findest im Text die Aussage, dass ein IQ von 100 eine durchschnittliche Intelligenz bedeutet, daraus kannst du folgern, dass der Erwartungswert
Erwartungswert und Varianz erläutern
Du findest im Text die Aussage, dass ein IQ von 100 eine durchschnittliche Intelligenz bedeutet, daraus kannst du folgern, dass der Erwartungswert  entspricht. Wenn du etwas grob rundest sind
entspricht. Wenn du etwas grob rundest sind  , das ist gerade die Wahrscheinlichkeit des
, das ist gerade die Wahrscheinlichkeit des  -Bereichs von
-Bereichs von  . Die
. Die  sind der Bereich von 85 bis 115. Daraus folgt eine Standardabweichung von
sind der Bereich von 85 bis 115. Daraus folgt eine Standardabweichung von  .
.
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist. Die Zufallsvariable
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist. Die Zufallsvariable  ist normalverteilt, du kannst also die Tabelle der Standardnormalverteilung nutzen. Du sollst also berechnen:
ist normalverteilt, du kannst also die Tabelle der Standardnormalverteilung nutzen. Du sollst also berechnen:
 Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist, beträgt
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person einen IQ hat, der größer als 115 ist, beträgt  .
Berechne den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist. Du sollst also berechnen:
.
Berechne den Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105 ist. Du sollst also berechnen:
 Der Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105, beträgt
Der Anteil der Bevölkerung mit einem IQ, der größer als 95 und kleiner als 105, beträgt  .
.
b)  Wahrscheinlichkeit bestimmen
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von etwa 2,3 % hochbegabt. Du sollst die Wahrscheinlichkeit berechnen, dass sich unter 120 zufällig ausgewählten Personen mindestens eine hochbegabte Person befindet. Sei
Wahrscheinlichkeit bestimmen
Eine zufällig ausgewählte Person ist mit einer Wahrscheinlichkeit von etwa 2,3 % hochbegabt. Du sollst die Wahrscheinlichkeit berechnen, dass sich unter 120 zufällig ausgewählten Personen mindestens eine hochbegabte Person befindet. Sei  die Anzahl der Hochbegabten, diese ist binomialverteilt mit
die Anzahl der Hochbegabten, diese ist binomialverteilt mit  und
und  , da hier nur zwei Ausprägungen betrachtet werden: „hochbegabt“ und „nicht hochbegabt“. Zudem ist für jede Person die Wahrscheinlichkeit gleich, dass diese hochbegabt ist. Die gesuchte Wahrscheinlichkeit berechnest du wie folgt:
, da hier nur zwei Ausprägungen betrachtet werden: „hochbegabt“ und „nicht hochbegabt“. Zudem ist für jede Person die Wahrscheinlichkeit gleich, dass diese hochbegabt ist. Die gesuchte Wahrscheinlichkeit berechnest du wie folgt:
 Unter 120 zufällig ausgewählten Personen befindet sich mit einer Wahrscheinlichkeit von ca.
Unter 120 zufällig ausgewählten Personen befindet sich mit einer Wahrscheinlichkeit von ca.  mindestens eine hochbegabte Person.
mindestens eine hochbegabte Person.
 Vertrauensintervall bestimmen
Du sollst nun ein Vertrauensintervall
Vertrauensintervall bestimmen
Du sollst nun ein Vertrauensintervall  für den Anteil der Hochbegabten bestimmen.
Sei
für den Anteil der Hochbegabten bestimmen.
Sei  zunächst jene Zufallsgröße, welche die Anzahl der Hochbegabten in der Stichprobe angibt.
zunächst jene Zufallsgröße, welche die Anzahl der Hochbegabten in der Stichprobe angibt.  kann näherungsweise als binomialverteilte Zufallsgröße angenommen werden mit
kann näherungsweise als binomialverteilte Zufallsgröße angenommen werden mit  und
und  unbekannt. Einen ersten Schätzwert für
unbekannt. Einen ersten Schätzwert für  kannst du über die Angabe ermitteln, dass 16 von 450 hochbegabt sind:
kannst du über die Angabe ermitteln, dass 16 von 450 hochbegabt sind:  .
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil
.
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil  der Hochbegabten mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die
der Hochbegabten mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die  -Regeln. Diese dürfen angewandt werden, wenn das Laplace-Kriterium
-Regeln. Diese dürfen angewandt werden, wenn das Laplace-Kriterium  erfüllt ist. Tatsächlich ergibt sich z.B. mit dem Schätzwert
erfüllt ist. Tatsächlich ergibt sich z.B. mit dem Schätzwert  für
für  die Standardabweichung
die Standardabweichung
 .
Selbstverständlich kann dies nur als Näherung gesehen werden. Tendenziell kann aber davon ausgegangen werden, dass die Bedingung
.
Selbstverständlich kann dies nur als Näherung gesehen werden. Tendenziell kann aber davon ausgegangen werden, dass die Bedingung  erfüllt ist.
Du kannst also so vorgehen:
erfüllt ist.
Du kannst also so vorgehen:
 -Regel auswählen
Du findest die Regel
-Regel auswählen
Du findest die Regel
 2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über
2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über  trifft. Du kennst bereits:
trifft. Du kennst bereits:
![\(\begin{array}[t]{rcccll}
\mu-1,96\sigma&\leq &Y&\leq&\mu+1,96\sigma&\\
n\cdot p-1,96\sigma&\leq &Y&\leq&n\cdot p+1,96\sigma&\\
n\cdot p-1,96\cdot\sqrt{n\cdot p\cdot (1-p)}&\leq &Y&\leq&n\cdot p+1,96\sqrt{n\cdot p\cdot (1-p)}&\\
p-1,96\cdot\sqrt{\dfrac{p\cdot (1-p)}{n}}&\leq &\dfrac{Y}{n}&\leq&p+1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}&\\
-1,96\cdot\sqrt{\dfrac{p\cdot (1-p)}{n}}&\leq &\dfrac{Y}{n}-p&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}\\
\left|\dfrac{Y}{n}-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{n}}&&&\\
\left|0,036-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{450}}
\end{array}\)](https://www.schullv.de/resources/formulas/45fce54f2546d69c2dbce6fa0fc35f0920c13df177638395e5b716c9d96fbfc4_light.svg) 3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach
3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach  auflösen.
auflösen.
![\(\begin{array}[t]{rcll}
\left|0,036-p\right|&\leq&1,96\sqrt{\dfrac{p\cdot (1-p)}{450}}&\\
(0,036-p)^2&\leq&(1,96)^2\cdot\dfrac{p\cdot(1-p)}{450}\\
0,036^2-2\cdot0,036\cdot p+p^2&\leq&\dfrac{3,8416}{450}\cdot p\cdot(1-p)\\
0,036^2-2\cdot0,036\cdot p+p^2&\leq&\dfrac{3,8416}{450}p-\dfrac{3,8416}{450}p^2&\\
p^2+\dfrac{3,8416}{450}p^2-2\cdot0,036\cdot p-\dfrac{3,8416}{450}p+0,036^2&\leq&0
\end{array}\)](https://www.schullv.de/resources/formulas/d16f5001df4d943a079ed1772cc0ef56434dbe71eb671bddd1d132142189bf63_light.svg) Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm
Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm  einer Funktion
einer Funktion  auf. Der Graph von
auf. Der Graph von  ist eine nach oben geöffnete Parabel.
Gesucht ist der Bereich, in welchem
ist eine nach oben geöffnete Parabel.
Gesucht ist der Bereich, in welchem  negative Funktionswerte annimmt, d.h. der Bereich, in dem die Parabel unterhalb der
negative Funktionswerte annimmt, d.h. der Bereich, in dem die Parabel unterhalb der  -Achse verläuft. Du kannst diese Ungleichung mit dem solve-Befehl deines Taschenrechners lösen:
-Achse verläuft. Du kannst diese Ungleichung mit dem solve-Befehl deines Taschenrechners lösen:
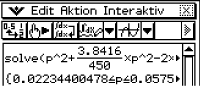 Der Taschenrechner liefert den Bereich
Der Taschenrechner liefert den Bereich  .
Damit folgt: der tatsächliche Anteil
.
Damit folgt: der tatsächliche Anteil  der Hochbegabten liegt mit einer Wahrscheinlichkeit von 95 % im Intervall
der Hochbegabten liegt mit einer Wahrscheinlichkeit von 95 % im Intervall ![\(\boldsymbol{[0,022\,;\,0,058]}\)](https://www.schullv.de/resources/formulas/7ddde72326e0ecee3f2f666a094fd62c13642dabc446252a05360cfec4fb0c77_light.svg) . Da dieses Intervall den Wert
. Da dieses Intervall den Wert  überdeckt, kann man von dieser Stichprobe ausgehend nicht folgern, dass die Zweifel berechtigt sind.
überdeckt, kann man von dieser Stichprobe ausgehend nicht folgern, dass die Zweifel berechtigt sind.
- Wähle die
-Regel, welche eine Aussage über ein 95 %-Konfidenzintervall um den Erwartungswert
trifft.
- Bedenke:
. Forme den Ausdruck in der
-Regel also so um, dass er eine Aussage über
trifft. Hieraus ergibt sich:
.
- Löse die Ungleichung nach
auf und berechne so die Grenzen des Intervalls.
- die relative Häufigkeit

c)  Werte für
Werte für  und
und  bestimmen
Du sollst die Werte für
bestimmen
Du sollst die Werte für  und
und  bestimmen, nutze dafür das Statistik-Menü deines Taschenrechners. Die oben angegebene Normalverteilung hat den Mittelwert
bestimmen, nutze dafür das Statistik-Menü deines Taschenrechners. Die oben angegebene Normalverteilung hat den Mittelwert  und die Standardabweichung
und die Standardabweichung  .
CALC
.
CALC  Verteilung
Verteilung  Typ: Inv. Verteilung
Typ: Inv. Verteilung  Quantile Normalvert.
Die oben angegebene Normalverteilung hat den Mittelwert
Quantile Normalvert.
Die oben angegebene Normalverteilung hat den Mittelwert  und die Standardabweichung
und die Standardabweichung  .
.
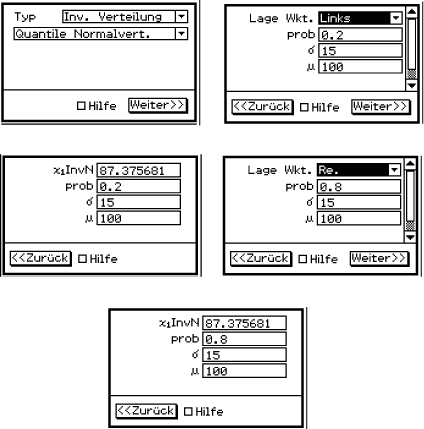 Du erhältst folgende Werte
Du erhältst folgende Werte  und
und  .
.
 Begründe die Aussage
Es soll gelten:
Begründe die Aussage
Es soll gelten:
 Du sollst begründen, warum daraus
Du sollst begründen, warum daraus  folgt.
Die Integraldarstellung lässt sich umschreiben in:
folgt.
Die Integraldarstellung lässt sich umschreiben in:
 Die Dichtefunktion
Die Dichtefunktion  ist symmetrisch zu
ist symmetrisch zu  , deshalb ist der Mittelwert von
, deshalb ist der Mittelwert von  und
und  gerade
gerade  und es gilt
und es gilt  .
.
