SchulLV

Gegeben ist die in $\mathbb{R} \backslash\{-2\}$ definierte Funktion $f: x \mapsto \frac{x^2-9}{x+2}.$

a)

Gib die Nullstellen von $f$ sowie die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse an.

(2 BE)

b)

Gib das Verhalten von $f$ für $x \rightarrow-\infty$ sowie für $x \rightarrow+\infty$ an.

(2 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $g$ mit $g(x)=x^3+x^2.$ Abbildung 1 zeigt den Graphen von $g.$

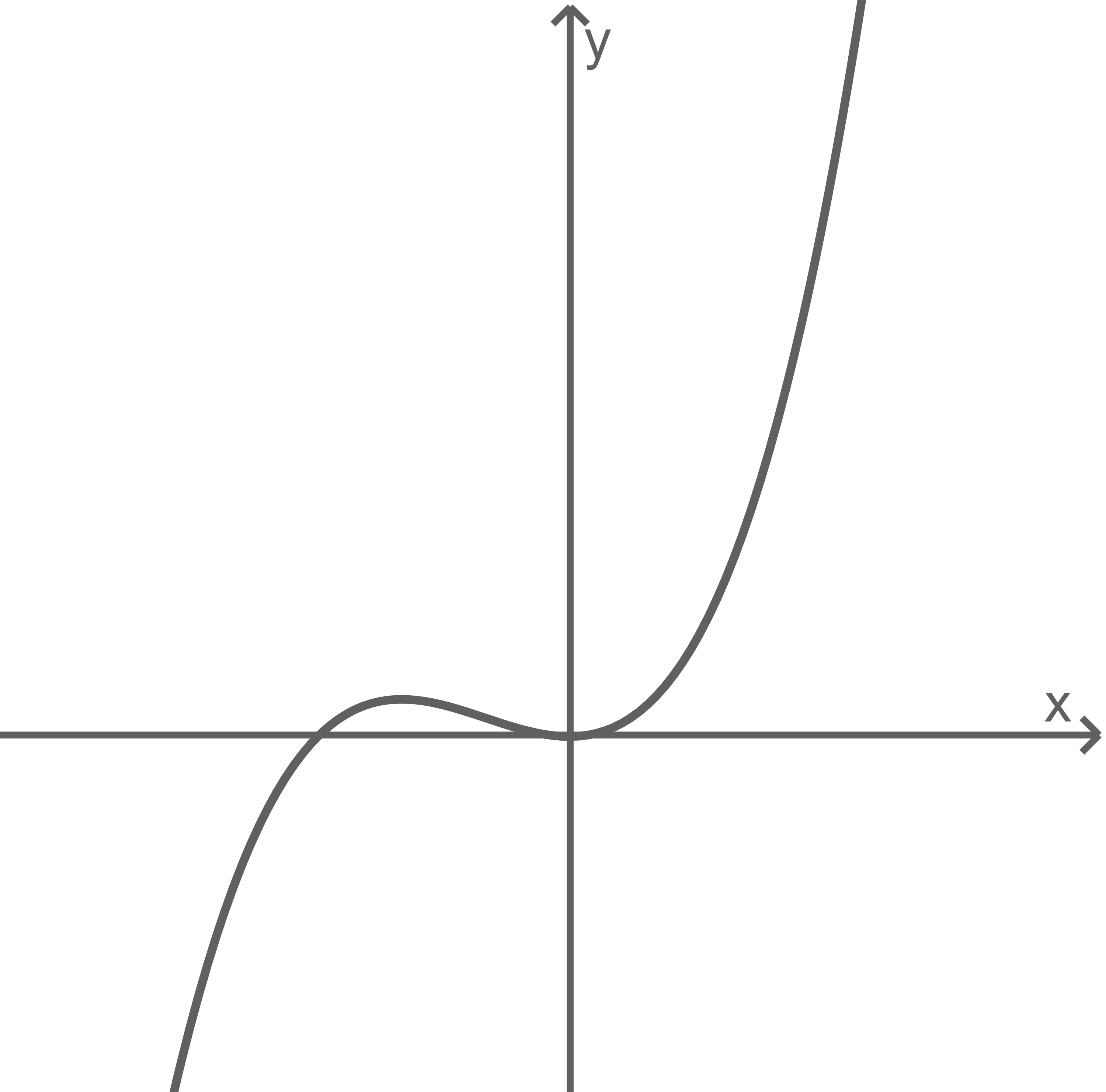
Abb. 1

a)

Gib einen Term der ersten Ableitungsfunktion von $g$ an.

(1 BE)

b)

Berechne den Inhalt der Fläche, die der Graph von $g$ mit der $x$ -Achse einschließt.

(4 BE)

Gegeben ist die in $[-3 ;+\infty[$ definierte Funktion $h: x \mapsto \sqrt{x+3}-2.$

a)

Beschreibe, wie der Graph von $h$ aus dem Graphen der in $\mathbb{R}_0^{+}$ definierten Funktion $w: x \mapsto \sqrt{x}$ hervorgeht.

(2 BE)

b)

Begründe, dass $h$ umkehrbar ist, und beschreibe, wie der Graph der Umkehrfunktion $h^{-1}$ von $h$ aus dem Graphen von $h$ hervorgeht. Gib den Definitions- und den Wertebereich von $h^{-1}$ an.

(4 BE)

Gegeben ist für jede positive reelle Zahl $a$ die in $\mathbb{R}$ definierte Funktion $f_a$ mit $f_a(x)=ax^2.$

Abbildung 2 zeigt den Graphen von $f_{\frac{1}{2}}$ sowie die Tangente $t$ an den Graphen von $f_{\frac{1}{2}}$ im Punkt $\left(4 \;\left\lvert\; f_{\frac{1}{2}}(4)\right.\right).$

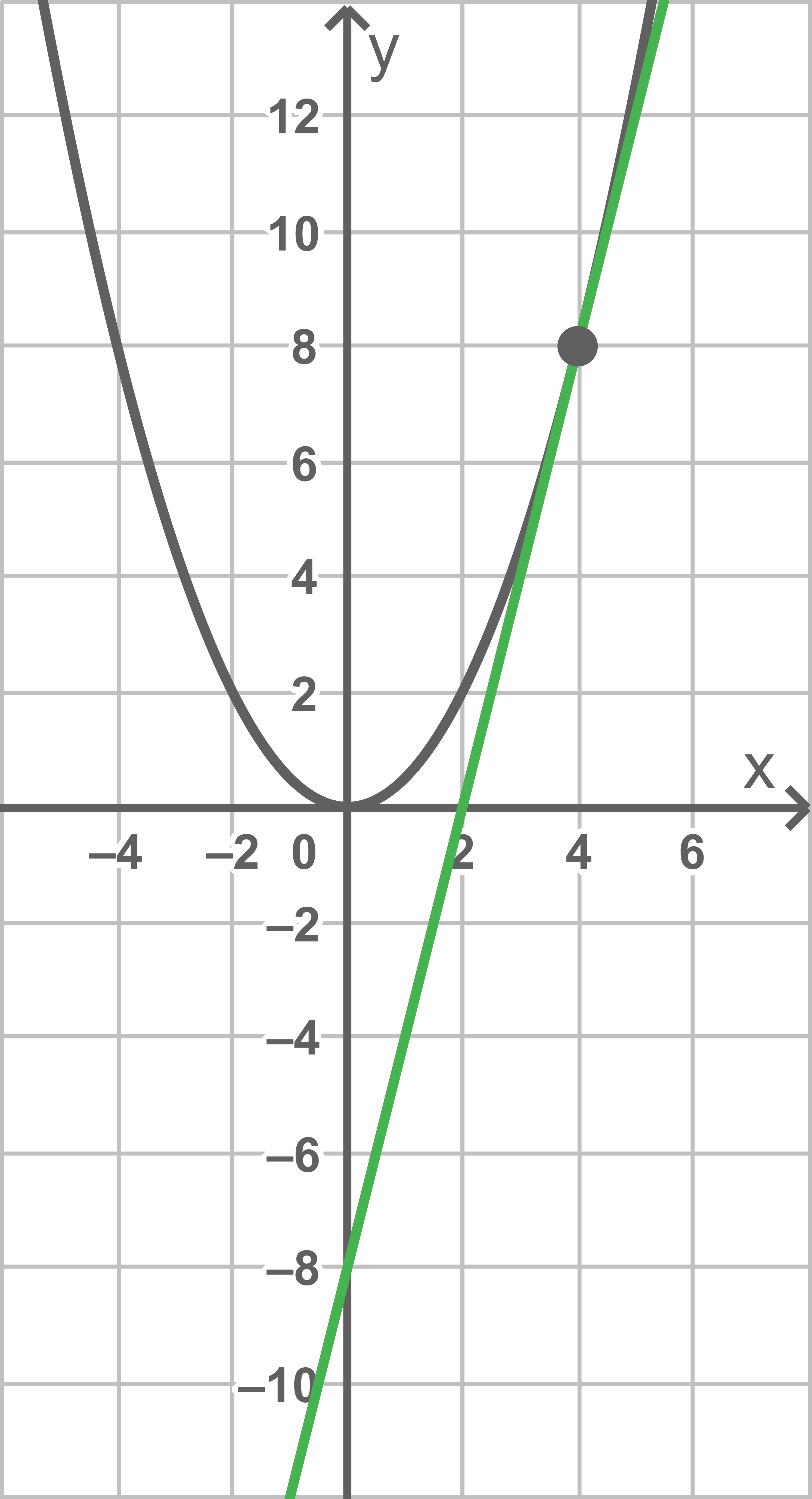
Abb. 1

a)

Gib anhand von Abbildung 2 eine Gleichung der Tangente $t$ an.

(1 BE)

b)

Weise nach, dass für jeden Wert $u \in \mathbb{R}$ die Tangente an den Graphen von $f_a$ im Punkt $\left(u \mid f_a(u)\right)$ die $y$ -Achse im Punkt $\left(0 \mid-f_a(u)\right)$ schneidet.

(4 BE)

(20 BE)