Stochastik Prüfungsteil B

Aufgabengruppe 1

1 Der Marketingchef einer Handelskette plant eine Werbeaktion, bei der ein Kunde die Höhe des Rabatts bei seinem Einkauf durch zweimaliges Drehen an einem Glücksrad selbst bestimmen kann. Das Glücksrad hat zwei Sektoren, die mit den Zahlen $5$ bzw. $2$ beschriftet sind (vgl. Abbildung).

Kreisdiagramm mit den Zahlen 2 und 5, Pfeil zeigt auf den Abschnitt mit der Zahl 5.

$\;\;$ Der Rabatt in Prozent errechnet sich als Produkt der beiden Zahlen, die der Kunde bei zweimaligem Drehen am Glücksrad erzielt.
Die Zufallsgröße $X$ beschreibt die Höhe dieses Rabatts in Prozent, kann also die Werte $4$ , $10$ oder $25$ annehmen. Die Zahl $5$ wird beim Drehen des Glücksrads mit der Wahrscheinlichkeit $p$ erzielt.
Vereinfachend soll davon ausgegangen werden, dass jeder Kunde genau einen Einkauf tätigt und auch tatsächlich am Glücksrad dreht.

a) Ermittle mithilfe eines Baumdiagramms die Wahrscheinlichkeit dafür, dass ein Kunde bei seinem Einkauf einen Rabatt von $10\,\%$ erhält. (Ergebnis: $2p-2p^2$ )

(3P)

b) Zeige, dass für den Erwartungswert $E(X)$ der Zufallsgröße $X$ gilt:
$E(X)=9p^2+12p+4$ .

(2P)

c) Die Geschäftsführung will im Mittel für einen Einkauf einen Rabatt von $16\,\%$ gewähren. Berechne für diese Vorgabe den zugehörigen Mittelpunktswinkel des Sektors mit der Zahl $5$ .

(3P)

$\;\;$ Die Wahrscheinlichkeit dass ein Kunde bei seinem Einkauf den niedrigsten Rabatt erhält, beträgt $\frac{1}{9}$ .

d) Bestimme, wie viele Kunden mindestens an dem Glücksrad drehen müssen, damit mit einer Wahrscheinlichkeit von mehr als $99\,\%$ mindestens einer der Kunden den niedrigsten Rabatt erhält.

(3P)

e) Es drehen $180$ Kunden am Glücksrad. Berechne, mit welcher Wahrscheinlichkeit mindestens $10$ und höchstens $25$ dieser Kunden den niedrigsten Rabatt für ihren Einkauf erhalten.

(2P)

2 Eine der Filialen der Handelskette befindet sich in einem Einkaufszentrum, das zu Werbezwecken die Erstellung einer Smartphone-App in Auftrag geben will. Diese App soll die Kunden beim Betreten des Einkaufszentrums über aktuelle Angebote und Rabattaktionen der beteiligten Geschäfte informieren. Da dies mit Kosten verbunden ist, will der Finanzchef der Handelskette einer Beteiligung an der App nur zustimmen, wenn mindestens $15\,\%$ der Kunden der Filiale bereit sind, diese App zu nutzen. Der Marketingchef warnt jedoch davor, auf eine Beteiligung an der App zu verzichten, da dies zu einem Imageverlust führen könnte.
Um zu einer Entscheidung zu gelangen, will die Geschäftsführung der Handelskette eine der beiden folgenden Nullhypothesen auf der Basis einer Befragung von $200$ Kunden auf einem Signifikanzniveau von $10\,\%$ testen:

I $\;\;\;$ „Weniger als $15\,\%$ der Kunden sind bereit, die App zu nutzen.“
II $\;\;$ „Mindestens $15\,\%$ der Kunden sind bereit, die App zu nutzen.“

a) Nach Abwägung der möglichen Folgen, die der Finanzchef und der Marketingchef aufgezeigt haben, wählt die Geschäftsführung für den Test die Nullhypothese II. Bestimme die zugehörige Entscheidungsregel.

(4P)

b) Entscheide, ob bei der Abwägung, die zur Wahl der Nullhypothese II führte, die Befürchtung eines Imageverlustes oder die Kostenfrage als schwerwiegender erachtet wurde. Erläutere deine Entscheidung.

(3P)

(20P)

Aufgabengruppe 2

1 Die beiden Diagramme zeigen für die Bevölkerungsgruppe der über 14-Jährigen in Deutschland Daten zur Altersstruktur und zum Besitz von Mobiltelefonen.

Diagramm mit Altersverteilung und Mobiltelefonbesitz. Oben: Altersgruppen, unten: Besitz von Mobiltelefonen.

$\;\;$ Aus den über 14-Jährigen in Deutschland wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

$\text{M}$ :   „Die Person besitzt ein Mobiltelefon.“
$\text{S}$ :    „Die Person ist 65 Jahre oder älter.“
$\text{E}$ :    „Mindestens eines der Ereignisse $\text{M}$ und $\text{S}$ tritt ein..“

a) Schraffiere in nebenstehender Abbildung die Fläche, die dem Ereignis $\overline{\text{M}}\cap\text{S}$ entspricht.

Venn-Diagramm mit den Buchstaben M und S sowie einem Omega-Symbol.

(1P)

b) Gib an, welche zwei der folgenden Mengen I bis VI jeweils das Ereignis $\text{E}$ beschreiben.

$\;\;$

I	$\text{M}\cap\text{S}$	$\qquad$	II	$\text{M}\cup\text{S}$
III	$\overline{\text{M}\cup\text{S}}$	$\qquad$	IV	$\left(\text{M}\cap\overline{\text{S}}\right)\cup\left(\overline{\text{M}}\cap\text{S}\right) \cup\left(\overline{\text{M}}\cap\overline{\text{S}}\right)$
V	$\left(\text{M}\cap\text{S}\right)\cup\left(\text{M}\cap\overline{\text{S}}\right) \cup\left(\overline{\text{M}}\cap\text{S}\right)$	$\qquad$	IV	$\overline{\text{M}\cap\text{S}}$

(2P)

c) Entscheide anhand geeigneter Terme und auf der Grundlage der vorliegenden Daten, welche der beiden folgenden Wahrscheinlichkeiten größer ist. Begründe deine Entscheidung.

$p_1$ ist die Wahrscheinlichkeit dafür, dass die ausgewählte Person ein Mobiltelefon besitzt, wenn bekannt ist, dass sie 65 Jahre oder älter ist.

$p_2$ ist die Wahrscheinlichkeit dafür, dass die ausgewählte Person 65 Jahre oder älter ist, wenn bekannt ist, dass sie ein Mobiltelefon besitzt.

(3P)

d) Erstelle zu dem beschriebenen Sachverhalt für den Fall, dass das Ereignis $\text{E}$ mit einer Wahrscheinlichkeit von $98\,\%$ eintritt, eine vollständig ausgefüllte Vierfeldertafel. Bestimme für diesen Fall die Wahrscheinlichkeit $P_S(M)$ .

(5P)

2 Zwei Drittel der Senioren in Deutschland besitzen ein Mobiltelefon. Bei einer Talkshow zum Thema „Chancen und Risiken der digitalen Welt“ sitzen 30 Senioren im Publikum.

a) Bestimme die Wahrscheinlichkeit dafür, dass unter 30 zufällig ausgewählten Senioren in Deutschland mindestens 17 und höchstens 23 ein Mobiltelefon besitzen.

(2P)

b) Von den 30 Senioren im Publikum besitzen 24 ein Mobiltelefon. Im Verlauf der Sendung werden drei der Senioren aus dem Publikum zufällig ausgewählt und nach ihrer Meinung befragt. Bestimme die Wahrscheinlichkeit dafür, dass genau zwei dieser drei Senioren ein Mobiltelefon besitzen.

(3P)

3 Eine Handelskette hat noch zahlreiche Smartphones des Modells Y3 auf Lager, als der Hersteller das Nachfolgemodell Y4 auf den Markt bringt. Der Einkaufspreis für das neue Y4 beträgt $300$ €, während die Handelskette für das Vorgängermodell Y3 im Einkauf nur $250$ € bezahlen musste. Um die Lagerbestände noch zu verkaufen, bietet die Handelskette ab dem Verkaufsstart des Y4 die Smartphones des Typs Y3 für je $199$ € an.
Aufgrund früherer Erfahrungen geht die Handelskette davon aus, dass von den verkauften Smartphones der Modelle Y3 und Y4 trotz des Preisnachlasses nur $26\,\%$ vom Typ Y3 sein werden. Berechne unter dieser Voraussetzung, zu welchem Preis die Handelskette das Y4 anbieten muss, damit sie voraussichtlich pro verkauftem Smartphone der Modelle Y3 und Y4 im Mittel $97$ € mehr erhält, als sie beim Einkauf dafür zahlen musste.

(4P)

(20P)

Aufgabengruppe 1

Aufgabe 1

a) $\blacktriangleright$ Wahrscheinlichkeiten berechnen

Du sollst mit Hilfe eines Baumdiagramms die Wahrscheinlichkeit, dass ein Kunde einen Rabatt von 10% erhält, berechnen.

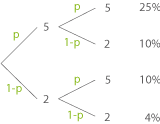Diagramm mit Wahrscheinlichkeiten und Ergebnissen in einem Entscheidungsbaum.

Dem Baumdiagramm kannst du entnehmen, dass es zwei Pfade für einen Rabatt von 10% gibt. Multipliziere jeweils die Wahrscheinlichkeiten entlang des Pfads und addiere dann die Wahrscheinlichkeiten der beiden Pfade.

$\begin{array}[t]{rll} P(10\,\%)&=&p \cdot (1-p) + (1-p) \cdot p \\[5pt] &=&p - p^2 + p - p^2 \\[5pt] &=&2p - 2 p^2 \end{array}$

Die Wahrscheinlichkeit, dass ein Kunde 10% Rabatt erhält, beträgt $2p - 2 p^2$ .

b) $\blacktriangleright$ Erwartungswert berechnen

Ein Kunde kann entweder 4%, 10% oder 25% Rabatt erhalten. Die Zufallsvariable $X$ kann die Werte 4, 10 und 25 annehmen. Du sollst den Erwartungswert von $X$ bestimmen.

Für den Erwartungswert einer Zufallsvariable $X$ mit Ergebnisraum $\Omega = \left\{x_1 , \ldots, x_n \right\}$ gilt folgende Formel

$E(X) = \displaystyle\sum\limits_{i=1}^{n} x_i \cdot P(X=x_i)$

Berechne zunächst die Wahrscheinlichkeiten der möglichen Ergebnisse. Die Wahrscheinlichkeit für 10% hast du bereits in Aufgabenteil a) berechnet. Nutze für die anderen Wahrscheinlichkeiten das Baumdiagramm.

$P(X=4) = (1-p) \cdot (1-p) = 1 - 2p + p^2$
$P(X=10) = 2p - 2 p^2$
$P(X=25) = p^2$

Berechne nun mit der angegebenen Formel den Erwartungswert.

$\begin{array}[t]{rll} E(X)&=&4 \cdot (1 - 2p + p^2) + 10 \cdot (2p - 2 p^2) + 25p^2 \\[5pt] &=&4-8p+4p^2+20p - 20p^2 + 25p^2\\[5pt] &=&9p^2 + 12p +4 \end{array}$

Der Erwartungswert ist $9p^2 + 12p +4$ .

c) $\blacktriangleright$ Wert für $\boldsymbol{p}$ bestimmen

Der Geschäftsführer will, dass im Mittel 16% Rabatt gewährt werden. Du sollst den Wert für $p$ bestimmen, sodass dies erfüllt ist.

Das bedeutet, dass der erwartete Rabatt 16% betragen soll, für den gerade berechneten Erwartungswert soll also gelten:

$\begin{array}[t]{rll} 16&=&E(X) \\[5pt] 16&=&9p^2 + 12p +4 \quad \scriptsize \mid\; -16\\[5pt] 0&=& 9p^2 + 12p -12 \end{array}$

Löse diese Gleichung mit Hilfe der abc-Formel oder mit dem solve-Befehl deines CAS, beachte dabei, dass $p$ eine Wahrscheinlichkeit ist und somit $p \in [0,1]$ gilt.

$\begin{array}[t]{rll} p_{1,2}&=&\dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\[5pt] &=&\dfrac{-12 \pm \sqrt{12^2-4\cdot 9 \cdot (-12)}}{2\cdot 9} \\[5pt] &=&\dfrac{-12 \pm \sqrt{144+432}}{18} \\[5pt] &=&\dfrac{-12 \pm \sqrt{576}}{18} \\[5pt] &=&\dfrac{-12 \pm 24}{18} \\[5pt] p_1 &=&\dfrac{-12 + 24}{18} \ = \ \dfrac{12}{18}\ = \ \dfrac{2}{3} \\[5pt] \Big(p_2 &=&\dfrac{-12 - 24}{18} \ = \ \dfrac{-36}{18} \ = \ -2\Big) \end{array}$

Mathematische Gleichung zur Lösung einer Wahrscheinlichkeit.

Damit im Mittel 16% Rabatt gewährt werden, muss die Wahrscheinlichkeit $p=\frac{2}{3}$ betragen.

d) $\blacktriangleright$ Anzahl an Kunden berechnen

Du sollst die Anzahl der Kunden bestimmen, die mindestens am Glücksrad drehen müssen, damit mit mindestens 99%iger Wahrscheinlichkeit mindestens einer der Kunden den niedrigsten Rabatt erhält. Dabei erhält ein Kunde mit einer Wahrscheinlichkeit von $\frac{1}{9}$ den niedrigsten Rabatt.

Das entspricht der Aussage, dass mit weniger als 1% Wahrscheinlichkeit alle Kunden einen Rabatt von 10% oder 25% erhalten. Die Wahrscheinlichkeit nicht den geringsten Rabatt zu erhalten, berechnest du über das Gegenereignis.

$1- \dfrac{1}{9} = \dfrac{8}{9}$

Mathematisch formuliert sieht die Aussage folgendermaßen aus: $\left(1- \dfrac{1}{9}\right)^n \lt 0,01$ .

Löse diese Gleichung nach $n$ auf um die gesuchte Anzahl an Kunden zu berechnen.

Mathematische Gleichung zur Lösung einer Ungleichung mit Variablen.

Es müssen also mindestens 40 Kunden am Glücksrad drehen, damit mit 99% Wahrscheinlichkeit mindestens ein Kunde den niedrigsten Rabatt erhält.

e) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Du sollst die Wahrscheinlichkeit berechnen, dass mindestens 10 und höchstens 25 der 180 Kunden den niedrigsten Rabatt erhalten.

Sei $Z$ die Anzahl der Kunden, die den niedrigsten Rabatt erhalten. Die Zufallsvariable $Z$ kann als binomialverteilt angenommen werden, da das Zufallsexperiment genau zwei mögliche Ausgänge hat, ein Kunde erhält den niedrigsten Rabatt oder nicht. Außerdem können die Kunden als unabhängig angenommen werden. Somit ist $Z$ binomialverteilt mit $n=180$ und $p=\frac{1}{9}$ .

Du sollst also folgende Wahrscheinlichkeit berechnen: $P(10 \leq Z \leq 25)$ .

Dafür kannst du die kumulierte Binomialverteilung deines CAS verwenden.

menu 5: Wahrscheinlichkeit 5: Verteilungen E: Binomial Cdf

Mathematische Berechnung mit einer Software, die eine binomiale Verteilung anzeigt.

Die Wahrscheinlichkeit, dass mindestens 10 und höchstens 25 der 180 Kunden den niedrigsten Rabatt erhalten, beträgt 89,75 %.

Aufgabe 2

a) $\blacktriangleright$ Entscheidungsregel bestimmen

Du sollst die Entscheidungsregel für die Hypothese II „Mindestens 15% der Kunden sind bereit, die App zu nutzen.“ auf einem Niveau von $\alpha=0,1$ bestimmen.

$H_0: \quad p \geq 0,15$

Sei die Zufallsvariable $X$ die Anzahl der Kunden aus $M = \{0; 1; \ldots; 200\}$ , die bereit sind die App zu nutzen.

Die Zufallsvariable $X$ kann als binomialverteilt angenommen werden, da ein Kunde entweder bereit ist die App zu nutzen oder nicht. Es gibt also nur zwei mögliche Ausgänge des Zufallsexperiments. Außerdem werden die Kunden als unabhängig angenommen. Ein Erfolg steht hier für einen Kunden, der bereit ist die App zu nutzen. Die Zufallsvariable $X$ ist also binomialverteilt mit $B_{200;0,15}$ .

Für den Ablehnungsbereich gilt demnacht: $\overline{A} = \{0;1; \ldots; k-1\}$ .

Die Wahrscheinlichkeit für weniger als $k$ Kunden, die bereit sind die App zu nutzen, soll höchstens 10% betragen.

$P(X \leq k-1)\leq 0,1$

Du kannst $k$ durch systematisches Probieren bestimmen.

menu 5: Wahrscheinlichkeit 5: Verteilungen E: Binomial Cdf

Tabelle mit Berechnungen zur Binomialverteilung und entsprechenden Wahrscheinlichkeiten.

Der größtmögliche Ablehnungsbereich ist $\overline{A}=\{0;\ldots; 23\}$ . Der zugehörige Annahmebereich lautet $A=\{24;\ldots; 200\}$ .

Bei mehr als 23 Kunden, die bereit wären die App zu nutzen, kann die Hypothese angenommen werden.

b) $\blacktriangleright$ Entscheide, ob Kosten oder Image mehr Gewicht in Hypothese II hat

Du sollst entscheiden, ob die Kostenfrage oder der Imageverlust zur Wahl der Hypothese II geführt hat.

Der Imageverlust wird als schwerwiegender erachtet, weil du durch das Signifikanzniveau beim Hypothesentest den Fehler beschränkst die Nullhypothese fälschlicherweise abzulehnen. Das heißt in diesem Fall bei Hypothese II, dass du mit einer Wahrscheinlichkeit von höchstens 10 % nicht in die App investierst, obwohl eigentlich der geforderte Anteil der Kunden die App nutzen würde. In diesem Fall würdest du einen Imageverlust riskieren.

Aufgabengruppe 2

Aufgabe 1

a) $\blacktriangleright$ Mengen schraffieren

Du sollst die Fläche schraffieren, die zum Ereignis $\overline{M}\cap S$ gehört. In Worten lautet dieses Ereignis „nicht $M$ geschnitten $S$ “, das entspricht der Fläche von $S$ , die nicht in $M$ enthalten ist.

Venn-Diagramm mit zwei Mengen M und S, die sich überlappen, mit schraffierter Fläche in der Schnittmenge.

b) $\blacktriangleright$ Mengen die Ereignis beschreiben

Du sollst die Mengen finden, die das Ereignis E beschreiben.

E: „Mindestens eins der Ereignisse $M$ und $S$ tritt ein.“

Die Menge II und V beschreiben das Ereignis E, da

II $M \cup S$ bedeutet es tritt $M$ , $S$ oder $M$ und $S$ ein. Also mindestens eins der beiden Ereignisse tritt ein.

V $(M \cap S)\cup (M \cap \overline{S}) \cup (\overline{M} \cap S )$ bedeutet, $M$ und $S$ oder $M$ und $\overline{S}$ oder $\overline{M}$ und $S$ treten ein.

c) $\blacktriangleright$ Entscheide, welche Wahrscheinlichkeit größer ist

Du hast die folgenden Wahrscheinlichkeiten gegeben und sollst entscheiden, welche der beiden größer ist.

$p_1 = P(\text{Mobiltelefon} \mid \text{über 65})$
$p_2 = P(\text{über 65} \mid \text{Mobiltelefon})$

Die Formel der bedingten Wahrscheinlichkeit lautet wie folgt:

$P(A \mid B) = \dfrac{P(A \cap B)}{P(B)}$

Für die Wahrscheinlichkeiten gilt:

$\begin{array}[t]{rll} p_1&=&P(\text{Mobiltelefon} \mid \text{über 65}) \\[5pt] &=&\dfrac{P(\text{Mobiltelefon} \cap \text{über 65})}{P(\text{über 65})}\\[10pt] p_1&=&P(\text{über 65} \mid \text{Mobiltelefon}) \\[5pt] &=&\dfrac{P(\text{Mobiltelefon} \cap \text{über 65})}{P(\text{Mobiltelefon})} \end{array}$

Da $P(\text{Mobiltelefon}) = 0,9$ und $P(\text{über 65})=0,24$ , wird bei $p_1$ durch eine kleinere Zahl dividiert. Der Zähler der Brüche ist identisch. Somit folgt, dass $p_1 > p_2$ .

d) $\blacktriangleright$ Vierfeldertafel

Du sollst eine Vierfeldertafel erstellen, sodass das Ereignis $E$ mit einer Wahrscheinlichkeit von 98% eintritt.

Es gilt also:

$P(E) = 0,98$
$P(\overline{E}) = 1- P(E) = 0,02$

Das Gegenereignis zu $E$ ist „Weder $S$ noch $M$ tritt ein.“: $\overline{M} \cap \overline{S}$ .

Daraus folgt: $\overline{M} \cap \overline{S} = 0,02$

Außerdem kannst du den Kreisdiagrammen folgende Wahrscheinlichkeiten entnehmen:

$P(S) = 0,24 \quad \Rightarrow \quad P(\overline{S}) = 1-0,24 = 0,76$
$P(M) = 0,9 \quad \Rightarrow \quad P(\overline{M}) = 0,1$

Trage diese Wahrscheinlichkeiten in die Vierfeldertafel ein und vervollständige diese dann entsprechend.

	$M$	$\overline{M}$
$S$			0,24
$\overline{S}$		0,02	0,76
	0,9	0,1	1

Nutze die bereits bekannten Wahrscheinlichkeiten in der Vierfeldertafel um die noch fehlenden zu berechnen:

$P(S \cap \overline{M}) = 0,1 - 0,02 = 0,08$
$P(S \cap M) = 0,24 - 0,08 = 0,16$
$P(\overline{S} \cap M) = 0,9 - 0,16 = 0,74$

Für die vollständige Vierfeldertafel erhältst du dann

	$M$	$\overline{M}$
$S$	0,16	0,08	0,24
$\overline{S}$	0,74	0,02	0,76
	0,9	0,1	1

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Du sollst nun noch die Wahrscheinlichkeit $P_S(M)$ berechnen. Nutze die Vierfeldertafel, um die gesuchte Wahrscheinlichkeit zu berechnen.

$\begin{array}[t]{rll} P_S(M)&=&\dfrac{P(S \cap M)}{P(S)} \\[5pt] &=&\dfrac{0,16}{0,24} \\[5pt] &=&\dfrac{2}{3} \end{array}$

Aufgabe 2

a) $\blacktriangleright$ Wahrscheinlichkeit berechnen

In Deutschland besitzen $\frac{2}{3}$ der Senioren ein Mobiltelefon. Du sollst die Wahrscheinlichkeit berechnen, dass unter 30 zufällig ausgewählten Senioren mindestens 17 und höchstens 23 ein Mobiltelefon besitzen. Die Anzahl der Senioren, die ein Mobiltelefon besitzen, kann als binomialverteilt angenommen werden, da ein Senior entweder ein Mobiltelefon besitzt oder nicht. Außerdem werden die Senioren als unabhängig angenommen. Die Anzahl $X$ der Senioren ist somit binomialverteilt mit $n=30$ und $p=\frac{2}{3}$ . Die Wahrscheinlichkeit $P(17 \leq X \leq 23)$ kannst du mit deinem CAS berechnen.

menu 5: Wahrscheinlichkeit 5: Verteilungen E: Binomial Cdf

Screenshot einer Berechnung mit einer binomialen Verteilungsfunktion.

Die Wahrscheinlichkeit, dass mindestens 17 und höchstens 23 Senioren ein Mobiltelefon besitzen, beträgt 75,015%.

b) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Von den 30 Senioren im Publikum besitzen 24 ein Mobiltelefon. Es werden zufällig drei der Senioren ausgewählt. Du sollst die Wahrscheinlichkeit bestimmen, dass genau zwei der ausgewählten Senioren ein Mobiltelefon besitzen.

Das entspricht einem Urnenmodell mit zwei Gruppen ohne Zurücklegen. Aus der Gruppe mit Mobiltelefon werden zwei ausgewählt $\binom{24}{2}$ , aus der Gruppe ohne Mobiltelefon wird einer ausgewählt $\binom{6}{1}$ und insgesamt werden aus der gesamten Menge drei ausgewählt $\binom{30}{3}$ .

Die gesuchte Wahrscheinlichkeit lautet demnach

$\dfrac{\binom{6}{1}\cdot \binom{24}{2}}{\binom{30}{3}}$ $= \dfrac{\frac{6!}{5!\cdot 1!}\cdot \frac{24!}{2! \cdot 22!}}{\binom{30}{3}} \approx 0,40788$

Zu 40,788 % werden genau zwei Senioren mit Mobiltelefon ausgewählt.

Aufgabe 3

$\blacktriangleright$ Verkaufspreis berechnen

Du sollst den Preis des Typ Y4 berechnen, damit die Handelskette im Mittel 97€ Gewinn beim Verkauf der Modelle Y3 und Y4 erzielt. Der erwartete Gewinn soll also 97€ betragen.

Für den Erwartungswert einer Zufallsvariable $X$ mit Ergebnisraum $\Omega = \left\{x_1 , \ldots, x_n \right\}$ gilt folgende Formel

$E(X) = \displaystyle\sum\limits_{i=1}^{n} x_i \cdot P(X=x_i)$

Du kannst der Aufgabenstellung entnehmen, dass die Wahrscheinlichkeit, dass das Modell Y3 verkauft wird 26% beträgt. Da das Modell Y3 im Einkauf 250€ gekostet hat und nun für 199€ verkauft wird, beträgt der Gewinn -51€.

Stelle die Gleichung für den Erwartungswert auf und forme nach dem Gewinn $G$ für das Modell Y4 um.

$\begin{array}[t]{rll} 97&=&E(X)\\[5pt] 97&=&0,26 \cdot (-51) + (1-0,26) \cdot G\\[5pt] 97&=&-13,26+ 0,74G\quad \scriptsize \mid\; +13,26\\[5pt] 110,26&=&0,74G\quad \scriptsize \mid\; :0,74\\[5pt] G&=&149 \end{array}$

Der Gewinn beim Verkauf des Modells Y4 muss 149€ betragen. Somit gilt für den Verkaufspreis:

Verkaufspreis $= 300 + 149 = 449$ €

Aufgabengruppe 1

Aufgabe 1

a) $\blacktriangleright$ Wahrscheinlichkeiten berechnen

Du sollst mit Hilfe eines Baumdiagramms die Wahrscheinlichkeit, dass ein Kunde einen Rabatt von 10% erhält, berechnen.

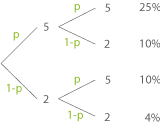Diagramm mit Wahrscheinlichkeiten und Ergebnissen in einer Baumstruktur.

$\begin{array}[t]{rll} P(10%)&=&p \cdot (1-p) + (1-p) \cdot p \\[5pt] &=&p - p^2 + p - p^2 \\[5pt] &=&2p - 2 p^2 \end{array}$

Die Wahrscheinlichkeit, dass ein Kunde 10% Rabatt erhält, beträgt $2p - 2 p^2$ .

b) $\blacktriangleright$ Erwartungswert berechnen

Ein Kunde kann entweder 4%, 10% oder 25% Rabatt erhalten. Die Zufallsvariable $X$ kann die Werte 4, 10 und 25 annehmen. Du sollst den Erwartungswert von $X$ bestimmen.

Für den Erwartungswert einer Zufallsvariable $X$ mit Ergebnisraum $\Omega = \left\{x_1 , \ldots, x_n \right\}$ gilt folgende Formel

$E(X) = \displaystyle\sum\limits_{i=1}^{n} x_i \cdot P(X=x_i)$

$P(X=4) = (1-p) \cdot (1-p) = 1 - 2p + p^2$
$P(X=10) = 2p - 2 p^2$
$P(X=25) = p^2$

Berechne nun mit der angegebenen Formel den Erwartungswert.

$\begin{array}[t]{rll} E(X)&=&4 \cdot (1 - 2p + p^2) + 10 \cdot (2p - 2 p^2) + 25p^2 \\[5pt] &=&4-8p+4p^2+20p - 20p^2 + 25p^2\\[5pt] &=&9p^2 + 12p +4 \end{array}$

Der Erwartungswert ist $9p^2 + 12p +4$ .

c) $\blacktriangleright$ Wert für $\boldsymbol{p}$ bestimmen

Der Geschäftsführer will, dass im Mittel 16% Rabatt gewährt werden. Du sollst den Wert für $p$ bestimmen, sodass dies erfüllt ist.

Das bedeutet, dass der erwartete Rabatt 16% betragen soll, für den gerade berechneten Erwartungswert soll also gelten:

$\begin{array}[t]{rll} 16&=&E(X) \\[5pt] 16&=&9p^2 + 12p +4 \quad \scriptsize \mid\; -16\\[5pt] 0&=& 9p^2 + 12p -12 \end{array}$

Löse diese Gleichung mit Hilfe der abc-Formel oder mit dem solve-Befehl deines CAS, beachte dabei, dass $p$ eine Wahrscheinlichkeit ist und somit $p \in [0,1]$ gilt.

Mathematik-Software zeigt die Lösung einer Gleichung mit zwei Lösungen für p an.

Damit im Mittel 16% Rabatt gewährt werden, muss die Wahrscheinlichkeit $p=\frac{2}{3}$ betragen.

d) $\blacktriangleright$ Anzahl an Kunden berechnen

$1- \dfrac{1}{9} = \dfrac{8}{9}$

Mathematisch formuliert sieht die Aussage folgendermaßen aus: $\left(1- \dfrac{1}{9}\right)^n \lt 0,01$ .

Löse diese Gleichung nach $n$ auf um die gesuchte Anzahl an Kunden zu berechnen.

Mathematische Berechnung im Software-Interface mit einer Ungleichung und einer Lösung für n.

Es müssen also mindestens 40 Kunden am Glücksrad drehen, damit mit 99% Wahrscheinlichkeit mindestens ein Kunde den niedrigsten Rabatt erhält.

e) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Du sollst die Wahrscheinlichkeit berechnen, dass mindestens 10 und höchstens 25 der 180 Kunden den niedrigsten Rabatt erhalten.

Du sollst also folgende Wahrscheinlichkeit berechnen: $P(10 \leq Z \leq 25)$ .

Dafür kannst du die kumulierte Binomialverteilung deines CAS verwenden.

Action Distribution/Inv. Dist. Discrete binomialCDf

Screenshot einer mathematischen Berechnung in einer Software mit dem Ergebnis einer binomialen Verteilungsfunktion.

Die Wahrscheinlichkeit, dass mindestens 10 und höchstens 25 der 180 Kunden den niedrigsten Rabatt erhalten, beträgt 89,75 %.

Aufgabe 2

a) $\blacktriangleright$ Entscheidungsregel bestimmen

Du sollst die Entscheidungsregel für die Hypothese II „Mindestens 15% der Kunden sind bereit, die App zu nutzen.“ auf einem Niveau von $\alpha=0,1$ bestimmen.

$H_0: \quad p \geq 0,15$

Sei die Zufallsvariable $X$ die Anzahl der Kunden aus $M = \{0; 1; \ldots; 200\}$ , die bereit sind die App zu nutzen.

Für den Ablehnungsbereich gilt demnacht: $\overline{A} = \{0;1; \ldots; k-1\}$ .

Die Wahrscheinlichkeit für weniger als $k$ Kunden, die bereit sind die App zu nutzen, soll höchstens 10% betragen.

$P(X \leq k-1)\leq 0,1$

Du kannst $k$ durch systematisches Probieren bestimmen.

Action Distribution/Inv. Dist. Discrete binomialCDf

Screenshot einer Berechnung mit binomialCDF in einer mathematischen Software.

Der größtmögliche Ablehnungsbereich ist $\overline{A}=\{0;\ldots; 23\}$ . Der zugehörige Annahmebereich lautet $A=\{24;\ldots; 200\}$ .

Bei mehr als 23 Kunden, die bereit wären die App zu nutzen, kann die Hypothese angenommen werden.

b) $\blacktriangleright$ Entscheide, ob Kosten oder Image mehr Gewicht in Hypothese II hat

Du sollst entscheiden, ob die Kostenfrage oder der Imageverlust zur Wahl der Hypothese II geführt hat.

Aufgabengruppe 2

Aufgabe 1

a) $\blacktriangleright$ Mengen schraffieren

Venn-Diagramm mit zwei sich überlappenden Kreisen, beschriftet mit M und S. Der überlappende Bereich ist gelb gestrichelt.

b) $\blacktriangleright$ Mengen die Ereignis beschreiben

Du sollst die Mengen finden, die das Ereignis E beschreiben.

E: „Mindestens eins der Ereignisse $M$ und $S$ tritt ein.“

Die Menge II und V beschreiben das Ereignis E, da

II $M \cup S$ bedeutet es tritt $M$ , $S$ oder $M$ und $S$ ein. Also mindestens eins der beiden Ereignisse tritt ein.

V $(M \cap S)\cup (M \cap \overline{S}) \cup (\overline{M} \cap S )$ bedeutet, $M$ und $S$ oder $M$ und $\overline{S}$ oder $\overline{M}$ und $S$ treten ein.

c) $\blacktriangleright$ Entscheide, welche Wahrscheinlichkeit größer ist

Du hast die folgenden Wahrscheinlichkeiten gegeben und sollst entscheiden, welche der beiden größer ist.

$p_1 = P(\text{Mobiltelefon} \mid \text{über 65})$
$p_2 = P(\text{über 65} \mid \text{Mobiltelefon})$

Die Formel der bedingten Wahrscheinlichkeit lautet wie folgt:

$P(A \mid B) = \dfrac{P(A \cap B)}{P(B)}$

Für die Wahrscheinlichkeiten gilt:

Da $P(\text{Mobiltelefon}) = 0,9$ und $P(\text{über 65})=0,24$ , wird bei $p_1$ durch eine kleinere Zahl dividiert. Der Zähler der Brüche ist identisch. Somit folgt, dass $p_1 > p_2$ .

d) $\blacktriangleright$ Vierfeldertafel

Du sollst eine Vierfeldertafel erstellen, sodass das Ereignis $E$ mit einer Wahrscheinlichkeit von 98% eintritt.

Es gilt also:

$P(E) = 0,98$
$P(\overline{E}) = 1- P(E) = 0,02$

Das Gegenereignis zu $E$ ist „Weder $S$ noch $M$ tritt ein.“: $\overline{M} \cap \overline{S}$ .

Daraus folgt: $\overline{M} \cap \overline{S} = 0,02$

Außerdem kannst du den Kreisdiagrammen folgende Wahrscheinlichkeiten entnehmen:

$P(S) = 0,24 \quad \Rightarrow \quad P(\overline{S}) = 1-0,24 = 0,76$
$P(M) = 0,9 \quad \Rightarrow \quad P(\overline{M}) = 0,1$

Trage diese Wahrscheinlichkeiten in die Vierfeldertafel ein und vervollständige diese dann entsprechend.

	$M$	$\overline{M}$
$S$			0,24
$\overline{S}$		0,02	0,76
	0,9	0,1	1

Nutze die bereits bekannten Wahrscheinlichkeiten in der Vierfeldertafel um die noch fehlenden zu berechnen:

$P(S \cap \overline{M}) = 0,1 - 0,02 = 0,08$
$P(S \cap M) = 0,24 - 0,08 = 0,16$
$P(\overline{S} \cap M) = 0,9 - 0,16 = 0,74$

Für die vollständige Vierfeldertafel erhältst du dann

	$M$	$\overline{M}$
$S$	0,16	0,08	0,24
$\overline{S}$	0,74	0,02	0,76
	0,9	0,1	1

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Du sollst nun noch die Wahrscheinlichkeit $P_S(M)$ berechnen. Nutze die Vierfeldertafel, um die gesuchte Wahrscheinlichkeit zu berechnen.

$\begin{array}[t]{rll} P_S(M)&=&\dfrac{P(S \cap M)}{P(S)} \\[5pt] &=&\dfrac{0,16}{0,24} \\[5pt] &=&\dfrac{2}{3} \end{array}$

Aufgabe 2

a) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Action Distribution/Inv. Dist. Discrete binomialCDf

Berechnung der binomialen kumulativen Verteilungsfunktion mit Ergebnissen.

Die Wahrscheinlichkeit, dass mindestens 17 und höchstens 23 Senioren ein Mobiltelefon besitzen, beträgt 75,015%.

b) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Die gesuchte Wahrscheinlichkeit lautet demnach

$\dfrac{\binom{6}{1}\cdot \binom{24}{2}}{\binom{30}{3}}$ $= \dfrac{\frac{6!}{5!\cdot 1!}\cdot \frac{24!}{2! \cdot 22!}}{\binom{30}{3}} \approx 0,40788$

Zu 40,788 % werden genau zwei Senioren mit Mobiltelefon ausgewählt.

Aufgabe 3

$\blacktriangleright$ Verkaufspreis berechnen

Du sollst den Preis des Typ Y4 berechnen, damit die Handelskette im Mittel 97€ Gewinn beim Verkauf der Modelle Y3 und Y4 erzielt. Der erwartete Gewinn soll also 97€ betragen.

Für den Erwartungswert einer Zufallsvariable $X$ mit Ergebnisraum $\Omega = \left\{x_1 , \ldots, x_n \right\}$ gilt folgende Formel

$E(X) = \displaystyle\sum\limits_{i=1}^{n} x_i \cdot P(X=x_i)$

Stelle die Gleichung für den Erwartungswert auf und forme nach dem Gewinn $G$ für das Modell Y4 um.

Der Gewinn beim Verkauf des Modells Y4 muss 149€ betragen. Somit gilt für den Verkaufspreis:

Verkaufspreis $= 300 + 149 = 449$ €