Teil A
1
In Sonnenstadt gibt es 6000 Einfamilienhäuser, von denen 2400 mit einer Holzpelletheizung ausgestattet sind. Bei zwei Dritteln der Einfamilienhäuser mit Holzpelletheizung ist diese mit einer solarthermischen Anlage kombiniert.  aller Einfamilienhäuser sind weder mit einer Holzpelletheizung noch mit einer solarthermischen Anlage ausgestattet.
aller Einfamilienhäuser sind weder mit einer Holzpelletheizung noch mit einer solarthermischen Anlage ausgestattet.
a)
Stelle zu der beschriebenen Situation eine vollständig ausgefüllte Vierfeldertafel auf.
(3 BE)
b)
Ein zufällig ausgewähltes Einfamilienhaus ist mit einer solarthermischen Anlage ausgestattet. Mit welcher Wahrscheinlichkeit hat es eine Holzpelletheizung?
(2 BE)
2
Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen  und
und  sowie deren Gegenereignissen
sowie deren Gegenereignissen  und
und  dar.
dar.
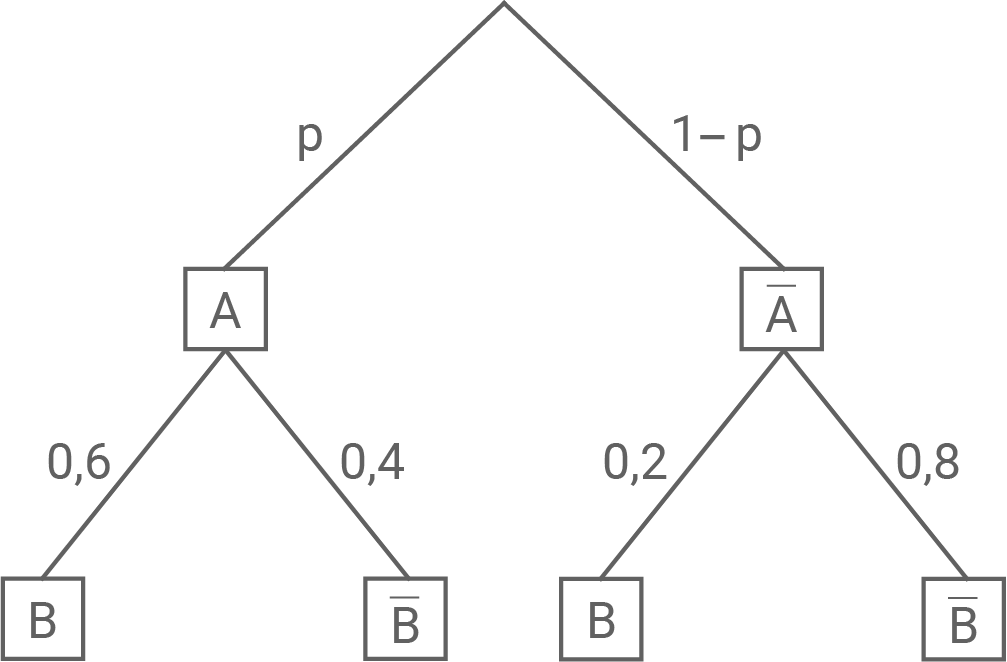

a)
Bestimme den Wert von  so, dass das Ereignis
so, dass das Ereignis  bei diesem Zufallsexperiment mit der Wahrscheinlichkeit
bei diesem Zufallsexperiment mit der Wahrscheinlichkeit  eintritt.
eintritt.
(2 BE)
b)
Ermittle den größtmöglichen Wert, den die Wahrscheinlichkeit von  annehmen kann.
annehmen kann.
(3 BE)
(10 BE)
1
a)
Ein zufällig ausgewähltes Einfamilienhaus aus Sonnenstadt ist mit einer Holzpelletheizung ausgestattet.
Ein zufällig ausgewähltes Einfamilienhaus aus Sonnenstadt ist mit einer solarthermischen Anlage ausgestattet.
Aus der Aufgabenstellung folgt direkt:
b)
Mit Hilfe der Vierfeldertafel folgt für die gesuchte Wahrscheinlichkeit:
![\(\begin{array}[t]{rll}
P_B(A)&=& \dfrac{P(A\cap B)}{P(B)} \\[5pt]
&=& \dfrac{\frac{4}{15}}{\frac{11}{30}}\\[5pt]
&=& \dfrac{8}{11}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4ecd6f881c89a7a32ac9822571e30c0f5a896be3a3e949545b0df7c10493f72c_light.svg)
2
a)
Mit den Pfadregeln folgt für die gesuchte Wahrscheinlichkeit:
b)
Mit Hilfe von Aufgabenteil a) folgt für die Wahrscheinlichkeit von  in Abhängigkeit von
in Abhängigkeit von  folgende Funktion:
folgende Funktion:
 Diese Funktion beschreibt eine Gerade mit positiver Steigung. Die Wahrscheinlichkeit von
Diese Funktion beschreibt eine Gerade mit positiver Steigung. Die Wahrscheinlichkeit von  ist somit für den maximalen Wert von
ist somit für den maximalen Wert von  am größten, das heißt für
am größten, das heißt für  Damit ist
Damit ist 
 der größtmögliche Wert, den die Wahrscheinlichkeit von
der größtmögliche Wert, den die Wahrscheinlichkeit von  annehmen kann.
annehmen kann.