Teil B

Ein Unternehmen stellt Kunststoffteile her. Erfahrungsgemäß sind $4\,\%$ der hergestellten Teile fehlerhaft. Die Anzahl fehlerhafter Teile unter zufällig ausgewählten kann als binomialverteilt angenommen werden.

$50$ Kunststoffteile werden zufällig ausgewählt. Bestimme für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

$A:$

„Genau zwei der Teile sind fehlerhaft.“

$B:$

„Mindestens $6\,\%$ der Teile sind fehlerhaft.“

(3 BE)

Die Kunststoffteile werden aus Kunststoffgranulat hergestellt. Nach einem Wechsel des Granulats vermutet der Produktionsleiter, dass sich der Anteil der fehlerhaften Teile reduziert hat. Um einen Anhaltspunkt dafür zu gewinnen, ob die Vermutung gerechtfertigt ist, soll die Nullhypothese „Der Anteil der fehlerhaften Teile beträgt mindestens $4\,\%$ ." auf der Grundlage einer Stichprobe von 200 Teilen auf einem Signifikanzniveau von $5\,\%$ getestet werden.

Bestimme die zugehörige Entscheidungsregel.

(4 BE)

Das neue Granulat ist teurer als das vorherige. Gib an, welche Überlegung zur Wahl der Nullhypothese geführt haben könnte, und begründe deine Angabe.

(3 BE)

Für ein Spiel wird ein Glücksrad verwendet, das drei farbige Sektoren hat. Der Tabelle können die Farben der Sektoren und die Größen der zugehörigen Mittelpunktswinkel entnommen werden.

Farbe	Mittelpunktswinkel
Blau	$180^{\circ}$
Rot	$120^{\circ}$
Grün	$60^{\circ}$

Für einen Einsatz von 5 Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler dreimal die gleiche Farbe, werden ihm 10 Euro ausgezahlt. Erzielt er drei verschiedene Farben, wird ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.

Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist $\frac{1}{6}.$ Zeige, dass die Wahrscheinlichkeit dafür, dass drei verschiedene Farben erzielt werden, ebenfalls $\frac{1}{6}$ beträgt.

(2 BE)

Bei dem Spiel ist zu erwarten, dass sich die Einsätze der Spieler und die Auszahlungen auf lange Sicht ausgleichen. Berechne den Betrag, der ausgezahlt wird, wenn drei verschiedene Farben erscheinen.

(3 BE)

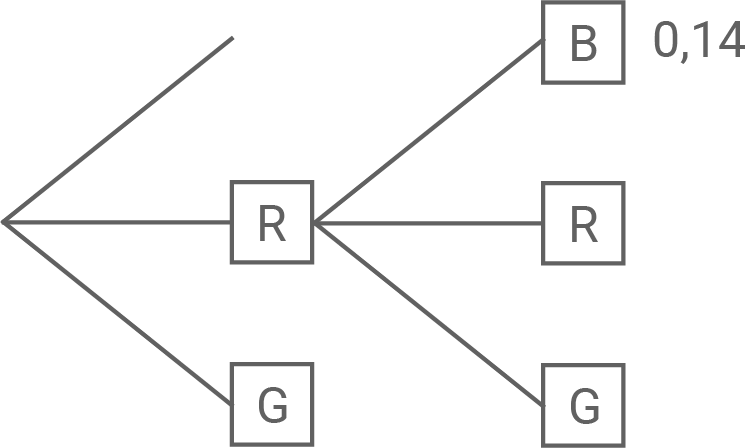
Die Größen der Sektoren werden geändert. Dabei werden der grüne und der rote Sektor verkleinert, wobei der Mittelpunktswinkel des roten Sektors wieder doppelt so groß wie der des grünen Sektors ist. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die beiden ersten Drehungen beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.

Bestimme die Größe des zum grünen Sektor gehörenden Mittelpunktswinkels.

(5 BE)

(20 BE)

Die Zufallsgröße $X$ beschreibt die Anzahl der fehlerhaften Teile in einer Stichprobe von $50$ Kunststoffteilen und ist binomialverteilt mit $n=50$ und $p=0,04.$ Für die gesuchten Wahrscheinlichkeiten ergibt sich:

$\begin{array}[t]{rll} P(A)&=& P(X=2) \\[5pt] &\approx& 0,2762 \\[5pt] &=& 27,62\,\% \end{array}$

$\begin{array}[t]{rll} P(B)&=& P(X\geq 0,06\cdot 50) \\[5pt] &=& P(X\geq 3) \\[5pt] &=& 1- P(X\leq 2) \\[5pt] &\approx& 1-0,6767 \\[5pt] &=& 0,3233 \\[5pt] &=& 32,33\,\% \\[5pt] \end{array}$

Die Zufallsgröße $X_p$ beschreibt die Anzahl der fehlerhaften Teile in einer Stichprobe von $200$ Kunststoffteilen und ist binomialverteilt mit $n=200$ und unbekanntem $p.$ Für die Nullhypothese gilt $p=0,04.$ Gesucht ist die größte Anzahl fehlerhafter Teile $k,$ sodass folgende Ungleichung gilt:

$P(X_{0,04} \leq k) \leq 0,05$

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$\begin{array}[t]{rll} P(X_{0,04}\leq 3)&\approx& 0,0395 \\[5pt] P(X_{0,04}\leq 4)&\approx& 0,0950 \\[5pt] \end{array}$

Somit wird die Nullhypothese verworfen, wenn von den $200$ Teilen höchstens $3$ fehlerhaft sind.

Durch die Wahl der Nullhypothese $H_0: p\geq 0,04$ und des Signifikanzniveaus von $5\,\%$ wird die Wahrscheinlichkeit dafür, dass fälschlicherweise davon ausgegangen wird, dass das neue Granulat besser ist, obwohl es eigentlich eine schlechtere oder gleichschlechte Fehlerquote wie das alte hat, auf maximal $5\,\%$ begrenzt.
Das Unternehmen will somit die Wahrscheinlichkeit dafür, aufgrund des Tests fälschlicherweise von einer Reduzierung der Fehlerquote auszugehen, möglichst niedrig halten.

Für die Wahrscheinlichkeiten der einzelnen Farben gilt:

$\begin{array}[t]{rll} P(„\text{Blau}“)&=& \dfrac{180^{\circ}}{360^{\circ}} \\[5pt] &=& \dfrac{1}{2} \\[10pt] P(„\text{Rot}“)&=& \dfrac{120^{\circ}}{360^{\circ}} \\[5pt] &=& \dfrac{1}{3} \\[10pt] P(„\text{Grün}“)&=& \dfrac{60^{\circ}}{360^{\circ}} \\[5pt] &=& \dfrac{1}{6} \end{array}$

Das mehrmalige Drehen des Glücksrades kann mit dem Modell des „Ziehen mit Zurücklegen“ beschrieben werden. Somit folgt für die gesuchte Wahrsheinlichkeit $p:$

$\begin{array}[t]{rll} p&=& 3! \cdot \dfrac{1}{2}\cdot \dfrac{1}{3}\cdot \dfrac{1}{6} \\[5pt] &=& \dfrac{1}{6}\\[5pt] \end{array}$

Damit der erwartete Gewinn $E(G)$ Null beträgt, folgt für den Betrag $a,$ der ausgezahlt wird, wenn drei verschiedene Farben erscheinen:

Rechenweg anzeigen

$a = 20\,€$

Die Wahrscheinlichkeit, den grünen Sektor zu drehen, beträgt nun $p \lt \frac{1}{6}.$ Die Wahrscheinlichkeit für den roten Sektor ist somit gegeben durch $2p,$ womit sich für die Wahrscheinlichkeit des blauen Sektors $1-(2p +p) = 1-3p$ ergibt.
Mit der Pfadmultiplikationsregel und mit Hilfe der im Baumdiagramm angegebenen Pfadwahrscheinlichkeit ergibt sich folgende Rechnung:

Rechenweg anzeigen

$0 = -6p^2+2p-0,14$

Mit der $abc$ -Formel folgt weiter:

Rechenweg anzeigen

$\begin{array}[t]{rll} p_1&=&\dfrac{7}{30} \\[5pt] p_2&=&\dfrac{1}{10} \end{array}$

Da $\frac{7}{30} \gt \frac{1}{6}$ und $\frac{1}{10} \lt \frac{1}{6}$ gilt, kommt nur $p_2= \frac{1}{10}$ infrage. Für die Größe des neuen Mittelpunktswinkels des grünen Sektors folgt somit:

$\dfrac{1}{10} \cdot 360^{\circ} = 36^{\circ}$