Teil A

Gegeben ist die Funktion $f:x \mapsto \sqrt{1-\text{ln}\,x}$ mit maximaler Definitionsmenge $D$ .

Bestimme $D$ .

(2 BE)

Bestimme den Wert $x\in D$ mit $f(x)=2$ .

(2 BE)

Zeige, dass der Graph der in $\mathbb{R}$ definierten Funktion $g: x \mapsto x^2 \cdot \text{sin}\,x$ punktsymmetrisch bezüglich des Koordinatenursprungs ist, und gib den Wert des Integrals $\displaystyle\int_{-\pi}^{\pi}\,x^2\cdot \text{sin}\, x \; \mathrm dx$ an.

(3 BE)

Skizziere im Bereich $-1\leq x\leq 4$ den Graphen einer in $\mathbb{R}$ definierten Funktion $f$ mit den folgenden Eigenschaften:

$f$ ist nur an der Stelle $x = 3$ nicht differenzierbar.
$f(0) =2$ und für die Ableitung $f‘$ von $f$ gilt: $f‘(0)=-1$ .
Der Graph von $f$ ist im Bereich $-1\lt x\lt 3$ linksgekrümmt.

(3 BE)

Gegeben ist eine in $\mathbb{R}$ definierte ganzrationale Funktion $f$ dritten Grades, deren Graph $G_f$ an der Stelle $x = 1$ einen Hochpunkt und an der Stelle $x = 4$ einen Tiefpunkt besitzt.

Begründe, dass der Graph der Ableitungsfunktion $f‘$ von $f$ eine Parabel ist, welche die $x$ -Achse in den Punkten $(1\mid 0)$ und $(4\mid 0)$ schneidet und nach oben geöffnet ist.

(3 BE)

Begründe, dass $2,5$ die $x$ -Koordinate des Wendepunkts von $G_f$ ist.

(2 BE)

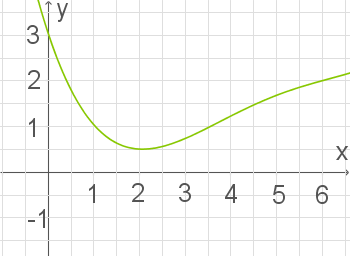
Die Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .

Graph einer Funktion mit einem grünen Verlauf auf einem karierten Hintergrund.

Abb. 1

Bestimme mithilfe der Abbildung 1 einen Näherungswert für $\displaystyle\int_{3}^{5}\, f(x)\,\mathrm dx$ .

(2 BE)

Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3) =0$

Gib mithilfe der Abbildung 1 einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an.

(1 BE)

Zeige, dass $F(b)=\displaystyle\int_{3}^{b}f(x)\;\mathrm dx$ mit $b\in\mathbb{R}$ gilt.

(2 BE)

(20 BE)

Bildnachweise [nach oben]

[1]

$\blacktriangleright$ Maximalen Definitionsbereich bestimmen

Du sollst den maximalen Definitionsbereich der Funktion $f:\, x\mapsto \sqrt{1-\ln x}$ bestimmen.
Hierzu betrachtest du zuerst das Argument der Wurzel: $1-\ln x$ . Dieses darf nicht negativ werden bzw. muss immer größer oder gleich $0$ sein.

$\begin{array}[t]{rll} 0&\leq & 1-\ln x &\quad \scriptsize \mid\; +\ln x \\[5pt] \ln x&\leq& 1 &\quad \scriptsize \mid\; e \\[5pt] x &\leq & e \end{array}$

Somit hast du $x$ zumindest auf einer Seite eingegrenzt. Ein weiteres Problem stellt der natürliche Logarithmus dar. Dessen Argument darf nicht negativ oder $0$ sein. Daraus erhältst du:

$\begin{array}[t]{rll} x&\gt & 0 &\quad \scriptsize \; \end{array}$

$x$ ist nun auf beiden Seiten durch Bedingungen eingeschränkt und du kannst den Definitionsbereich angeben:

$\begin{array}[t]{rll} D&=& ] 0,\,e ] &\quad \scriptsize \; \end{array}$

$\blacktriangleright$ Gleichung lösen

Du sollst die Stelle $x$ im Definitionsbereich bestimmen, für welche $f(x)=2$ gilt. Du erhältst folgende Gleichung:

$\begin{array}[t]{rll} 2&=& \sqrt{1-\ln x} &\quad \scriptsize \mid\; {}^2 \\[5pt] 4&=& 1-\ln x &\quad \scriptsize \mid\; +\ln x \; -4 \\[5pt] \ln x &=& -3 &\quad \scriptsize \mid\; e \\[5pt] x &=& e^{-3} \\[5pt] \end{array}$

$x=\mathrm e^{-3}$ ist Lösung der Gleichung und die gesuchte Stelle.

$\blacktriangleright$ Punktsymmetrie nachweisen

Du sollst nachweisen, dass der Graph der Funktion $g:\, x\mapsto x^2\cdot\sin x$ punktsymmetrisch zum Ursprung ist.
Für einen punktsymmetrischen Graphen gilt, für jede Stelle im Definitonsbereich, $g(-x)=-g(x)$ :

$\begin{array}[t]{rll} f(-x)&=& -x^2\cdot \sin x\\[5pt] -f(x)&=& -x^2\cdot \sin x \end{array}$

Vollständige Lösung anzeigen

Der Graph der Funktion $f$ ist somit punktsymmetrisch zum Koordinatenursprung.

$\blacktriangleright$ Integral berechnen

Du sollst den Wert eines Integrals berechnen. Da die Bestimmung einer Stammfunktion schwierig ist, nutzt du die Punktsymmetrie des Graphen. Du teilst das Integral auf:

$\begin{array}[t]{rll} \int\limits_{-\pi}^\pi x^2\cdot \sin x\; dx&=& ... \end{array}$

Vollständige Lösung anzeigen

Die Beträge der beiden Integrale beschreiben den Inhalt der Fläche, die im jeweiligen Intervall vom Graphen und der $x$ -Achse eingeschlossen werden. Wegen der Punktsymmetrie des Graphen zum Urpsrung, sind diese Flächen gleich groß. Eine der beiden liegt unterhalb der $x$ -Achse, weshalb der Integralwert negativ ist, der andere liegt oberhalb der $x$ -Achse, sodass der zugehörige Integralwert positiv ist.
Die beiden Integralwerte haben also den gleichen Betrag aber unterschiedliche Vorzeichen und heben sich damit gegenseitig auf:

$\begin{array}[t]{rll} \int\limits_{-\pi}^0 x^2\cdot \sin x\; dx + ... \end{array}$

Vollständige Lösung anzeigen

Der Wert des Integrals beträgt somit $0$ .

$\blacktriangleright$ Graph skizzieren

Du sollst den Graphen einer Funktion skizzieren, welcher folgende Bedingungen erfüllt:

$f(x)$ ist auf $\mathbb{R}$ definiert.
$f$ ist nur an der Stelle $x=3$ nicht differenzierbar.
$f(0)=2$ und für die Ableitung $f‘$ von $f$ gilt: $f‘(0)=-1$ .
Der Graph von $f$ ist im Bereich $-1\lt x\lt 3$ linksgekrümmt.

Der erste Punkt bedeutet, dass $f$ an jeder Stelle einen Funktionswert besitzen muss. Da $f$ aber bei $x=3$ nicht differenzierbar sein soll, muss der Graph an dieser Stelle einen Knick aufweisen. Wähle also am besten eine zusammengesetzte Funktion, die aus zwei Teilen besteht.

Wegen des vierten Punkts, bietet sich für den Bereich $x \lt 3$ eine nach oben geöffnete Parabel an. Wegen der dritten Bedingung muss die Parabel durch den Punkt $P(0\mid2)$ verlaufen und dort die Steigung $-1$ besitzen. Letzteres bedeutet, dass es in diesem Punkt eine Tangente mit der Steigung $-1$ an die Parabel gibt. Die Tangente und den Punkt $P$ kannst du zur Orientierung in das Koordinatensystem einzeichnen.

Für den Bereich $x \geq 3$ ist nur wichtig, dass die Funktion in diesem Bereich keine Definitionslücken aufweist. Es kann sich also beispielsweise um eine Gerade handeln.

Folgendes Schaubild erfüllt beispielsweise alle Bedingungen:

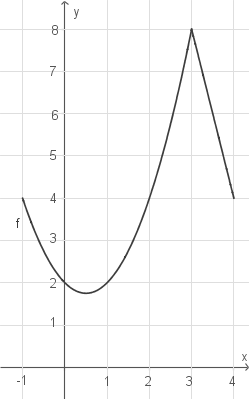Diagramm einer Parabel mit Achsenbeschriftungen x und y.

Abb. 1: Skizze des Funktionsgraphen

$\blacktriangleright$ Eigenschaften der Ableitung begründen

Du sollst begründen, dass der Graph der ersten Ableitung von $f$ eine Parabel ist, die Nullstellen $1$ und $4$ besitzt und nach oben geöffnet ist. Dazu überlegst du, was die Eigenschaften von $f$ für die erste Ableitung bedeuten.

$f$ ist eine ganzrationale Funktion dritten Grades, daher muss die erste Ableitungsfunktion von $f$ eine ganzrationale Funktion zweiten Grades sein. Der zugehörige Graph einer solchen Funktion ist eine Parabel.
Der Graph von $f$ besitzt zwei Extrempunkte an den Stellen $x=1$ und $x=4$ . Mit dem notwendigen Kriterium für Extrempunkte muss die erste Ableitungsfunktion an diesen Stellen eine Nullstelle besitzen. Die Parabel schneidet die $x$ -Achse also in den Punkten $(1\mid 0)$ und $(4\mid 0).$
Der Extrempunkt an der Stelle $x=1$ ist ein Hochpunkt, hier muss die Ableitung also einen Vorzeichenwechsel von positiv zu negativ haben. Der Graph der Parabel verläuft daher für $x \lt 1$ oberhalb der $x$ -Achse und anschließend unterhalb der $x$ -Achse.
Analog gilt für den Tiefpunkt des Graphen von $f$ an der Stelle $x=4$ , dass die erste Ableitung hier einen Vorzeichenwechsel von negativ zu positiv aufweisen muss. Die Parabel muss daher nach oben geöffnet sein.

$\blacktriangleright$ Wendestelle begründen

Du sollst begründen, dass $x=2,5$ die Wendestelle des Graphen von $f$ ist. Für eine Wendestelle gibt es ebenfalls ein notwendiges Kriterium und ein hinreichendes Kriterium. An einer Wendestelle muss die zweite Ableitung eine Nullstelle mit Vorzeichenwechsel haben.
Nutze aus, dass der Graph der ersten Ableitung eine Parabel und somit symmetrisch ist. Da die zweite Ableitung die Steigung des Graphen der ersten Ableitung beschreibt, muss die Steigung des Graphen der ersten Ableitung an dieser Stelle $x=2,5$ die Steigung Null haben, damit die zweite Ableitung Null ist.
Die einzige Stelle einer Parabel, welche die Steigung Null besitzt, ist der Scheitelpunkt und liegt genau zwischen den zwei Nullstellen. Die Wendestelle des Graphen von $f$ dementsprechend auch. Du berechnest somit das arithmetische Mittel der beiden Nullstellen für die Wendestelle $x_W$ .

$\begin{array}[t]{rll} x_W&=& \frac{1+4}{2}&\quad \scriptsize \; \\[5pt] &=& \frac{5}{2}=2,5 \end{array}$

Somit liegt die Wendestelle des Graphen von $f$ bei $x=2,5$ .

$\blacktriangleright$ Näherungswert des Integrals bestimmen

Du sollst anhand des Funktionsgraphen einen Näherungswert für das Integral mit den Grenzen $3$ und $5$ bestimmen. Dieses Integral beschreibt den Inhalt der Fläche, die vom Graphen von $f$ , der $x$ -Achse und den Geraden mit $y = 3$ und $y =5$ eingeschlossen wird.

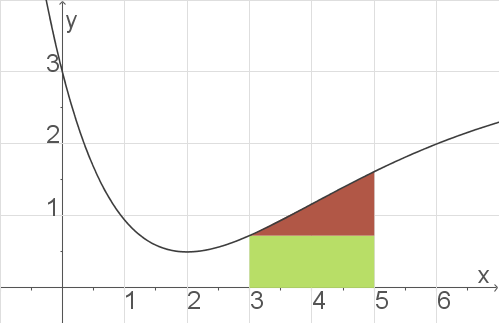Diagramm einer Funktion mit einem hervorgehobenen Bereich in verschiedenen Farben. Achsen sind beschriftet.

Abb. 2: Näherung des Integrals

Zerlege die Fläche in ein Rechteck und eine Fläche, die durch ein Dreieck angenähert werden kann. Die Näherung entspricht somit der Summe der Flächeninhalte. Für das Rechteck mit den Kantenlängen $5-3=2$ und $f(3)$ ergibt sich:

$\begin{array}[t]{rll} A_{4}&=& 2\cdot f(3) \\[5pt] &\approx& 2\cdot 0,75 \\[5pt] &=& 1,5 \end{array}$

Das rechtwinklige Dreieck hat eine Kathete mit dem Rechteck gemeinsam. Die Länge der anderen Kathete ist $f(5)-f(3)$ :

$\begin{array}[t]{rll} A_3&=& \frac{1}{2}\cdot 2\cdot (f(5)-f(3)) \\[5pt] &=& f(5)-f(3) \\[5pt] &\approx& 1,6-0,75 \\[5pt] &=& 0,85 \end{array}$

Für beide Flächen zusammen, beziehungsweise für die Näherung des Integrals, ergibt sich:

$\begin{array}[t]{rll} \int\limits_3^5 f(x)\; dx&\approx& A_4+A_3 \\[5pt] &=& 2,35 \end{array}$

Du kannst einen Näherungswert für das Integral mit ungefähr $2,35$ angeben.

$\blacktriangleright$ Wert der Ableitung bestimmen

Du sollst einen Wert für die Ableitung der Stammfunktion $F$ an der Stelle $x=2$ angeben. Da $F$ eine Stammfunktion von $f$ mit $F(3)=0$ ist, gilt:

$\begin{array}[t]{rll} F‘(x)&=& f(x) \end{array}$

Du kannst somit den Wert der Ableitung von $F$ als Funktionswert von $f$ am Graphen ablesen.

$\begin{array}[t]{rll} F‘(2)&=& f(2) \\[5pt] &\approx& 0,5 \end{array}$

Die Ableitung der Funktion $F$ an der Stelle $x=2$ beträgt ca. $0,5$ .

$\blacktriangleright$ Gleichheit zeigen

Du sollst zeigen, dass $F(b)=\int\limits_3^b f(x)\; \mathrm dx$ gilt. Du kannst hierzu den Hauptsatz der Differential- und Integralrechnung verwenden:

$\displaystyle\int_{a}^{b}f(x) \;\mathrm dx = F(b) -F(a)$

Dabei ist $F$ eine Stammfunktion von $f$ . Wende diesen Satz auf das gegebene Integral an. Zusätzlich hast du noch die Information gegeben, dass $F(3) =0$ gilt. Damit erhältst du insgesamt folgende Rechnung:

$\begin{array}[t]{rll} \displaystyle\int_{3}^{b} f(x)\; \mathrm dx&=& F(b) -F(3) &\quad \scriptsize \mid\; F(3)=0 \\[5pt] &=& F(b)-0 \\[5pt] &=& F(b) \\[5pt] \end{array}$

Damit gilt also $\displaystyle \int_3^b f(x)\; \mathrm dx = F(b)$ .

Bildnachweise [nach oben]

[1]

[2]