Teil B

Nach einem Bericht zur Allergieforschung aus dem Jahr 2008 litt damals in Deutschland jeder vierte bis fünfte Einwohner an einer Allergie. $41\,\%$ aller Allergiker reagierten allergisch auf Tierhaare. Kann aus diesen Aussagen gefolgert werden, dass 2008 mindestens $10\,\%$ der Einwohner Deutschlands auf Tierhaare allergisch reagierten? Begründe deine Antwort.

(3 BE)

Nach einer aktuellen Erhebung leiden $25\,\%$ der Einwohner Deutschlands an einer Allergie. Aus den Einwohnern Deutschlands werden $n$ Personen zufällig ausgewählt.

Bestimme, wie groß $n$ mindestens sein muss, damit mit einer Wahrscheinlichkeit von mehr als $99\,\%$ mindestens eine der ausgewählten Personen an einer Allergie leidet.

(4 BE)

Im Folgenden ist $n=200$ . Die Zufallsgröße $X$ beschreibt die Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden. Bestimme die Wahrscheinlichkeit dafür, dass der Wert der binomialverteilten Zufallsgröße $X$ höchstens um eine Standardabweichung von ihrem Erwartungswert abweicht.

(5 BE)

Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von $39,5\,\%$ ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von $85\,\%$ positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von $35\,\%$ ebenfalls positiv.

Ermittle, welcher Anteil der Bevölkerung Deutschlands demnach allergisch auf Tierhaare reagiert.

(Ergebnis: $9\,\%$ )

(4 BE)

Eine aus der Bevölkerung Deutschlands zufällig ausgewählte Person wird getestet; das Testergebnis ist positiv. Berechne die Wahrscheinlichkeit dafür, dass diese Person tatsächlich an einer Tierhaarallergie leidet.

(2 BE)

Aus der Bevölkerung Deutschlands wird eine Person zufällig ausgewählt und getestet. Beschreibe das Ereignis, dessen Wahrscheinlichkeit im Sachzusammenhang mit dem Term $0,09\cdot 0,15 + 0,91\cdot 0,35$ berechnet wird.

(2 BE)

(20 BE)

$\blacktriangleright$ Aussage treffen

Du sollst entscheiden, ob es möglich ist zu behaupten, dass mindestens $10\%$ aller Einwohner an einer Tierhaarallergie litten. Die Wahrscheinlichkeit dafür, dass eine Person Allergiker ist, beträgt laut Aufgabenstellung mindestens $P(A)=\frac{1}{5}.$ Betrachtest du weiter die Allergiker mit Tierhaarallergie beträgt die Wahrscheinlichkeit dafür $P(T\mid A)=41\%$ . Für den Anteil der Tierhaarallergiker $P(T)$ ergibt sich:

$\begin{array}[t]{rll} P(T)&=& P(A)\cdot P(T\mid A) \\[5pt] &=& \frac{1}{5}\cdot 0,41 \\[5pt] &=& 0,082 =8,2\% \end{array}$

Aufgrund der Angaben kann man höchstens von einem Mindestanteil von $8,2\,\%$ ausgehen. Es kann also nur sicher gesagt werden:

2008 litten mindestens $8,2\%$ aller Einwohner Deutschlands an einer Tierhaarallergie. Dies sind weniger als $10\%$ . Somit kann man nicht bestätigen, dass mindestens jeder zehnte Einwohner an einer Tierhaarallergie litt.

$\blacktriangleright$ Notwendige Anzahl bestimmen

Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als $99\%$ , mindestens eine der Personen an einer Allergie leidet.
Betrachte dazu die Zufallsgröße $X_n,$ die in einer Stichprobe von $n$ zufällig ausgewählten Einwohnern Deutschlands die Anzahl der Personen beschreibt, die unter einer Allergie leiden.
Da die Anzahl der Einwohner Deutschlands wesentlich größer ist als die Anzahl der befragten Personen kannst du davon ausgehen, dass die Zufallsvariable $X_n$ mit $p=25\%$ und unbekanntem $n$ binomialverteilt ist. Für binomialverteilte Zufallsvariablen gilt folgende Formel für die Wahrscheinlichkeiten:

$P(X=k)= ...$

Vollständige Lösung anzeigen

Da mindestens eine Person an einer Allergie leiden soll, erhältst du eine Ungleichung in $n$ , wobei du, um die Rechnung zu vereinfachen, das Gegenereignis betrachtest:

$n \geq 17$

Vollständige Lösung anzeigen

Da ein ganzzahliges Ergebnis anzugeben ist, müssen mindestens $17$ Personen untersucht werden.

$\blacktriangleright$ Wahrscheinlichkeit für Abweichung vom Erwartungswert bestimmen

Gesucht ist die Wahrscheinlichkeit dafür, dass $X$ höchstens um eine Standardabweichung $\sigma$ vom Erwartungswert $\mu$ abweicht.
Dazu kannst du entweder die Standardabweichung und den Erwartungswert berechnen und anschließend die kumulierte Binomialverteilung verwenden oder die $\sigma$ -Regeln für binomialverteilte Zufallsgrößen anwenden. Beachte, dass du dazu zunächst die Bedingung $\sigma \gt 3$ überprüfen musst.

$\blacktriangleright$ Lösungsweg A: Sigma-Regeln

Berechne dazu die Standardabweichung $\sigma$ mit folgender Formel:

$\sigma = \sqrt{n\cdot p \cdot q}$

$\begin{array}[t]{rll} \sigma_X &=& \sqrt{200\cdot 0,25\cdot 0,75} \\[5pt] &=& \sqrt{37,5} \gt 3 \\[5pt] \end{array}$

Die $\sigma$ -Regeln können also angewendet werden. Gesucht ist die Wahrscheinlichkeit dafür, dass $X$ einen Wert annimmt, der höchstens um eine Standardabweichung $\sigma$ von ihrem Erwartungswert $\mu$ abweicht. Die entsprechende Regel lautet:

Mit $\sigma \gt 3$ gilt für eine binomialverteilte Zufallsgröße $X:$

$P(\mu-1\cdot \sigma \leq X \leq \mu +1\cdot \sigma)$ $\approx 0,683$

Die Wahrscheinlichkeit dafür, dass $X$ einen Wert annimmt, der höchstens um eine Standardabweichung vom Erwartungswert abweicht, beträgt ca. $68,3\,\%.$

$\blacktriangleright$ Lösungsweg B: Kumulierte Binomialverteilung

Bei binomialverteilten Zufallsgrößen gilt für den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ :

$\begin{array}[t]{rll} \mu &=& n\cdot p \\[5pt] &=& 200\cdot 0,25 \\[5pt] &=& 50 \end{array}$

$\begin{array}[t]{rll} \sigma &=& \sqrt{n\cdot p\cdot (1-p)} \\[5pt] &=& \sqrt{200\cdot 0,25\cdot 0,75} \\[5pt] &\approx& 6,12 \end{array}$

Gesucht ist also folgende Wahrscheinlichkeit:

$P(\mu -\sigma \leq X\leq \mu +\sigma )$

Vollständige Lösung anzeigen

Mit einer Wahrscheinlichkeit von $71,17\%$ liegt die Anzahl der Allergiker im $1-\sigma$ Intervall und weicht somit maximal um eine Standardabweichung vom Erwartungswert ab.

$\blacktriangleright$ Bevölkerungsanteil mit Tierhaarallergie berechnen

Du sollst berechnen, mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Testperson an einer Tierhaarallergie leidet. Dazu betrachtest du die zwei Ereignisse und trägst sie in einem Baumdiagramm auf:

$T$ : Test ist positiv
$H$ : Person reagiert auf Tierhaare allergisch

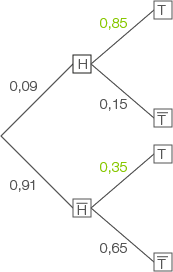Baumdiagramm mit Wahrscheinlichkeiten für verschiedene Ereignisse.

Abb 1: Baumdiagramm zu Aufgabe 3

Somit kannst du $P(H)$ berechnen mit:

$P(H)=0,09$

Vollständige Lösung anzeigen

$9\,\%$ der Bevölkerung reagiert allergisch auf Tierhaare.

$\blacktriangleright$ Wahrscheinlichkeit für korrektes Testergebnis berechnen

Du sollst berechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis korrekt ist. Gesucht ist also die Wahrscheinlichkeit für eine Tierhaarallergie unter der Bedingung, dass der Test positiv ausfällt. Dazu kannst du den Satz von Bayes verwenden:

$P(H\mid T)=\frac{P(T\mid H)\cdot P(H)}{P(T)}$

Die Wahrscheinlichkeit $P(H)=0,09$ hast du oben bereits berechnet. Die Wahrscheinlichkeit für einen positiven Test insgesamt kennst du aus der Aufgabenstellung $P(T)=0,395$ . $P(T\mid H) = 0,85$ ist die Wahrscheinlichkeit für einen positiven Test, falls der getestete Patient eine Tierhaarallergie hat und kann ebenfalls aus der Aufgabenstellung abgelesen werden.

$P(H\mid T) \approx 19,37\,\%$

Vollständige Lösung anzeigen

Mit einer Wahrscheinlichkeit von $19,37\,\%$ ist eine positiv getestete Person wirklich allergisch.

$\blacktriangleright$ Term im Sachzusammenhang interpretieren

Du sollst den Term $p=0,09\cdot 0,15+0,91\cdot 0,35$ im Sachzusammenhang interpretieren. Du erkennst, dass es sich um die Summe der Wahrscheinlichkeiten zweier verschiedener Ereignisse handelt.

1. Teil: $\boldsymbol{0,09\cdot 0,15}$

Die Wahrscheinlichkeit $0,09$ zeigt an, dass eine Person an einer Tierhaarallergie leidet. $0,15$ ist die Wahrscheinlichkeit, dass der Test trotzdem negativ ist.

2. Teil: $\boldsymbol{0,91\cdot 0,35}$

$0,91$ ist die Wahrscheinlichkeit, dass eine Person nicht an einer Tierhaarallergie leidet. $0,35$ zeigt an, dass der Test trotzdem positiv ist.

Zusammenfassend ergibt sich, dass der Term die Wahrscheinlichkeit angibt, dass der Test ein falsches Ergebnis liefert, also die Fehlerquote des Tests.

Bildnachweise [nach oben]

[1]