Teil B

Die Abbildung zeigt modellhaft wesentliche Elemente einer Kletteranlage: zwei horizontale Plattformen, die jeweils um einen vertikal stehenden Pfahl gebaut sind, sowie eine Kletterwand, die an einer der beiden Plattformen angebracht ist.

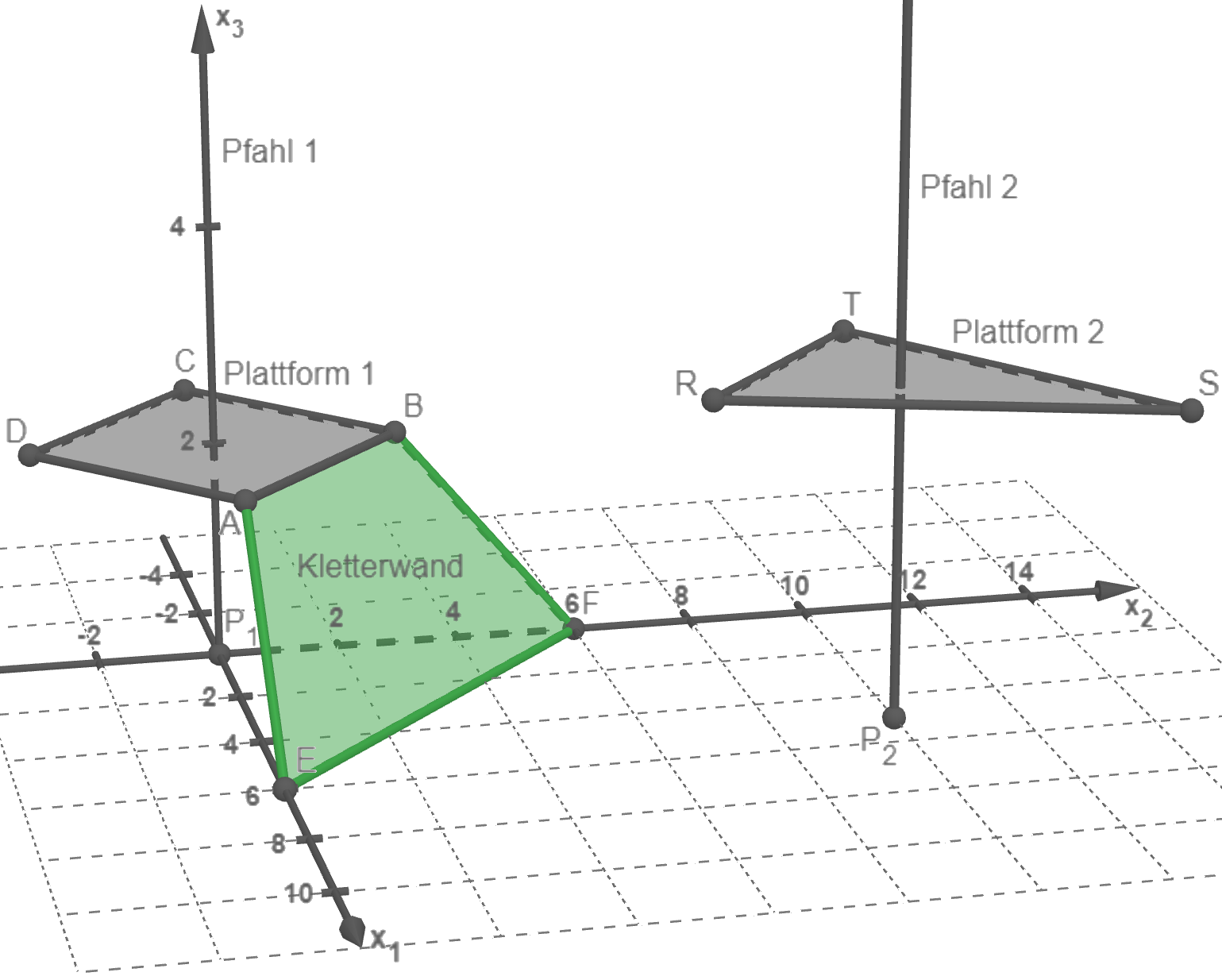Im verwendeten Koordinatensystem beschreibt die $x_1 x_2$ -Ebene den horizontalen Untergrund. Die Plattformen und die Kletterwand werden als ebene Vielecke betrachtet. Eine Längeneinheit entspricht $1\;\text{m}$ in der Wirklichkeit. Die Punkte, in denen die Pfähle aus dem Untergrund austreten, werden durch $P_1(0\mid0\mid 0)$ und $P_2(5\mid10\mid 0)$ dargestellt. Außerdem sind die Eckpunkte $A(3\mid0\mid 2), B(0\mid3\mid 2),$ $E(6\mid0\mid 0),$ $F(0\mid6\mid 0),$ $R(5\mid7\mid 3)$ und $T(2\mid10\mid 3)$ gegeben. Die Materialstärke aller Bauteile der Anlage soll vernachlässigt werden.

In den Mittelpunkten der oberen und unteren Kante der Kletterwand sind die Enden eines Seils befestigt, das $20\,\%$ länger ist als der Abstand der genannten Mittelpunkte. Berechne die Länge des Seils.

(3 BE)

Die Punkte $A,B,E$ und $F$ liegen in der Ebene $L.$ Ermittle eine Gleichung von $L$ in Normalenform.

(zur Kontrolle: $L:2x_1 + 2x_2 + 3x_3- 12 =0$ )

(4 BE)

Zeige, dass die Kletterwand die Form eines Trapezes hat.

(2 BE)

Bestimme die Größe des Winkels, den die Kletterwand mit dem Untergrund einschließt.

(3 BE)

Über ein Kletternetz kann man von einer Plattform zur anderen gelangen. Die vier Eckpunkte des Netzes sind an den beiden Pfählen befestigt. Einer der beiden unteren Eckpunkte befindet sich an Pfahl 1 auf der Höhe der zugehörigen Plattform, der andere untere Eckpunkt an Pfahl 2 oberhalb der Plattform 2. An jedem Pfahl beträgt der Abstand der beiden dort befestigten Eckpunkte des Netzes $1,80\;\text{m}$ . Das Netz ist so gespannt, dass davon ausgegangen werden kann, dass es die Form eines ebenen Vierecks hat.

Berechne den Flächeninhalt des Netzes und erläutere deinen Ansatz.

(3 BE)

Die untere Netzkante berührt die Plattform 2 an der Seite, die durch die Strecke $[RT]$ dargestellt wird. Betrachtet wird der untere Eckpunkt des Netzes, der oberhalb der Plattform 2 befestigt ist. Im Modell hat dieser Eckpunkt die Koordinaten $(5\mid 10\mid h)$ mit einer reellen Zahl $h \gt 3.$ Die untere Netzkante liegt auf der Geraden $g:\overrightarrow{X} =$ $\pmatrix{0\\0\\2}+ \lambda \cdot \pmatrix{5\\10\\h-2},$ $\lambda \in \mathbb{R}.$ Berechne den Abstand des betrachteten Eckpunkts von der Plattform 2.

(5 BE)

(20 BE)

1. Schritt: Koordinaten der Kantenmittelpunkte bestimmen

$\begin{array}[t]{rll} \overrightarrow{OM_1}&=& \dfrac{1}{2}\cdot \left(\overrightarrow{OA} +\overrightarrow{OB}\right) \\[5pt] &=& \dfrac{1}{2}\cdot \left(\pmatrix{3\\0\\2} + \pmatrix{0\\3\\2} \right) \\[5pt] &=& \pmatrix{1,5\\1,5\\2} \\[10pt] \overrightarrow{OM_2}&=& \dfrac{1}{2}\cdot \left(\overrightarrow{OE} +\overrightarrow{OF}\right) \\[5pt] &=& \dfrac{1}{2}\cdot \left(\pmatrix{6\\0\\0} + \pmatrix{0\\6\\0} \right) \\[5pt] &=& \pmatrix{3\\3\\0} \end{array}$

2. Schritt: Länge berechnen

Für die Länge $l$ des Seils folgt somit:

$\begin{array}[t]{rll} l&=& 1,2\cdot \left|\overrightarrow{M_1M_2} \right| \\[5pt] &=& 1,2\cdot \left|\pmatrix{1,5\\1,5\\-2} \right| \\[5pt] &=& 1,2\cdot \sqrt{1,5^2+1,5^2 +(-2)^2} \\[5pt] &\approx& 3,50\;[\text{m}] \end{array}$

Ein möglicher Normalenvektor von $L$ ergibt sich wie folgt:

$\begin{array}[t]{rll} \overrightarrow{n} &=& \overrightarrow{AB}\times \overrightarrow{AE} \\[5pt] &=& \pmatrix{-3\\3\\0}\times \pmatrix{3\\0\\-2} \\[5pt] &=& \pmatrix{ 3\cdot (-2) - 0\cdot 0 \\ 0\cdot 3 -(-3)\cdot (-2) \\ (-3)\cdot 0 - 3\cdot 3 } \\[5pt] &=& \pmatrix{-6\\-6\\-9} \\[5pt] &=& -3\cdot \pmatrix{2\\2\\3} \\[5pt] \end{array}$

Mit Hilfe des gekürtzten Normalenvektors ergibt sich die Gleichung $L:2x_1+2x_2+3x_3-d=0.$ Einsetzen der Koordinaten eines Punktes in der Ebene, beispielsweise $F,$ liefert für $d:$

$\begin{array}[t]{rll} 2\cdot 0 +2\cdot 6 +3 \cdot 0-d&=&0 &\quad \scriptsize \mid\;+d \\[5pt] 12&=& d \end{array}$

Eine Gleichung der Ebene $E$ in Normalenform ist somit wie folgt gegeben:

$L:2x_1+2x_2+3x_3-12=0$

Bei einem Viereck handelt es sich um ein Trapez, wenn zwei gegenüberliegende Seiten parallel sind. Der Abbildung kann entnommen werden, dass das vermutlich die beiden Strecken $[AB]$ und $[EF]$ sind. Zur Überprüfung wird folgende Gleichung betrachtet:

$\begin{array}[t]{rll} \overrightarrow{AB}&=& a\cdot \overrightarrow{EF} \\[5pt] \pmatrix{-3\\3\\0}&=& a\cdot \pmatrix{-6\\6\\0} \end{array}$

Diese Gleichung ist für $a=\frac{1}{2}$ erfüllt. Somit sind die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{EF}$ parallel und die Kletterwand hat die Form eines Trapezes.

Der Untergrund wird durch die $x_1x_2$ -Ebene beschrieben. Ein zugehöriger Normalenvektor ist hier $\overrightarrow{n_1} = \pmatrix{0\\0\\1}.$ Die Kletterwand liegt im Modell in der Ebene $L$ mit dem Normalenvektor $\overrightarrow{n_2} = \pmatrix{2\\2\\3}.$ Mit der Formel für den Schnittwinkel zweier Ebenen folgt für die Größe des gesuchten Winkels:

$\begin{array}[t]{rll} \cos (\alpha)&=& \dfrac{\left| \overrightarrow{n_1} \circ \overrightarrow{n_2} \right|}{\left|\overrightarrow{n_1} \right|\cdot \left|\overrightarrow{n_2} \right| } \\[5pt] \cos (\alpha)&=& \dfrac{\left| \pmatrix{0\\0\\1} \circ \pmatrix{2\\2\\3} \right|}{\left|\pmatrix{0\\0\\1}\right|\cdot \left|\pmatrix{2\\2\\3} \right| } \\[5pt] \cos (\alpha)&=& \dfrac{3}{1 \cdot \sqrt{2^2+2^2+3^2} } \\[5pt] \cos (\alpha)&=& \dfrac{3}{ \sqrt{17} } \\[5pt] \alpha&\approx& 43,3^{\circ} \end{array}$

Da die beiden Pfähle senkrecht zum Untergrund stehen sind sie parallel zueinander. Somit sind auch die beiden Seiten des Netzes, die an den Pfählen befestigt sind, parallel zueinander. Da der Abstand der beiden Eckpunte des Netzes an beiden Pfählen gleichlang sind, bildet das Netz ein Parallelogramm mit $1,8\;\text{m}$ langer Grundseite und einer Höhe, die dem Abstand der beiden Pfähle entspricht. Für die Höhe gilt:

$\begin{array}[t]{rll} h&=& \left|\overrightarrow{P_1P_2} \right| \\[5pt] &=& \left|\pmatrix{5\\10\\0} \right| \\[5pt] &=& \sqrt{5^2+10^2+0^2} \\[5pt] &=& \sqrt{125}\;[\text{m}] \\[5pt] \end{array}$

Für den Flächeninhalt des Netzes folgt somit insgesamt:

$\begin{array}[t]{rll} A&=& 1,8 \cdot h \\[5pt] &=& 1,8\cdot \sqrt{125}\\[5pt] &\approx& 20,12\;[\text{m}^2] \end{array}$

Gesucht ist der Schnittpunkt von $g$ mit der Geraden $h_2,$ auf der im Modell Pfahl 2 liegt. Dazu muss $h$ so bestimmt werden, dass $g$ die Gerade durch die Punkte $R$ und $T$ schneidet, da das Netz die Plattform in dieser Kante berühren soll. Eine Gleichung dieser Geraden lautet:

$\begin{array}[t]{rll} h_1:\overrightarrow{X} &=& \overrightarrow{OR} + \mu\cdot \overrightarrow{RT}\\[5pt] &=& \pmatrix{5\\7\\3} + \mu \cdot \pmatrix{-3\\3\\0} \end{array}$

Gleichsetzen mit der Geradengleichung von $g$ liefert:

Rechenweg anzeigen

$\lambda\cdot \pmatrix{5\\10\\h-2}- \mu \cdot \pmatrix{-3\\3\\0} = \pmatrix{5\\7\\1}$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&5&=& 5\lambda +3\mu \\[5pt] \text{II}\quad&7&=& 10\lambda -3\mu \\[5pt] \text{III}\quad&1&=& (h-2)\cdot \lambda \\[5pt] \end{array}$

Die Rechnung $\text{II}-2\cdot\text{I}$ liefert folgendes Gleichungssystem:

$\(\begin{array}{lrll} \text{I$

Gleichung $\(\text{I$ liefert somit $\mu=\frac{1}{3}.$ Einsetzen in Gleichung $\text{I}$ liefert:

$\begin{array}[t]{rll} 5&=&5\lambda+3\cdot\frac{1}{3} &\quad \scriptsize \mid\;-1 \\[5pt] 4&=&5\lambda &\quad \scriptsize \mid\;:5 \\[5pt] \dfrac{4}{5}&=&\lambda \end{array}$

Einsetzen von $\lambda=\frac{4}{5}$ in Gleichung $\text{III}$ liefert für $h:$

$\begin{array}[t]{rll} 1&=& (h-2)\cdot \dfrac{4}{5} &\quad \scriptsize \mid\; \cdot\frac{5}{4} \\[5pt] 1,25&=& h-2 &\quad \scriptsize \mid\; +2 \\[5pt] 3,25&=& h \end{array}$

Der betrachtete Eckpunkt hat somit die Koordinaten $(5\mid 10 \mid 3,25).$ Da die Plattformen horizontal verlaufen, ergibt sich der Abstand des betrachteten Eckpunktes des Netzes zur Plattform 2 über die Differenz der $x_3$ -Koordinaten. Die Punkte auf der Plattform 2 haben im Modell alle die $x_3$ -Koordinate $3,$ somit beträgt der gesuchte Abstand $3,25-3=0,25\;[\text{m}].$