a)
 Zeigen, dass
Zeigen, dass  zu jedem der drei Terme äquivalent ist
zu jedem der drei Terme äquivalent ist
Hier sollst du zeigen, dass

mit
zu jedem der drei gegebenen Terme äquivalent ist. Da

zu jedem der drei Terme äquivalent sein soll bedeutet dies, dass die drei Terme untereinander
ebenfalls äquivalent sein müssen. Du kannst hierbei also auch zeigen, dass die drei Terme untereinander äqiuvalent sind und anschließend noch , dass

zu einem dieser Terme äqiuvalent ist. Zeige also im ersten Schritt, dass die drei gegebenen Terme äquivalent zueinander sinnd.
Im zweite Schritt zeigst du dann, dass

zu
einem der drei Terme äquivalent ist. Dies kannst du erreichen, indem du beispielsweise die Bruchterme im Funktionsterm auf den
gleichen Nenner bringst.
1. Schritt: Zeigen der Äquivalenz der drei Terme
Willst du hier die Äquivalenz der drei Terme zeigen, so forme den ersten Term wie folgt um:
![\(\begin{array}[t]{rll}
\dfrac{2} {(x+1)\cdot (x+3)}&=& \dfrac{2} {x^2 + 3 \cdot x + 1 \cdot x + 3} \; = \; \dfrac{2} {x^2 +4 \cdot x + 3}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7fbb626464d8ed5055255a8fb7a0323b4064e62b399801d94502c4947e355e90_light.svg)
Hier kannst du sofort sehen, dass die ersten beiden Terme äquivalent sind. Um nun zu zeigen, dass Term 2 und 3 äquivalent sind, musst du den Term im Nenner wie folgt über eine
quadratische Ergänzung zusammenfassen:
![\(\begin{array}[t]{rll}
\dfrac{2} {x^2 +4 \cdot x + 3}&=& \dfrac{2} {(x + 2)^2 - 4 + 3}\;=\;\dfrac{2} {(x + 2)^2 - 1}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ac792934bfc0a5756a9520f4fedc4717332a2d5d1734dfd8ed2489da60085e6e_light.svg)
Kürze den Term nun noch mit

, um die Äquivalenz von Term 2 und Term 3 zu zeigen:
![\(\begin{array}[t]{rll}
\dfrac{2} {(x + 2)^2 - 1}&=& \dfrac{0,5 \cdot 2} {0,5 \cdot \left((x + 2)^2 - 1\right)} = \dfrac{1} {0,5 \cdot (x + 2)^2 - 0,5} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a764980daefb0dab3956670ca2d47328e633059c5d2ce007f9729ad807749c31_light.svg)
Damit hast du gezeigt, dass die in der Aufgabenstellung gegebenen Terme äquivalent zueinander sind.
2. Schritt: Zeigen der Äquivalenz von  und des ersten Terms
und des ersten Terms
Willst du die beiden Bruchterme in

auf den gleichen Nenner bringen, so musst du diese mit dem Nenner des jeweils anderen Bruchs erweitern:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{x+1} - \dfrac{1}{x+3} \;=\; \dfrac{x+3}{(x+1)(x+3)} - \dfrac{x+1}{(x+1)(x+3)} = \dfrac{x+3 - x - 1}{(x+1)(x+3)} = \dfrac{2}{(x+1)(x+3)}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/417d6807ef6cd3652e1fadba2366cbe966358ec867d49fc61d7ee1ea1ca737bb_light.svg)
Damit hast du gezeigt, dass

äquivalent zum ersten gegebenen Term ist. Da alle gegebenen Terme äquivalent sind, ist auch

äquivalent zu diesen.
b)
 Begründen, dass die
Begründen, dass die  -Achse horizontale Asymptote ist
-Achse horizontale Asymptote ist
Willst du zeigen, dass die

-Achse horizontale Asymptote von

ist, so musst du das
Grenzwertverhalten von

untersuchen. Zeige dabei, dass der Graph von

für

gegen
Null konvergiert.
Berechne nun wie folgt die Grenzwerte von

für

:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to\infty} f(x)&=& \lim\limits_{x\to\infty} \left(\underbrace{\dfrac{1}{x+1}}_{\to 0} - \underbrace{\dfrac{1}{x+3}}_{\to 0}\right) = 0\\[5pt]
\lim\limits_{x\to-\infty} f(x)&=&\lim\limits_{x\to-\infty} \left(\underbrace{\dfrac{1}{x+1}}_{\to 0} - \underbrace{\dfrac{1}{x+3}}_{\to 0} \right)= 0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/96287710b3d00b1abdb6a1a9f6b634fda29c7d48ae89d9dbdcdb7065f18fbdf0_light.svg)
Da


gegen Null konvergiert, hast du gezeigt, dass die

-Achse waagrechte Asymptote von

ist.
 Angeben der Gleichungen der vertikalen Asypmtoten
Angeben der Gleichungen der vertikalen Asypmtoten
Ein Graph besitzt an den Stellen vertikale Asymptoten, an denen der Nenner der Funktion

Null. Also in unserem Fall genau an den Werten, an denen die Funktion

Definitionnslücken besitzt. Asymptoten an.
Betrachtest du den gegebenen Definitionsbereich von

näher, so kannst du erkennen, dass

vertikale Asymptoten bei

und

besitzt, da bei diesen Werten einer der beiden Brüche der Funktion

Null wird. Die Gleichungen der vertikalen Asymptoten an

lauten also:
 Bestimmen der Koordinaten des Schnittpunktes mit der
Bestimmen der Koordinaten des Schnittpunktes mit der  -Achse
-Achse
Die Koordinaten des Schnittpunktes mit der

-Achse bestimmst du, in dem du den Funktionswert von

an der Stelle

berechnest.
Das Einsetzen von

ergibt:
![\(\begin{array}[t]{rll}
f(0)&=& \dfrac{1}{0+1} - \dfrac{1}{0+3} = 1 - \dfrac{1}{3} = \dfrac{2}{3}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9a0f6e734840679dee87c9d303baac8e2f895ac86c5e1b1874f740580b0e9d77_light.svg)
Die Koordinaten des Schnittpunkts von

mit der

-Achse lauten also:

c)
 Zeigen, dass
Zeigen, dass  die einzige Nullstelle von
die einzige Nullstelle von  ist
ist
Hier hast du die Funktion

mit
und den Graphen von

gegeben. Weiterhin weißt du, dass für alle


gilt. Nun ergibt sich gemäß der
Quotientenregel für die Ableitung

und

die Beziehung
Deine Aufgabe ist es nun, zu Begründen, dass

die einzige Nullstelle von

ist, unter Verwendung der gegebenen Beziehung und ohne Berechnung von

und

.
Willst du dies hier zeigen, so setze
 gleich Null
gleich Null und vereinfache diesen soweit wie möglich. Untersuche anschließend das gegebene Schaubild des Graphen von

und begründe die Nullstelle bei

. Gehe dazu auf die Eigenschaften einer ganzrationalen Funktion zweiten Grades ein.
1. Schritt: Vereinfachen der Gleichung
Setze den Term für

gleich Null und vereinfache so weit wie möglich:
![\(\begin{array}[t]{rll}
f‘(x)&=&0\\[5pt]
- \dfrac{p‘(x)}{\left(p(x)\right)^2}&=&0 & \scriptsize \quad \mid \cdot \left(p(x)\right)^2\\[5pt]
- p‘(x)&=&0 & \scriptsize \quad \mid : (-1)\\[5pt]
p‘(x)&=&0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5e510d51d1b1fde01f4dd65f19e01e3724e00164d99ef0f53284061a47d069ac_light.svg)
Du siehst hier, dass

überall da Nullstellen besitzt, wo

welche besitzt. Hierbei musst du außerdem noch ausschließen, dass

in dem gegebenem Definitionsberecih nicht null wird.
Setze dazu

und bestimme die Nullstellen von
 2. Schritt: Betrachten des Graphen von
2. Schritt: Betrachten des Graphen von 
Betrachtest du

näher, so kannst du erkennen, dass dieser ein Tiefpunkt mit den Koordinaten

besitzt. Aus der notwendigen Bedingung für Extremstellen weißt du, dass diese sich an den Stellen befinden, an denen die erste Ableitung zur Funktion Nullstellen besitzt. Außerdem handelt es sich bei

um eine ganzrationale Funktion zweiten Grades. Diese besitzt also genau eine Extremstelle.
Da

die Extremstelle

und da

Nullstellen die gleichen Nullstellen wie

besitzt, liegt die einzige Nullstelle von

bei

vor
 Begründen des Monotonieverhaltens und Angeben der Lage und Art des Extrempunktes
Begründen des Monotonieverhaltens und Angeben der Lage und Art des Extrempunktes
Weiterhin sollst du in dieser Aufgabe begründen, dass

in
![\(]-3;-2[\)](https://www.schullv.de/resources/formulas/7c49509ea2426173167296ea580c18d1ecc0db6fb92cfcf08cda8b05d039d0c1_light.svg) streng monoton steigend
streng monoton steigend und in
![\(]-2; -1[\)](https://www.schullv.de/resources/formulas/9fcf779bc6ed6b5fe8864f209b7e9a5cbb566450ee8b812ab256596c299d4d83_light.svg) streng monoton fallend
streng monoton fallend ist. Des Weiteren sollst du
Art und Lage des Extrempunktes von

angeben.
Betrachtest du noch einmal die gegebene Beziehung für

, so kannst du erkennen, dass alleine der Zähler über die
Vorzeichen der Ableitungswerte entscheidet. Dieser entspricht gerade

. Oben hast du herausgefunden, dass

eine ganzrationale Funktion zweiten Grades mit Extremstelle bei

ist.

entspricht also einer
Geraden.
Beachte die Vorzeichen in der Beziehung für

und löse diese Aufgabe anhand der Eigenschaften von

.
1. Schritt: Zeigen der Monotonie von  auf den gegeben Intervallen
auf den gegeben Intervallen

besitzt bei

einen Tiefpunkt. Die Ableitung

besitzt also bei

einen Vorzeichenwechsel von - nach +. Aufgrund der Vorzeichen in der gegeben Beziehung für

ergibt sich, dass

im Intervall von
![\(]-3;-2[\)](https://www.schullv.de/resources/formulas/7c49509ea2426173167296ea580c18d1ecc0db6fb92cfcf08cda8b05d039d0c1_light.svg)
, also von der Definitionslücke bei

bis zur Nullstelle bei

streng monoton steigend sein muss, da

in diesem Bereich unterhalb der

-Achse verläuft.
Analog gilt für den Intervall
![\(]-2;-1[\)](https://www.schullv.de/resources/formulas/a7d7cc0b1b03dbcdff4fd827db4130fb48675abc7999ff9022fa7afe103509aa_light.svg)
, dass

dort streng monoton fallend ist. Hier verläuft

oberhalb der

-Achse und aufgrund der Vorzeichen in der Beziehung für

, verläuft

hier unterhalb der

-Achse.
2. Schritt: Angeben der Lage und Art des Extrempunktes von 
Aus dem ersten Schritt weißt du, dass

im Intervall vor der Extremstelle bei

streng monoton steigend ist und im Intervall nach der Extremstelle streng monoton fallend ist.

besitzt also an der Extremstelle einen Vorzeichenwechsel von + nach -.

besitzt also bei

einen Hochpunkt.
Bestimme durch Einsetzen von

in

die vollständigen Koordinaten des Hochpunkts:
![\(\begin{array}[t]{rll}
f(-2)&=\dfrac{1}{-2+1} - \dfrac{1}{-2+3} = - 1 - 1 = -2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9e160be4f2974d6d703e124e4ef59aec34ed6e94455051d5b7f0375498c7538e_light.svg)
Die vollständigen Koordinaten des Hochpunkts sind also:

.
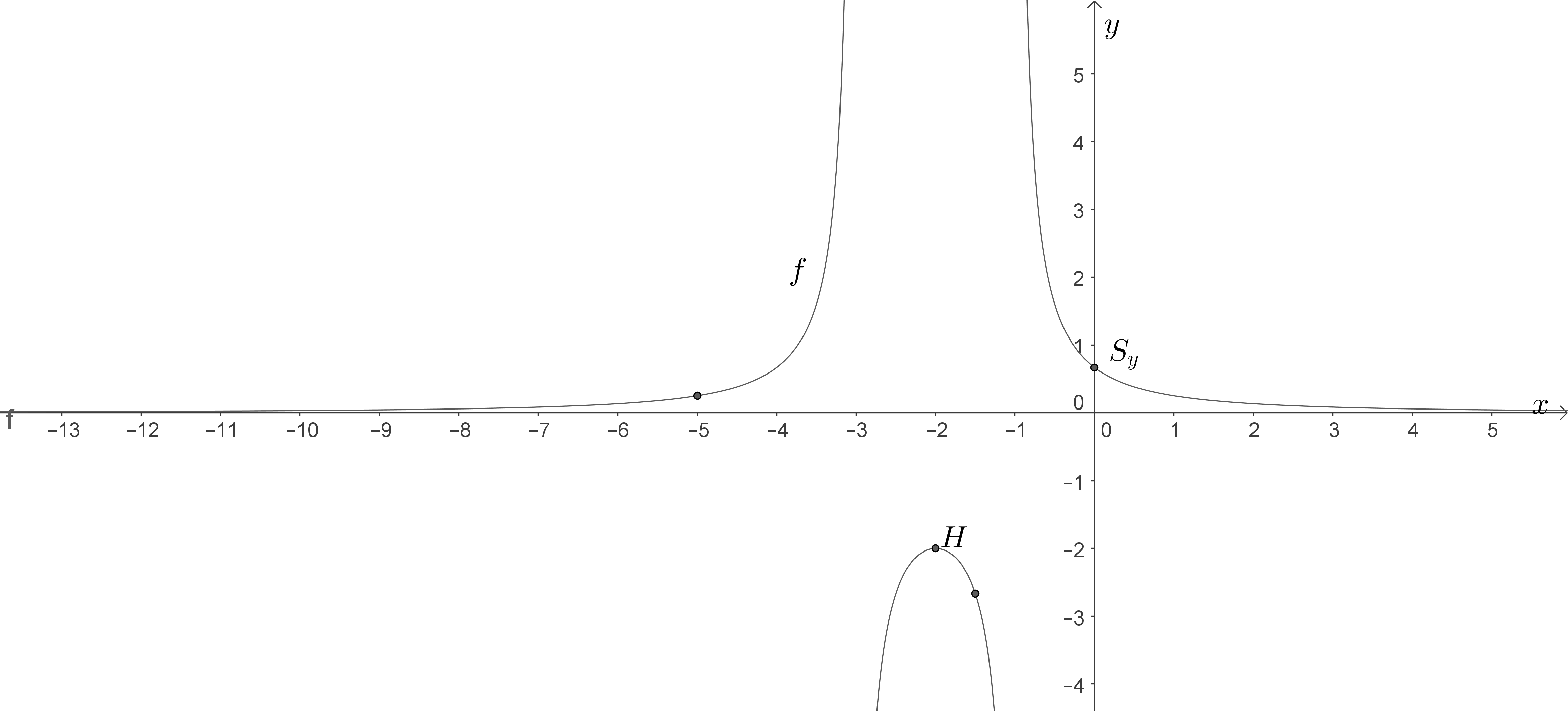
d)
 Berechnen der Funktionswerte und Skizzieren von
Berechnen der Funktionswerte und Skizzieren von 
Berechne zunächst die Funktionswerte

und

. Fasse dann alle Informationen die du bereits für

gesammelt hast zusammen und skizziere den Graphen.
Das weißt du über den Graphen von

:
1. Schritt: Berechnen der Funktionswerte
![\(\begin{array}[t]{rll}
f(-1,5)&=&\dfrac{1}{-1,5 + 1} - \dfrac{1}{-1,5 + 3} = -2 - \frac{2}{3} = -\frac{8}{3}\\[5pt]
f(-5)&=&\dfrac{1}{-5 + 1} - \dfrac{1}{-5 + 3} = -\frac{1}{4} + \frac{1}{2} = \frac{1}{4}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bdaa5b78f2b2879bbb29dd104e56ad17f3001401710898b464cb321b2da2f052_light.svg)
Vergleichst du die eben berechneten Funktionswerte mit den bereits berechneten Werte von oben, so kannst du erkennen, dass jeweils an den Definitionslücken
Vorzeichenwechsel des Graphen

vorliegen. Berücksichtige das beim Zeichnen von

.
2. Schritt: Zeichnen des Graphen 
Der Graph

sollte nun wie unten aussehen:
a)
 Grenzwert anhand des Funktionsterms begründen
Grenzwert anhand des Funktionsterms begründen
Hier ist dir Funktion

gegeben, mit:
Deine Aufgabe ist es dazu, den Grenzwert

anhand des Funktionsterms zu begründen. Betrachte dazu den Funktionsterm genauer und mache dir zunächst Gedanken über das
Grenzwertverhalten der einzelnen Bestandteile.
Der Funktionsterm von

setzt sich wie folgt zusammen:
- Es handelt sich hier um einer Funktion mit Bruch
- Der Zähler des Bruchs ist konstant
- Der Nenner besitzt einen exponentiellen Bestandteil
Betrachtest du die Exponentialfunktion im Nenner des Bruchs, so kannst du erkennen, dass der Exponent für

ebenfalls gegen

strebt. Daraus folgt, dass die Exponentialfunktion gegen

strebt.
Da diese im Nenner des Bruchs steht, wird dieser immer kleiner und konvergiert für

gegen Null. Die konstanten Bestandteile sind bei der Grenzwertbetrachtung zu vernachlässigen.
 Zeigen, dass die Ableitung stets Werte kleiner Null annimmt
Zeigen, dass die Ableitung stets Werte kleiner Null annimmt
Nun sollst du zeigen, dass die erste Ableitung

von

nur Werte
echt kleiner Null annimmt. Das heißt, du sollst zeigen, dass für

gilt.
Bestimme dazu zunächst

über das Ableiten von

nach der
Quotientenregel. Stelle anschließend eine Ungleichung auf und forme soweit um, bis du eine wahre Aussage erhältst.
Beachte beim Lösen der Aufgabe insbesondere die Eigenschaften der Exponentialfunktion.
1. Schritt: Bestimmen der ersten Ableitungsfunktion 
Mit der Quotientenregel ergibt sich hier:
![\(\begin{array}[t]{rll}
h(x)&=& \dfrac{3}{\mathrm e^{x + 1} - 1}\\[5pt]
h‘(x)&=& \dfrac{0 \cdot \left(\mathrm e^{x + 1} - 1\right) - 3 \cdot \left(\mathrm e^{x + 1}\right)}{\left(\mathrm e^{x + 1} - 1\right)^2}\\[5pt]
h‘(x)&=& \dfrac{- 3 \cdot \mathrm e^{x + 1}}{\left(\mathrm e^{x + 1} - 1\right)^2}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/980b93c6745a297eeae235054197a4338bc3ba6129e8b9d733c0d67cce64c6a5_light.svg) 2. Schritt: Zeigen, dass
2. Schritt: Zeigen, dass  gilt
gilt
Stelle nun die Ungleichung auf und forme wie folgt um:
![\(\begin{array}[t]{rll}
h‘(x)\lt & 0\\[5pt]
\dfrac{- 3 \cdot \mathrm e^{x + 1}}{\left(\mathrm e^{x + 1} - 1\right)^2}\lt & 0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1affee50905441b20c599cfc58359ede494ffc8b5a899ee837c28e453a4ae007_light.svg)
Betrachtest du den Nenner von

, so kannst du erkennen, dass dieser aufgrund des Quadrats niemals kleiner Null werden kann. Dieser kann im Folgenden vernachlässigt werden.
![\(\begin{array}[t]{rll}
- 3 \cdot \mathrm e^{x + 1}\lt & 0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8962659699e8d40c885f763b188170bba7c513d7b033dfde5607876db7251ce6_light.svg)
Die Exponentialfunktion nimmt für keinen Wert von

einen Wert kleiner oder gleich Null an. Da diese

multipliziert wird, ist der Term für alle

echt kleiner Null.
b)
 Begründen der Aussagen
Begründen der Aussagen
Gegeben hast du nun die Integralfunktion

mit
Diese Funktion entspricht einer
Stammfunktion von

. Das heißt

entspricht der
ersten Ableitung von

.
Hier sollst du nun begründen, dass folgende beiden Aussagen wahr sind:
- Der Graph von
 ist streng monoton steigend
ist streng monoton steigend
- Der Graph von
 ist rechtsgekrümmt
ist rechtsgekrümmt
1. Der Graph von  ist streng monoton steigend
ist streng monoton steigend
Willst du begründen, dass diese Aussage wahr ist, so betrachte den Funktionsterm von

und begründe, dass

für alle Werte

Funktionswerte echt größer Null annimmt.
Betrachtest du den Nenner von

mit

, so kannst du erkennen, dass dieser im gesamten Definitionsbereich
 positiv
positiv ist. Da der Zähler mit
 konstant
konstant ist, nimmt

nur positive Funktionswerte an und der Graph von

ist streng monoton steigend.
2. Der Graph von  ist rechtsgekrümmt
ist rechtsgekrümmt
Der Graph einer Funktion ist dann rechtsgekrümmt, wenn die erste Ableitung der betreffenden Funktion
monoton fällt.
Da

der ersten Ableitung von

entspricht und da du oben gezeigt hast, dass

gilt, fällt

streng monoton. Daraus folgt für den Graphen von

, dass dieser rechtsgekrümmt ist.
c)
 Angeben der Nullstelle von
Angeben der Nullstelle von 

entspricht einer Integralfunktion. Willst du nun den Nullstelle von

bestimmen, so argumentiere hier mit den
Eigenschaften des Integrals.

ist als Integral über

von

bis zur oberen Grenze

definiert. Du weißt, dass
per Definition für

gelten muss. Das heißt

hat bei

eine Nullstelle. Da

streng monoton steigend ist, ist dies auch die einzige Nullstelle.
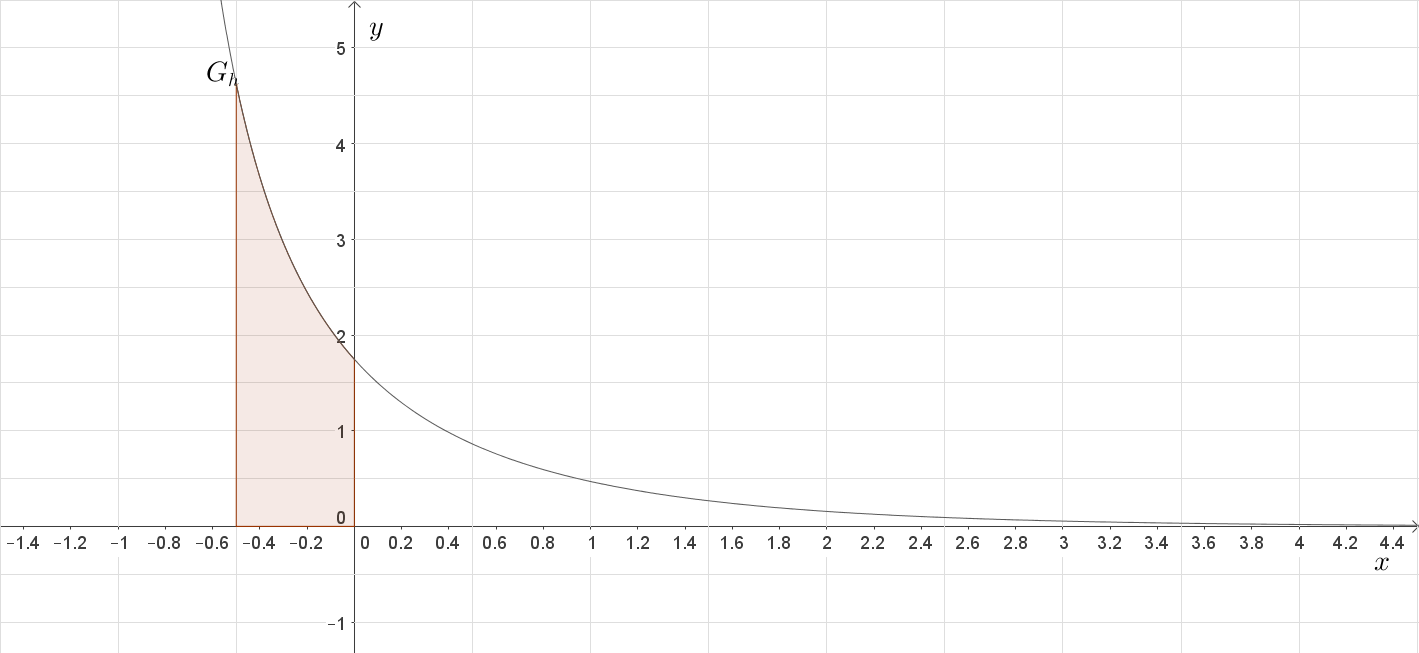
 Näherungsweises bestimmen der Funktionswerte
Näherungsweises bestimmen der Funktionswerte
Nun sollst du die Funktionswerte

und

näherungsweise bestimmen. Da

eine Integralfunktion ist, musst du hier die Fläche unterhalb des Graphen von
 schätzen
schätzen. Achte dabei darauf, dass

ab

definiert ist. Beachte auch insbesondere beim Funktionswert

das Vorzeichen.
Um den Funktionswert

näherungsweise anzugeben, musst du die Fläche zwischen

und

unterhalb des Graphen von

schätzen.
Zählst du jetzt die Kästchen, so kannst du erkennen, dass der Flächeninhalt näherungsweise

ist. Es gilt also

. Das negative Vorzeichen resultiert dabei daraus, dass die obere Integralgrenze mit
 kleiner
kleiner als die untere Integralgrenze mit

ist.
Der Funktionswert

ergibt sich analog. Für diesen gilt näherungsweise:

.
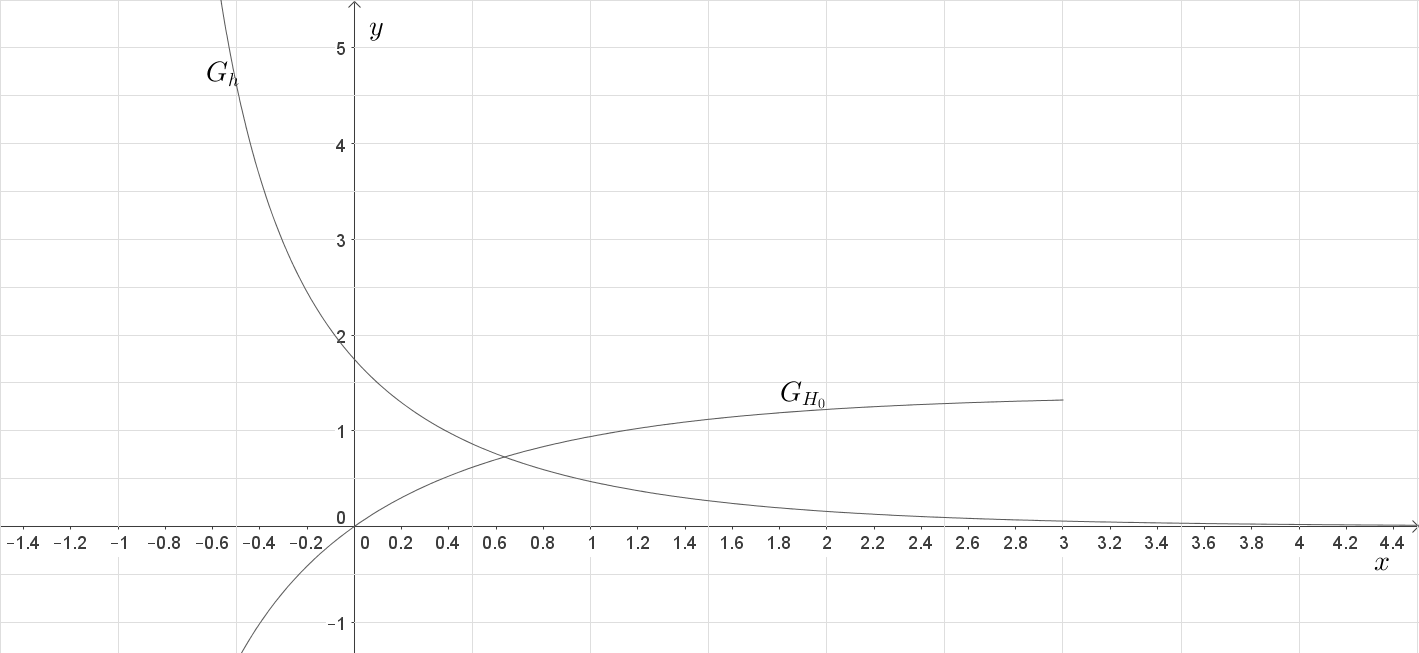
 Skizzieren des Graphen H_0
Skizzieren des Graphen H_0
Nun sollst du den Graphen von

in Abbildung 2 im Bereich

skizzieren. Rufe dir dazu ins Gedächtnis, was du über den Graphen von

weißt:
Anhand dieser Angeben solltest du Abbildung 2 wie folgt ergänzt haben:
a)
 Zeitpunkt, bei dem momentane Schadstoffabbaurate 0,01 Gramm pro Minute beträgt
Zeitpunkt, bei dem momentane Schadstoffabbaurate 0,01 Gramm pro Minute beträgt
Nun soll Funktion

für

die zeitliche Entwicklung des momentanen Schadstoffabbaus von kontaminierten Wasser beschreiben.

bezeichnet dabei die
momentane Schadstoffabbaurate in Gramm pro Minute und

die seit Beginn des Reinigungsvorgangs
vergangene Zeit in Minuten.
Du sollst nun den Zeitpunkt

bestimmen, zu dem die momentane Schadstoffabbaurate auf 0,01 Gramm pro Minute zurückgegangen ist. Setze dazu den Funktionsterm von

mit

gleich und löse nach dem Zeitpunkt

.
Hier ergibt sich:
![\(\begin{array}[t]{rll}
h(x)&=& 0,01\\[5pt]
0,01&=&\dfrac{3}{\mathrm e^{x+1} - 1} & \quad \scriptsize \mid\;\cdot\left(\mathrm e^{x+1} - 1\right)\\[5pt]
0,01 \cdot \left(\mathrm e^{x+1} - 1\right)&=&3\\[5pt]
0,01 \cdot \mathrm e^{x+1} - 0,01&=&3& \quad \scriptsize \mid\;+ 0,01\\[5pt]
0,01 \cdot \mathrm e^{x+1}&=&3,01& \quad \scriptsize \mid\;: 0,01\\[5pt]
\mathrm e^{x+1}&=&301& \quad \scriptsize \mid\;\ln(\,)\\[5pt]
x+1&=&\ln(301)& \quad \scriptsize \mid\;-1\\[5pt]
x&\approx&4,71\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d315f26349c6830002576b1dc08c64a61ab90c07f4a2935b21fffc24376dc5d4_light.svg)
Zum Zeitpunkt

, also nach etwas mehr als 4,5 Minuten beträgt die momentane Schadstoffabbaurate 0,01 Gramm pro Minute.
b)
 Beschreiben wie
Beschreiben wie  aus
aus  hervorgeht
hervorgeht
Hier sollst du bestimmen, wie der Graph der Funktion

, mit
aus dem Graphen der Funktion

hervorgeht. Betrachte dazu den Funktionsterm von

genauer und untersuche, ob dieser in Richtung der Koordinatenachsen
verschoben wurde und ob eine
Streckung des Graphen vorliegt.
Vergleichst du die Funktionsterme von

und

, so kannst du erkennen, dass

wie folgt aus

hervorgegangen ist:
![\(\begin{array}[t]{rll}
k(x)&=& 3 \cdot f(x) - 0,2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e1db002663008739696983f6d03827673b72f5c0613acaf8ef7da010f66d9316_light.svg)
Der Graph von

wurde also mit dem Faktor 3 gestreckt und um 0,2 Einheiten in Richtung der negativen

-Achse verschoben.
c)
 Berechnen des Integralwertes und angeben der Bedeutung im Zusammenhang
Berechnen des Integralwertes und angeben der Bedeutung im Zusammenhang
Der Aufgabenstellung kannst du entnehmen, dass ein Näherungswert für

mit
vorliegt. Im Folgenden sollst du diesen Wert berechnen und dessen Bedeutung im Sachzusammenhang angeben.
Hier musst du also über

integrieren. Beachte dabei, dass beim Bestimmen der Stammfunktion von

folgender Zusammenhang gilt:
Willst du die Bedeutung des berechneten Wertes im Zusammenhang angeben, dann beachte, dass

die momentane Schadstoffabbaurate angibt. Eine Stammfunktion von

gibt also die insgesamt abgebaute Schadstoffmenge in Gramm an.
1. Schritt: Bestimmen einer Stammfunktion für 
Eine Stammfunktion

von

ergibt sich wie folgt:
![\(\begin{array}[t]{rll}
k(x)&=& 3 \cdot \left(\dfrac{1}{x+1} - \dfrac{1}{x+3}\right)-0,2\\
K(x)&=& 3 \cdot \left(\ln(x+1) - \ln(x+3)\right)-0,2 \cdot x
\end{array}\)](https://www.schullv.de/resources/formulas/82e02d6284206d7137ca93acb27d328b0fcf75b4bfe22bdaed39180c9ddee9e2_light.svg) 2. Schritt: Berechnen des Integrals
2. Schritt: Berechnen des Integrals
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{1}\;k(x) \mathrm dx&=& \left[K(x)\right]_0^1\;=\;K(1) - K(0)\\[5pt]
&=& \left(3 \cdot \left(\ln(1+1) - \ln(1+3)\right)-0,2 \cdot 1\right) - \left(3 \cdot \left(\ln(0+1) - \ln(0+3)\right)-0,2 \cdot 0\right)\\[5pt]
&=& \left(3 \cdot \left(\ln(2) - \ln(4)\right)-0,2\right) - \left(3 \cdot \left(\ln(1) - \ln(3)\right)\right)\\[5pt]
&\approx& -2,28 + 3,3\\[5pt]
&=& 1,02\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b5be4f1d97e9960316dec68d29d92332452b5abdfc1348be958fe98e20becdeb_light.svg) 3. Schritt: Angeben der Bedeutung im Sachzusammenhang
3. Schritt: Angeben der Bedeutung im Sachzusammenhang
Es gilt also:

. Das heißt, die Schadstoffmenge hat sich innerhalb einer Minute um 1,02

Gramm verringert.
a)
 Bestimmen der Werte für
Bestimmen der Werte für  und
und 
Der Aufgabenstellung kannst du entnehmen, dass der Graph

der Funktion

, mit

mit

im Punkt

einen
Wendepunkt mit waagrechter Tangente besitzt. Weiterhin ist dir bekannt, dass

ein
weiterer Wendepunkt von

ist. Deine Aufgabe ist es die Parameterwerte für

und

zu bestimmen.
Willst du diese hier bestimmen, so musst du mindestens
2 Bedingungen an

formulieren. Verwende dazu die Informationen über die Wendepunkte und Stelle ein entsprechendes Gleichungssystem auf.
Beachte, dass folgende zwei Bedingungen bei einer Wendestelle

von

erfüllt sein müssen:
- Notwendige Bedingung:

- Hinreichende Bedingung:

1. Schritt: Bestimmen der benötigen Ableitungsfunktionen von 
Verwende zum Ableiten hier die
Faktorregel:
![\(\begin{array}[t]{rll}
f(x)&=& a \cdot x^4 + b \cdot x^3\\[5pt]
f‘(x)&=& 4 \cdot a \cdot x^3 + 3 \cdot b \cdot x^2\\[5pt]
f‘‘(x)&=& 12 \cdot a \cdot x^2 + 6 \cdot b \cdot x\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/749ee2e7a5ce03f0e1de9e37436b495597e82c672baca46fc79649beb267e5eb_light.svg) 2. Schritt: Aufstellen des Gleichungssystems
2. Schritt: Aufstellen des Gleichungssystems
Hier musst du ein Gleichungssystem mit insgesamt 2 Gleichungen aufstellen, um

und

eindeutig bestimmen zu können. Die erste Gleichung ergibt sich aus den Koordinaten von

:

Die zweite Gleichung des Gleichungssystems ergibt sich aus der notwendigen Bedingung für Wendestellen und dem Wendestelle

von

:

Es ergibt sich also folgendes Gleichungssystem:
 3. Schritt: Lösen des Gleichungssystems
3. Schritt: Lösen des Gleichungssystems
Das Gleichungssystem kannst du jetzt wie unten zu sehen ist, über das
Additionsverfahren lösen:

Für die Parameterwerte

und

gilt also:

und

. Der Funktionsterm von

ergibt sich also zu:

.
b)
 Bestimmen der Lage und Art des Extrempunktes
Bestimmen der Lage und Art des Extrempunktes
Hier sollst du nun die Lage und Art des Extrempunktes des Graphen von

bestimmen. Beachte dabei, dass an einer Extremstelle

von

folgende zwei Bedingungen erfüllt sein müssen:
- Notwendige Bedingung:

- Hinreichende Bedingung:

Anhand des Funktionswerts der zweiten Ableitung bei

kann die Art des Extremums festgestellt werden:
 Minimum
Minimum Maximum
Maximum
Gehe also so beim Lösen der Aufgabe vor:
- Bestimme unter Verwendung der Ergebnisse aus a) die benötigten Ableitungsfunktionen
- Bestimme die potentiellen Extremstellen mit Hilfe von
 . Achtung: Bei
. Achtung: Bei  befindet sich eine Wendestelle mit waagrechter Tangente
befindet sich eine Wendestelle mit waagrechter Tangente
- Stelle die Art der Extremstellen mit Hilfe von
 fest
fest
- Bestimme mit
 die vollständigen Koordinaten des Extrempunktes
die vollständigen Koordinaten des Extrempunktes
1. Schritt: Bestimmen der benötigen Ableitungsfunktionen
Mit den Ergebnissen aus Aufgabenteil a) ergeben sich die benötigten Ableitungsfunktionen

und

wie folgt:
![\(\begin{array}[t]{rll}
f‘(x)&=& 4 \cdot 1 \cdot x^3 + 3 \cdot (-2) \cdot x^2 = 4 \cdot x^3 - 6 \cdot x^2 \\[5pt]
f‘‘(x)&=&12 \cdot 1 \cdot x^2 + 6 \cdot (-2) \cdot x = 12 \cdot x^2 -12 \cdot x\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/08df0f3573155194be5afdf0a7eb48ffeda08be583a7048180feae316423c138_light.svg) 2. Schritt: Bestimmen der potentiellen Extremstellen
2. Schritt: Bestimmen der potentiellen Extremstellen
Setze nun

gleich Null und bestimme mit Hilfe des
Satzes vom Nullprodukt die potentiellen Extremstellen von

:
![\(\begin{array}[t]{rll}
f‘(x)&=& 0\\[5pt]
0&=&4 \cdot x^3 - 6 \cdot x^2\\[5pt]
0&=&x^2 \cdot \left(4 \cdot x -6\right)\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b626c26d9cf20b21e83f89ce9a62d558d2dc44376c4c0ca42a663787a50d4879_light.svg)

besitzt also bei

eine
doppelte Nullstelle. Von dieser Stelle weißt du, dass hier der Wendepunkt von

mit waagrechter Tangente liegt.

kommt also
nicht als Extremstelle von

in Frage.
![\(\begin{array}[t]{rll}
0&=&4 \cdot x -6 & \scriptsize \quad \mid + 6\\[5pt]
6&=&4 \cdot x & \scriptsize \quad \mid : 4\\[5pt]
\dfrac{3}{2}&=&x_2
\end{array}\)](https://www.schullv.de/resources/formulas/60b0e534356bede95b9e3a2ea15f10e728af72caf81eeca3ee4693de0b34330f_light.svg)
Es befindet sich also eine potentielle Extremstelle bei

.
3. Schritt: Bestimmen der Art des Extrempunktes und Berechnen der vollständigen Koordinaten
Setze

nun in

ein, um die Art des Extrempunktes zu bestimmen:
![\(\begin{array}[t]{rll}
f‘‘(x_2)&=& 12 \cdot \left(\frac{3}{2}\right)^2 -12 \cdot \frac{3}{2} = 27 - 18 = 9 \gt 0\\[5pt]
6&=&4 \cdot x & \scriptsize \quad \mid : 4\\[5pt]
\frac{3}{2}&=&x_2
\end{array}\)](https://www.schullv.de/resources/formulas/e7763e6856b7c9868125663ea44b40682db7485f26db3b4986b65284ca2ce8df_light.svg)
Bei

liegt also ein
Minimum vor. Bestimme zuletzt die vollständigen Koordinaten des Tiefpunkts

:
![\(\begin{array}[t]{rll}
f(x_2)&=& \left(\frac{3}{2}\right)^4 - 2 \cdot \left(\frac{3}{2}\right)^3 = \frac{81}{16} - \frac{27}{4} = -\frac{27}{16} = -1,6875\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d05d5be554d055b7b29f1b14982f4361f16fff0cd4cc74d9664be3780ce9a653_light.svg)

besitzt einen Tiefpunkt

mit den Koordinaten

c)
 Zeichnen des Graphen von
Zeichnen des Graphen von  und der Geraden
und der Geraden 
Gerade

schneidet

im Wendepunkt

und dem Punkt

mit den Koordinaten

. Deine Aufgabe ist es nun, beide in ein
gemeinsames Schaubild zu übertragen.
Das weißt du bereits über die zu zeichnenden Graphen:
Das Schaubild sollte hier wie folgt aussehen:
 Angeben der Gleichung der Geraden
Angeben der Gleichung der Geraden 
Des weitern sollst du hier die Gleichung der Geraden

angeben. Die Grundform einer Geradengleichung lautet dabei:
Die Steigung

der Geraden kannst du dabei über diesen Zusammenhang bestimmen:
Den

-Achsenabschnitt

bestimmst du anschließend über eine
Punktprobe mit

oder

.
1. Schritt: Bestimmen der Steigung 
Setze

und

in die Formel für

ein und berechne so:
![\(\begin{array}[t]{rll}
m&=& \dfrac{0 - (-1)}{2 - 1} = \dfrac{1}{1} = 1\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f24b5cf3a8e56ccfeb041669fd2d1d1ba3103b986023f75bde83ad8666b2fbd3_light.svg) 2. Schritt: Bestimmen des
2. Schritt: Bestimmen des  -Achsenabschnitts
-Achsenabschnitts 
Führe bspw. eine Punktprobe mit

durch, um den

-Achsenabschnitt zu bestimmen:
![\(\begin{array}[t]{rll}
g(1)&=& -1\\[5pt]
-1&=& 1 + b\;\Leftrightarrow\; b = -2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/55ffd59d7048335b6996733c0fb8377e73bc9a453ea6bfe5f72fa92c89f2b7d3_light.svg)
Die Geradengleichung der Geraden

lautet also:

.
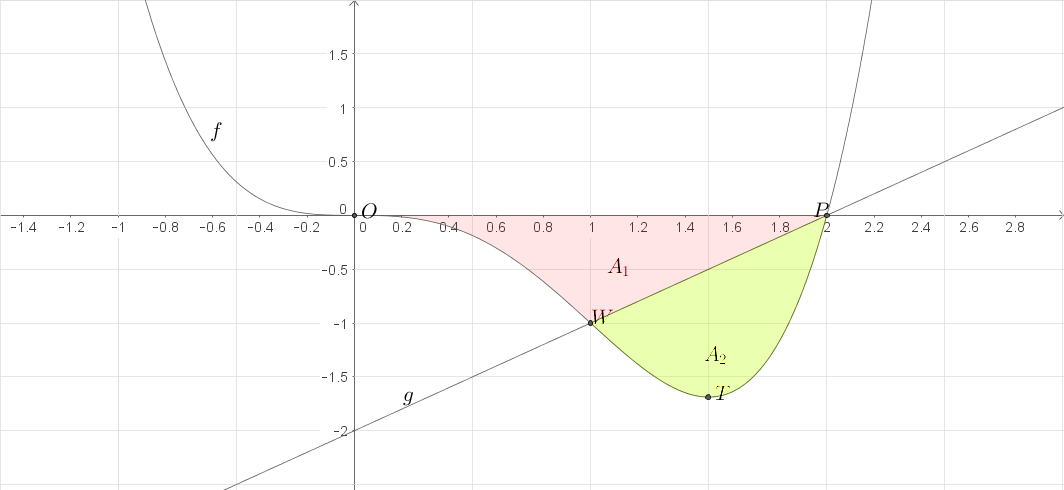
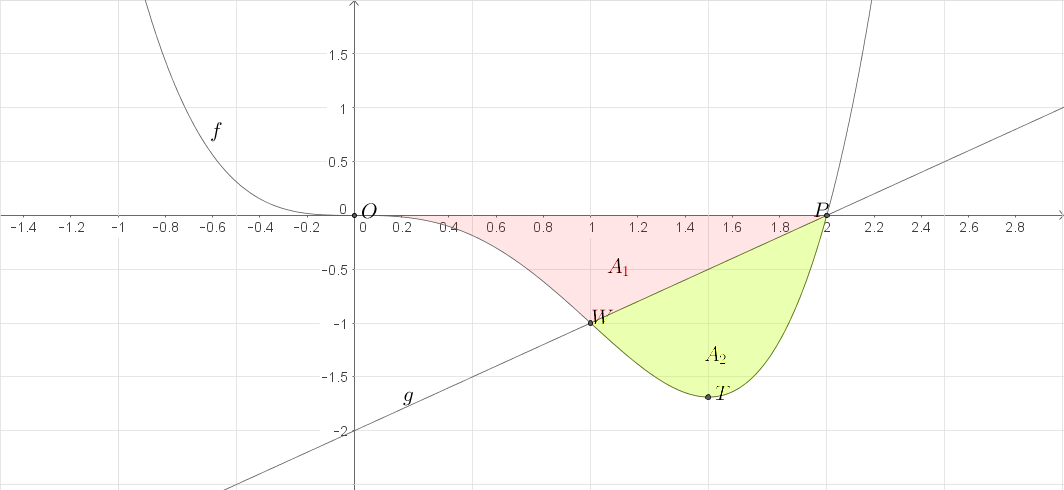
d)
 Berechnen des Verhältnisses der Flächeninhalte der Teilflächen
Berechnen des Verhältnisses der Flächeninhalte der Teilflächen
Der Aufgabenstellung kannst du nun entnehmen, dass

und die

-Achse im IV-Quadranten ein Flächenstück einschließen, das durch die Gerade

in
zwei Teilflächen zerlegt wird. Deine Aufgabe ist es nun, das
Verhältnis der Flächeninhalte dieser beiden Teilflächen zu berechnen.
Fertige dir dazu eine Skizze zum Sachverhalt an. Ergänze dazu das Schaubild aus c.
Im Schaubild kannst du erkennen, dass sich Flächenstück

über das
Integral über
 vom Ursprung bis zum Schnittpunkt
vom Ursprung bis zum Schnittpunkt 
und das Integral über

von der
Schnittstelle bis zur Nullstelle bei 
ergibt. Letztere Fläche bildet ein
rechtwinkliges Dreieck.
Fläche

ergibt sich über ein Integral über

. Integriere dazu
zwischen  und
und 
. Vergiss nicht hiervon noch die Fläche zwischen

und der

-Achse zu subtrahieren.
1. Schritt: Flächenstück 
Berechne zunächst die Fläche zwischen der

-Achse und

, indem du über

innerhalb der Grenzen

und

integrierst. Vergiss dabei nicht den
Betrag deines Ergebnisses zu bilden.
![\(\begin{array}[t]{rll}
A_1‘&=& \left|\displaystyle\int_{x_O}^{x_W}f(x)\;\mathrm dx\right| = \left|\displaystyle\int_{0}^{1}\left(x^4-2\cdot x^3\right)\;\mathrm dx \right|= \left|\left[\frac{1}{5} \cdot x^5 - \frac{1}{2} \cdot x^4\right]_0^1\right|\\[5pt]
&=&\left|\left(\frac{1}{5} \cdot 1^5 - \frac{1}{2} \cdot 1^4\right) - \left(\frac{1}{5} \cdot 0^5 - \frac{1}{2} \cdot 0^4\right)\right|\\[5pt]
&=&\left|\frac{1}{5} - \frac{1}{2}\right| = \frac{3}{10}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/146ac669af912a8a7fef07bffc8769ec15aef1c5eade11835759bbb4c8b5213f_light.svg)
Wie oben schon erwähnt bildet Gerade

mit der

-Achse ein
rechtwinkliges Dreieck. Dieses Dreieck besitzt dabei die Grundseite mit der Länge

und eine Höhe von

:

Der Flächeninhalt

ergibt sich also zu:
 2. Schritt: Flächenstück
2. Schritt: Flächenstück 
Berechne nun das Integral über

im Intervall

und

. Subtrahiere anschließend den Flächeninhalt des rechtwinkligen Dreiecks.
![\(\begin{array}[t]{rll}
A_2‘&=& \left|\displaystyle\int_{x_W}^{x_P}f(x)\;\mathrm dx\right| = \left|\displaystyle\int_{1}^{2}\left(x^4-2\cdot x^3\right)\;\mathrm dx \right|= \left|\left[\frac{1}{5} \cdot x^5 - \frac{1}{2} \cdot x^4\right]_1^2\right|\\[5pt]
&=&\left|\left(\frac{1}{5} \cdot 2^5 - \frac{1}{2} \cdot 2^4\right) - \left(\frac{1}{5} \cdot 1^5 - \frac{1}{2} \cdot 1^4\right)\right|\\[5pt]
&=&\left|\left(\frac{32}{5} - \frac{16}{2}\right)-\left(\frac{1}{5} - \frac{1}{2}\right)\right| = \left|-\frac{8}{5} +\frac{3}{10}\right|= \frac{13}{10} = 1,3\,\text{FE}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4c0c12ba1ef5ee52f2bb44c01aa8ad200613da7a14dc5d6b7516e5d8f1acf1c0_light.svg)
Der Flächeninhalt

ergibt sich nun über folgende Differenz:

Das Verhältnis beider Flächeninhalte zueinander ist nun:

Das Verhältnis beider Teilflächen zueinander ist 1.
a)
 Zuordnen der Graphen und Begründen
Zuordnen der Graphen und Begründen
Hier hast du die Funktion

mit

sowie die Funktionenschar

mit

gegeben. Weiterhin sind die die Graphen in den Abbildungen 1 bis 4 gegeben.
Hier ist es deine Aufgabe diese Graphen den Funktionen

,

,

und

zuzuordnen, wobei du bei drei Zuordnungen diese mittels Aussagen zur
Symmetrie, den Schnittpunkten mit den Koordinatenachsen oder dem
Verhalten der Funktion an den
Grenzen des Definitionsbereichs begründen.
Bestimme dazu zunächst die fehlenden Funktionsterme:
Betrachte nun jede Funktion einzeln und treffe Aussagen über Symmetrie, Schnittpunkte mit den Koordinatenachsen oder Grenzwertverhalten. Beachte dabei, dass eine ganzrationale Funktion
achsensymmetrisch ist, wenn diese
nur gerade Exponenten besitzt. Besitzt sie wiederum
nur ungerade Exponenten, so ist sie
punktsymmetrisch.
1. Funktion 
Funktion

ist offensichtlich
achsensymmetrisch. Berechne nun den Schnittpunkt mit der

-Achse, um weitere Aussagen treffen zu können:

Du erkennst sofort, Funktion

gehört zum Schaubild in Abbildung 4.
2. Funktion 
Betrachtest du den Funktionsterm von

näher, so kannst du erkennen, dass der Graph von
 weder punkt- noch achsensymmetrisch
weder punkt- noch achsensymmetrisch sein kann. Betrachtest du die gegebenen Abbildungen näher, so siehst du, dass

eindeutig dem Schaubild in Abbildung 3 zugeordnet werden kann.
3. Funktion  und
und 
Betrachtest du den Funktionsterm von

näher, so kannst du erkennen, dass diese Funktion ausschließlich Funktionswerte
kleiner gleich Null besitzt. Diese beschreibt also das Schaubild, welches in Abbildung 2 dargestellt wird.
Funktion

kann also nach dem Ausschlussverfahren dem Schaubild in Abbildung 1 zugeordnet werden.
b)
 Angeben des Verhaltens für
Angeben des Verhaltens für 
Betrachtet werden nun die Funktionen

für

. Deine Aufgabe ist es nun, dass Verhalten dieser Funktionen für

in Abhängigkeit von

zu bestimmen.
Hier musst du also eine
Grenzwertbetrachtung durchführen. Beachte dabei, dass jenes

mit dem
größeren Exponenten auch ein
stärkeres Wachstum für

besitzt. Denke des weiteren daran zwischen geraden und ungeraden
 zu unterscheiden
zu unterscheiden.
1. Schritt: Grenzwertverhalten für 
Berechne zunächst den allgemeinen Grenzwert für

. Beachte dabei, da

gilt, bestimmt der variable Teil im Funktionsterm das Grenzwertverhalten.

Betrachtest du den Term nun näher, so kannst du erkennen, dass der hintere Teil,
unabhängig vom Vorzeichen von

, gegen

strebt. Für den Grenzwert gilt also:
 2. Schritt: Grenzwertverhalten für
2. Schritt: Grenzwertverhalten für 
Gehe wie oben vor und berechne zunächst allgemein den Grenzwert, bevor du zwischen geradem und ungeradem

unterscheidest:

Besitzt

einen
geraden Wert, so werden alle mit

potenzierte
 positiv
positiv. Der Term strebt für

also gegen

:

gerade:\;

Besitzt

einen
ungeraden Wert, so werden alle mit

potenzierte
 negativ
negativ. Der Term wird positiv und strebt für

also gegen

:

ungerade:\;

a)
 Berechnen von
Berechnen von  und Interpretieren im Zusammenhang
und Interpretieren im Zusammenhang
Der Aufgabenstellung kannst du entnehmen, dass

, mit
die Atemstromstärke einer ruhenden Testperson in Abhängigkeit von

in Sekunden wiedergibt. Der Aufgabenstellung kannst du entnehmen, dass der Wert der Atemstromstärke beim Einatmen
positiv ist. Beachte dies beim Interpretieren des Vorzeichens des berechneten Funktionswertes.
Setze nun

in

ein und berechne wie folgt:

Das Vorzeichen des Funktionswertes verrät dir, dass die betrachtete Versuchsperson nach 1,5

Sekunden
ausatmet. Sie atmet dabei mit einer Atemstromstärke von 0,278

Liter.
b)
 Angeben eines Zeitpunkts, zudem das Luftvolumen in der Lunge minimal ist
Angeben eines Zeitpunkts, zudem das Luftvolumen in der Lunge minimal ist
Der Aufgabenstellung kannst du entnehmen, dass der Graph von

die
momentane Änderungsrate des Luftvolumens in der Lunge angibt.
Für eine Stammfunktion von

bedeutet dies, dass diese zwangsläufig das
Luftvolumen zu jedem Zeitpunkt

in

angeben muss. Weiterhin kannst du folgern, dass das Luftvolumen bei den Nullstellen von

Extremstellen besitzen muss.
Führe dir also nochmal vor Augen, was für eine
Minimalstelle gelten muss und begründe mit Hilfe der gegebenen Abbildung.
Dort wo

eine Nullstelle mit Vorzeichenwechsel von

nach

besitzt, besitzt das Luftvolumen in der Lunge der Testperson ein Minimum. Das heißt, dass das Luftvolumen in der Lunge Testperson beispielsweise zum Zeitpunkt

einen minimalen Wert annimmt.
c)
 Berechnen des Integrals und begründen im Zusammenhang
Berechnen des Integrals und begründen im Zusammenhang
Hier sollst du nun das Integral

berechnen und den Wert dieses Integrals im Sachzusammenhang deuten. Beachte dabei, dass

die
momentane Änderungsrate des Luftvolumens in der Lunge der Testperson angibt.
Für eine Stammfunktion

bedeutet das, dass diese das momentane Volumen der Luft in Litern in der Lunge der Testperson angibt. Betrachte beim Interpretieren des Wertes im Zusammenhang auch die gegebene Abbildung von

.
Beachte beim Bestimmen der Stammfunktion

von

das folgender Zusammenhang gilt:
1. Schritt: Berechnen des Integralwertes
![\(\begin{array}[t]{rll}
I&=& \displaystyle\int_{2}^{4}g(t)\;\mathrm dt = \displaystyle\int_{2}^{4}\left(\frac{-\pi}{8} \cdot \sin \left(\dfrac{\pi}{2} \cdot t\right)\right) = \left[ \dfrac{1}{4}\cdot\cos\left(\dfrac{\pi}{2} \cdot t\right)\right]_2^4\\[5pt]
&=& \left(\dfrac{1}{4}\cdot\cos\left(\dfrac{\pi}{2} \cdot 4\right)\right) - \left( \dfrac{1}{4}\cdot\cos\left(\dfrac{\pi}{2} \cdot 2\right)\right)\\[5pt]
&=&\left(\dfrac{1}{4}\cdot\cos\left(2 \cdot \pi \right)\right) - \left( \dfrac{1}{4}\cdot\cos\left(\pi \right)\right)\\[5pt]
&=&\dfrac{1}{4} - \left(-\dfrac{1}{4}\right) = \dfrac{1}{2} = 0,5\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/aa45a049a931645112312871773ca5f226b6d7325725e080c0c59957cf89d476_light.svg) 2. Schritt: Interpretieren im Sachzusammenhang
2. Schritt: Interpretieren im Sachzusammenhang
Der Wert des Integrals ist

. Das heißt, die betrachtete Testperson hat im Zeitraum zwischen 2 und 4 Sekunden insgesamt 0,5

Luft eingeatmet.
d)
 Skizzieren des Graphens der Stammfunktion
Skizzieren des Graphens der Stammfunktion
Der Aufgabenstellung kannst du entnehmen, dass sich zu Beginn eines Ausatemvorgangs insgesamt 3,5

Luft in der Lunge der Testperson befindet. Auf dieser Grundlage sollst du nun den Verlauf des Luftvolumens für

zeichnen.
Oben hast du bereits eine Stammfunktion

von

bestimmt. Diese gilt es in ein Schaubild für

zu zeichnen. Beachte dabei, dass

gelten muss und das es sich um eine
gestauchte Kosinusfunktion mit einer
Periode von 
handelt.
Das hier zu zeichnende Schaubild muss also wie folgt aussehen:
e)
 Angeben der Atemfrequenz der Testperson
Angeben der Atemfrequenz der Testperson
Der Aufgabenstellung kannst du entnehmen, dass die Testperson für einen vollständigen Atemzyklus insgesamt 4 Sekunden benötigt. Deine Aufgabe ist es zunächst, die Atemfrequenz der Testperson anzugeben.
Der Aufgabenstellung kannst du dazu entnehmen, dass die Atemfrequenz der
Anzahl der Atemzyklen pro Minute entspricht.
Die Atemfrequenz

der Testperson entspricht also folgendem Wert:

Die Atemfrequenz der Testperson entspricht

.
 Ermitteln des Wertes für
Ermitteln des Wertes für 
Nun soll die Atemstromstärke eines jüngeren Menschen, dessen Atemfrequenz um 20

höher ist, durch eine Sinusfunktion der Form
beschrieben werden. Deine Aufgabe ist es dabei, denn Wert des Parameters

zu bestimmen.
Bevor du damit beginnen kannst

zu bestimmen, solltest du dir ins Gedächtnis rufen, was dieser Parameter definiert.

bestimmt die
Periode der Funktion und ist wie folgt definiert:
Leite also aus der Atemfrequenz des jüngeren Menschen die Periode ab und berechne mit dieser den Parameter

.
1. Schritt: Bestimmen der Atemfrequenz der jüngeren Person
Multipliziere die oben berechnete Atemfrequenz

mit 1,2 um die Atemfrequenz

der jüngeren Person zu berechnen:
 2. Schritt: Bestimmen der Parameters
2. Schritt: Bestimmen der Parameters 
Aus den vorherigen Aufgabenteilen weißt du, dass gerade ein Atemzyklus die Periode der Funktion

abbildet. Willst du nun den Parameter

von Funktion

bestimmen, so musst du zunächst ermitteln, wie lange ein Atemzyklus der jüngeren Person dauert.
Teile dazu

durch die Atemfrequenz:
Länge eines Atemzyklus

Bestimme mit diesem Wert nun wie folgt Parameter

:

.
Der hier gesuchte Wert für

beträgt also

.
 mit
mit  und Definitionsbereich:
und Definitionsbereich:
 . Der Graph von
. Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
 zu jedem der drei folgenden Terme äquivalent ist:
zu jedem der drei folgenden Terme äquivalent ist:
 ;
;  ;
; 
 -Achse horizontale Asymptote von
-Achse horizontale Asymptote von  ist, und gib die Gleichungen der vertikalen Asymptoten von
ist, und gib die Gleichungen der vertikalen Asymptoten von  an. Bestimme die Koordinaten des Schnittpunkts von
an. Bestimme die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse.
-Achse.
 mit Definitionsbereich
mit Definitionsbereich ![\(D_h=]-1;+\infty[\)](https://www.schullv.de/resources/formulas/18446c22b501a25051f767bca19781d5252120caa2e7da7f73ed767cc93e8149_light.svg) . Abbildung 2 zeigt den Graphen
. Abbildung 2 zeigt den Graphen  von
von  .
.
besitzt den Schnittpunkt mit der
-Achse:
besitzt die
-Achse als horizontale Asymptote
besitzt die
und
als senkrechte Asymptoten
besitzt einen Hochpunkt, mit
verläuft streng monoton steigend in
verläuft streng monoton fallend in
und
gegeben
ist streng monoton steigend
ist rechtsgekrümmt
entspricht dem Graph der ersten Ableitung des Graphen
ist streng monoton steigend
ist rechtsgekrümmt
und
besitzt eine einzige Nullstelle bei
Minimum
Maximum
. Achtung: Bei
befindet sich eine Wendestelle mit waagrechter Tangente
fest
die vollständigen Koordinaten des Extrempunktes
verläuft durch
und
besitzt einen Wendepunkt mit waagrechter Tangente in
besitzt einen weiteren Wendepunkt bei
besitzt einen Tiefpunkt bei