Teil A
1
2
Gib den Term einer in  definierten Funktion an, deren Graph im Punkt
definierten Funktion an, deren Graph im Punkt  eine waagrechte Tangente, aber keinen Extrempunkt hat.
eine waagrechte Tangente, aber keinen Extrempunkt hat.
(3 BE)
3
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit 
Weise nach, dass folgende Eigenschaften besitzt:
folgende Eigenschaften besitzt:



Weise nach, dass
Der Graph von  besitzt an der Stelle
besitzt an der Stelle  die Steigung
die Steigung 
Der Graph von  besitzt im Punkt
besitzt im Punkt  die
die  -Achse als Tangente.
-Achse als Tangente.
Die Tangente  an den Graphen der Funktion
an den Graphen der Funktion  im Punkt
im Punkt  kann durch die Gleichung
kann durch die Gleichung  beschrieben werden.
beschrieben werden.
(5 BE)
4
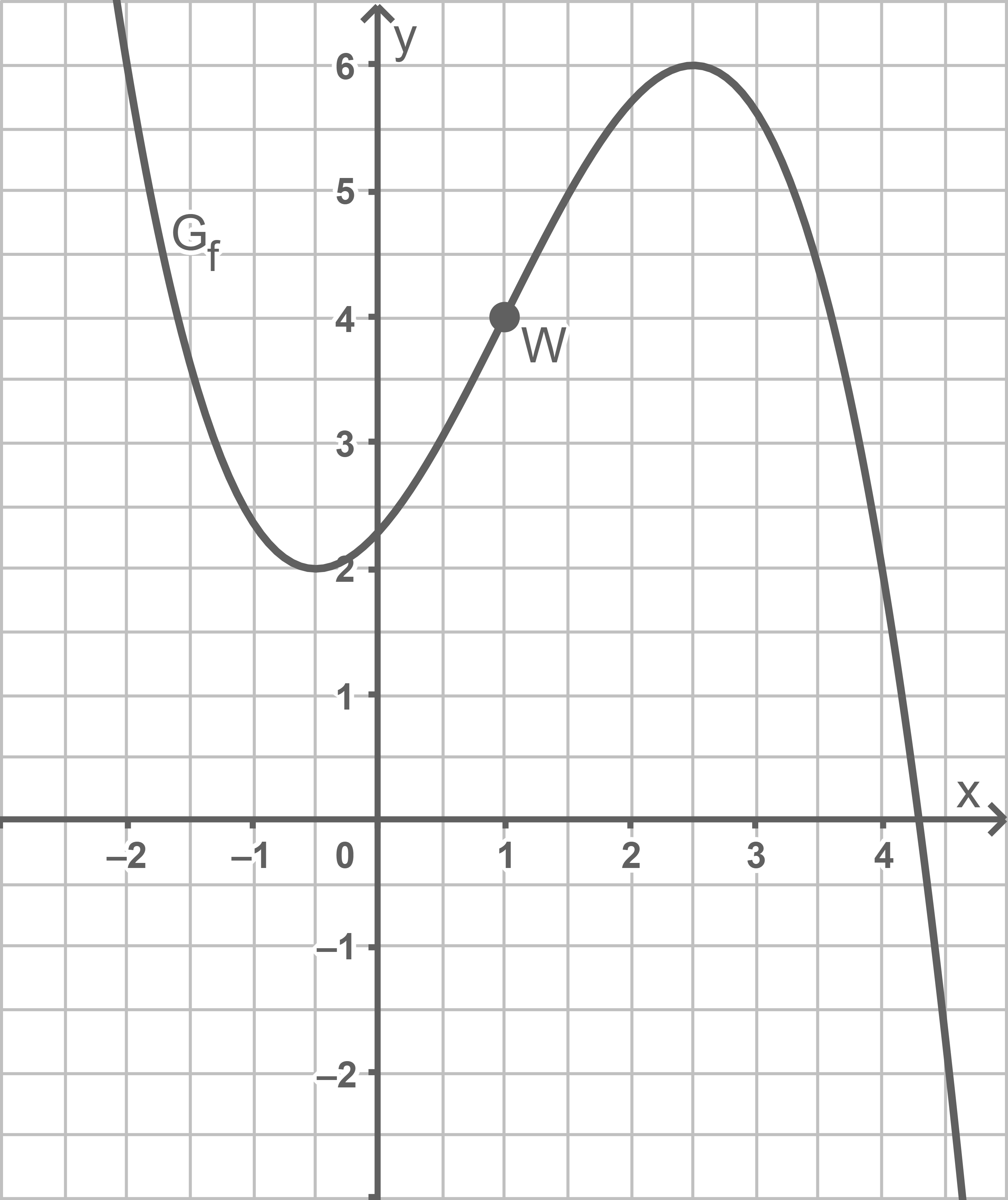
Die Abbildung zeigt den Graphen  einer in
einer in  definierten Funktion
definierten Funktion  mit dem Wendepunkt
mit dem Wendepunkt 
Ermittle mithilfe der Abbildung näherungsweise den Wert der Ableitung von an der Stelle
an der Stelle 
Skizziere den Graphen der Ableitungsfunktion von
von  in die Abbildung; berücksichtige dabei insbesondere die Lage der Nullstellen von
in die Abbildung; berücksichtige dabei insbesondere die Lage der Nullstellen von  sowie den für
sowie den für  ermittelten Näherungswert.
ermittelten Näherungswert.
Ermittle mithilfe der Abbildung näherungsweise den Wert der Ableitung von
Skizziere den Graphen der Ableitungsfunktion
(3 BE)
5
Für jeden Wert von  mit
mit  ist eine Funktion
ist eine Funktion  durch
durch  mit
mit  gegeben.
gegeben.
a)
Eine der beiden Abbildungen stellt einen Graphen von  dar. Gib an, für welche Abbildung dies zutrifft. Begründe deine Antwort.
dar. Gib an, für welche Abbildung dies zutrifft. Begründe deine Antwort.
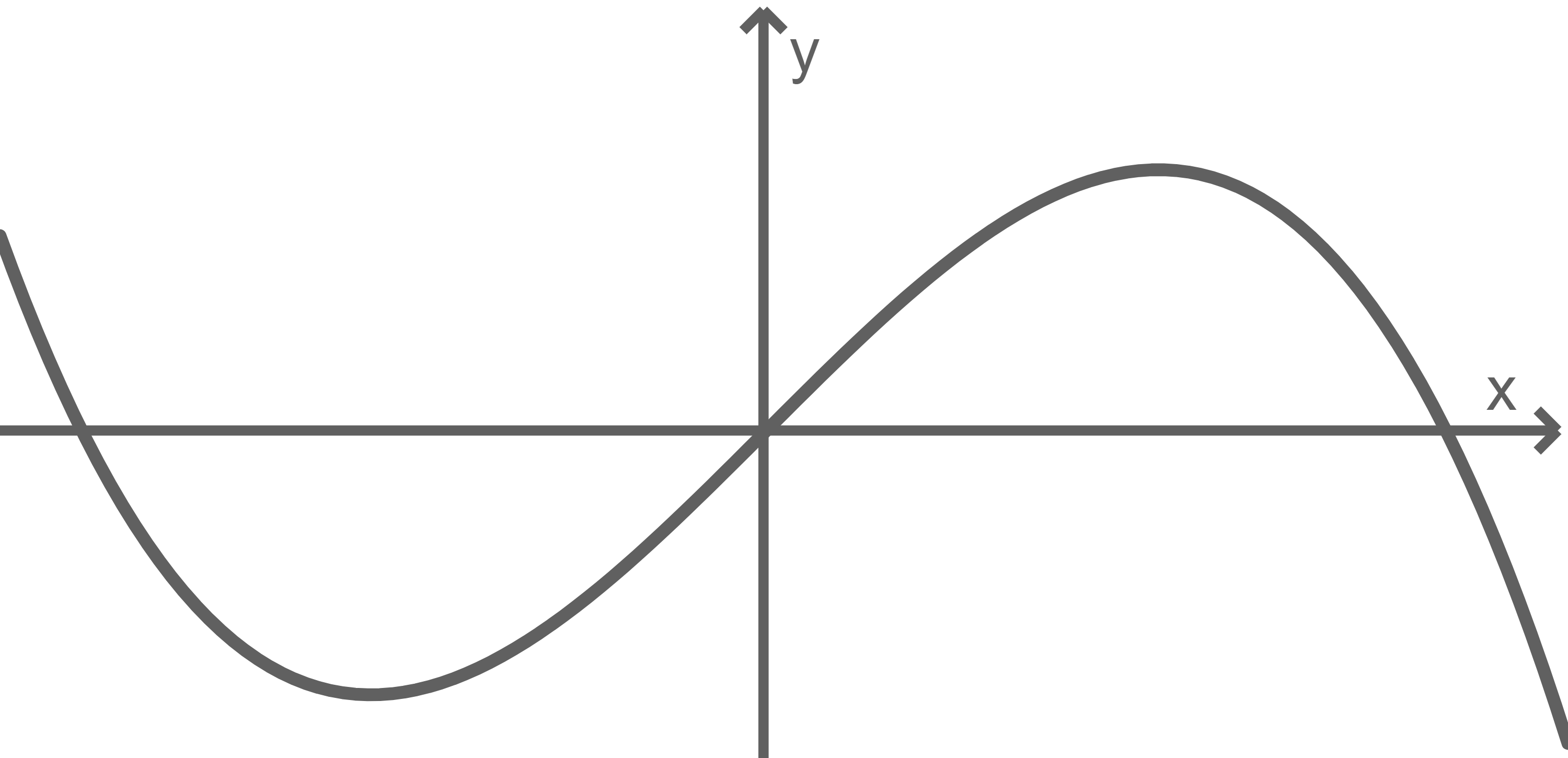
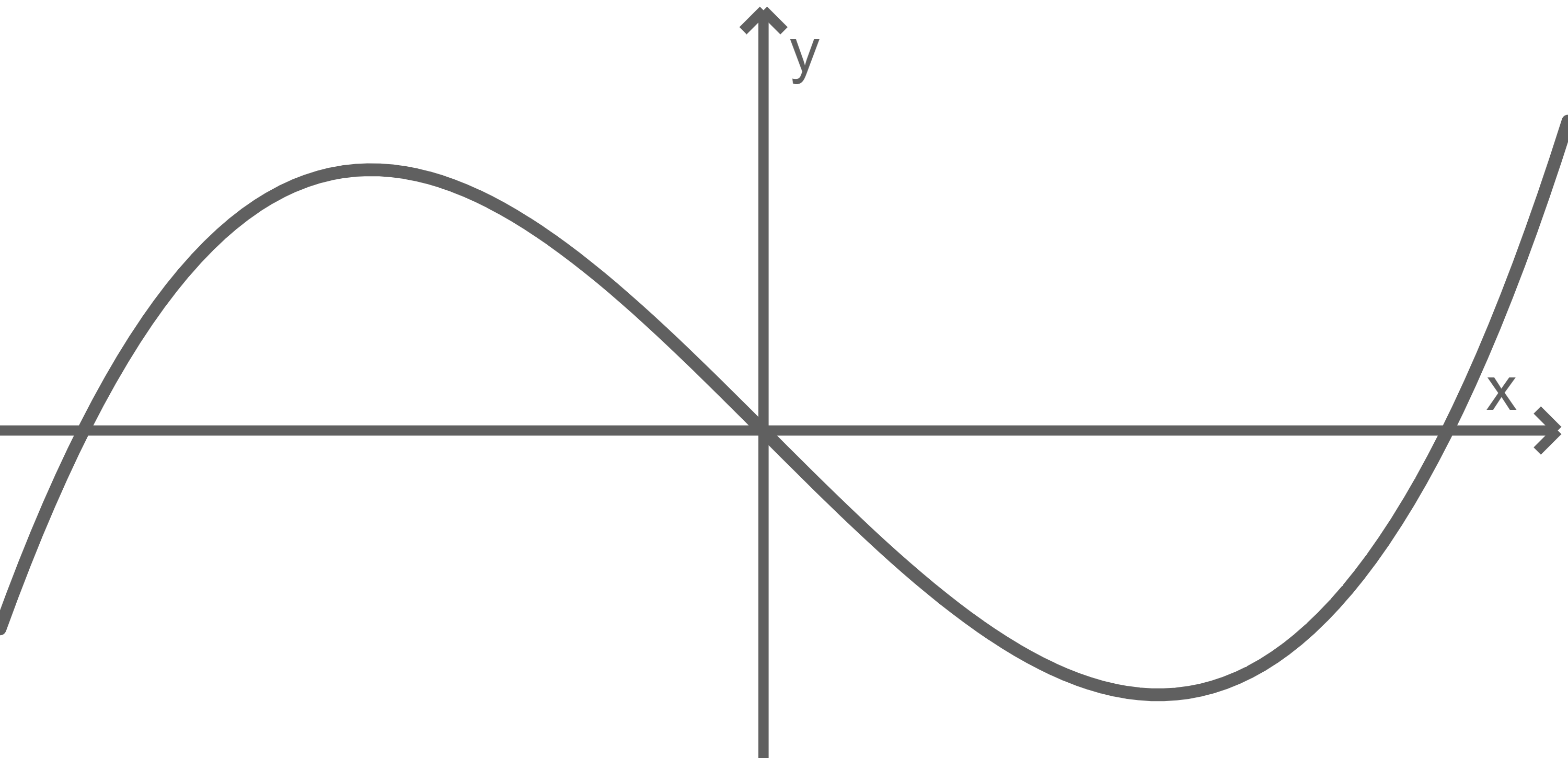

Abb. 1

Abb. 2
(2 BE)
b)
Für jeden Wert von  besitzt der Graph von
besitzt der Graph von  genau zwei Extrempunkte. Ermittle denjenigen Wert von
genau zwei Extrempunkte. Ermittle denjenigen Wert von  für den der Graph der Funktion
für den der Graph der Funktion  an der Stelle
an der Stelle  einen Extrempunkt hat.
einen Extrempunkt hat.
(3 BE)
(20 BE)
1
Definitionsmengen angeben
Für die Nullstellen des Nenners von  folgt:
folgt:
![\(\begin{array}[t]{rll}
x^2-4&=& 0 \\[5pt]
x^2&=& 4 &\quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
x&=& \pm 2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c835e772d6844cfc42c28a1313b0dd7c2274f8073885ef89a0a45b7676442092_light.svg) Der maximale Definitionsbereich von
Der maximale Definitionsbereich von  ergibt sich somit als
ergibt sich somit als  Bei
Bei  muss das Argument des Logarithmus positiv sein:
muss das Argument des Logarithmus positiv sein:
![\(\begin{array}[t]{rll}
x+2&\gt & 0 &\quad \scriptsize \mid\;-2 \\[5pt]
x&\gt & -2
\end{array}\)](https://www.schullv.de/resources/formulas/48b0c7d6945ffaca432fee1f042e0e17c4f522f9745ee003746d0053023c3dfa_light.svg) Der maximale Definitionsbereich von
Der maximale Definitionsbereich von  folgt somit als
folgt somit als ![\(\mathbb{D}_{f_2} =\;]-2;+\infty[.\)](https://www.schullv.de/resources/formulas/9dd5c7526dc269d8058ec057e2805fc61d65be9a403f4806e5604f64f1b1a58a_light.svg) Nullstellen bestimmen
Die Nullstelle von
Nullstellen bestimmen
Die Nullstelle von  ergibt sich als die Nullstelle des Zählers:
ergibt sich als die Nullstelle des Zählers:
![\(\begin{array}[t]{rll}
2x+3&=& 0 &\quad \scriptsize \mid\;-3 \\[5pt]
2x&=& -3 &\quad \scriptsize \mid\;:2 \\[5pt]
x&=& -1,5 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cec2be19630ba7f8a7b4ad86e2a97e101395b79b2a62e2b2d3fbe9d236122eb3_light.svg) Die Logarithmusfunktion
Die Logarithmusfunktion  besitzt die Nullstelle
besitzt die Nullstelle  Somit folgt für die Nullstelle von
Somit folgt für die Nullstelle von 
![\(\begin{array}[t]{rll}
x+2&=& 1 &\quad \scriptsize \mid\;-2 \\[5pt]
x&=& -1
\end{array}\)](https://www.schullv.de/resources/formulas/3f0c0d772ea0a7490ad9b6227de796011cc95bba9caa7806917291ee3bfabfae_light.svg)
2
Ein Punkt mit waagerechter Tangente, der kein Extrempunkt ist, ist ein Sattelpunkt. Die Funktion  besitzt einen Sattelpunkt in
besitzt einen Sattelpunkt in  Durch Verschiebung von
Durch Verschiebung von  um zwei Längeneinheiten in
um zwei Längeneinheiten in  -Richtung und eine Längeneinheit in
-Richtung und eine Längeneinheit in  -Richtung ergibt sich somit eine mögliche Funktion:
-Richtung ergibt sich somit eine mögliche Funktion:
![\(\begin{array}[t]{rll}
g(x)&=& f(x-2) +1 \\[5pt]
&=& (x-2)^3 +1
\end{array}\)](https://www.schullv.de/resources/formulas/21838289ed7f4ce939774c902c8bdfb80acadf4e20560994e19d11baf868ab20_light.svg) Der Term einer in
Der Term einer in  definierten Funktion, deren Graph im Punkt
definierten Funktion, deren Graph im Punkt  eine waagerechte Tangente, aber keinen Extrempunkt besitzt, ist somit beispielsweise gegeben durch
eine waagerechte Tangente, aber keinen Extrempunkt besitzt, ist somit beispielsweise gegeben durch 
3
Ableiten von  liefert:
liefert:




Steigung
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/dd069879cf3fe1e50757b1c2f4e3fcb7474f2da78b917e29ece644b5cfab865c_light.svg) Der Graph von
Der Graph von  besitzt somit an der Stelle
besitzt somit an der Stelle  die Steigung
die Steigung 
Tangente
![\(\begin{array}[t]{rll}
f(5)&=& -5^3+9\cdot 5^2 -15\cdot 5 -25 \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/0d02e25b235d5c5e4cb5bdd735509f210cc6f5e1edcde6440339eaaa501836d8_light.svg)
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/91789a8bb09dbe7bbd679cbf003ddbe1de70e552742ef5291231f6a206aa1aa8_light.svg) Die
Die  -Achse mit der Gleichung
-Achse mit der Gleichung  ist somit eine Tangente an den Graphen von
ist somit eine Tangente an den Graphen von  im Punkt
im Punkt 
Tangente
Die Gerade mit der Gleichung  besitzt die Steigung
besitzt die Steigung  Für die Steigung des Graphen von
Für die Steigung des Graphen von  im Punkt
im Punkt  gilt:
Für die Funktionswerte der beiden Funktionen an der Stelle
gilt:
Für die Funktionswerte der beiden Funktionen an der Stelle  folgt:
folgt:
![\(\begin{array}[t]{rll}
y&=& -36\cdot (-1) -36 \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/934b3acb70e046ef953de8f630e9c58f5918ee4676ed56bcf28bc8ff652f82bf_light.svg) Da sowohl die beiden Steigungen, als auch die beiden Funktionswerte im Punkt
Da sowohl die beiden Steigungen, als auch die beiden Funktionswerte im Punkt  übereinstimmen, kann die Tangente an den Graphen von
übereinstimmen, kann die Tangente an den Graphen von  im Punkt
im Punkt  durch
durch  beschrieben werden.
beschrieben werden.
4
Ableitungswert bestimmen
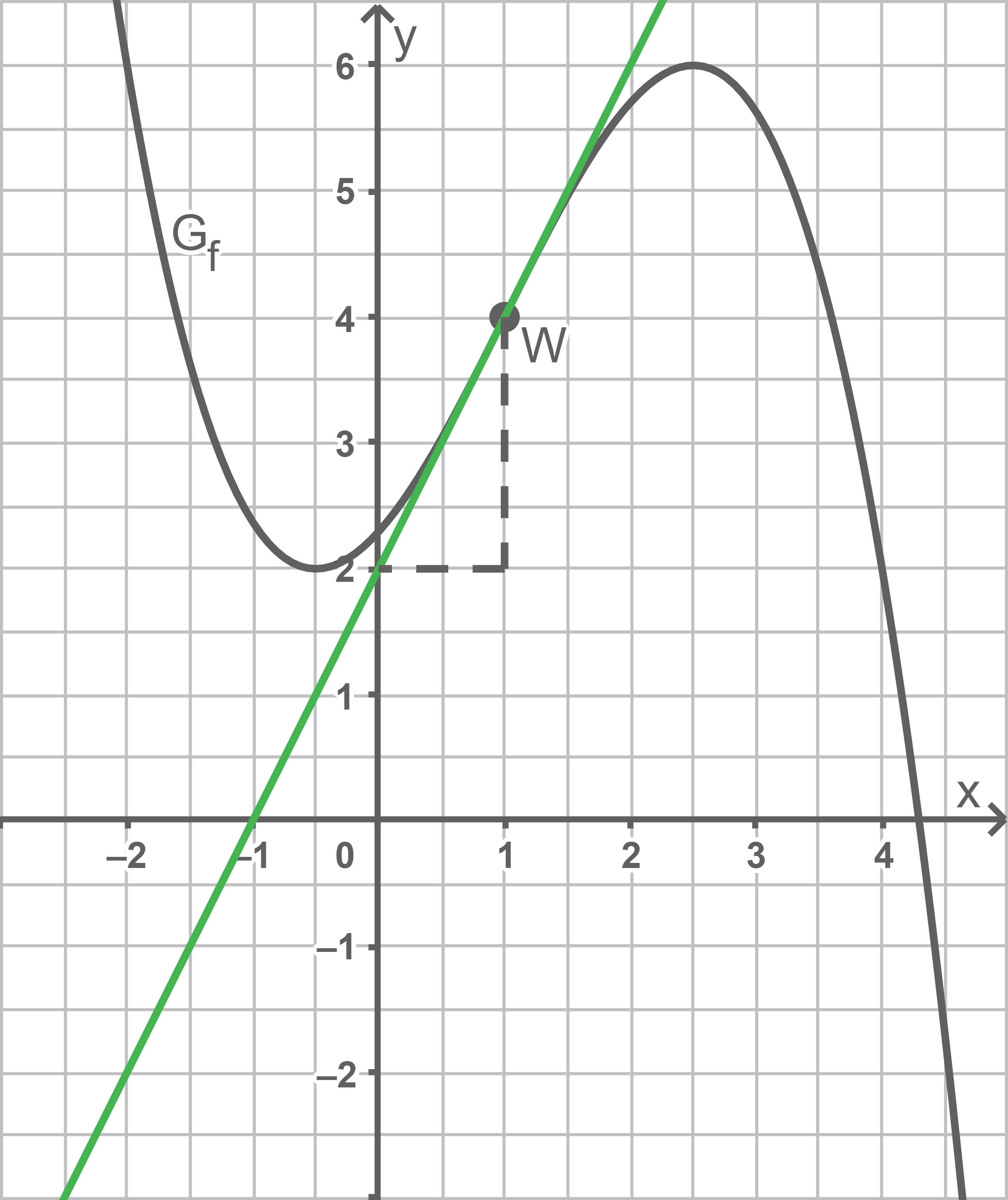 Graphen skizzieren
Graphen skizzieren
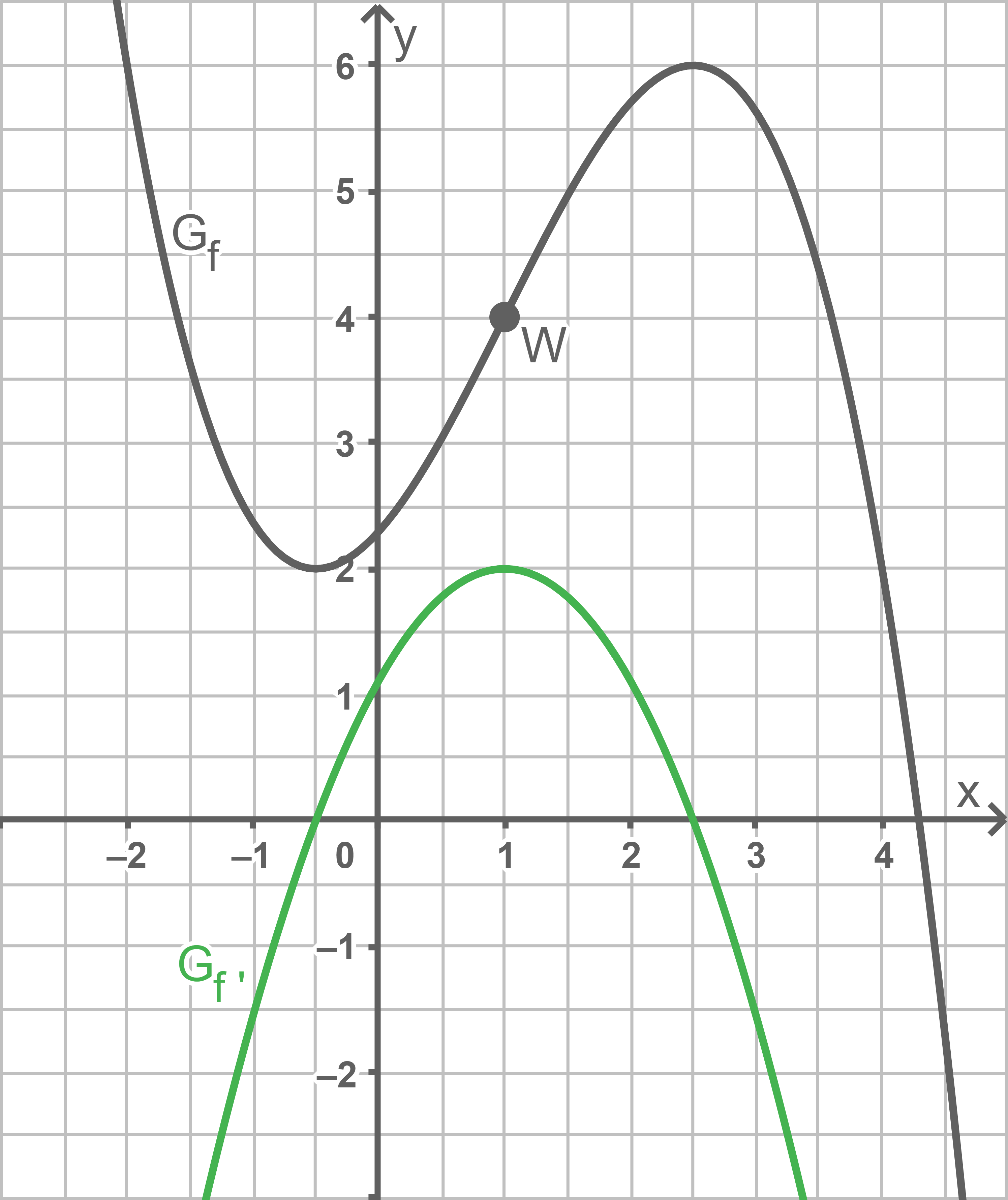
Der Wert der Ableitung von  an der Stelle
an der Stelle  entspricht der Steigung der Tangente an den Graphen von
entspricht der Steigung der Tangente an den Graphen von  an dieser Stelle. Einzeichnen dieser in die Abbildung und Bestimmung der Steigung mit Hilfe eines Steigungsdreiecks liefert für den gesuchten Wert:
an dieser Stelle. Einzeichnen dieser in die Abbildung und Bestimmung der Steigung mit Hilfe eines Steigungsdreiecks liefert für den gesuchten Wert:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/5183d87141dfae2f2e9475ce609ec98201bac2223344a1a04433dc9f4b790758_light.svg)


5
a)
Da  eine positive reelle Zahl ist, folgt:
eine positive reelle Zahl ist, folgt:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to +\infty}f_a(x)&=& \lim\limits_{x\to +\infty}\left(\frac{1}{a}\cdot x^3-x \right) \\[5pt]
&=& +\infty
\end{array}\)](https://www.schullv.de/resources/formulas/4bb2630ccaf90d0de2a42e167d540be34f2d8fc10f9cf8a7e0006448ac5130a0_light.svg) Somit stellt Abbildung 2 den Graph von
Somit stellt Abbildung 2 den Graph von  dar.
dar.
b)
Da die Ableitung von  eine quadratische Funktion ist und somit maximal zwei Nullstellen besitzt, muss nur die notwendige Bedingung überprüft werden. Für die Ableitung von
eine quadratische Funktion ist und somit maximal zwei Nullstellen besitzt, muss nur die notwendige Bedingung überprüft werden. Für die Ableitung von  gilt:
gilt:
 Einsetzen von
Einsetzen von  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_a](https://www.schullv.de/resources/formulas/1b30bbdde222091c57ec57fac53f52cdbf7e8c0858f48a682e2e532dcbc273c0_light.svg) Für
Für  besitzt der Graph von
besitzt der Graph von  an der Stelle
an der Stelle  somit einen Extrempunkt.
somit einen Extrempunkt.