Teil A
1
Gegeben ist die Funktion  mit Definitionsbereich
mit Definitionsbereich 
Bestimme Lage und Art des Extrempunkts des Graphen von
Bestimme Lage und Art des Extrempunkts des Graphen von
(5 BE)
2
Gegeben ist die in  definierte Funktion
definierte Funktion  die die Nullstellen
die die Nullstellen  und
und  hat. Abbildung 1 zeigt den Graphen von
hat. Abbildung 1 zeigt den Graphen von  der symmetrisch bezüglich der
der symmetrisch bezüglich der  -Achse ist. Weiterhin ist die Gerade
-Achse ist. Weiterhin ist die Gerade  mit der Gleichung
mit der Gleichung  gegeben.
gegeben.
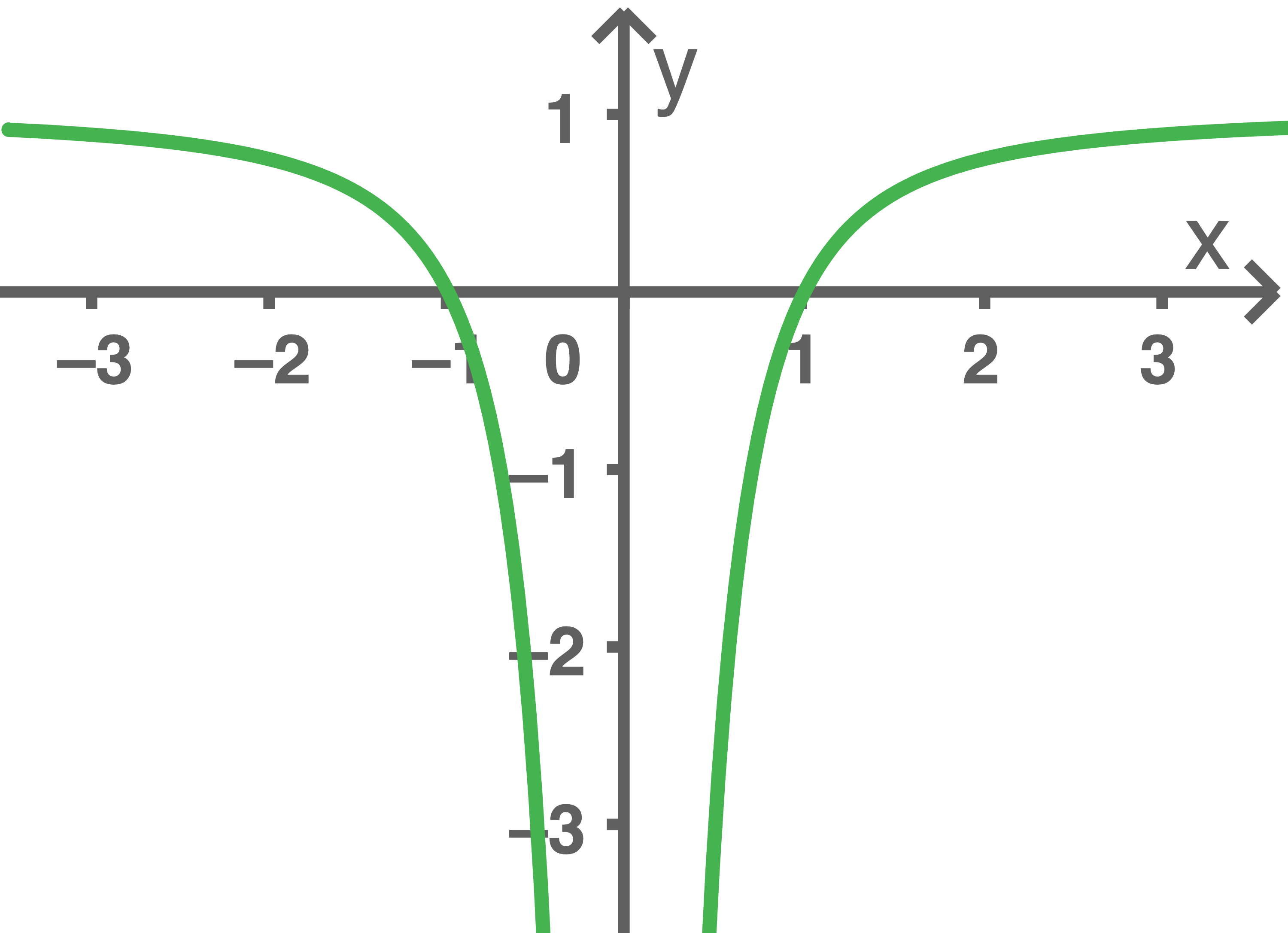
Abb. 1
a)
Zeige, dass einer der Punkte, in denen  den Graphen von
den Graphen von  schneidet, die
schneidet, die  -Koordinate
-Koordinate  hat.
hat.
(1 BE)
b)
Bestimme rechnerisch den Inhalt der Fläche, die der Graph von  die
die  -Achse und die Gerade
-Achse und die Gerade  einschließen.
einschließen.
(4 BE)
3
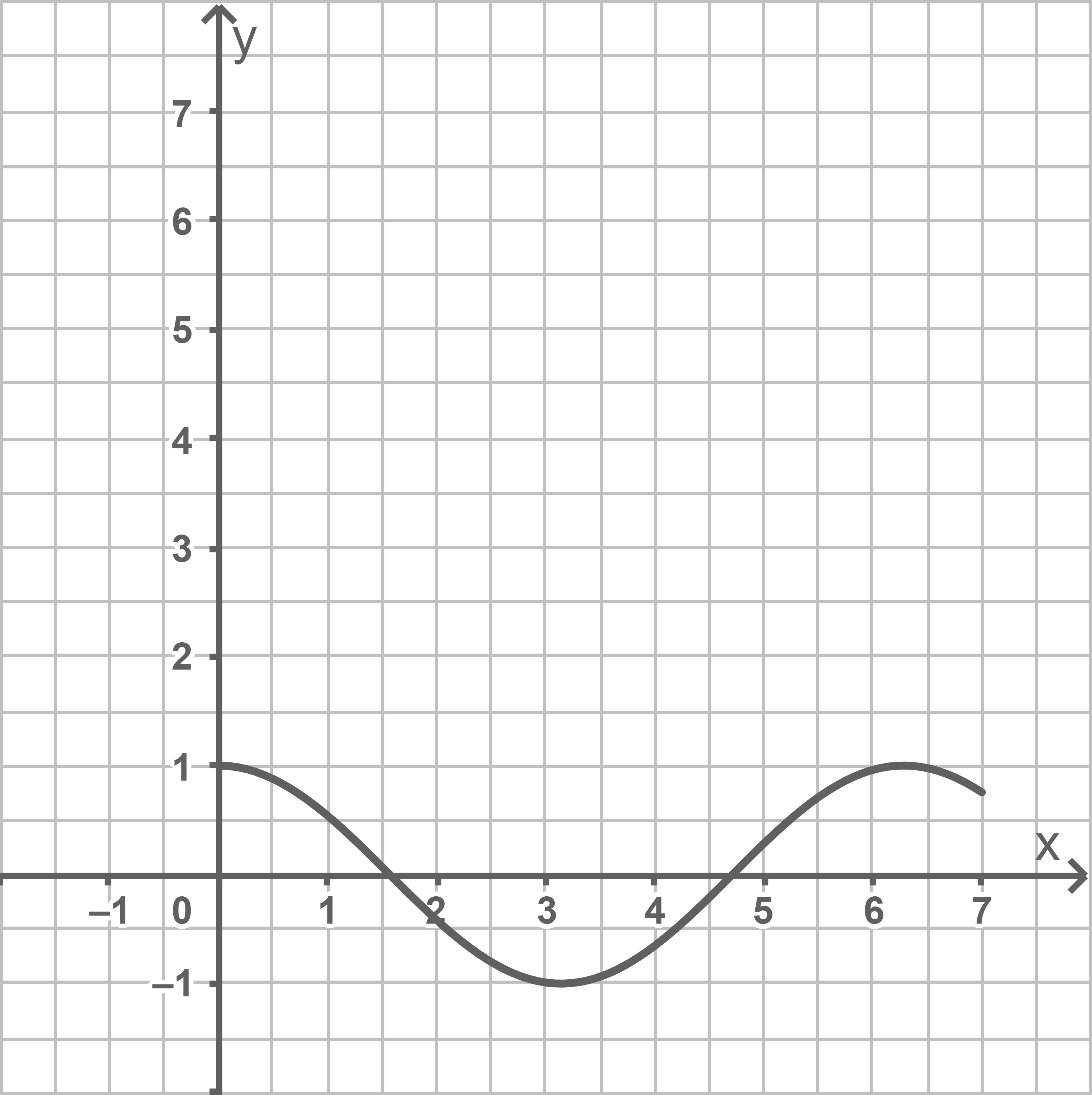
Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion 
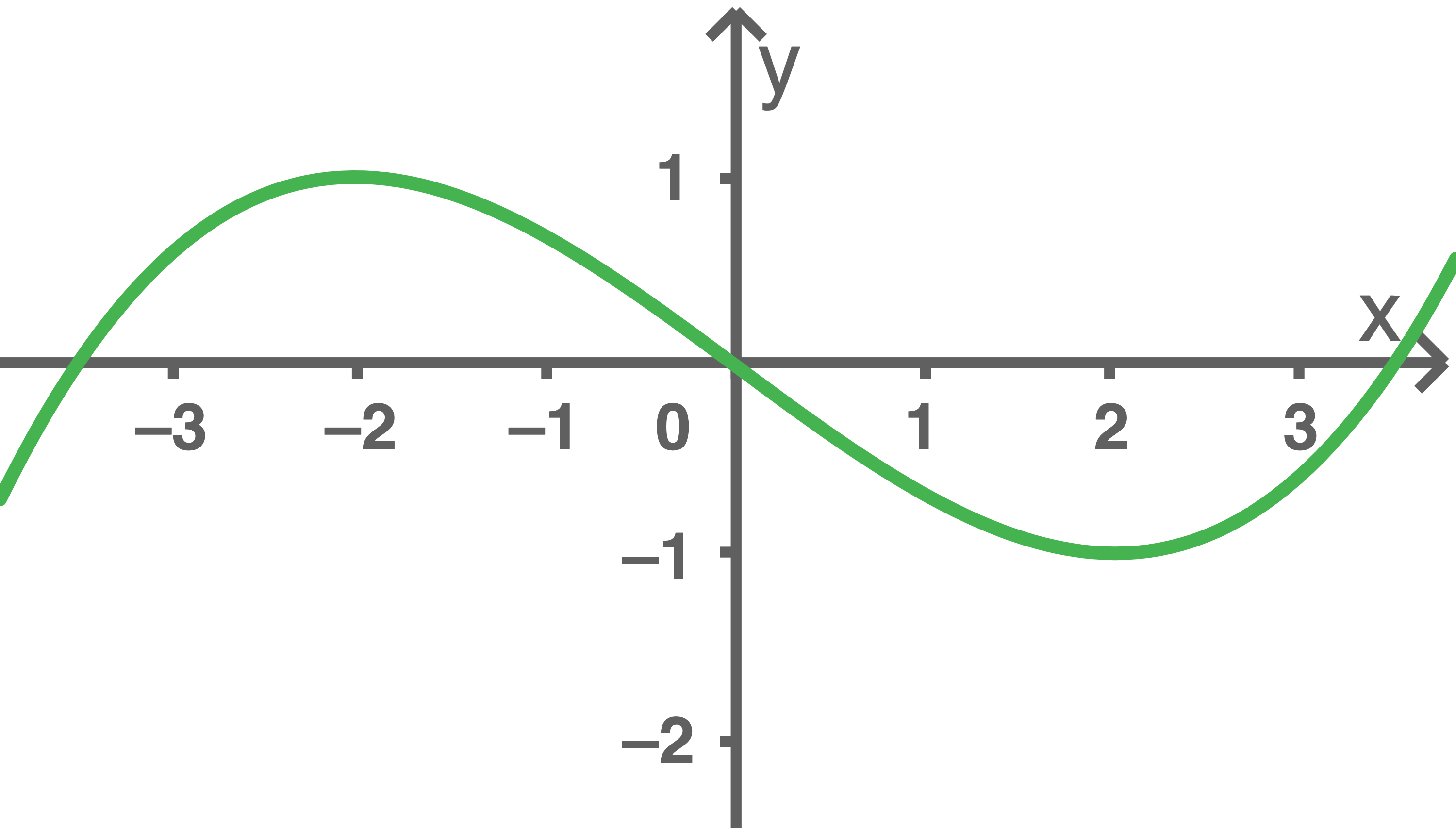
Abb. 2
a)
Einer der folgenden Graphen 
 oder
oder  gehört zur ersten Ableitungsfunktion von
gehört zur ersten Ableitungsfunktion von  Gib diesen Graphen an. Begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.
Gib diesen Graphen an. Begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.
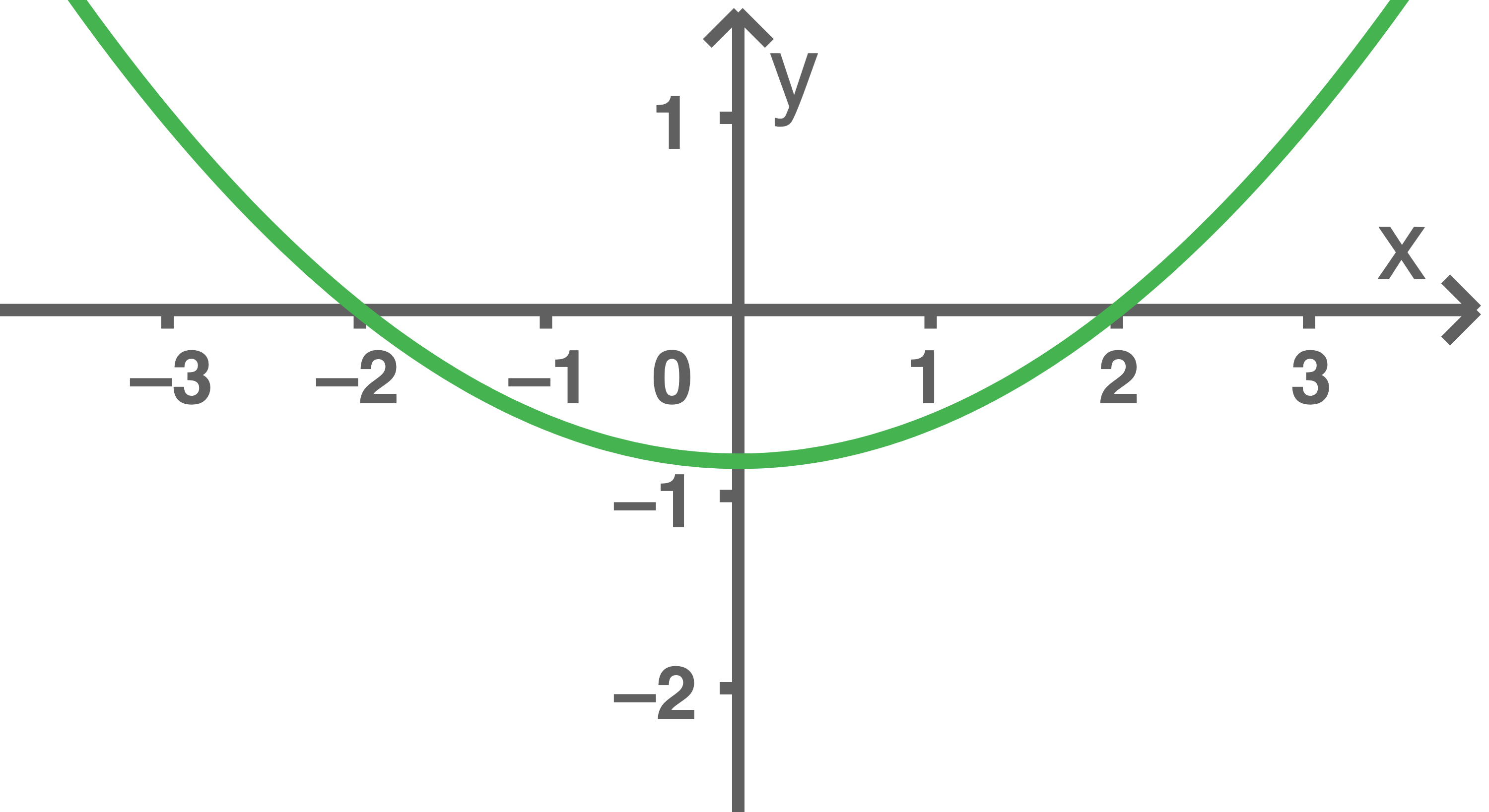
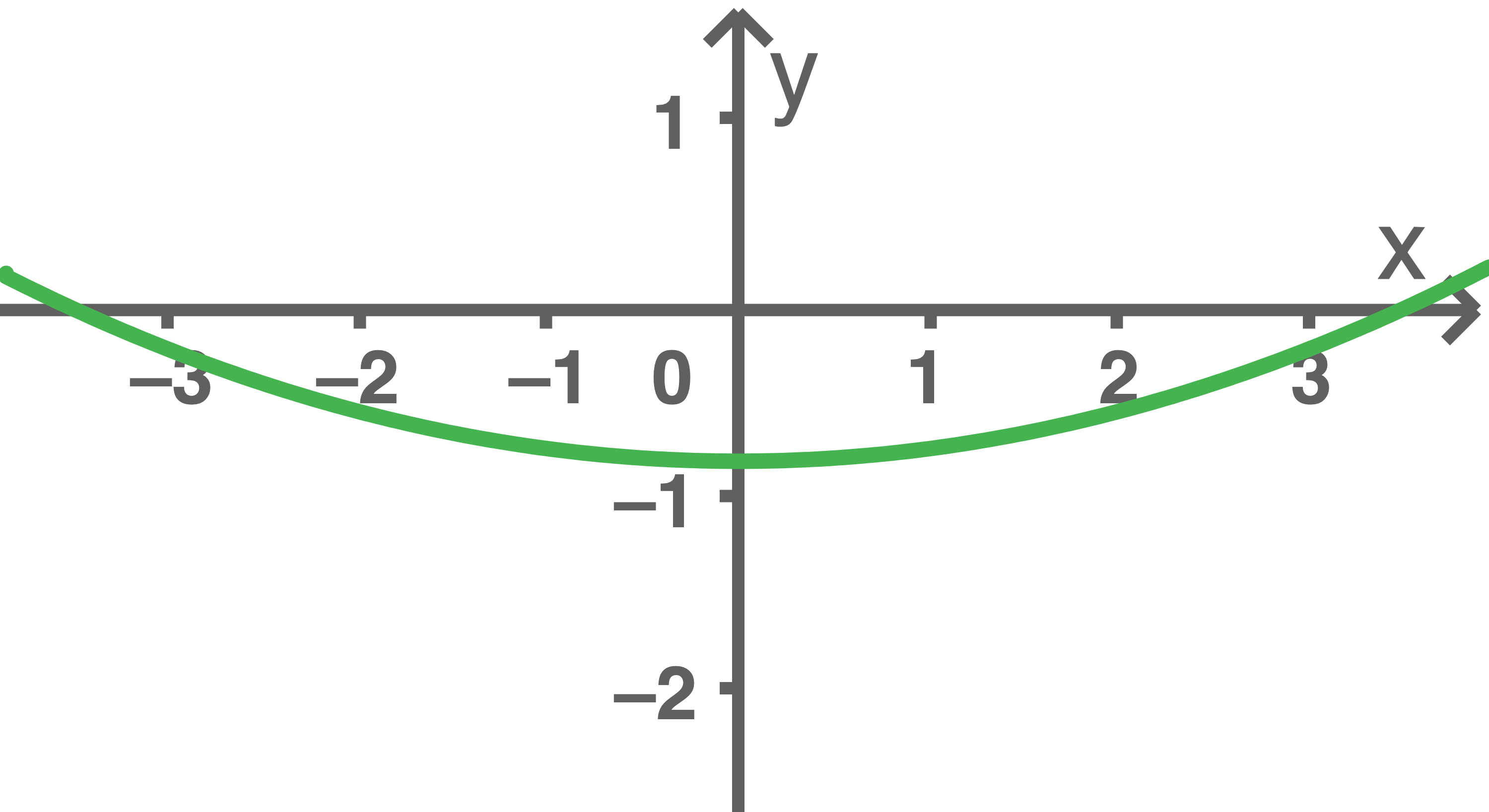
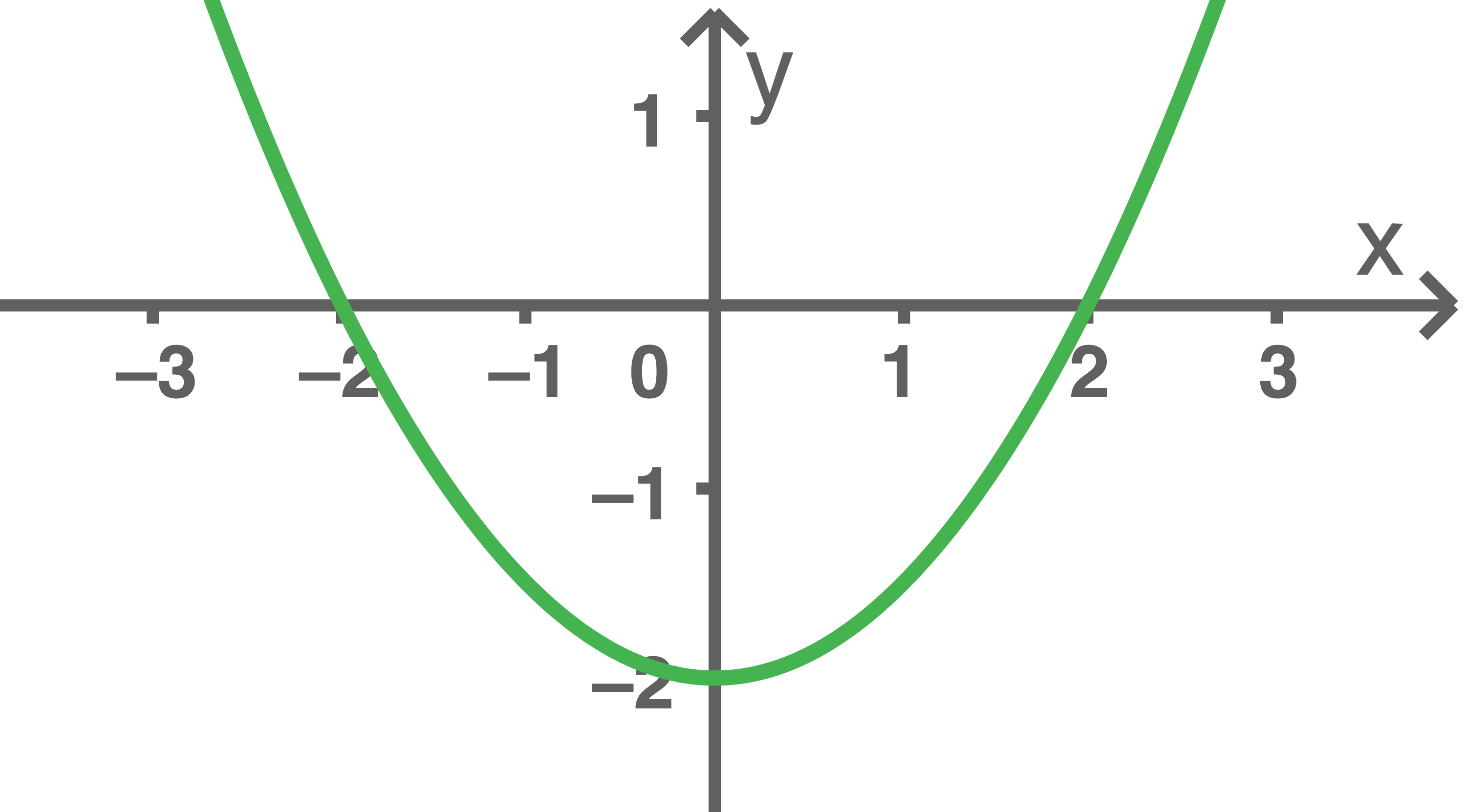



Abb. 3
(3 BE)
b)
Die Funktion  ist eine Stammfunktion von
ist eine Stammfunktion von  Gib das Monotonieverhalten von
Gib das Monotonieverhalten von  im Intervall
im Intervall ![\([1;3]\)](https://www.schullv.de/resources/formulas/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c_light.svg) an. Begründe deine Angabe.
an. Begründe deine Angabe.
(2 BE)
4
a)
Betrachtet wird eine Schar von Funktionen  mit
mit  die sich nur in ihren jeweiligen Definitionsbereichen
die sich nur in ihren jeweiligen Definitionsbereichen  unterscheiden.
unterscheiden.
Es gilt mit
mit ![\(D_k = [0; k].\)](https://www.schullv.de/resources/formulas/582d48c9a68baaeefaefeb0b4534a9daf60610dac9c32a9d1cda92fced11b1eb_light.svg)
Abbildung 4 zeigt den Graphen der Funktion Gib den größtmöglichen Wert von
Gib den größtmöglichen Wert von  an, sodass die zugehörige Funktion
an, sodass die zugehörige Funktion  umkehrbar ist. Zeichne für diesen Wert von
umkehrbar ist. Zeichne für diesen Wert von  den Graphen der Umkehrfunktion von
den Graphen der Umkehrfunktion von  in Abbildung 4 ein und berücksichtige dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
in Abbildung 4 ein und berücksichtige dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
Es gilt
Abbildung 4 zeigt den Graphen der Funktion

Abb. 4
(3 BE)
b)
Gib den Term einer in  definierten und umkehrbaren Funktion
definierten und umkehrbaren Funktion  an, die folgende Bedingung erfüllt: Der Graph von
an, die folgende Bedingung erfüllt: Der Graph von  und der Graph der Umkehrfunktion von
und der Graph der Umkehrfunktion von  haben keinen gemeinsamen Punkt.
haben keinen gemeinsamen Punkt.
(2 BE)
(20 BE)
1
1. Schritt: Ableitungen bilden
Mit Hilfe der Produktregel und der Kettenregel folgt:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
An der Stelle  besitzt der Graph von
besitzt der Graph von  somit einen Tiefpunkt.
4. Schritt: Lage bestimmen
somit einen Tiefpunkt.
4. Schritt: Lage bestimmen
 Bei dem Extrempunkt des Graphen von
Bei dem Extrempunkt des Graphen von  handelt es sich um einen Tiefpunkt mit den Koordinaten
handelt es sich um einen Tiefpunkt mit den Koordinaten 
2
a)
b)
Aus der folgenden Hilfsabbildung wird deutlich, dass die betrachtete Fläche in drei Teilstücke aufgeteilt werden kann, wobei die beiden grün eingefärbten Flächen wegen der Symmetrie des Graphen von  zur
zur  -Achse gleichgroß sind:
-Achse gleichgroß sind:
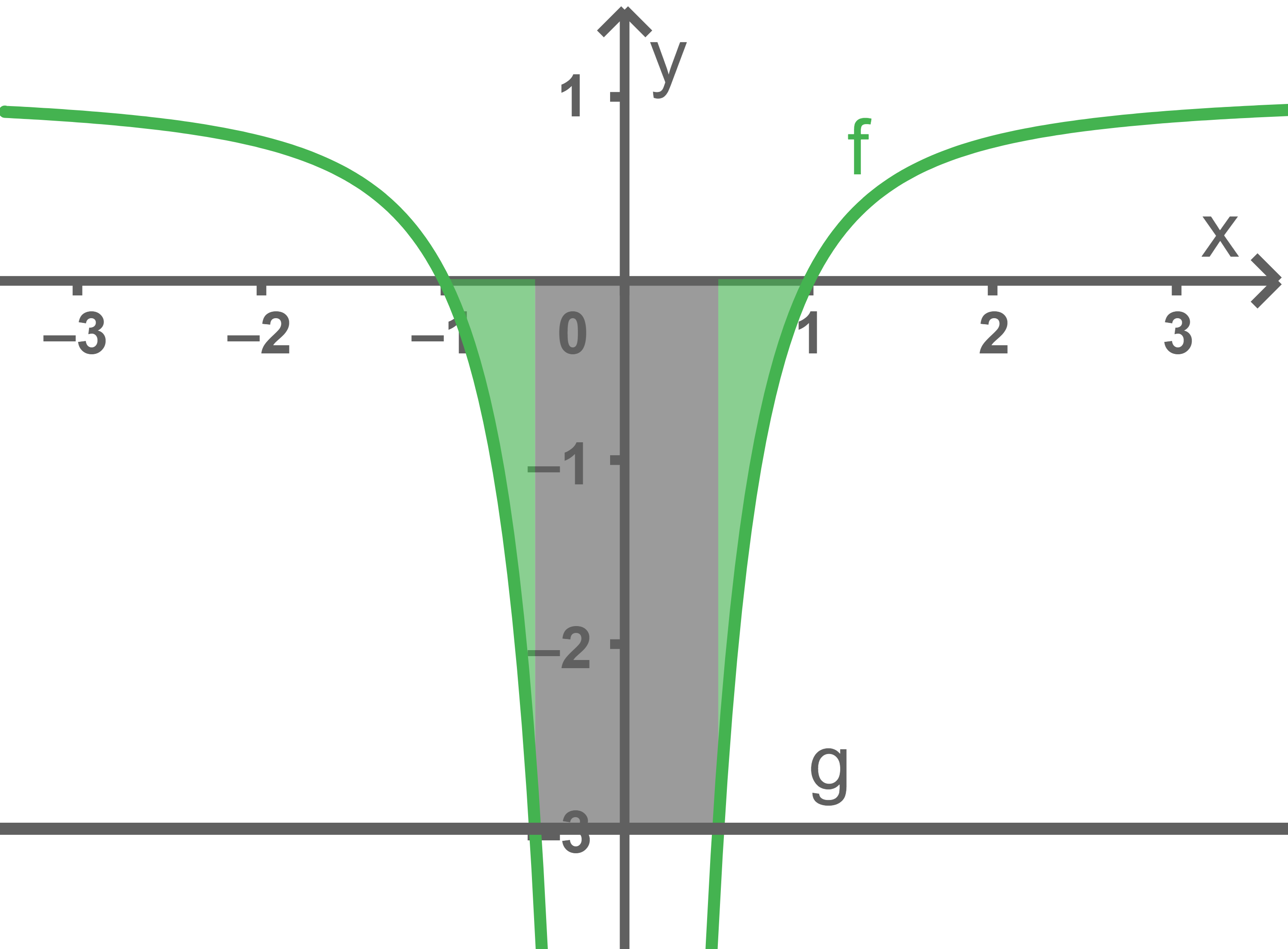 Mit Hilfe der bekannten Nullstellen des Graphen von
Mit Hilfe der bekannten Nullstellen des Graphen von  und den Schnittstellen mit dem Graphen von
und den Schnittstellen mit dem Graphen von  folgt für den Inhalt der rechten grünen Fläche:
folgt für den Inhalt der rechten grünen Fläche:
![\( \begin{array}[t]{rll}
A_1 &=& \left|\displaystyle\int_{0,5}^{1}f(x)\;\mathrm dx \right| \\[5pt]
&=& \left|\displaystyle\int_{0,5}^{1}\left(1-\dfrac{1}{x^2} \right)\;\mathrm dx \right| \\[5pt]
&=& \left| \left[x+\dfrac{1}{x} \right]_{0,5}^1 \right| \\[5pt]
&=& \left\vert1+\dfrac{1}{1} - \left(0,5+\dfrac{1}{0,5} \right)\right\vert\\[5pt]
&=& \vert-0,5\vert\\[5pt]
&=& 0,5\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/6ee1319dcdee6bfa7c94a28e4c7421d45e052b44c49d573d147e1b8497da0f45_light.svg) Der Flächeninhalt der grauen Fläche, eines Rechtecks mit den Seitenlängen
Der Flächeninhalt der grauen Fläche, eines Rechtecks mit den Seitenlängen  und
und  ist gegeben durch
ist gegeben durch ![\(A_2 = 1\cdot 3 = 3\;[\text{FE}].\)](https://www.schullv.de/resources/formulas/494d0e3f01ef22d51f8899e31614353c283298a83b6efd91e5eb3db362ed9e61_light.svg) Für den gesamten Flächeninhalt folgt somit:
Für den gesamten Flächeninhalt folgt somit:


![\( = 2\cdot 0,5 + 3 = 4\;[\text{FE}]\)](https://www.schullv.de/resources/formulas/133632b9a2bbd5c5838ba681ccd36577112f604ae4c445fcd96953f443a45454_light.svg)

3
a)
- Graph
schneidet die
-Achse an den Stellen
und
Der Graph von
muss an diesen Stellen also die Steigung
haben, was zutrifft, da der Graph von
dort Extremstellen besitzt.
Der Graphschneidet die
-Achse ca. im Punkt
An der Stelle
muss der Graph von
somit die Steigung
besitzen. Anlegen einer Tangente an den Graphen von
an der Stelle
lässt auf eine Steigung von ungefähr
schließen.
- Graph
schneidet die
-Achse an den Stellen
und
An diesen Stellen müsste der Graph von
also die Steigung
haben. Da das nicht der Fall ist, kommt Graph
nicht infrage.
- Graph
besitzt zwar die gleichen Schnittpunkte mit der
-Achse wie Graph
schneidet die
-Achse aber im Punkt
Der Graph von
müsste daher an der Stelle
die Steigung
besitzen. Oben würde aber bereits nachgewiesen, dass die Steigung an dieser Stelle ca.
beträgt. Graph
kann daher ebenfalls nicht zur gesuchten Ableitungsfunktion von
gehören.
b)
Da der Graph von
4
a)
Größtmöglichen Wert angeben
Damit eine Funktion umkehrbar ist, darf sie jeden Funktionswert nur einmal annehmen.Der Graph der Cosinusfunktion besitzt an der Stelle  seinen ersten Tiefpunkt und nimmt somit danach einen Funktionswert an, den er vorher bereits hatte.
seinen ersten Tiefpunkt und nimmt somit danach einen Funktionswert an, den er vorher bereits hatte.
Somit ist der größtmögliche Wert von
der größtmögliche Wert von  für den die Funktion
für den die Funktion  umkehrbar ist.
Graph der Umkehrfunktion einzeichnen
umkehrbar ist.
Graph der Umkehrfunktion einzeichnen
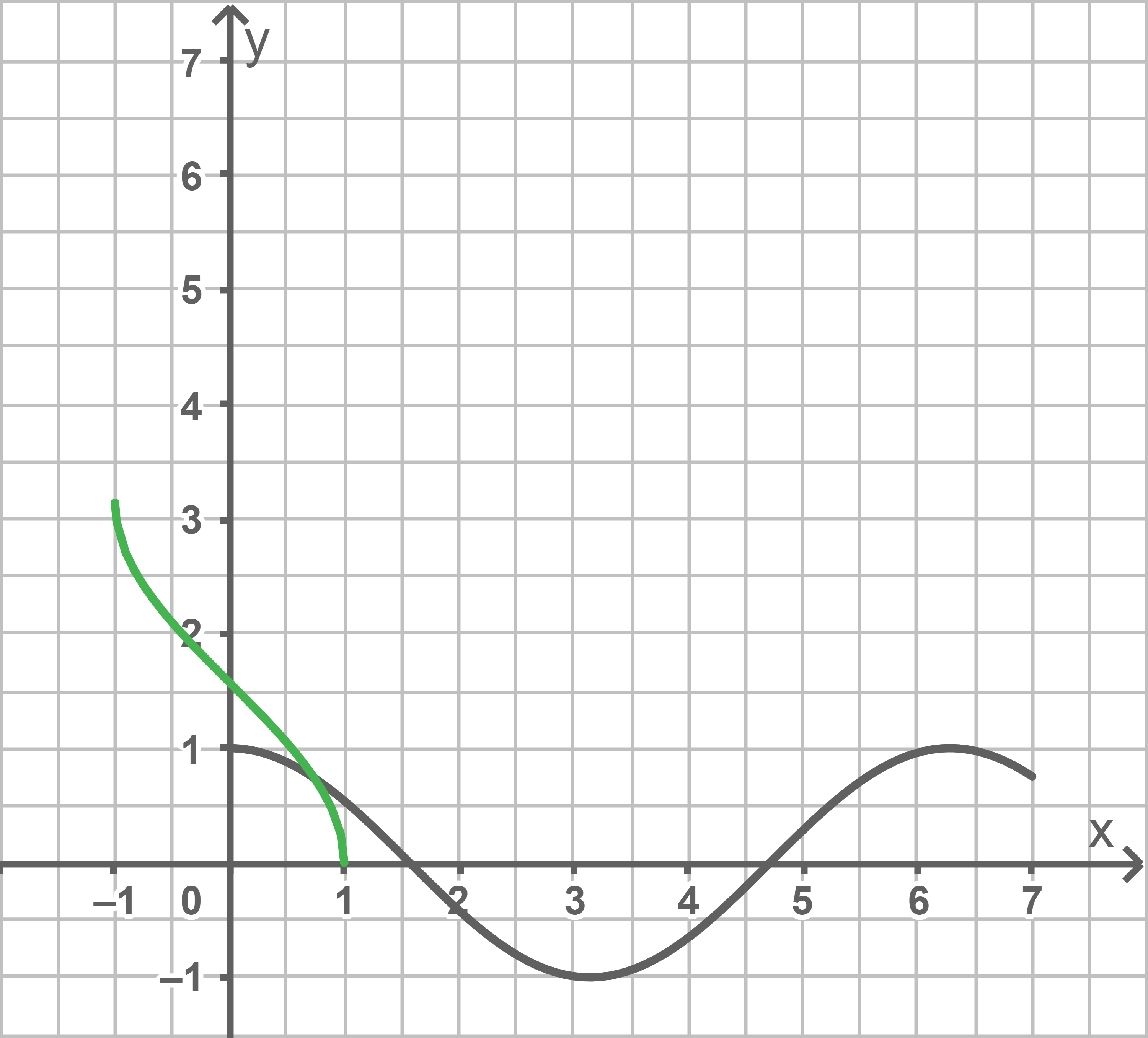
Somit ist

b)
Ein mögliches Beispiel ist die Funktion  Diese ist auf
Diese ist auf  definiert und umkehrbar. Der Graph der zugehörigen Umkehrfunktion, dem natürlichen Logarithmus, hat zudem keinen gemeinsamen Punkt mit dem Graph von
definiert und umkehrbar. Der Graph der zugehörigen Umkehrfunktion, dem natürlichen Logarithmus, hat zudem keinen gemeinsamen Punkt mit dem Graph von 