Geometrie Prüfungsteil B

Aufgabengruppe 1

In einem kartesischen Koordinatensystem sind die Ebene $E:x_1+x_3=2$ , der Punkt $A\left(0\mid\sqrt{2}\mid2\right)$ und die Gerade $g:\vec{X}=\vec{A}+\lambda\cdot\begin{pmatrix}-1\\\sqrt{2}\\1\end{pmatrix}$ , $\lambda\in\mathbb{R}$ , gegeben.

a)

Beschreibe, welche besondere Lage die Ebene $E$ im Koordinatensystem hat. Weise nach, dass die Ebene $E$ die Gerade $g$ enthält. Gib die Koordinaten der Schnittpunkte von $E$ mit der $x_1$ -Achse und mit der $x_3$ -Achse an und veranschauliche die Lage der Ebene $E$ sowie den Verlauf der Geraden $g$ in einem kartesischen Koordinatensystem (vgl. Abbildung).

(6P)

b)

Berechne im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt.

(3P)

c)

Das Lot von $M$ auf $g$ schneidet $g$ im Punkt $B$ . Im Modell stellt $B$ den Punkt der Achterbahn dar, in dem der gerade Abschnitt endet und die Kurve beginnt. Bestimme die Koordinaten von $B$ und berechne den Kurvenradius im Modell.
(Teilergebnis: $B\left(-1\mid2\sqrt{2}\mid3\right))$

(5P)

d)

Das Ende der Rechtskurve wird im Koordinatensystem durch den Punkt $C$ beschrieben. Begründe, dass für den Ortsvektor des Punkts $C$ gilt: $\vec{C}=\vec{M}+\vec{v}$ .

(2P)

e)

Ein Wagen der Achterbahn durchfährt den Abschnitt, der im Modell durch die Strecke $[AB]$ und den Viertelkreis von $B$ nach $C$ dargestellt wird, mit einer durchschnittlichen Geschwindigkeit von $15\frac{\text{m}}{\text{s}}$ . Berechne die Zeit, die der Wagen dafür benötigt, auf Zehntelsekunden genau, wenn eine Längeneinheit im Koordinatensystem $10\,\text{m}$ in der Realität entspricht.

(4P)

(20P)

Aufgabengruppe 2

Abbildung 1 zeigt eine Sonnenuhr mit einer gegenüber der Horizontalen geneigten, rechteckigen Grundplatte, auf der sich ein kreisförmiges Zifferblatt befindet...

Aufgabengruppe 1

a) $\blacktriangleright$ Besondere Lage der Gerade im Koordinatensystem

Die Ebene $E$ hat folgende Gleichung

$E: \quad x_1 +x_3 = 2$

Du sollst die besondere Lage dieser Ebene im Koordinatensystem beschreiben.

Der Normalenvektor der Ebene hat die Koordinate $x_2=0$ , das bedeutet, dass der Normalenvektor senkrecht auf der $x_2$ -Achse steht. Das absolute Glied der Ebenengleichung ist nicht null. Somit ist die Ebene parallel zur $x_2$ -Achse.

$\blacktriangleright$ Zeige, dass die Ebene die Gerade enthält

In der Aufgabenstellung ist außerdem der Punkt $A(0 \mid \sqrt{2} \mid 2)$ und die Gerade $g$ gegeben

$g: \quad \vec{x}=\vec{A}+\lambda \begin{pmatrix}-1\\ \sqrt{2}\\1\end{pmatrix}$ $=\begin{pmatrix}0\\ \sqrt{2}\\2\end{pmatrix} +\lambda \begin{pmatrix}-1\\ \sqrt{2}\\1\end{pmatrix}$

Du sollst nun zeigen, dass die Gerade $g$ in $E$ liegt. Bestimme dafür zunächst die allgemeinen Koordinaten der Punkte auf $g$ und setze diese dann in die Ebenengleichung ein.

Die Punkte auf der Gerade $g$ haben folgende Form $P(-\lambda \mid \sqrt{2}+ \sqrt{2}\lambda \mid 2+ \lambda)$ .

Setze die Koordinaten in die Gleichung von $E$ ein. Damit die Gerade in der Ebene liegt, müssen all ihre Punkte in der Ebene liegen.

$\begin{array}[t]{rll} -\lambda + 2+ \lambda&=&2 \\[5pt] 2&=&2 \quad \checkmark \end{array}$

Somit liegen alle Punkte der Gerade in der Ebene. Die Ebene enthält die Gerade $g$ .

$\blacktriangleright$ Schnittpunkte mit den Koordinatenachsen

Deine Aufgabe ist es, den Schnittpunkt der Ebene $E$ mit der $x_1$ - und der $x_3$ -Achse zu berechnen.

1. Schritt: $\boldsymbol{x_1}$ -Achse

Für den Schnittpunkt mit der $x_1$ -Achse gilt $x_2 = x_3 = 0$ . Setze diese Koordinaten in die Ebenengleichung ein und löse nach $x_1$ auf.

$\begin{array}[t]{rll} x_1&=&2 \end{array}$

Der Schnittpunkt mit der $x_1$ -Achse lautet dann $S_1(2 \mid 0 \mid 0)$ .

2. Schritt: $\boldsymbol{x_3}$ -Achse

Für den Schnittpunkt mit der $x_3$ -Achse gilt $x_1 = x_2 = 0$ . Setze diese Koordinaten in die Ebenengleichung ein und löse nach $x_3$ auf.

$\begin{array}[t]{rll} x_3&=&2 \end{array}$

Der Schnittpunkt mit der $x_3$ -Achse lautet dann $S_1(0 \mid 0 \mid 2)$ .

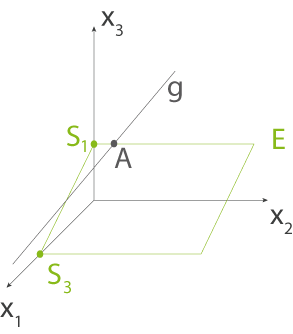
$\blacktriangleright$ Ebene und Gerade zeichnen

Du sollst nun noch die Ebene und die Gerade in ein kartesisches Koordinatensystem einzeichnen. Zeichne zunächst die Schnittpunkte mit den Koordinatenachsen und den Punkt $A$ ein. Dann kannst du die Ebene und die Gerade mithilfe der Punkte einzeichnen. Hier wird noch einmal deutlich, dass die Ebene parallel zur $x_2$ -Achse verläuft.

Grafik eines dreidimensionalen Koordinatensystems mit Ebenen und Punkten.

b) $\blacktriangleright$ Winkel berechnen

In diesen Aufgabenteil ist die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt, gesucht. Den Winkel $\alpha$ zwischen einer Ebene mit Normalenvektor $\vec{n}$ und einem Vektor $\vec{v}$ berechnest du mit folgender Formel

$\sin \alpha = \dfrac{\vec{n} \cdot \vec{v}}{\left| \vec{n}\right| \cdot \left| \vec{v}\right| }$

Für die Ebene, die die Horizontale beschreibt, gilt $x_3 = 0$ . Ein möglicher Normalenvektor lautet somit

$\vec{n} = \begin{pmatrix}0 \\0 \\1\end{pmatrix}$

Der Vektor, der die Richtung der Achterbahn beschreibt, lautet

$\vec{v} = \begin{pmatrix}-1 \\ \sqrt{2} \\1\end{pmatrix}$

Setze die Vektoren in die Formel ein und berechne den Winkel.

$\begin{array}[t]{rll} \sin \alpha &=&\dfrac{\vec{n} \cdot \vec{v}}{\left| \vec{n}\right| \cdot \left| \vec{v}\right| } \\[5pt] \sin \alpha &=&\dfrac{\begin{pmatrix}0 \\0 \\1\end{pmatrix} \cdot \begin{pmatrix}-1 \\ \sqrt{2} \\1\end{pmatrix}}{\left| \begin{pmatrix}0 \\0 \\1\end{pmatrix}\right| \cdot \left|\begin{pmatrix}-1 \\ \sqrt{2} \\1\end{pmatrix}\right| } \\[5pt] \sin \alpha &=&\dfrac{0\cdot (-1) + 0 \cdot \sqrt{2} + 1 \cdot 1}{1 \cdot \sqrt{(-1)^2 + \sqrt{2}^2 + 1^2}} \\[5pt] \sin \alpha &=&\dfrac{1}{\sqrt{4}} \\[5pt] \sin \alpha &=&\dfrac{1}{2} \quad \scriptsize \mid\; \sin^{-1}()\\[5pt] \alpha&=&30° \\[5pt] \end{array}$

Die Achterbahn steigt in einem Winkel von 30° an.

c) $\blacktriangleright$ Lotfußpunkt von $\boldsymbol{M}$ auf $\boldsymbol{g}$ bestimmen

Das Lot von $M$ auf $g$ schneidet die Gerade im Punkt $B$ , du sollst die Koordinaten dieses Punktes bestimmen.

Dafür kannst du in zwei Schritten vorgehen:

Stelle eine Hilfsebene $H$ auf, die senkrecht auf der Gerade $g$ steht und durch den Punkt $M$ verläuft.

Berechne den Schnittpunkt der Ebene $H$ und der Gerade $g$ , das ist gerade der Lotfußpunkt $B$ .

1. Schritt: Hilfsebene aufstellen

Die allgemeine Koordinatengleichung einer Ebene lautet:

$E: \quad ax_1 + bx_2 + cx_3 = d$

Da die Hilfsebene $H$ senkrecht auf $g$ stehen soll, sind die Koordinaten des Richtungsvektors von $g$ die Koeffizienten der Koordinatengleichung von $H$ :

$H: \quad -x_1 + \sqrt{2}x_2 + x_3 = d$

Die Ebene $H$ soll den Punkt $M$ enthalten. Um $d$ zu bestimmen, setzt du die Koordinaten von $M(0 \mid 3\sqrt{2} \mid 2)$ in $H$ ein.

$\begin{array}[t]{rll} d&=&-0 + \sqrt{2}\cdot 3 \sqrt{2} + 2 \\[5pt] d&=&6 + 2 = 8 \end{array}$

Die Gleichung der Hilfsebene lautet dann

$H: \quad -x_1 + \sqrt{2}x_2 + x_3 = 8$

2. Schritt: Lotfußpunkt berechnen

Um den Lotfußpunkt $B$ zu bestimmen, berechnest du den Schnittpunkt von $H$ und $g$ .

Nutze dafür die allgemeine Form der Punkte auf $g$ und setze diese in die Gleichung von $H$ ein und löse nach $\lambda$ auf.

Die Punkte auf der Gerade $g$ haben folgende Form $P(-\lambda \mid \sqrt{2}+ \sqrt{2}\lambda \mid 2+ \lambda)$ .

$\begin{array}[t]{rll} -(-\lambda) + \sqrt{2}(\sqrt{2}+ \sqrt{2}\lambda) +2 + \lambda&=&8 \\[5pt] \lambda + 2 + 2 \lambda + 2+ \lambda&=&8\quad \scriptsize \mid\; -4 \\[5pt] 4 \lambda &=& 4\quad \scriptsize \mid\; :4\\[5pt] \lambda &=& 1 \end{array}$

Setze nun $\lambda = 1$ in die Geradengleichung von $g$ ein, um die Koordinaten von $B$ zu berechnen.

$\begin{pmatrix}0\\ \sqrt{2}\\2\end{pmatrix} +1\cdot \begin{pmatrix}-1\\ \sqrt{2}\\1\end{pmatrix} = \begin{pmatrix}-1\\ 2\sqrt{2}\\ 3\end{pmatrix}$

Die Koordinaten des Punkt $B$ lauten $B(-1 \mid 2\sqrt{2} \mid 3)$ .

$\blacktriangleright$ Kurvenradius berechnen

Als nächstes sollst du den Kurvenradius berechnen. Der gesuchte Radius entspricht gerade dem Abstand des Mittelpunkts $M$ vom Lotfußpunkt $B$ . Diesen berechnest du mit dem Betrag des Vektors $\overrightarrow{MB}$ .

$\begin{array}[t]{rll} \left|\overrightarrow {MB}\right|&=&\left|\overrightarrow {OB}- \overrightarrow {OM}\right| \\[5pt] &=&\left|\begin{pmatrix}-1\\ 2\sqrt{2}\\ 3\end{pmatrix} - \begin{pmatrix}0\\ 3\sqrt{2}\\ 2\end{pmatrix}\right|\\[5pt] &=&\left|\begin{pmatrix}-1\\ -\sqrt{2}\\ 1\end{pmatrix}\right|\\[5pt] &=&\sqrt{(-1)^2 + (-\sqrt{2})^2 + 1^2}\\[5pt] &=&\sqrt{1 + 2 +1}\\[5pt] &=& \sqrt{4}\ =\ 2 \end{array}$

Der Kurvenradius beträgt 2.

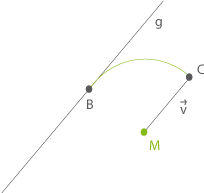
d) $\blacktriangleright$ Begründe die Entstehung des Ortsvektors von $\boldsymbol{C}$

Das Ende der Rechtskurve ist im Koordinatensystem der Punkt $C$ . Du sollst begründen warum für den Ortsvektor $\vec{C} = \vec{M}+ \vec{v}$ gilt.

Mache dir dafür am besten eine Skizze.

Geometrische Darstellung mit Punkten B, C und M sowie einer gekrümmten Linie und einer Geraden g.

Die Verbindungsstrecke $[MB]$ steht senkrecht auf der Gerade $g$ und vom Punkt $B$ geht ein viertel Kreis ab und endet im Punkt $C$ . Ein viertel Kreis hat einen Innenwinkel von 90°, das bedeutet, dass die Strecke $[MC]$ parallel zur Gerade $g$ verläuft, um von $M$ zu $C$ zu gelangen musst du also in Richtung $\vec{v}$ gehen. Der Abstand zwischen $C$ und $M$ ist der Radius vom Kreis mit Radius $M$ , diesen hast du bereits berechnet $r=2$ .

Außerdem gilt: $\left|\vec{v}\right| = \sqrt{(-1)^2 + \sqrt{2}^2 + 1^2} = 2$ .

Das entspricht gerade dem Radius. Somit gilt für den Ortsvektor von $C$ :

$\vec{C} = \vec{M} + 1 \cdot \vec{v}$ .

e) $\blacktriangleright$ Zeit, die der Wagen benötigt, berechnen

Auf der Achterbahn fährt ein Wagen mit 15 m/s die Strecke von $A$ nach $B$ und den Kreisbogen nach $C$ . Du sollst die Zeit berechnen, die der Wagen für die Strecke benötigt.

Berechne zunächst die Länge der Strecke $[AB]$ und anschließend die Länge des Kreisbogens mit der Formel für den Umfang von einem Kreis ( $U= 2 \cdot \pi \cdot r$ ).

$\overrightarrow{AB}= \overrightarrow{OB}-\overrightarrow{OA} = \begin{pmatrix}-1\\ 2\sqrt{2}\\ 3\end{pmatrix}-\begin{pmatrix}0\\ \sqrt{2}\\ 2\end{pmatrix}\ =\begin{pmatrix}-1\\ \sqrt{2}\\ 1\end{pmatrix}$

$\left|\overrightarrow{AB}\right| = \left|\begin{pmatrix}-1\\ \sqrt{2}\\ 1\end{pmatrix}\right| = \sqrt{(-1)^2 + \sqrt{2}^2 + 1^2} = 2$

Der Kreisbogen ist ein Viertel des Kreises, somit berechnet sich seine Länge durch $\frac{1}{4} \cdot U$ .

$L_{\text{Kreisbogen}} = \frac{1}{4} \cdot 2 \cdot \pi \cdot 2 = \pi$

Für die gesamte Strecke, die der Wagen zurücklegt, erhältst du somit

$2 + \pi = 5,14159$ .

Da im Koordinatensystem 1 Einheit 10 m entspricht, sind das 51,4159 m.

Die benötigte Zeit $t$ für eine Strecke $s$ mit Geschwindigkeit $v$ berechnest du mit folgender Formel:

$t = \dfrac{s}{v}$

Somit erhältst du

$t = \dfrac{51,4159 \text{ m}}{15 \frac{\text{m}}{\text{s}}} = 3,43 \text{ s}$

Der Wagen benötigt für die Strecke 3,43 Sekunden.

Aufgabengruppe 2

a) $\blacktriangleright$ Bestimme die Koordinaten von $\boldsymbol{C}$

Die rechteckige Grundplatte $ABCD$ einer Sonnenuhr hat die Punkte $A(5 \mid -4 \mid 0)$ , $A(5 \mid 4 \mid 0)$ und den Mittelpunkt $M(2,5 \mid 0 \mid 2)$ . Du sollst die Koordinaten des Punkt $C$ bestimmen.

Um den Ortsvektor von $C$ zu bestimmen, kannst du die Vektorsumme vom Ortsvektor von $A$ und zwei mal die Strecke von $A$ nach $M$ verwenden. Da $M$ der Mittelpunkt der Strecke $[AC]$ ist, gilt $\overrightarrow{AC} = 2 \cdot \overrightarrow{AM}$ .

$\overrightarrow{OC} = \overrightarrow{OA} + 2 \cdot \overrightarrow{AM}$ $=\begin{pmatrix}5\\-4 \\0\end{pmatrix} + 2 \cdot \begin{pmatrix}2,5 - 5 \\ 0 -(-4) \\ 2-0\end{pmatrix}$ $=\begin{pmatrix}5\\-4 \\0\end{pmatrix} + \begin{pmatrix} - 5 \\ 8 \\4\end{pmatrix}$ $= \begin{pmatrix}0\\4\\4\end{pmatrix}$

Die Koordinaten von Punkt $C$ lauten $C(0 \mid 4 \mid 4)$ .

$\blacktriangleright$ Ebenengleichung in Normalenform aufstellen

Die quadratische Grundplatte der Sonnenuhr liegt in der Ebene $E$ . Du sollst die Gleichung dieser Ebene in Koordinatenform aufstellen. Gehe dafür folgendermaßen vor:

Stelle die Parametergleichung der Ebene auf.

Wandle die Parametergleichung der Ebene in die Koordinatenform um.

Bestimme einen Normalenvektor der Ebene.

Stelle die Normalengleichung der Ebene auf.

1. Schritt: Parametergleichung aufstellen

Stelle eine Parametergleichung der Ebene $E$ mithilfe der Punkte $A$ , $B$ und $C$ auf. Dabei ist $A$ der Aufpunkt und $\overrightarrow{AB}$ und $\overrightarrow{AC}$ die Richtungsvektoren.

$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix}5\\4\\0\end{pmatrix} - \begin{pmatrix}5\\-4\\0\end{pmatrix} = \begin{pmatrix}0\\8\\0\end{pmatrix}$

$\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = \begin{pmatrix}0\\4\\4\end{pmatrix} - \begin{pmatrix}5\\-4\\0\end{pmatrix} = \begin{pmatrix}-5\\8\\4\end{pmatrix}$

$\begin{array}[t]{rll} E: \quad \vec{x}&=&\overrightarrow{OA} + r \cdot \overrightarrow{AB} + s \cdot \overrightarrow{AC} \\[5pt] &=&\begin{pmatrix}5\\-4\\0\end{pmatrix} + r \begin{pmatrix}0\\8\\0\end{pmatrix} + s \cdot \begin{pmatrix}-5\\8\\4\end{pmatrix} \end{array}$

2. Schritt: Koordinatengleichung aufstellen

Die gerade bestimmte Parameterform wandelst du jetzt in die Koordinatenform um, indem du dir die Gleichungen für $x_1$ , $x_2$ und $x_3$ aufschreibst, dann mit zwei der Gleichungen $r$ und $s$ bestimmst und diese in die dritte Gleichung einsetzt.

Aus der 3. Gleichung folgt $s = \frac{1}{4}x_3$ . Setze dieses Ergebnis in die erste Gleichung ein.

$\begin{array}[t]{rll} x_1&=&5 - 5 \cdot \frac{1}{4}x_3\quad \scriptsize \mid\;\cdot 4 \\[5pt] 4x_1 &=&20 - 5 x_3\quad \scriptsize \mid\;+5x_3 \\[5pt] 4x_1 + 5 x_3 &=&20 \end{array}$

Die Koordinatengleichung der Ebene lautet somit $E: \quad 4x_1 + 5 x_3 =20$ .

3. Schritt: Normalenvektor bestimmen

Einen Normalenvektor der Ebene $E$ kannst du aus der Koordinatengleichung ablesen:

$\vec{n} = \begin{pmatrix}4 \\0 \\5\end{pmatrix}$

4. Schritt: Normalengleichung aufstellen

Um die Normalengleichung der Ebene aufstellen zu können, benötigst du einen Aufpunkt, du kannst beispielsweise $A$ verwenden, und den gerade bestimmten Normalenvektor.

Die Normalengleichung lautet dann $\left[\vec{x} - \vec{A}\right] \cdot \vec{n} = 0$ :

$\left[\vec{x} - \begin{pmatrix}5\\-4\\0\end{pmatrix}\right] \cdot \begin{pmatrix}4\\0\\5\end{pmatrix} = 0$

b) $\blacktriangleright$ Winkel berechnen

In diesen Aufgabenteil ist gefragt, für welchen Breitengrad $\varphi$ die Sonnenuhr gebaut wurde. Dabei gilt für den Neigungswinkel $\alpha$ gegenüber der Horizontalen und den Breitengrad:

$\alpha + \varphi = 90°$

Bestimme also den Neigungswinkel um dann den Breitengrad berechnen zu können.

Den Winkel $\alpha$ zwischen zwei Ebenen mit Normalenvektoren $\vec{n_1}$ und $\vec{n_2}$ berechnest du mit folgender Formel

$\cos \alpha = \dfrac{\vec{n_1} \cdot \vec{n_2}}{\left| \vec{n_1}\right| \cdot \left| \vec{n_2}\right| }$

Für die Ebene, die die Horizontale beschreibt, gilt $x_3 = 0$ . Ein möglicher Normalenvektor lautet somit

$\vec{n_1} = \begin{pmatrix}0 \\0 \\1\end{pmatrix}$

Den Normalenvektor der Ebene $E$ hast du bereits in Aufagbenteil a) berechnet:

$\vec{n_2} = \begin{pmatrix}4 \\ 0 \\5\end{pmatrix}$

Setze die Vektoren in die Formel ein und berechne den Winkel.

$\begin{array}[t]{rll} \cos \alpha &=&\dfrac{\vec{n_1} \cdot \vec{n_2}}{\left| \vec{n_1}\right| \cdot \left| \vec{n_2}\right| } \\[5pt] \cos \alpha &=&\dfrac{\begin{pmatrix}0 \\0 \\1\end{pmatrix} \cdot \begin{pmatrix}4 \\ 0 \\5\end{pmatrix}}{\left| \begin{pmatrix}0 \\0 \\1\end{pmatrix}\right| \cdot \left|\begin{pmatrix}4 \\ 0 \\5\end{pmatrix}\right| } \\[5pt] \cos \alpha &=&\dfrac{0\cdot 4 + 0 \cdot 0 + 1 \cdot 5}{1 \cdot \sqrt{4^2 + 0^2 + 5^2}} \\[5pt] \cos \alpha &=&\dfrac{5}{\sqrt{41}} \quad \scriptsize \mid\; \cos^{-1}()\\[5pt] \alpha &=&38,66° \end{array}$

Der Neigungswinkel hat 38,66°. Für den Breitengrad gilt somit:

$\varphi = 90° - 38,66° = 51,34°$

Die Sonnenuhr wurde für den 51. Breitengrad gebaut.

c) $\blacktriangleright$ Zeige, dass Polstab senkrecht auf der Grundplatte steht.

Der Polstab wird durch die Strecke $[MS]$ beschrieben, mit $S(4,5 \mid 0 \mid 4,5)$ . Du sollst zeigen, dass der Polstab senkrecht auf der Grundplatte steht. Dafür musst du zeigen, dass das Skalarprodukt zwischen dem Vektor $\overrightarrow{MS}$ und einem Vektor in der Ebene, beispielsweise $\overrightarrow{AM}$ gleich null ist.

Stelle die Vektoren auf und berechne das Skalarprodukt.

$\overrightarrow{MS} = \overrightarrow{OS} - \overrightarrow{OM}$ $= \begin{pmatrix}4,5 \\ 0\\4,5\end{pmatrix} - \begin{pmatrix}2,5 \\0\\2\end{pmatrix}$ $= \begin{pmatrix}2 \\ 0 \\2,5\end{pmatrix}$

$\overrightarrow{AM} = \overrightarrow{OM} - \overrightarrow{OS}$ $= \begin{pmatrix}2,5 \\0\\2\end{pmatrix} - \begin{pmatrix}5 \\ -4\\0\end{pmatrix}$ $=\begin{pmatrix}-2,5 \\ 4 \\2\end{pmatrix}$

$\overrightarrow{AM} \cdot \overrightarrow{MS} = \begin{pmatrix}-2,5 \\ 4 \\2\end{pmatrix} \cdot \begin{pmatrix}2 \\ 0 \\2,5\end{pmatrix}$ $= (-2,5) \cdot 2 + 0 \cdot 0 + 2 \cdot 2,5 = 0$

Das Skalarprodukt ist null, somit steht der Polstab senkrecht auf der Grundplatte.

$\blacktriangleright$ Länge des Polstabs berechnen berechnen

Du sollst nun die Länge des Polstabs berechnen. Diese kannst du mithilfe des Betrags des Vektors $\overrightarrow{MS}$ berechnen.

$\left|\overrightarrow{MS}\right| = \left| \begin{pmatrix}2 \\ 0 \\2,5\end{pmatrix}\right|$ $= \sqrt{2^2 + 0^2 + 2,5^2} = 3,202$

Da eine Einheit im Koordinatensystem 10 cm entspricht, hat der Polstab eine Länge von 32 cm.

d) $\blacktriangleright$ Zeige, dass der Schatten des Polstabs außerhalb der Grundplatte liegt

Das Sonnenlicht, das zu einem bestimmten Zeitpunkt auf die Sonnenuhr fällt, wird durch $\vec{u} = \begin{pmatrix}6\\6\\-13\end{pmatrix}$ beschrieben. Du sollst zeigen, dass der Schatten des Polstabs außerhalb der Grundplatte liegt. Dafür stellst du die Gerade durch die Spitze des Polstabs mit Richtungsvektor $\vec{u}$ auf und berechnest den Schnittpunkt mit der Ebene $E$ .

1. Schritt: Geradengleichung aufstellen

Als Aufpunkt für die Gerade kannst du den Punkt $S$ nehmen, der Richtungsvektor ist $\vec{u}$ , somit lautet die Geradengleichung:

$\vec{x} = \begin{pmatrix}4,5\\ 0 \\4,5\end{pmatrix} + t \begin{pmatrix}6 \\6 \\-13\end{pmatrix}$

2. Schritt: Schnittpunkt berechnen

Die Punkte auf der Gerade haben folgende Form

$P(4,5+6t \mid 6t \mid 4,5-13t)$

Setze die Koordinaten in die Koordinatengleichung der Ebene $E$ ein und berechne $t$ .

$\begin{array}[t]{rll} 4 \cdot (4,5+6t) + 5 \cdot (4,5-13t)&=&20\\[5pt] 18 + 24 t + 22,5 -65t&=&20 \\[5pt] -41t+40,5&=&20\quad \scriptsize \mid\;-40,5 \\[5pt] -41t &=& -20,5\quad \scriptsize \mid\;:(-41) \\[5pt] t &=& 0,5 \end{array}$

Setze nun $t=0,5$ in die Geradengleichung ein um den Schnittpunkt zu erhalten:

$\begin{pmatrix}4,5\\ 0 \\4,5\end{pmatrix} + 0,5 \begin{pmatrix}6 \\6 \\-13\end{pmatrix} = \begin{pmatrix}7,5 \\ 3 \\ -2\end{pmatrix}$

Der Schattenpunkt der Spitze lautet $\overline{S}(7,5 \mid 3 \mid -2)$ . Du sollst nun noch begründen, warum dieser Punkt außerhalb der Grundfläche liegt. Damit der Schatten der Spitze innerhalb der Grundfläche liegt, muss der Abstand zum Mittelpunkt kleiner sein, als die Strecke vom Mittelpunkt zu einem der Eckpunkte.

Die Strecke $[AM]$ hat folgende Länge:

$\left|\overrightarrow{AM}\right| = \left|\begin{pmatrix}-2,5 \\ 4 \\2\end{pmatrix}\right|$ $= \sqrt{(-2,5)^2+ 4^2 +2^2} = \sqrt{26,25}$

Die Strecke vom Schattenpunkt zum Mittelpunkt hat folgende Länge:

$\left|\overrightarrow{\overline{S}M}\right| = \left|\begin{pmatrix}2,5-7,5 \\ 0-3 \\ 2-(-2) \end{pmatrix}\right|$ $= \sqrt{(-5)^2+ (-3)^2 +4^2} = \sqrt{50}$

Der Abstand des Schattenpunkts zum Mittelpunkt ist somit größer. Das hat zur Folge, dass der Schatten der Spitze außerhalb der Grundfläche liegt.

e) $\blacktriangleright$ Begründe, warum Zeitpunkt in d) vor 12 Uhr

Du sollst begründen, warum der Zeitpunkt $t_0$ vor 12 Uhr liegt.

Betrachtest du die Punkte $A$ und $B$ , so fällt auf, dass $A$ eine negative $x_2$ -Koordinate und $B$ eine positive $x_2$ -Koordinate hat. Betrachtest du den Punkt $\overline{S}$ , so stellst du fest, dass dieser eine positive $x_2$ -Koordinate hat. Der Zeitpunkt 12 Uhr liegt in der Mitte der Strecke $[AB]$ , somit hat er eine $x_2$ -Koordinate von null. Damit folgt, dass $t_0$ vor 12 Uhr liegt.