Teil B
1
Gegeben ist die in  definierte Funktion
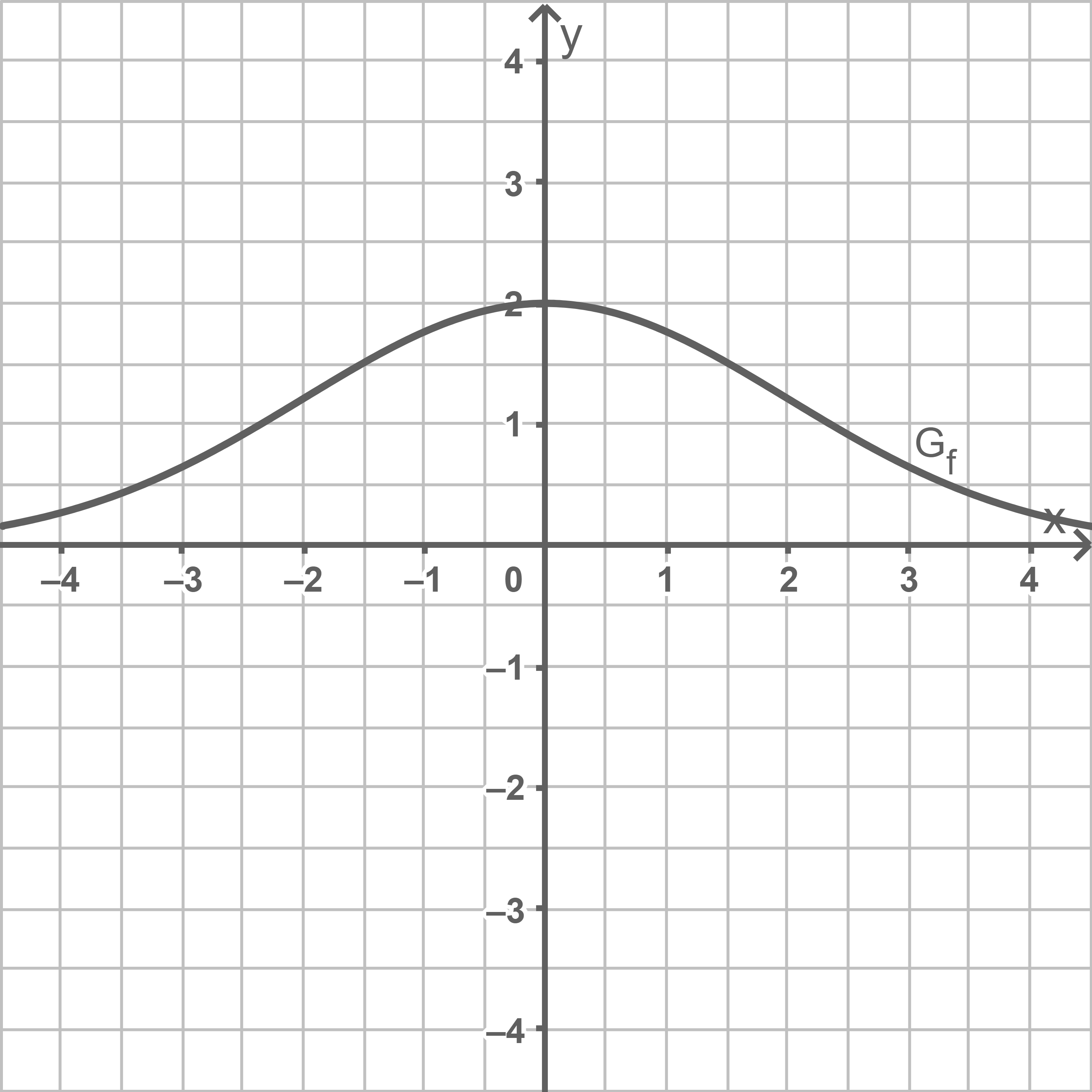
definierte Funktion  Abbildung 1 zeigt den Graphen
Abbildung 1 zeigt den Graphen  von
von  der die
der die  -Achse als waagrechte Asymptote besitzt.
-Achse als waagrechte Asymptote besitzt.
 das Rechteck mit den Eckpunkten
das Rechteck mit den Eckpunkten  und
und 
 die in
die in ![\(]- \infty ; 0]\)](https://www.schullv.de/resources/formulas/6b4658a57022c7cb32e9987e8d8e42c1ae9031f26391ab1d772a0ee9d3c0d994_light.svg) definierten Funktionen
definierten Funktionen  Somit gilt
Somit gilt  wobei sich
wobei sich  und
und  im Definitionsbereich unterscheiden.
im Definitionsbereich unterscheiden.

Abb. 1
a)
Berechne die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse und weise rechnerisch nach, dass
-Achse und weise rechnerisch nach, dass  symmetrisch bezüglich der
symmetrisch bezüglich der  -Achse ist.
-Achse ist.
(2 BE)
b)
Der Punkt  ist einer der beiden Wendepunkte von
ist einer der beiden Wendepunkte von  Die Tangente an
Die Tangente an  im Punkt
im Punkt  wird mit
wird mit  bezeichnet. Ermittle eine Gleichung von
bezeichnet. Ermittle eine Gleichung von  und berechne die Stelle, an der
und berechne die Stelle, an der  die
die  -Achse schneidet.
-Achse schneidet.
Betrachtet wird für jeden Wert
(zur Kontrolle:  )
)
(5 BE)
c)
Zeichne für  das Rechteck
das Rechteck  in Abbildung 1 ein.
in Abbildung 1 ein.
(1 BE)
d)
Berechne denjenigen Wert von  für den
für den  gilt.
gilt.
(3 BE)
e)
Gib in Abhängigkeit von  die Seitenlängen des Rechtecks
die Seitenlängen des Rechtecks  an und begründe, dass der Flächeninhalt des Rechtecks durch den Term
an und begründe, dass der Flächeninhalt des Rechtecks durch den Term  gegeben ist.
gegeben ist.
(3 BE)
f)
Es gibt einen Wert von  für den der Flächeninhalt
für den der Flächeninhalt  des Rechtecks
des Rechtecks  maximal ist. Berechne diesen Wert von
maximal ist. Berechne diesen Wert von 
Betrachtet werden für
(4 BE)
g)
Begründe mithilfe der ersten Ableitung von  dass
dass  für jeden Wert von
für jeden Wert von  umkehrbar ist. Skizziere in Abbildung 1 den Graphen der Umkehrfunktion von
umkehrbar ist. Skizziere in Abbildung 1 den Graphen der Umkehrfunktion von 
(4 BE)
h)
Gib alle Werte von  an, für die der Graph von
an, für die der Graph von  und der Graph der Umkehrfunktion von
und der Graph der Umkehrfunktion von  keinen gemeinsamen Punkt haben.
keinen gemeinsamen Punkt haben.
(2 BE)
2
Abbildung 2 zeigt ein Haus mit einer Dachgaube, deren Vorderseite schematisch in Abbildung 3 dargestellt ist. Die Vorderseite wird modellhaft durch das Flächenstück beschrieben, das der Graph  der Funktion
der Funktion  aus Aufgabe 1, die
aus Aufgabe 1, die  -Achse und die Geraden mit den Gleichungen
-Achse und die Geraden mit den Gleichungen  und
und  einschließen. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
einschließen. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.

Abb. 2
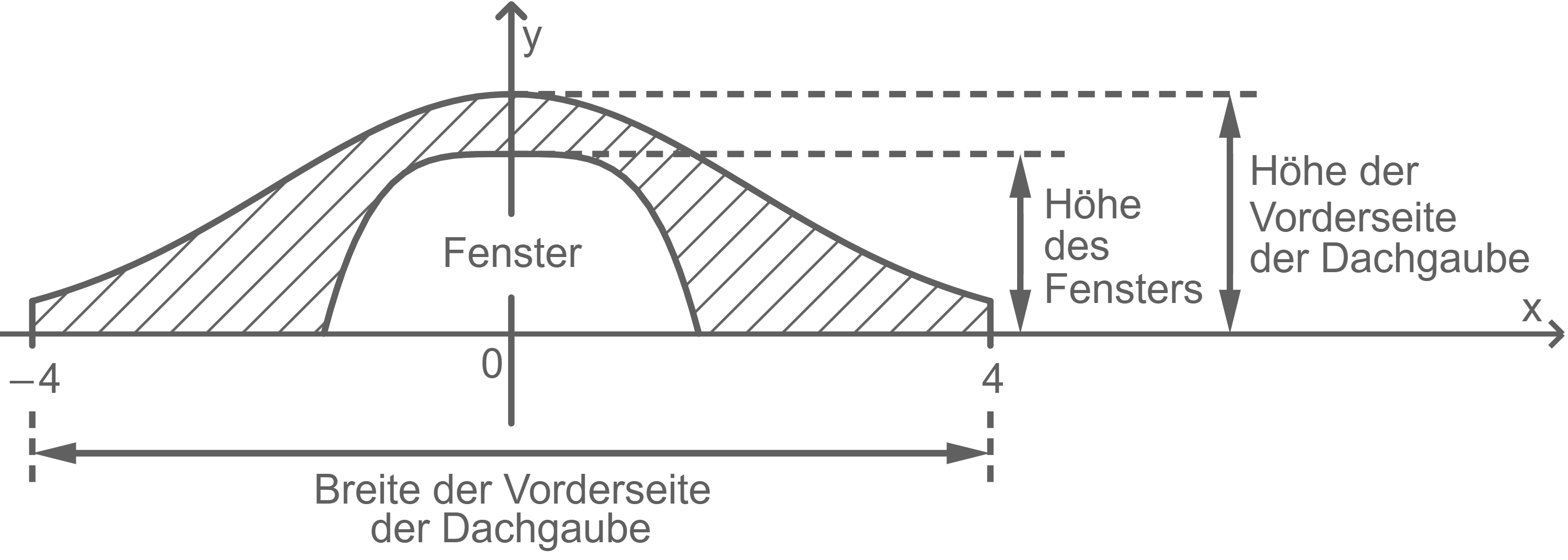
Abb. 3
a)
Gib die Breite und die Höhe der Vorderseite der Dachgaube an.
In der Vorderseite der Dachgaube befindet sich ein Fenster. Dem Fenster entspricht im Modell das Flächenstück, das der Graph der Funktion
(2 BE)
b)
Begründe, dass  negativ und
negativ und  positiv ist.
positiv ist.
Um den Flächeninhalt der Vorderseite der Dachgaube zu ermitteln, wird eine Stammfunktion
(2 BE)
c)
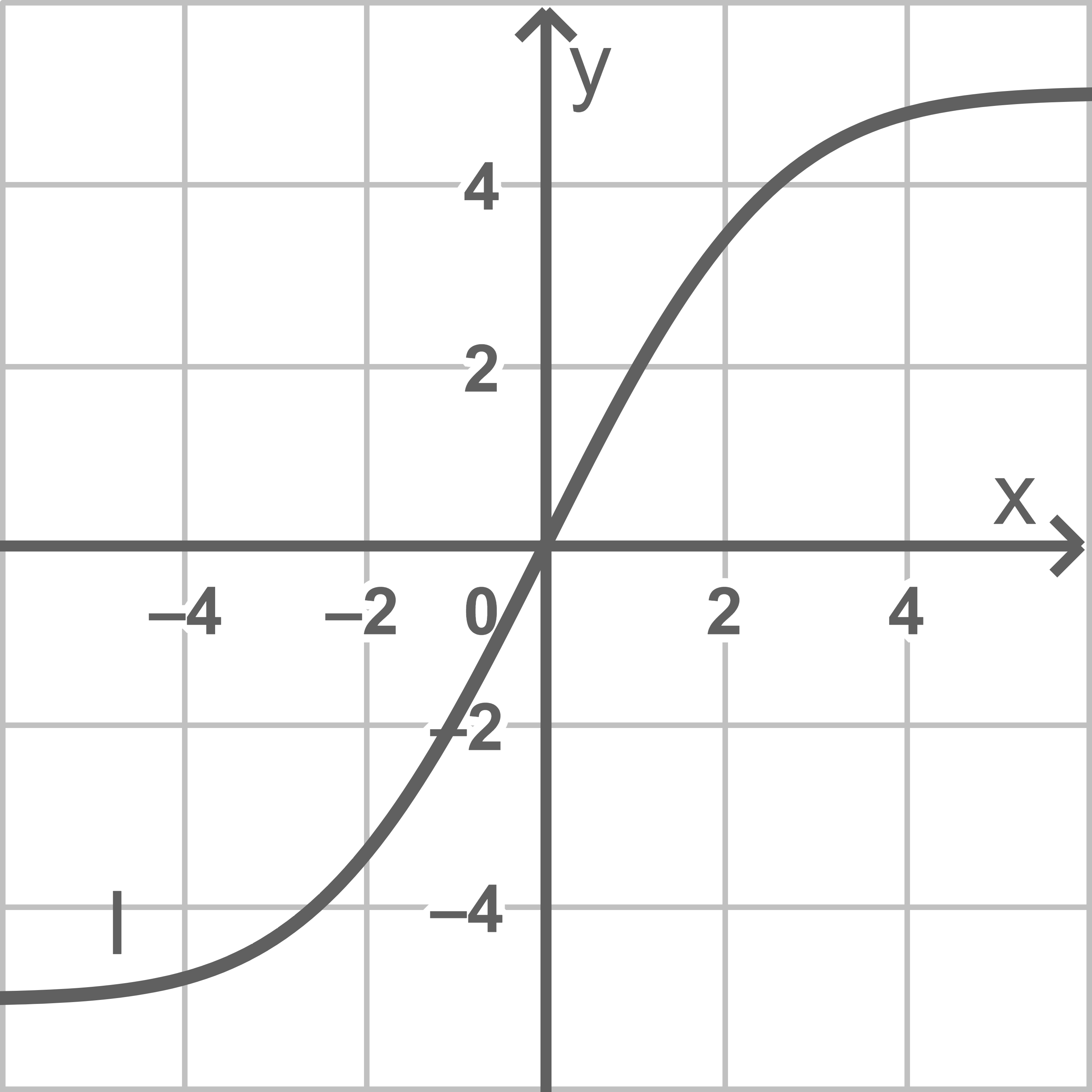
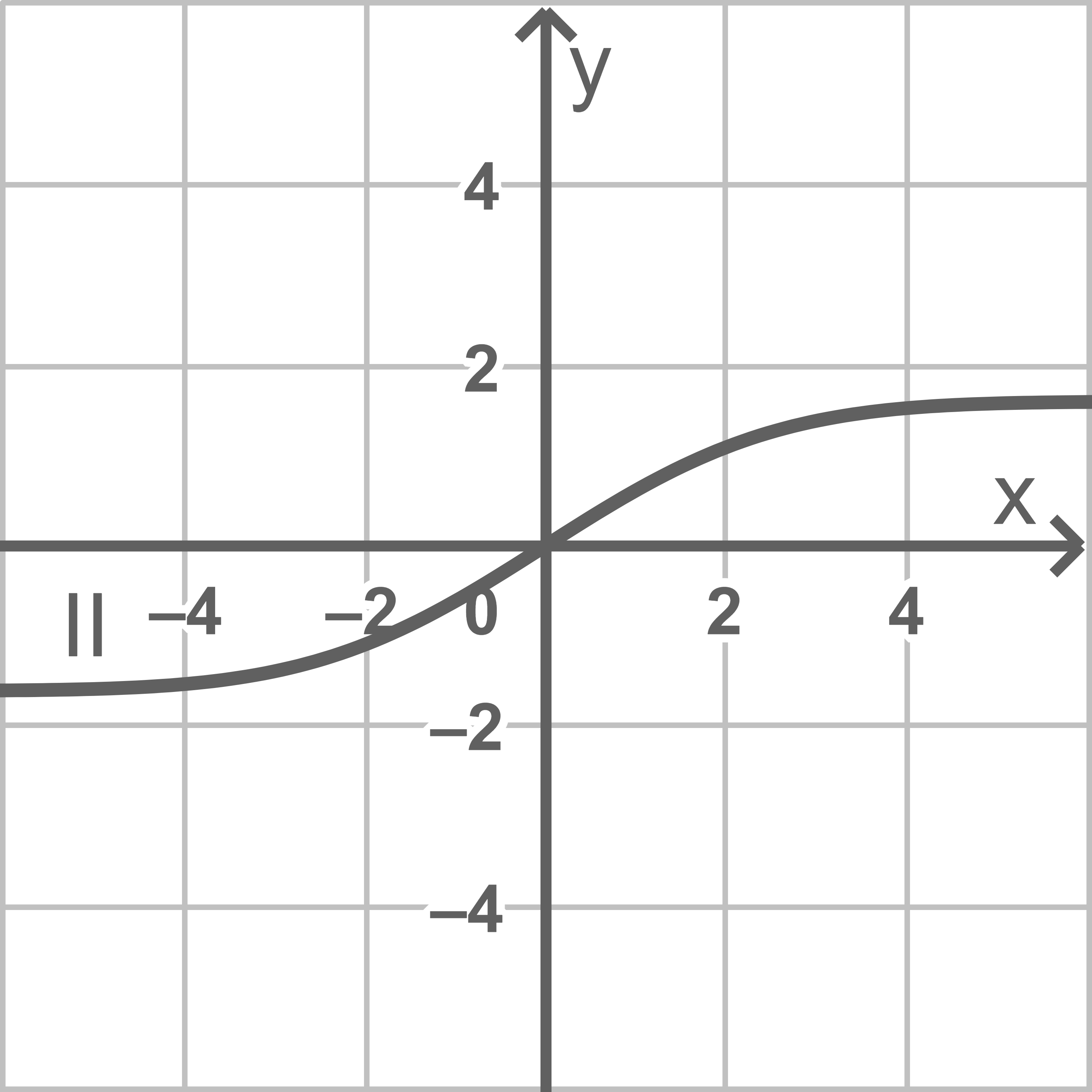
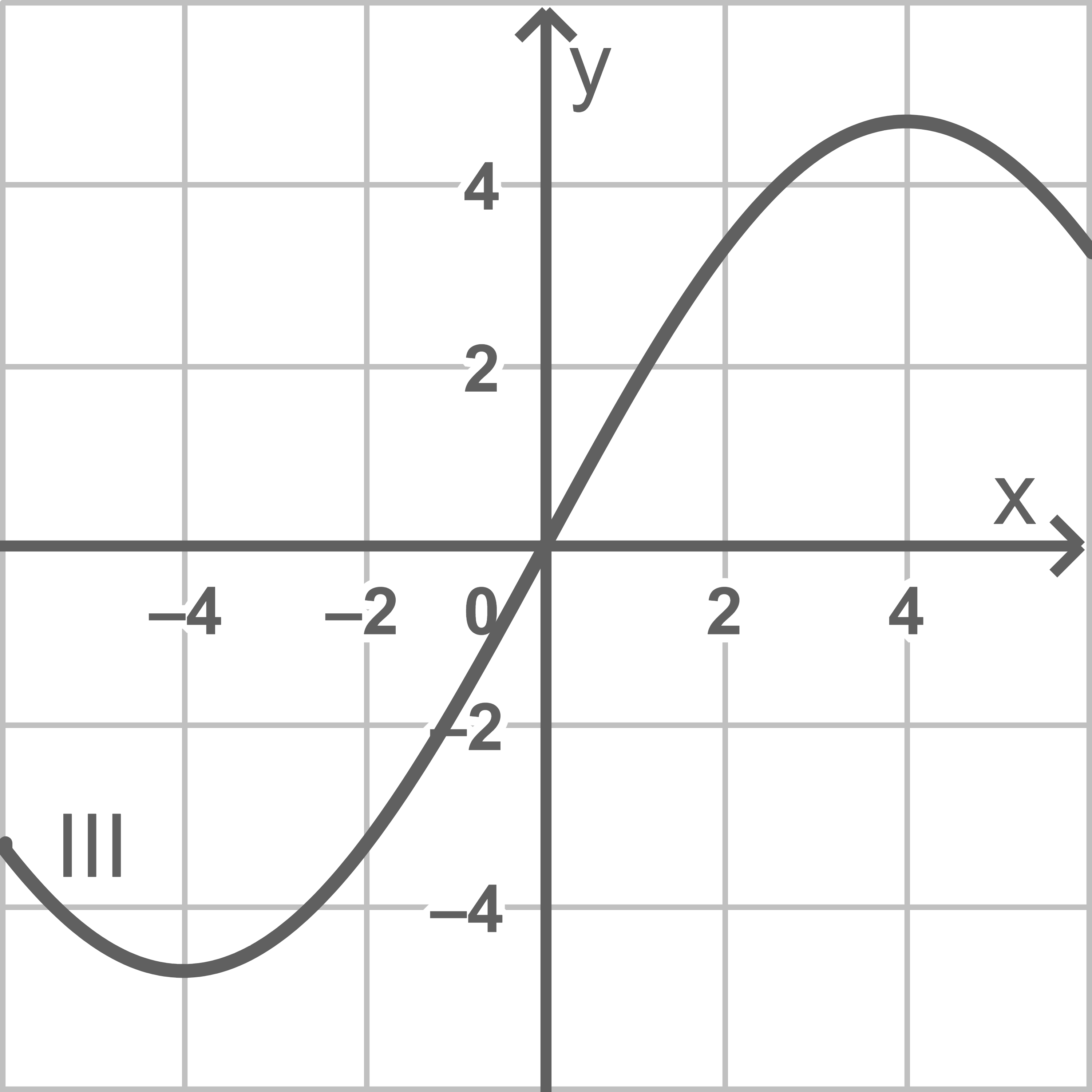
Einer der Graphen  und
und  ist der Graph von
ist der Graph von  Begründe, dass dies Graph
Begründe, dass dies Graph  ist, indem du jeweils einen Grund dafür angibst, dass Graph
ist, indem du jeweils einen Grund dafür angibst, dass Graph  und Graph
und Graph  nicht infrage kommen.
nicht infrage kommen.



(2 BE)
d)
Bestimme nun mithilfe des Graphen von  aus Aufgabe 2c den Flächeninhalt der gesamten Vorderseite der Dachgaube (einschließlich des Fensters).
aus Aufgabe 2c den Flächeninhalt der gesamten Vorderseite der Dachgaube (einschließlich des Fensters).
Beschreibe unter Einbeziehung dieses Flächeninhalts die wesentlichen Schritte eines Lösungswegs, mit dem der Wert von rechnerisch so bestimmt werden könnte, dass bei einer Fensterhöhe von
rechnerisch so bestimmt werden könnte, dass bei einer Fensterhöhe von  der Teil der Vorderseite der Dachgaube, der in Abbildung 3 schraffiert dargestellt ist, den Flächeninhalt
der Teil der Vorderseite der Dachgaube, der in Abbildung 3 schraffiert dargestellt ist, den Flächeninhalt  hat.
hat.
Beschreibe unter Einbeziehung dieses Flächeninhalts die wesentlichen Schritte eines Lösungswegs, mit dem der Wert von
(5 BE)
e)
Um einen Näherungswert für die Länge der oberen Profillinie der Vorderseite der Dachgaube berechnen zu können, wird  im Bereich
im Bereich  durch vier Kreisbögen angenähert, die nahtlos ineinander übergehen und zueinander kongruent sind. Einer dieser Kreisbögen erstreckt sich im Bereich
durch vier Kreisbögen angenähert, die nahtlos ineinander übergehen und zueinander kongruent sind. Einer dieser Kreisbögen erstreckt sich im Bereich  und ist Teil des Kreises mit Mittelpunkt
und ist Teil des Kreises mit Mittelpunkt  und Radius
und Radius  Berechne den Mittelpunktswinkel des zu diesem Kreisbogen gehörenden Kreissektors und ermittle damit den gesuchten Näherungswert.
Berechne den Mittelpunktswinkel des zu diesem Kreisbogen gehörenden Kreissektors und ermittle damit den gesuchten Näherungswert.
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Koordinaten des Schnittpunkts berechnen
![\(\begin{array}[t]{rll}
f(0)&=&2\cdot\mathrm e^{-\frac{1}{8}\cdot0^2} \\[5pt]
&=&2\cdot 1 \\[5pt]
&=&2
\end{array}\)](https://www.schullv.de/resources/formulas/05622ce5149f884380aa2cf8ead6bfccaad34dedc220163277120489bcf84503_light.svg) Die Koordinaten des Schnittpunkts mit der
Die Koordinaten des Schnittpunkts mit der  -Achse sind somit
-Achse sind somit  Symmetrie nachweisen
Symmetrie nachweisen
![\(\begin{array}[t]{rll}
f(-x)&=&2\cdot\mathrm e^{-\frac{1}{8}\cdot(-x)^2} \\[5pt]
&=&2\cdot\mathrm e^{-\frac{1}{8}\cdot x^2} \\[5pt]
&=&f(x)
\end{array}\)](https://www.schullv.de/resources/formulas/3c829ddbc9c5b8f828e4b49fce080ff26126a7002047bd5b39499e500093dffa_light.svg) Somit ist der Graph
Somit ist der Graph  symmetrisch bezüglich der
symmetrisch bezüglich der  -Achse.
-Achse.
b)
Tangentengleichung ermitteln
Für die Tangente  mit
mit  gilt
gilt


 Damit folgt für die Steigung
Damit folgt für die Steigung  der Tangente:
der Tangente:
![\(\begin{array}[t]{rll}
m&=& f](https://www.schullv.de/resources/formulas/e638a8aba2570f3ef320ffcce2209927536801f72374d36ac7e1722e5bc32645_light.svg) Für den
Für den  -Achsenabschnitt
-Achsenabschnitt  der Tangente folgt durch Einsetzen der Koordinaten von
der Tangente folgt durch Einsetzen der Koordinaten von 
![\(\begin{array}[t]{rll}
w(-2)&=& 2 \mathrm e^{-\frac{1}{2}} \\[5pt]
\mathrm e^{-\frac{1}{2}}\cdot(-2)+b&=& 2 \mathrm e^{-\frac{1}{2}} &\quad \scriptsize \mid\;+2 \mathrm e^{-\frac{1}{2}} \\[5pt]
b&=& 4 \mathrm e^{-\frac{1}{2}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e4abc84044c957e4e5d2b43930cd4d4872b3c8386c15c1aa78c8b8b92d0dc0c6_light.svg) Die Tangentengleichung ergibt sich damit als
Die Tangentengleichung ergibt sich damit als 
 Schnittstelle mit der
Schnittstelle mit der  -Achse berechnen
Die Tangente
-Achse berechnen
Die Tangente  schneidet die
schneidet die  -Achse somit an der Stelle
-Achse somit an der Stelle 
c)
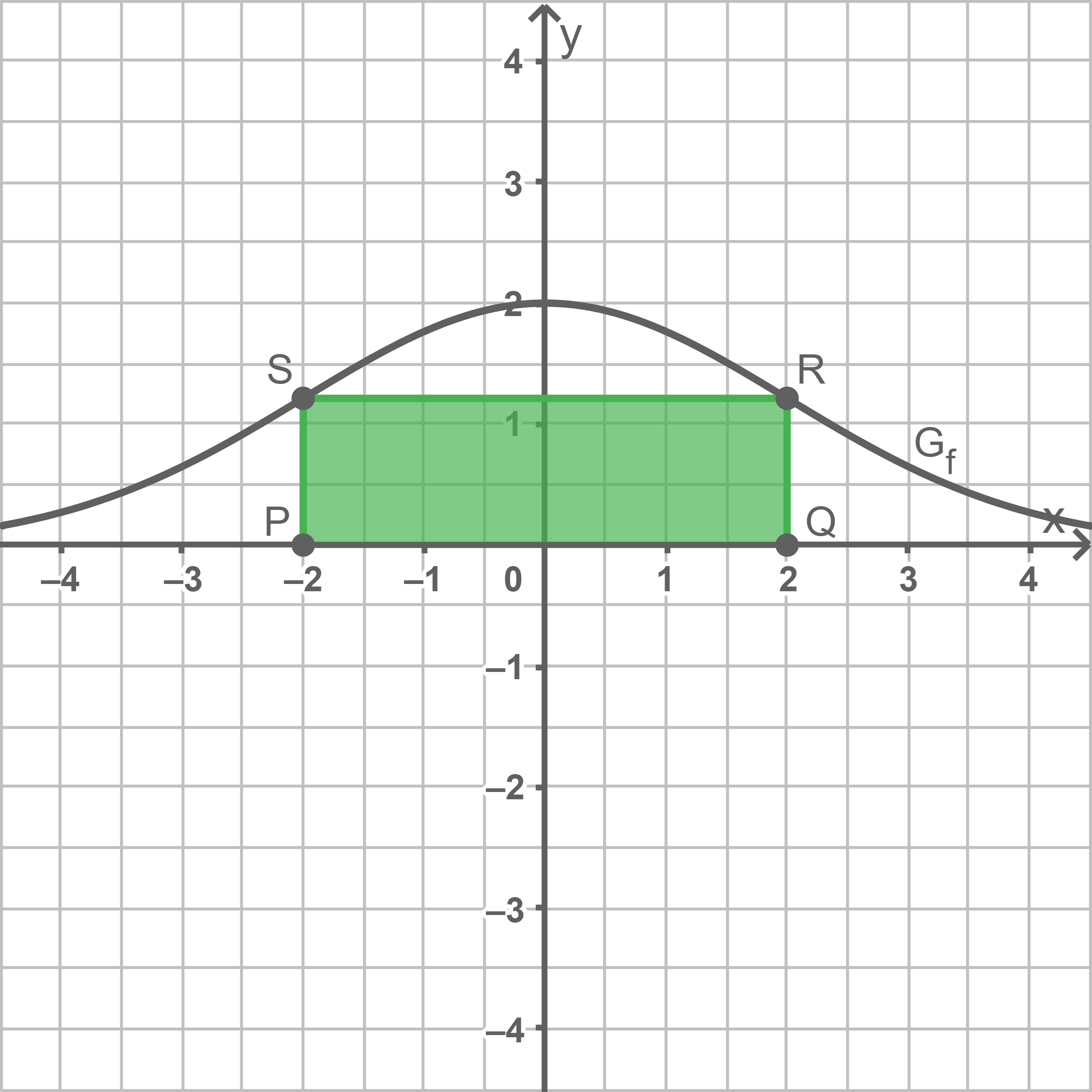
d)
Da  und
und  die gleiche
die gleiche  -Koordinate
-Koordinate  besitzen und
besitzen und  auf der
auf der  -Achse liegt, ist
-Achse liegt, ist  genau dann wenn die
genau dann wenn die  -Koordinate von
-Koordinate von 
 ist, also wenn
ist, also wenn  ist.
ist.
![\(\begin{array}[t]{rll}
f(c) &=& 1 \\[5pt]
2\mathrm e^{-\frac{1}{8}c^2} &=& 1 &\quad \scriptsize \mid\;:2 \\[5pt]
\mathrm e^{-\frac{1}{8}\cdot c^2}&=&\dfrac{1}{2} \\[5pt]
-\dfrac{1}{8}\cdot c^2&=&\ln\left(\dfrac{1}{2}\right)&\quad \scriptsize \mid\;\cdot(-8) \\[5pt]
c^2&=& -8\cdot\ln\left(\dfrac{1}{2}\right)&\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
c&=&\pm \sqrt{-8\cdot\ln\left(\dfrac{1}{2}\right)} \\[5pt]
c&\approx&\pm 2,36
\end{array}\)](https://www.schullv.de/resources/formulas/bfb7948cdb50e4407afbb425762bd41a05dea39c13a39652396a52cd9c9cf9ea_light.svg) Da
Da  folgt
folgt 
e)
Die Länge der beiden vertikalen Rechteckseiten beträgt:
 Die Länge der horizontalen Rechteckseiten ergibt sich durch die Differenz der
Die Länge der horizontalen Rechteckseiten ergibt sich durch die Differenz der  -Koordinaten der Punkte
-Koordinaten der Punkte  und
und  als
als 
 Somit folgt für den Flächeninhalt:
Somit folgt für den Flächeninhalt:



f)
1. Schritt: Ableitungsfunktionen bilden
Mit der Produkt- und Kettenregel folgt:






 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
A](https://www.schullv.de/resources/formulas/581c04f5a4e38cddfa16ffdb0555091ba39315d37a6627f80f97331eebe67928_light.svg) Da stets
Da stets  folgt mit dem Satz des Nullprodukts, dass
folgt mit dem Satz des Nullprodukts, dass  erfüllt sein muss.
erfüllt sein muss.
![\(\begin{array}[t]{rll}
4-c^2&=&0&\quad \scriptsize \mid\;+c^2 \\[5pt]
4&=&c^2&\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
\pm2&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/fd90ad3a93a56412361497c00936f942a9d7bcb9e62082f9df03b84740e0f66c_light.svg) Da
Da  folgt
folgt  3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
A](https://www.schullv.de/resources/formulas/1cb3bba5c7f24dcb49ef45c68984a4e122f9b6de01e135ec50750a07c4d8edf4_light.svg) Die Funktion
Die Funktion  des Flächeninhalts hat somit an der Stelle
des Flächeninhalts hat somit an der Stelle  ein Maximum.
ein Maximum.
g)
Umkehrbarkeit begründen
Da  für beliebiges
für beliebiges  gilt und stets
gilt und stets  folgt, dass
folgt, dass 
 auf dem Intervall
auf dem Intervall ![\(]- \infty ; 0]\)](https://www.schullv.de/resources/formulas/6b4658a57022c7cb32e9987e8d8e42c1ae9031f26391ab1d772a0ee9d3c0d994_light.svg) streng monoton steigend ist. Somit ist
streng monoton steigend ist. Somit ist  für jeden Wert von
für jeden Wert von  umkehrbar.
Graph einzeichnen
umkehrbar.
Graph einzeichnen
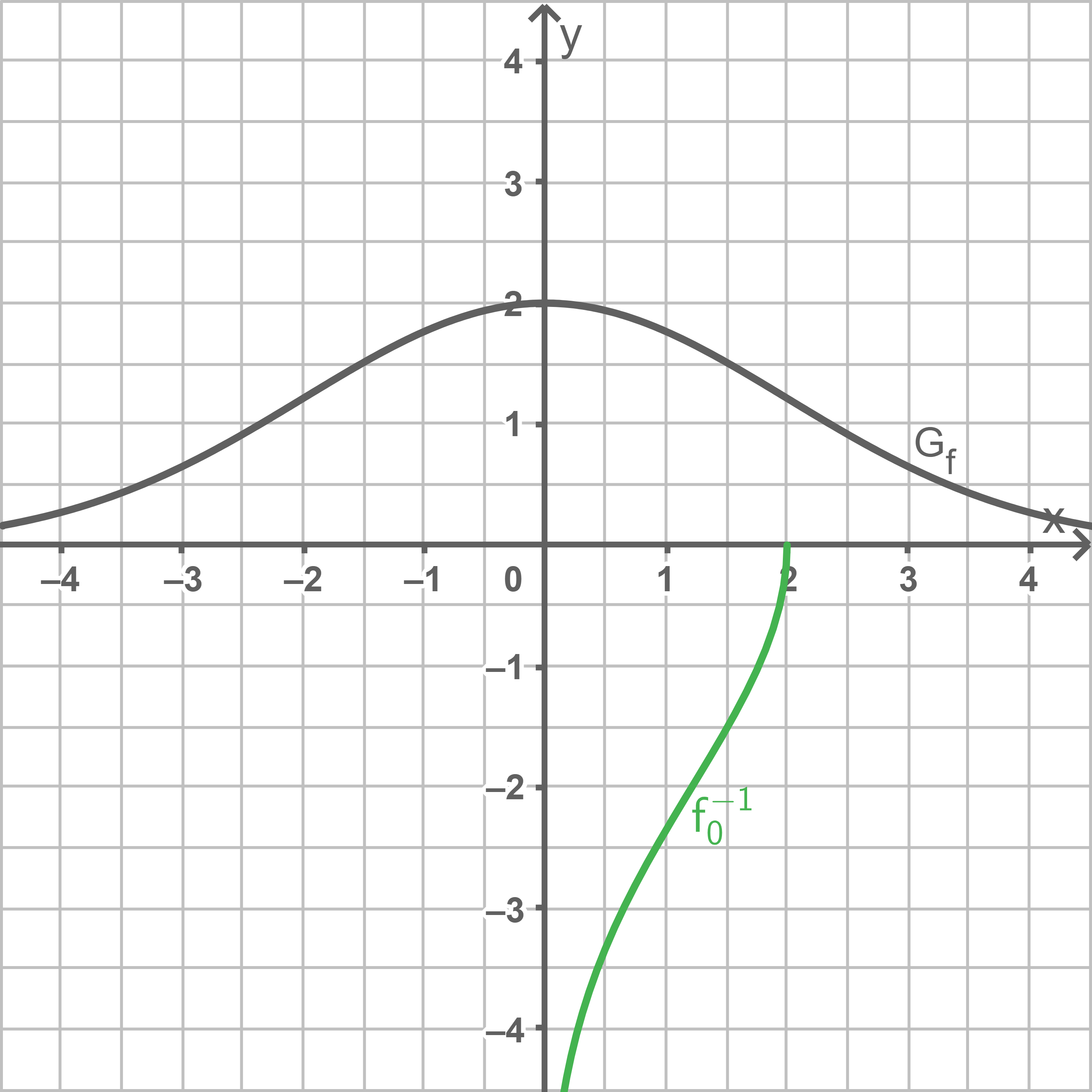

h)
Für positive  verschiebt sich der Graph von
verschiebt sich der Graph von  nach oben, während der Graph von
nach oben, während der Graph von  nach rechts verschoben wird. Da für alle
nach rechts verschoben wird. Da für alle  stets
stets  gilt, besitzen die Graphen von
gilt, besitzen die Graphen von  und
und  für positive
für positive  somit keinen gemeinsamen Punkt.
somit keinen gemeinsamen Punkt.
Wenn negativ und größer als
negativ und größer als  ist, haben die Graphen
ist, haben die Graphen  und
und  ebenfalls keinen gemeinsamen Punkt, da aus der Abbildung aus Aufgabenteil g) deutlich wird, dass bei Verschieben der beiden Graphen nach unten bzw. links erst bei
ebenfalls keinen gemeinsamen Punkt, da aus der Abbildung aus Aufgabenteil g) deutlich wird, dass bei Verschieben der beiden Graphen nach unten bzw. links erst bei  ein Schnittpunkt entsteht.
ein Schnittpunkt entsteht.
Für schneidet der Graph von
schneidet der Graph von  den von
den von  immer, da er weiter nach unten verschoben wird.
immer, da er weiter nach unten verschoben wird.
Wenn
Für
2
a)
Da  folgt für die Breite der Dachgaube
folgt für die Breite der Dachgaube 
 Die Höhe ergibt sich durch den
Die Höhe ergibt sich durch den  -Achsenabschnitt von
-Achsenabschnitt von  als
als 
b)
Bei dem Graphen von  handelt es sich um eine Parabel. Um die Form des Fensters zu erhalten, muss die Parabel nach unten geöffnet sein, was nur dann der Fall ist, wenn
handelt es sich um eine Parabel. Um die Form des Fensters zu erhalten, muss die Parabel nach unten geöffnet sein, was nur dann der Fall ist, wenn  negativ ist.
Zudem muss der Graph von
negativ ist.
Zudem muss der Graph von  dann noch so verschoben werden, dass er einen Bereich oberhalb der
dann noch so verschoben werden, dass er einen Bereich oberhalb der  -Achse einschließt, was durch einen positiven Wert von
-Achse einschließt, was durch einen positiven Wert von  geschieht.
geschieht.
c)
Da  die Steigung seiner Stammfunktion
die Steigung seiner Stammfunktion  beschreibt, muss
beschreibt, muss  an der Stelle
an der Stelle  eine Steigung von
eine Steigung von  haben. Die Steigung der Tangente an den Graphen
haben. Die Steigung der Tangente an den Graphen  an der Stelle
an der Stelle  ist deutlich kleiner als
ist deutlich kleiner als  somit kommt dieser Graph nicht infrage.
somit kommt dieser Graph nicht infrage.
Graph besitzt Extremstellen bei
besitzt Extremstellen bei  und
und  Die Funktion
Die Funktion  hat allerdings keine Nullstellen, wie sich dem Funktionsterm ablesen lässt. Somit kann auch dieser nicht der Graph von
hat allerdings keine Nullstellen, wie sich dem Funktionsterm ablesen lässt. Somit kann auch dieser nicht der Graph von  sein.
sein.
Graph
d)
Flächeninhalt bestimmen
Der gesuchte Flächeninhalt lässt sich über folgendes Integral berechnen:
 Aus der Abbildung des Graphen von
Aus der Abbildung des Graphen von  in Aufgabenteil c) kann ungefähr abgelesen werden:
in Aufgabenteil c) kann ungefähr abgelesen werden:
 und
und  Somit beträgt der Flächeninhalt der gesamten Vorderseite der Dachgaube ungefähr
Somit beträgt der Flächeninhalt der gesamten Vorderseite der Dachgaube ungefähr 
![\( = 9,6\;[\text{m}^2].\)](https://www.schullv.de/resources/formulas/a18a00ace7a512de8de29e133bc05295d72a5b87a701674f3ad33bc846b07c7a_light.svg) Bestimmung von
Bestimmung von  beschreiben
Für eine Fensterhöhe von
beschreiben
Für eine Fensterhöhe von  muss
muss  gelten. Also folgt:
gelten. Also folgt:
 Nullsetzen von
Nullsetzen von  liefert zwei von
liefert zwei von  abhängige Nullstellen
abhängige Nullstellen  und
und 
Folgendes Integral beschreibt dann den Flächeninhalt des Fensters in Abhängigkeit von
 Die Differenz, des zuvor berechneten Flächeninhalts der gesamten Dachgaube mit dem des Fensters beschreibt nun den Flächeninhalt des Teils der Dachgaube, er in der Abbildung schraffiert dargestellt ist in Abhängigkeit von
Die Differenz, des zuvor berechneten Flächeninhalts der gesamten Dachgaube mit dem des Fensters beschreibt nun den Flächeninhalt des Teils der Dachgaube, er in der Abbildung schraffiert dargestellt ist in Abhängigkeit von  Diese wird mit dem gewünschten Wert von
Diese wird mit dem gewünschten Wert von  gleichgestzt und die Gleichung nach
gleichgestzt und die Gleichung nach  aufgelöst.
aufgelöst.
Folgendes Integral beschreibt dann den Flächeninhalt des Fensters in Abhängigkeit von
e)
Mittelpunktswinkel berechnen
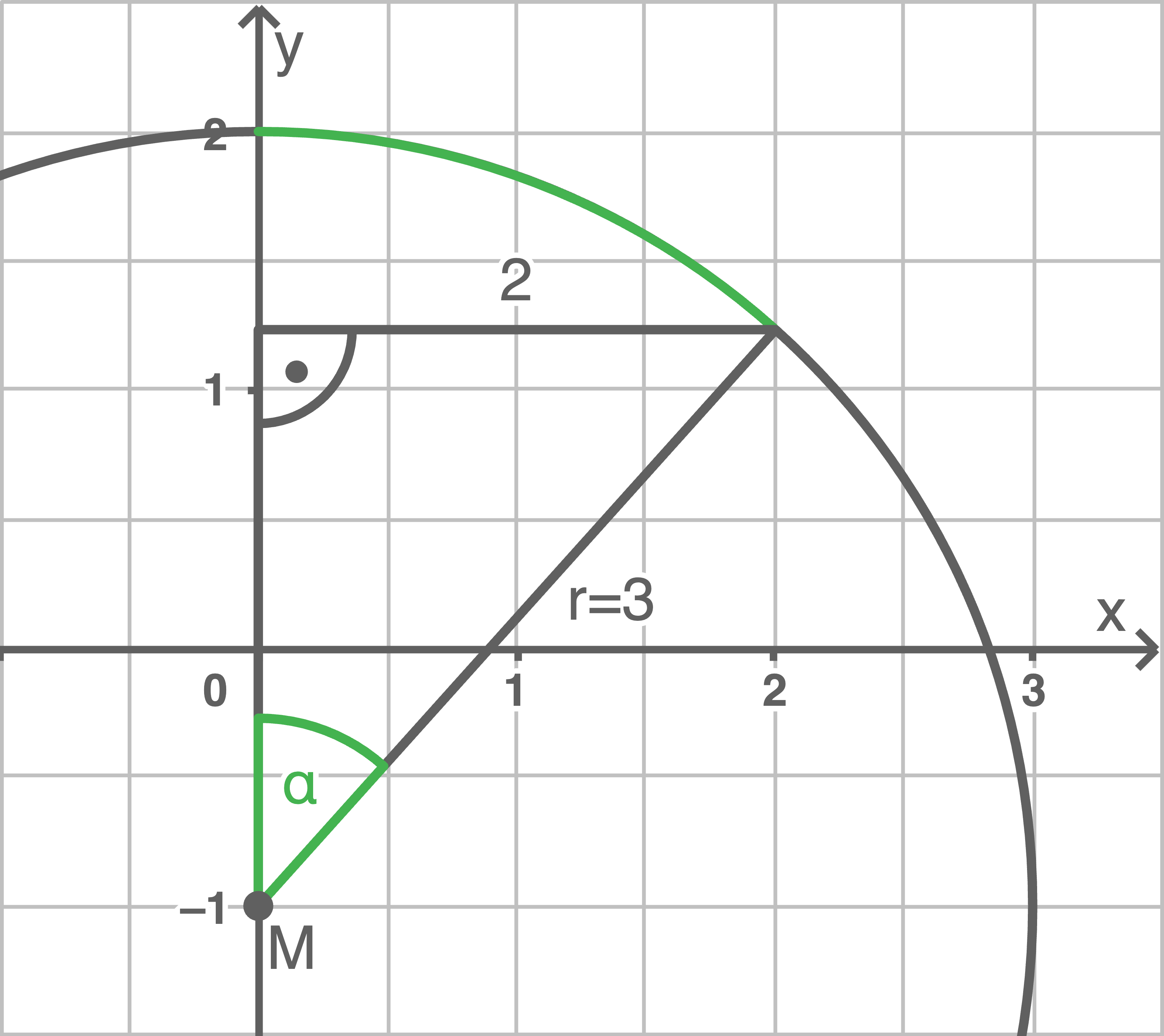 Näherungswert ermitteln
Für die Länge
Näherungswert ermitteln
Für die Länge  des betrachteten Kreisbogens gilt:
des betrachteten Kreisbogens gilt:
![\(\begin{array}[t]{rll}
l_1&=& 2 \pi\cdot r\cdot\dfrac{\alpha}{360^\circ} & \\[5pt]
&=& 2 \pi\cdot 3\cdot\dfrac{41,8^\circ}{360^\circ} & \\[5pt]
&\approx & 2,19 \;[\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/b5189a8e263e069b6dc312e2682989c155fd82f49738fe0662c721dc3047e90e_light.svg) Da die vier Kreisbögen kongruent zueinander sind ergibt sich ein Näherungswert für die gesamte Länge
Da die vier Kreisbögen kongruent zueinander sind ergibt sich ein Näherungswert für die gesamte Länge  der oberen Profillinie der Vorderseite der Dachgaube mit:
der oberen Profillinie der Vorderseite der Dachgaube mit:
![\(\begin{array}[t]{rll}
l&=& 4\cdot l_1 & \\[5pt]
&=& 4\cdot 2,19 \; \text{m} & \\[5pt]
&=& 8,75 \; \text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/833b6407fdce50f15ef70c4c40da6f795b9d2ef47dcc9706a19d47f852c79f96_light.svg)
Da der Kreis den Radius 3 haben soll, besitzt jeder Punkt auf dem Kreisbogen den Abstand 3 zum Mittelpunkt  Der betrachtete Kreisbogen erstreckt sich im Bereich
Der betrachtete Kreisbogen erstreckt sich im Bereich  und somit über eine Strecke von 2 Längeneinheiten entlang der
und somit über eine Strecke von 2 Längeneinheiten entlang der  -Achse.
Durch Skizzieren des Kreissektors sowie der bekannten Werte in ein entsprechendes Koordinatensystem ergibt sich ein rechtwinkliges Dreieck innerhalb des betrachteten Sektors.
Für den Winkel
-Achse.
Durch Skizzieren des Kreissektors sowie der bekannten Werte in ein entsprechendes Koordinatensystem ergibt sich ein rechtwinkliges Dreieck innerhalb des betrachteten Sektors.
Für den Winkel  folgt nun:
folgt nun:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypothenuse}} & \\[5pt]
\sin(\alpha)&=& \dfrac{2}{3} &\quad \scriptsize \mid\; \sin^{-1}\\[5pt]
\alpha&\approx & 41,8^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/2bfbb9b90a51c0974cd47adc096828efa8819818a45f03770b2d1566b948acb2_light.svg)

Hilfsskizze