Teil B
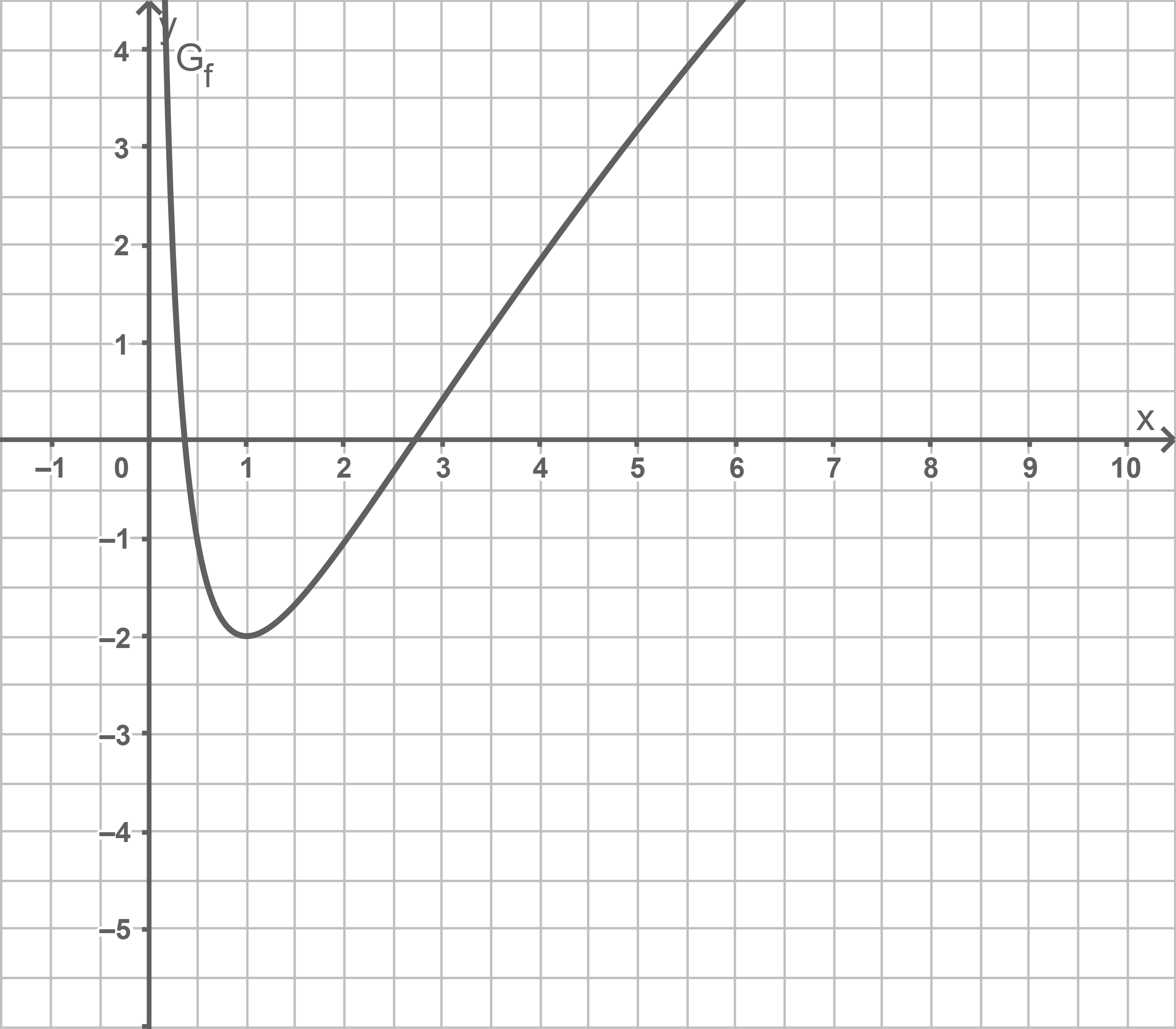
Gegeben ist die in  definierte Funktion
definierte Funktion  Abbildung 1 zeigt den Graphen
Abbildung 1 zeigt den Graphen  von
von 
 mit
mit  stellt in einem gewissen Bereich eine gute Näherung für
stellt in einem gewissen Bereich eine gute Näherung für  dar.
dar.

Abb. 1
1
a)
Zeige, dass  und
und  die einzigen Nullstellen von
die einzigen Nullstellen von  sind, und berechne die Koordinaten des Tiefpunkts
sind, und berechne die Koordinaten des Tiefpunkts  von
von 
(zur Kontrolle:  )
)
(5 BE)
b)
Zeige, dass  genau einen Wendepunkt
genau einen Wendepunkt  besitzt, und bestimme dessen Koordinaten sowie die Gleichung der Tangente an
besitzt, und bestimme dessen Koordinaten sowie die Gleichung der Tangente an  im Punkt
im Punkt 
(zur Kontrolle:  -Koordinate von
-Koordinate von  )
)
(6 BE)
c)
Begründe, dass  und
und  gilt. Gib
gilt. Gib  und
und  auf eine Dezimale genau an und zeichne den Graphen der Ableitungsfunktion
auf eine Dezimale genau an und zeichne den Graphen der Ableitungsfunktion  unter Berücksichtigung aller bisherigen Ergebnisse in Abbildung 1 ein.
unter Berücksichtigung aller bisherigen Ergebnisse in Abbildung 1 ein.
(6 BE)
d)
Begründe unter Zuhilfenahme von Abbildung 1, dass es zwei Werte ![\(c\in ]0;6]\)](https://www.schullv.de/resources/formulas/286245b3c837fd179b8488275ca74ae7e84441e367642767d5a9604bbe59735c_light.svg) gibt, für die gilt:
gibt, für die gilt: 
Die gebrochen-rationale Funktion
(3 BE)
e)
Gib die Gleichungen der beiden Asymptoten des Graphen von  an.
an.
(2 BE)
f)
Im IV. Quadranten schließt  zusammen mit der
zusammen mit der  -Achse und den Geraden mit den Gleichungen
-Achse und den Geraden mit den Gleichungen  und
und  ein Flächenstück ein, dessen Inhalt etwa
ein Flächenstück ein, dessen Inhalt etwa  beträgt. Ermittle die prozentuale Abweichung von diesem Wert, wenn bei der Berechnung des Flächeninhalts die Funktion
beträgt. Ermittle die prozentuale Abweichung von diesem Wert, wenn bei der Berechnung des Flächeninhalts die Funktion  als Näherung für die Funktion
als Näherung für die Funktion  verwendet wird.
verwendet wird.
(5 BE)
2
Durch Spiegelung von  an der Geraden
an der Geraden  entsteht der Graph einer in
entsteht der Graph einer in ![\(]-\infty;8[\)](https://www.schullv.de/resources/formulas/b2f9c70ab39e9a574da2048acde3ff00d5a353172b7ef99379af7d153e63795b_light.svg) definierten Funktion
definierten Funktion  Dieser Graph wird mit
Dieser Graph wird mit  bezeichnet.
bezeichnet.
a)
Zeichne  in Abbildung 1 ein.
in Abbildung 1 ein.
(2 BE)
b)
Die beschriebene Spiegelung von  an der Geraden
an der Geraden  kann durch eine Spiegelung von
kann durch eine Spiegelung von  an der
an der  -Achse mit einer anschließenden Verschiebung ersetzt werden. Beschreibe diese Verschiebung und gib
-Achse mit einer anschließenden Verschiebung ersetzt werden. Beschreibe diese Verschiebung und gib  an, sodass
an, sodass  für
für ![\(x\in\;]-\infty;8[\)](https://www.schullv.de/resources/formulas/661b01a93841d39e6c7b039d17694dc49dfd98ab4ef1a9a1243111d37ee7adb9_light.svg) gilt.
gilt.
(3 BE)
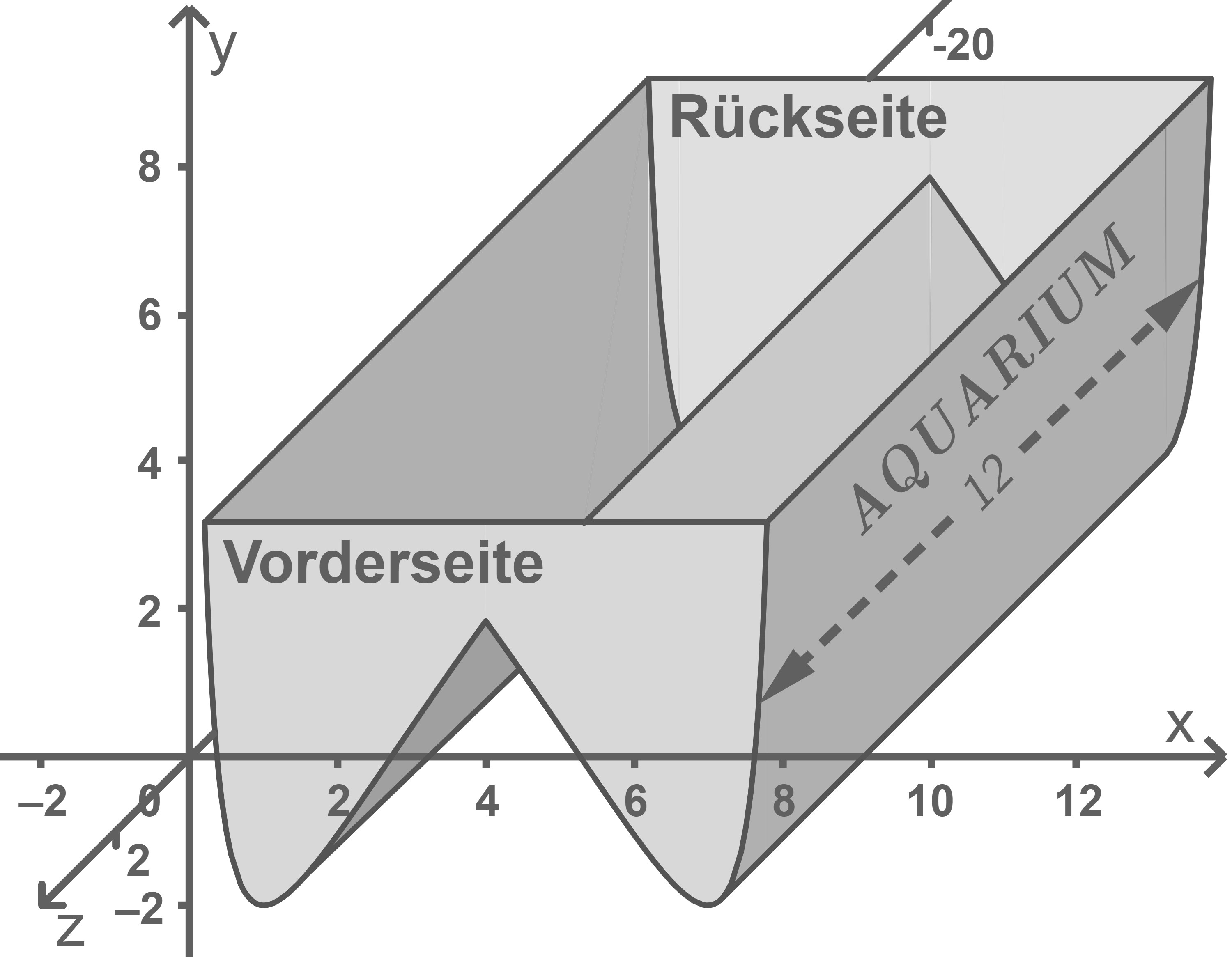
Im Folgenden wird die "w-förmige" Kurve  betrachtet, die sich aus dem auf
betrachtet, die sich aus dem auf  beschränkten Teil von
beschränkten Teil von  und dem auf
und dem auf  beschränkten Teil von
beschränkten Teil von  zusammensetzt. Die Kurve
zusammensetzt. Die Kurve  wird um 12 Einheiten in negative
wird um 12 Einheiten in negative  -Richtung verschoben. Die dabei überstrichene Fläche dient als Modell für ein 12 Meter langes Aquarium, das durch zwei ebene Wände an Vorderund Rückseite zu einem Becken ergänzt wird (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
-Richtung verschoben. Die dabei überstrichene Fläche dient als Modell für ein 12 Meter langes Aquarium, das durch zwei ebene Wände an Vorderund Rückseite zu einem Becken ergänzt wird (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.

Abb. 2
c)
Die Aquariumwände bilden an der Unterseite einen Tunnel, durch den die Besucher hindurchgehen können. Berechne die Größe des Winkels, den die linke und die rechte Tunnelwand miteinander einschließen.
Das Aquarium wird vollständig mit Wasser gefüllt.
(3 BE)
d)
Berechne die größtmögliche Wassertiefe des Aquariums.
(2 BE)
e)
Das Volumen des Wassers im Aquarium lässt sich analog zum Rauminhalt eines Prismas mit Grundfläche  und Höhe
und Höhe  berechnen. Erläutere, dass der Term
berechnen. Erläutere, dass der Term  das Wasservolumen im vollgefüllten Aquarium in Kubikmetern beschreibt.
das Wasservolumen im vollgefüllten Aquarium in Kubikmetern beschreibt.
(3 BE)
(40 BE)
1
a)
Nullstellen nachweisen
![\(\begin{array}[t]{rll}
f(x)&=& 0 \\[5pt]
2\cdot \left( \left(\ln x \right)^2-1 \right)&=& 0 &\quad \scriptsize \mid\; :2\\[5pt]
\left(\ln x \right)^2-1&=& 0 &\quad \scriptsize \mid\;+1 \\[5pt]
\left(\ln x \right)^2&=& 1 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
\ln x&=& \pm 1 \\[5pt]
x_1&=& \mathrm e \\[5pt]
x_2&=& \mathrm e^{- 1}
\end{array}\)](https://www.schullv.de/resources/formulas/7211084012d8a1fd24f180270f539c886890cfdbb0b454846d3169892c5907ab_light.svg) Die einzigen Nullstellen von
Die einzigen Nullstellen von  sind somit
sind somit  und
und  Koordinaten des Tiefpunkts berechnen
Für die ersten beiden Ableitungen von
Koordinaten des Tiefpunkts berechnen
Für die ersten beiden Ableitungen von  gilt:
gilt:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/e62f83fd16cf3dcbfa6525788479abb9656b812a4f878cbcc7cd5233b50ead30_light.svg) 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/ded0b09946eeef681cf7befe7f914b8b479225022555c7dcf49288b0da55a89f_light.svg) 2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/8587ce21108b59b9b64365bdf2a18b066456cb8a2f2ada0cae5b7a6763513b28_light.svg) Der Graph
Der Graph  besitzt somit bei
besitzt somit bei  den gesuchten Tiefpunkt. Einsetzen in
den gesuchten Tiefpunkt. Einsetzen in  liefert für die
liefert für die  -Koordinate:
-Koordinate:
![\(\begin{array}[t]{rll}
f(1)&=& 2\cdot \left( \left(\ln 1 \right)^2-1 \right) \\[5pt]
&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/ec1f846c1e70e01a2de16ecab4c3b787c9927145d147bcad9b3d18cfd536abdc_light.svg) Die Koordinaten des Tiefpunkts
Die Koordinaten des Tiefpunkts  von
von  lauten somit
lauten somit 
b)
Koordinaten des Wendepunkts bestimmen
Für die dritte Ableitung von  gilt:
1. Schritt: Notwendiges Kriterium für Wendestellen anwenden
gilt:
1. Schritt: Notwendiges Kriterium für Wendestellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/793ce6c851b4830108135cd11fd78631d84df24aca4ba29148d85c7f3505bb76_light.svg) 3. Schritt: Hinreichendes Kriterium für Wendestellen überprüfen
3. Schritt: Hinreichendes Kriterium für Wendestellen überprüfen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/79edcab07625da2674c18565af2a4caab167a6f045449f1ff458cc2944e77ada_light.svg) Bei
Bei  besitzt
besitzt  somit seinen einzigen Wendepunkt
somit seinen einzigen Wendepunkt 
Da eine Nullstelle von
eine Nullstelle von  ist, lauten die Koordinaten des Wendepunkts
ist, lauten die Koordinaten des Wendepunkts  Tangentengleichung bestimmen
Die Steigung
Tangentengleichung bestimmen
Die Steigung  der gesuchten Tangente enstpricht der Steigung von
der gesuchten Tangente enstpricht der Steigung von  im Punkt
im Punkt 
![\(\begin{array}[t]{rll}
m&=& f](https://www.schullv.de/resources/formulas/422ace4356838d3cf595d29279eaedc33decb045025320d244354ffdda47ab67_light.svg) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in
in  liefert für
liefert für 
![\(\begin{array}[t]{rll}
0 &=& \dfrac{4}{\mathrm e}\cdot \mathrm e +b \\[5pt]
0&=& 4 +b &\quad \scriptsize \mid\; -4 \\[5pt]
-4&=& b
\end{array}\)](https://www.schullv.de/resources/formulas/863b3e63e781c1ff47e0a1b289b74f274241ab3a0983945970a77eb3575f7191_light.svg) Eine Gleichung der Tangente
Eine Gleichung der Tangente  an
an  im Punkt
im Punkt  ist somit gegeben durch
ist somit gegeben durch 
Da
c)
Grenzwerte begründen
Für  gilt
gilt  Da im Nenner des anderen Faktoren ein
Da im Nenner des anderen Faktoren ein  steht, geht dieser gegen
steht, geht dieser gegen  Somit gilt insgesamt
Somit gilt insgesamt  Für
Für  gilt
gilt  Somit folgt:
Ableitungswerte bestimmen
Somit folgt:
Ableitungswerte bestimmen
![\(\begin{array}[t]{rll}
f‘(0,5)&=&\dfrac{4}{0,5}\cdot(\ln 0,5) \\[5pt]
&\approx& -5,5 \\[10pt]
f‘(10)&=& \dfrac{4}{10}\cdot(\ln 10) \\[5pt]
&\approx& 0,9
\end{array}\)](https://www.schullv.de/resources/formulas/88a6f8012d4472e1b851e8d4d9b43d4e6d93055d8580ccef068f936b07280998_light.svg) Graphen zeichnen
Graphen zeichnen
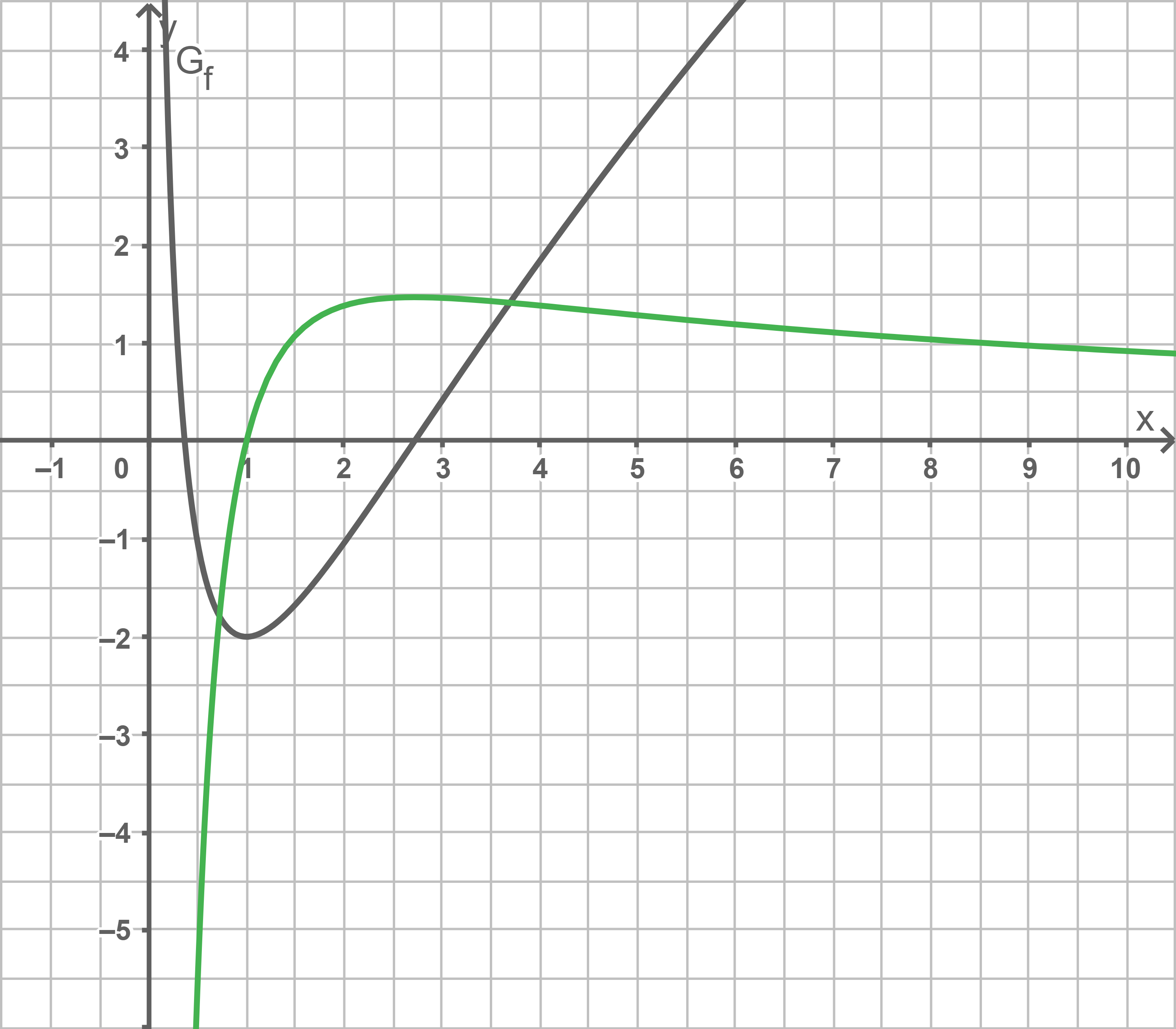

d)
Einer der beiden Werte ist  In dem Fall stimmen die obere und untere Integrationsgrenze überein, sodass das Integral den Wert Null hat.
In dem Fall stimmen die obere und untere Integrationsgrenze überein, sodass das Integral den Wert Null hat.
Aus Abbildung 1 wird deutlich, dass die von mit der
mit der  -Achse eingeschlossene Fläche zwischen
-Achse eingeschlossene Fläche zwischen  und
und  größer ist, als die zwischen
größer ist, als die zwischen  und
und  Somit existiert ein Wert
Somit existiert ein Wert  sodass der Inhalt der Flächen, die der Graph zwischen
sodass der Inhalt der Flächen, die der Graph zwischen  und
und  unterhalb und zwischen
unterhalb und zwischen  und
und  überhalb der
überhalb der  -Achse einschließt, gleich groß sind. Auch für diesen Wert
-Achse einschließt, gleich groß sind. Auch für diesen Wert  liefert das Integral somit den Wert Null.
liefert das Integral somit den Wert Null.
Aus Abbildung 1 wird deutlich, dass die von
e)
f)
Für den Inhalt der Fläche, die der Graph von  mit der
mit der  -Achse und den beiden Geraden zu
-Achse und den beiden Geraden zu  und
und  einschließt gilt:
Für die gesuchte prozentuale Abweichung folgt somit:
einschließt gilt:
Für die gesuchte prozentuale Abweichung folgt somit:
![\(\begin{array}[t]{rll}
\dfrac{1,623-1,557}{1,623}&\approx & 0,0407 \\[5pt]
&=& 4,07\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/60efa83daab436671df6415e5e3d413a4ce8626ad38bf24d15e83352923f7ace_light.svg)
2
a)
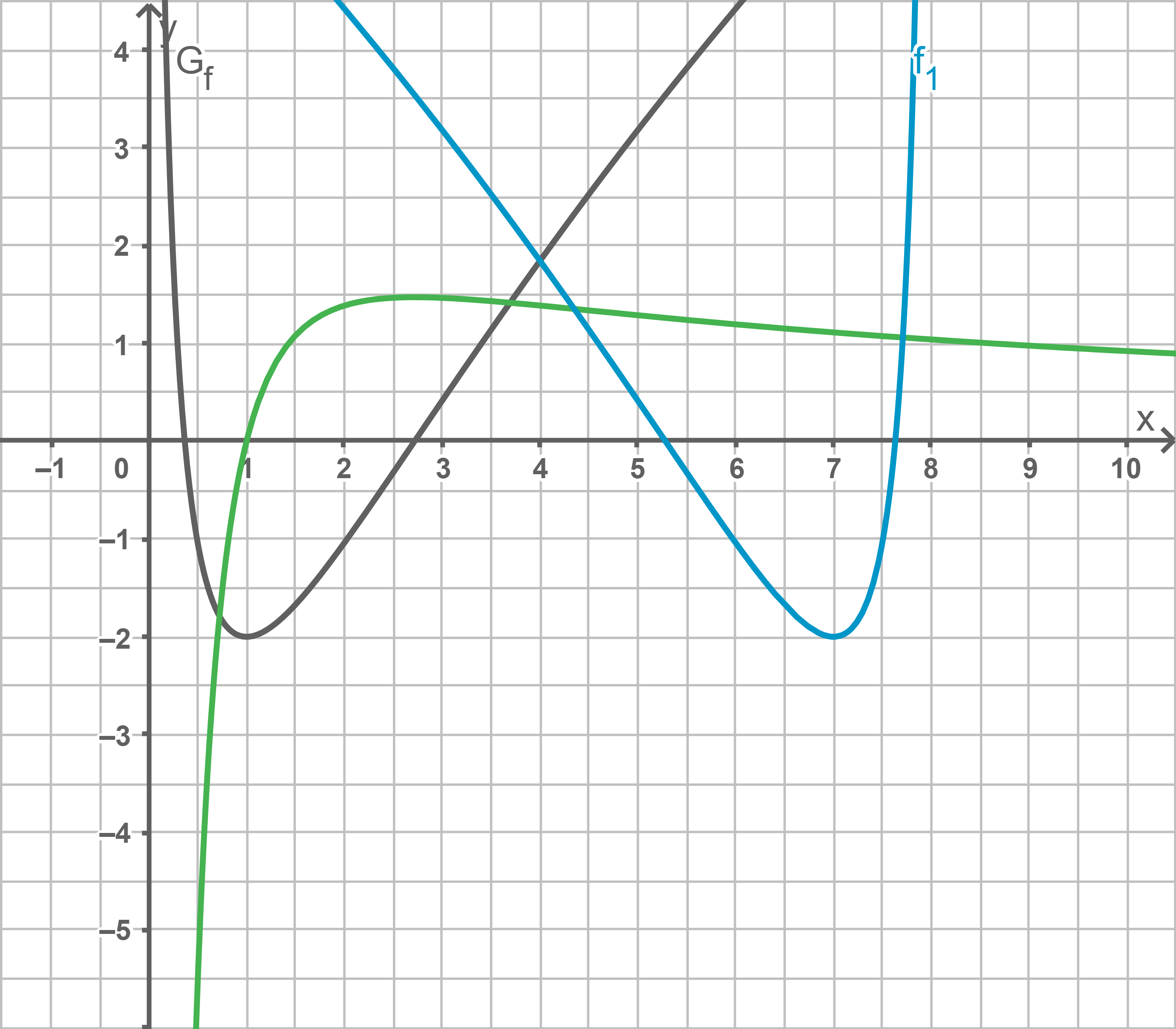
b)
Wird der Graph von  an der
an der  -Achse gespiegelt, ist die Spiegelachse
-Achse gespiegelt, ist die Spiegelachse  Für die zugehörige Funktion
Für die zugehörige Funktion  gilt dann
gilt dann  Bei der Spiegelung an
Bei der Spiegelung an  gilt allerdings
gilt allerdings  Somit muss der Graph nach der Spiegelung an der
Somit muss der Graph nach der Spiegelung an der  -Achse um acht Einheiten in positive
-Achse um acht Einheiten in positive  -Richtung verschoben werden.
-Richtung verschoben werden.
Es gilt Die anschließende Verschiebung liefert:
Die anschließende Verschiebung liefert:

 Somit gilt
Somit gilt  und
und 
Es gilt
c)
Der Winkel, den die beiden Tunnelwände miteinander einschließen, entspricht dem Winkel, den die Graphen von  und
und  an ihrer Schnittstelle
an ihrer Schnittstelle  miteinander einschließen. Für die Ableitung von
miteinander einschließen. Für die Ableitung von  folgt:
Für die Steigungen der Graphen von
folgt:
Für die Steigungen der Graphen von  und
und  an der Stelle
an der Stelle  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/ca070ad1b9d99c5a81855be96c8e39d8ca80a469468b1f7f60f1cc4ecff8b4a6_light.svg) Die Formel für den Schnittwinkel zweier Graphen liefert:
Die Formel für den Schnittwinkel zweier Graphen liefert:
![\(\begin{array}[t]{rll}
\tan (\alpha) &=& \dfrac{g](https://www.schullv.de/resources/formulas/c476dab2ccad1077110d78579ec23668522cd9ecaac2ecb246c52ac2bf35ddf2_light.svg) Die beiden Tunnelwände schließen somit einen Winkel der Größe ca.
Die beiden Tunnelwände schließen somit einen Winkel der Größe ca.  ein.
ein.
d)
Der tiefste Punkt des Wasserbeckens im Modell wird durch den Tiefpunkt von  bzw.
bzw.  beschrieben. Für die Höhe der Wasseroberfläche folgt:
beschrieben. Für die Höhe der Wasseroberfläche folgt:
![\(\begin{array}[t]{rll}
f(0,2)&=& 2\cdot \left(\left(\ln 0,2 \right)^2 -1\right) \\[5pt]
&\approx& 3,18 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/41a69cf47e37327130908d962bf9ff0b839b7718285ee86d5183fb821a961678_light.svg) Mit Hilfe der Koordinaten des Tiefpunkts von
Mit Hilfe der Koordinaten des Tiefpunkts von  aus Aufgabenteil 1a) folgt, dass die größtmögliche Wassertiefe
aus Aufgabenteil 1a) folgt, dass die größtmögliche Wassertiefe ![\(3,18- (-2) = 5,18\,[\text{m}]\)](https://www.schullv.de/resources/formulas/e58b262a4bdee10fba66cd6e9f22590712139eb0878054f6dc144234289e4b8c_light.svg) beträgt.
beträgt.
e)
Das Volumen eines Prismas wird durch  berechnet.In diesem Fall gilt
berechnet.In diesem Fall gilt  und
und  ist die Fläche, die die Kurve
ist die Fläche, die die Kurve  zusammen mit der Geraden
zusammen mit der Geraden  einschließt. Da die Fläche achsensymmetrisch zur Gerade
einschließt. Da die Fläche achsensymmetrisch zur Gerade  ist, genügt es den Flächeninhalt der linke Hälfte mit Hilfe eines Integrals über die Differenzenfunktion
ist, genügt es den Flächeninhalt der linke Hälfte mit Hilfe eines Integrals über die Differenzenfunktion  zu bestimmen und den erhaltenen Wert zu verdoppeln. Mit den Integrationsgrenzen
zu bestimmen und den erhaltenen Wert zu verdoppeln. Mit den Integrationsgrenzen  und
und  folgt somit für das Volumen:
folgt somit für das Volumen: