Teil B

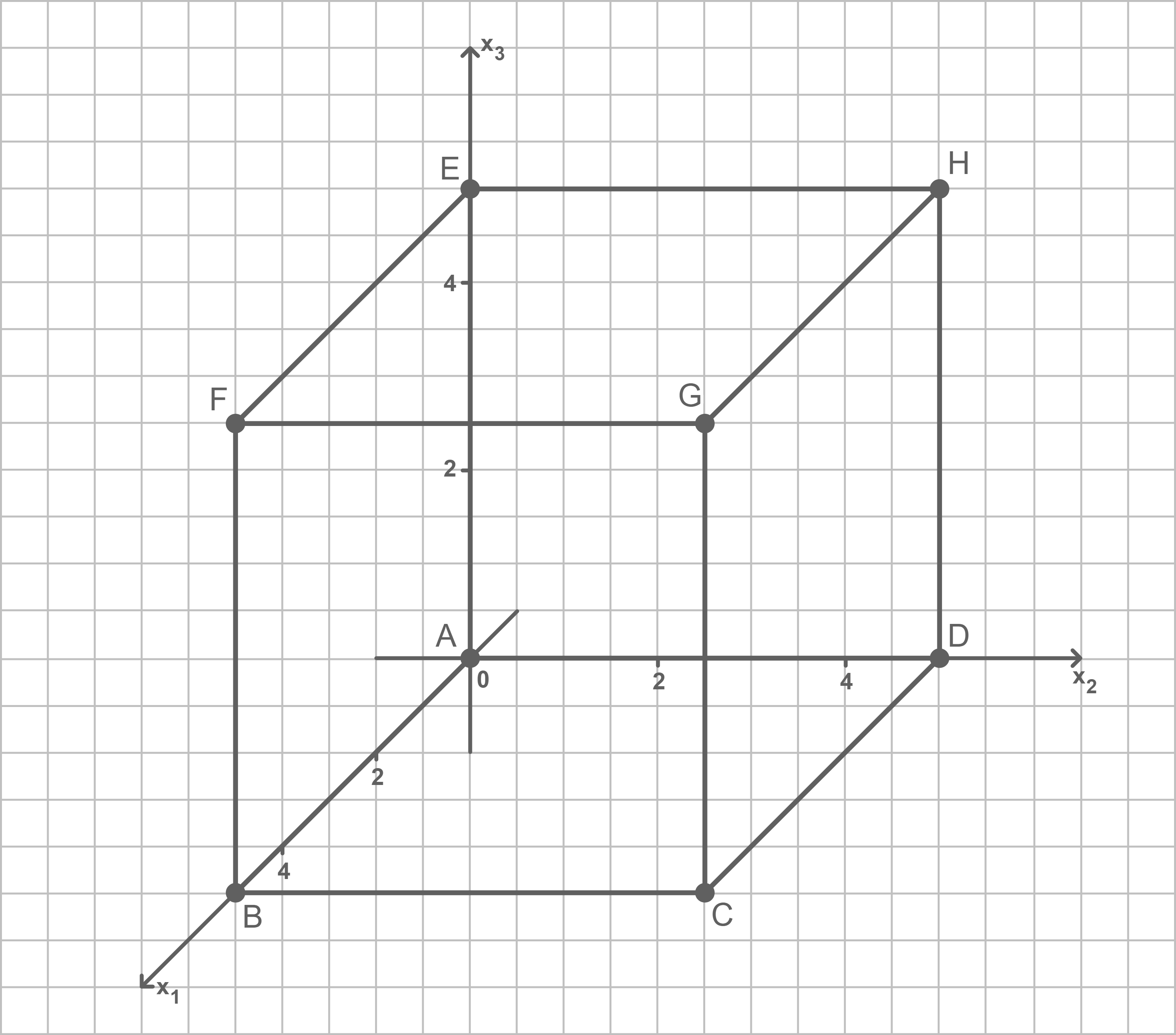
Die Abbildung zeigt den Würfel $ABCDEFGH$ mit $A(0\mid0\mid 0)$ und $G(5\mid5\mid 5)$ in einem kartesischen Koordinatensystem. Die Ebene $T$ schneidet die Kanten des Würfels unter anderem in den Punkten $I(5\mid0\mid 1),$ $J(2\mid5\mid 0),$ $K(0\mid5\mid 2)$ und $L(1\mid0\mid 5).$

Zeichne das Viereck $IJKL$ in die Abbildung ein und zeige, dass es sich um ein Trapez handelt, bei dem zwei gegenüberliegende Seiten gleich lang sind.

(4 BE)

Ermittle eine Gleichung der Ebene $T$ in Normalenform.

(zur Kontrolle: $T: \, 5x_1+4x_2+5x_3-30=0$ )

(3 BE)

Für $a\in\mathbb{R}^+$ ist die Gerade $g_a : \overrightarrow{x} = \pmatrix{2,5\\0\\3,5} + \lambda \cdot \pmatrix{0\\-10a\\\frac{2}{a}}$ mit $\lambda\in\mathbb{R}$ gegeben.

Bestimme den Wert von $a,$ sodass die Gerade $g_a$ die Würfelfläche $CDHG$ in ihrem Mittelpunkt schneidet.

(3 BE)

Für jedes $a\in\mathbb{R}^+$ liegt die Gerade $g_a$ in der Ebene $U$ mit der Gleichung $x_1=2,5.$

Ein beliebiger Punkt $P(p_1\mid p_2\mid p_3)$ des Raums wird an der Ebene $U$ gespiegelt. Gib die Koordinaten des Bildpunkts $\(P$ in Abhängigkeit von $p_1,p_2$ und $p_3$ an.

(2 BE)

Spiegelt man die Ebene $T$ an $U,$ so erhält man die von $T$ verschiedene Ebene $\(T$ Zeige, dass für einen bestimmten Wert von $a$ die Gerade $g_a$ in der Ebene $T$ liegt, und begründe, dass diese Gerade $g_a$ die Schnittgerade von $T$ und $\(T$ ist.

(4 BE)

Die Spitze einer Pyramide mit der Grundfläche $IJKL$ liegt auf der Kante $[FG]$ . Untersuche, ob die Höhe dieser Pyramide 2 betragen kann.

(4 BE)

(20 BE)

Viereck einzeichnen

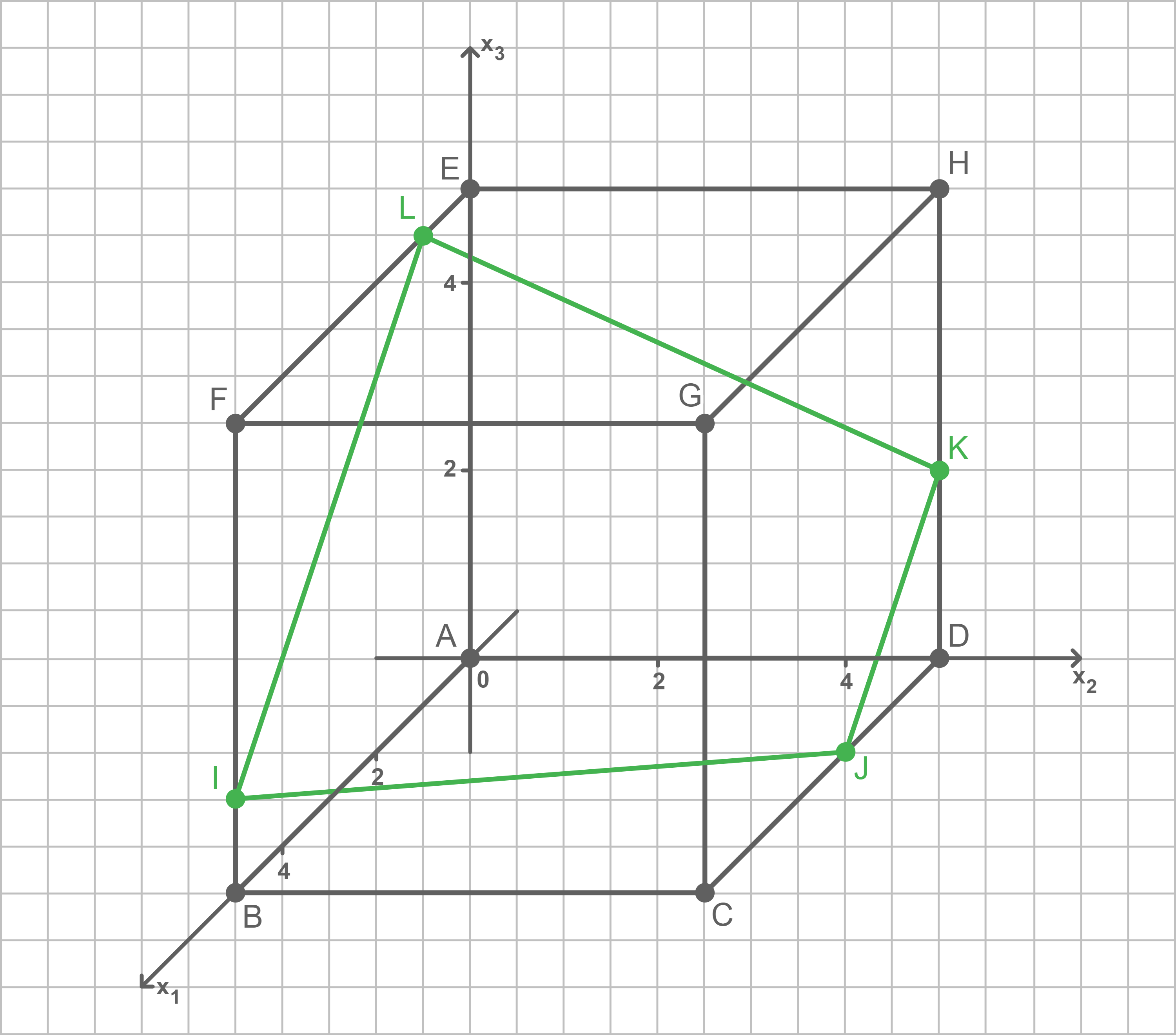Trapezform mit zwei gleich langen Seiten zeigen

Durch die Abbildung wird deutlich, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten $[LI]$ und $[KJ]$ sind. Für die zugehörigen Verbindungsvektoren folgt:

$\begin{array}[t]{rll} \overrightarrow{LI} &=& \pmatrix{4\\0\\-4} \\[5pt] \overrightarrow{KJ} &=& \pmatrix{2\\0\\-2} \end{array}$

Es gilt $\overrightarrow{LI} = 2\cdot \overrightarrow{KJ},$ das heißt die beiden Vektoren sind linear abhängig und somit parallel zueinander. Damit handelt es sich bei dem Viereck $IJKL$ um ein Trapez.

Für die Länge der anderen beiden Seiten $[LK]$ und $[IJ]$ folgt:

$\begin{array}[t]{rll} \overline{LK}&=& \left|\overrightarrow{LK} \right| \\[5pt] &=& \left|\pmatrix{-1\\5\\-3} \right| \\[5pt] &=& \sqrt{(-1)^2 + 5^2 + (-3)^2} \\[5pt] &=& \sqrt{35} \end{array}$

$\begin{array}[t]{rll} \overline{IJ}&=& \left|\overrightarrow{IJ} \right| \\[5pt] &=& \left|\pmatrix{-3\\5\\-1} \right| \\[5pt] &=& \sqrt{(-3)^2 + 5^2 + (-1)^2} \\[5pt] &=& \sqrt{35} \\[10pt] \end{array}$

Die beiden gegenüberliegenden Seiten $[LK]$ und $[IJ]$ sind somit gleich lang.

Mit dem Kreuzprodukt ergibt sich ein Normalenvektor der Ebene wie folgt:

$\begin{array}[t]{rll} \overrightarrow{n} &=& \overrightarrow{IJ}\times \overrightarrow{IK} \\[5pt] &=& \pmatrix{-3\\5\\-1}\times \pmatrix{-5\\5\\1} \\[5pt] &=& \pmatrix{ 5\cdot 1 - (-1)\cdot 5 \\ (-1)\cdot (-5) - (-3) \cdot 1 \\ (-3)\cdot 5 - 5\cdot (-5) } \\[5pt] &=& \pmatrix{10 \\ 8 \\ 10 } \\[5pt] &=& 2\cdot \pmatrix{5\\4\\5} \\[5pt] \end{array}$

Mit dem gekürzten Normalenvektor folgt:

$T: 5x_1 +4x_2 +5x_3 = d$

Einsetzen der Koordinaten z.B. des Punktes $L$ liefert für $d:$

$\begin{array}[t]{rll} T:5\cdot 1 +4\cdot 0 +5 \cdot 5 &=& d \\[5pt] 30&=& d \end{array}$

Eine mögliche Gleichung von $T$ in Normalenform lautet somit:

$T:5x_1+4x_2+5x_3-30=0$

Für den Ortsvektor des Mittelpunkts $M$ der Seitenfläche $CDHG$ folgt:

$\begin{array}[t]{rll} \overrightarrow{OM}&=&\dfrac{1}{2}\cdot\left(\overrightarrow{OD}+\overrightarrow{OG}\right) \\[5pt] &=&\dfrac{1}{2}\cdot\left(\pmatrix{0\\5\\0}+\pmatrix{5\\5\\5}\right) \\[5pt] &=&\pmatrix{2,5\\5\\2,5} \end{array}$

Gleichsetzen mit der Geradengleichung von $g_a$ liefert:

Rechenweg anzeigen

$\pmatrix{0\\5\\-1} = \lambda \cdot \pmatrix{0\\-10a \\ \frac{2}{a}}$

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 0 &=& \lambda \cdot 0 \\ \text{II}\quad& 5 &=& \lambda \cdot (-10a) \\ \text{III}\quad& -1 &=& \lambda \cdot \frac{2}{a} \\ \end{array}$

Aus der dritten Gleichung folgt:

$\begin{array}[t]{rll} -1 &=& \lambda \cdot \frac{2}{a} &\quad \scriptsize \mid\; \cdot a \\[5pt] -a &=& 2\lambda &\quad \scriptsize \mid\; \cdot (-1) \\[5pt] a &=& -2\lambda \\[5pt] \end{array}$

Einsetzen in $\text{II}$ liefert:

Rechenweg anzeigen

$\begin{array}[t]{rll} \lambda_1&=&-0,5 \\[5pt] \lambda_2&=&0,5 \end{array}$

Einsetzen in $a=-2\lambda$ liefert:

$\begin{array}[t]{rll} a_1 &=& -2\cdot (-0,5) \\[5pt] &=& 1 \end{array}$

$\begin{array}[t]{rll} a_2 &=& -2\cdot 0,5 \\[5pt] &=& -1 \end{array}$

Da $a\in \mathbb{R}^+$ gelten muss, ist $a_1$ die gesuchte Lösung. Für $a=1$ schneidet die Gerade $g_a$ die Würfelfläche $CDHG$ somit in ihrem Mittelpunkt.

Die Ebene $U$ mit $x_1 = 2,5$ verläuft parallel zur $x_2x_3$ -Ebene. Dadurch verändert sich durch die Spiegelung lediglich die $x_1$ -Koordinate.
Den Spiegelpunkt $\(P$ kann durch Spiegelung von $P$ an der $x_2x_3$ -Achse und anschließender Verschiebung um $2\cdot 2,5=5$ Längeneinheiten entlang der $x_1$ -Achse konstruiert werden.
Die Koordinaten des Spiegelpunkts ergeben sich somit als $\(P$

Lage der Gerade in der Ebene zeigen

Die Gerade $g_a$ liegt in der Ebene $T,$ wenn sie parallel zu $T$ verläuft und der Stützpunkt der Geraden in der Ebene liegt.

1. Schritt: Parallelität zeigen

Rechenweg anzeigen

$\begin{array}[t]{rll} a_1&=&0,5 \\[5pt] a_2&=&-0,5 \end{array}$

Da $a\in \mathbb{R}^+$ gelten muss, ist $a = 0,5$ der einzige Wert, für den die Gerade $g_a$ parallel zu $T$ verläuft.

2. Schritt: Lage des Stützpunktes zeigen

Einsetzen der Koordinaten des Stützpunktes von $g_a$ in die Ebenengleichung von $T$ liefert:

Rechenweg anzeigen

$0 = 0$

Der Punkt liegt also in der Ebene $T.$ Insgesamt liegt damit für $a=0,5$ die gesamte Gerade $g_a$ in der Ebene $T.$

Schnittgerade begründen

Der erste Eintrag des Richtungsvektors aller Geraden $g_a$ ist Null. Dadurch haben alle Punkte der Geraden $g_a$ die $x_1$ -Koordinate $2,5$ des Stützpunkts und $g_a$ liegt damit für jeden Wert von $a$ vollständig in der Ebene $U$ mit der Ebenengleichung $x_1 = 2,5.$
Für $a=0,5$ liegt $g_a$ also in $U$ und $T$ und ist die Schnittgerade von $T$ und $U.$ Da Punkte aus $U$ durch die Spiegelung auf sich selbst abgebildet werden, ist $g_a$ für $a=0,5$ somit die Schnittgerade von $T$ und $\(T$

Höhe der Pyramide überprüfen

Die Spitze liegt auf der Kante $[FG],$ die Teil der Geraden durch die beiden Punkte $F$ und $G$ mit folgender Geradengleichung ist:

$\begin{array}[t]{rll} FG:\overrightarrow{x} &=& \overrightarrow{OF} + t\cdot \overrightarrow{FG} \\[5pt] &=& \pmatrix{5\\0\\5} + t\cdot \pmatrix{0\\5\\0} \\[5pt] &=& \pmatrix{5\\5t\\5} \\[5pt] \end{array}$

1. Schritt: Punkt mit dem Abstand berechnen

Für die Hessesche Normalenform von $T$ folgt:

Rechenweg anzeigen

$T:\dfrac{5x_1 +4x_2 +5x_3 -30 }{ \sqrt{66}}=0$

Der Abstand eines Punkts $P(x_1\mid x_2\mid x_3)$ zu $T$ beträgt somit:

$d(P,T) = \dfrac{\left|5x_1 +4x_2 +5x_3 -30\right|}{ \sqrt{66}}$

Einsetzen der Koordinaten eines allgemeinen Punkts auf $FG$ und Gleichsetzen des Abstandes mit $2$ liefert:

Rechenweg anzeigen

$\left|20+20t \right| = 2\sqrt{66}$

Somit folgt:

Rechenweg anzeigen

$\begin{array}[t]{rll} t_1&\approx&-0,19 \\[5pt] t_2&\approx&-1,81 \end{array}$

2. Schritt: Lage auf der Kante überprüfen

Beide Werte von $t,$ die oben berechnet wurden, liegen nicht zwischen $0$ und $1,$ sodass die zugehörigen Punkte mit dem Abstand $2$ zu $T$ nicht auf der Kante $[FG]$ liegen.
Die Pyramide kann somit nicht die Höhe $2$ besitzen.